半亩方塘一鉴开 多维视角共徘徊——2023年全国数学高考乙卷理科第20题的解法探究与拓展

陈熙春, 李小刚

(六盘山高级中学,宁夏 银川 750002)

圆锥曲线中的定点、定值问题一直是高考中值得关注的问题.由于其形式多变,方法灵活,成了近几年高考的热点与难点之一.本文以2023年全国数学高考乙卷理科第20题的第2)小题为例,多角度探究求解,以期促进学生系统掌握解题方法,培养理性思维,并全面提升解题能力.

1 真题呈现

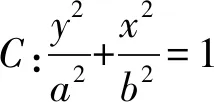
1)求C的方程;

2)过点(-2,3)的直线交C于点P,Q,直线AP,AQ与y轴的交点分别为点M,N,证明:线段MN的中点为定点.

(2023年全国数学高考乙卷理科试题第20题)

此题以椭圆为载体,背景是高等几何中的极点极线模型.以极点极线为背景的问题一直是高考中的“常青树”.试题新颖别致,立意高远而厚重,构思独具匠心,突出关键能力考查,素养要求高,重视考查学生的数学核心素养,体现了高考试题从能力立意到素养导向的功能.此题解法十分灵活,解题入口宽,深入难,区分度较高,凸显了高考试题的选拔性,是一道有丰厚内涵的经典试题[1].

2 多维视角,解法探究

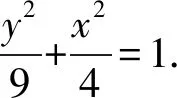
思维视角1联立方程,设而不求.

解法1(普通方程法)

由题意可知直线PQ的斜率存在.设P(x1,y1),Q(x2,y2),PQ:y=k(x+2)+3.联立方程

消去y,得

(4k2+9)x2+8k(2k+3)x+16(k2+3k)=0.

由Δ>0,解得k<0,可得

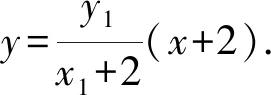
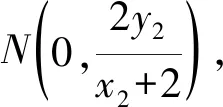
故线段MN的中点是定点(0,3).

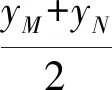
解法2(整体代换法)

设P(x1,y1),Q(x2,y2),B(-2,3),M(0,yM),N(0,yN),PQ:y=k(x+2)+3.联立方程

消去y,得

(4k2+9)(x+2)2+(24k-36)(x+2)+36=0.

由根与系数的关系可得

因为A(-2,0),所以直线

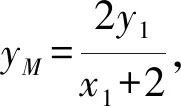
故线段MN的中点是定点(0,3).

评注利用整体的思想,构造出关于x+2的一元二次方程,得到斜率间的等量关系,把x+2看成整体以后,比解法1要简洁,运算量大大简化.这种整体代换的思想是处理解析几何烦琐运算的一种有效策略.

思维视角2构造齐次式.

解法3(构造和齐次化法)

9[(x+2)-2]2+4y2=36,

即

9(x+2)2-36(x+2)+4y2=0.

齐次化,得

9(x+2)2-36(x+2)[m(x+2)+ny]+4y2=0,

化简得

4y2-36ny(x+2)+(9-36m)(x+2)2=0.

等式两边同除以(x+2)2,构造斜率式,得

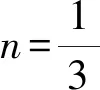
由根与系数的关系得kAQ+kAP=3.

由A(-2,0)可设直线AP的方程为

y=kAP(x+2).

令x=0,得

yM=2kAP,

同理可得

yN=2kAQ.

因此,线段MN的中点的纵坐标为

故线段MN的中点是定点(0,3).

解法4(平移变换和齐次化法)

将坐标系向左平移两个单位,即点A(-2,0)平移至原点A′(0,0),此时定点B(-2,3)变为B′(0,3).此时椭圆方程为

变形得 4y2+9x2-36x=0.

(1)

设平移后直线PQ的方程为mx+ny=1,且过点B′(0,3),从而

把直线PQ的方程mx+ny=1代入式(1),得

4y2+9x2-36x(mx+ny)=0,

整理得

4y2-36nxy+(9-36m)x2=0.

等式两边同除以x2,构造斜率式,得

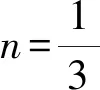
由根与系数的关系,得

kA′Q+kA′P=3,

由A′(0,0)可设直线A′P的方程为

y=kA′Px.

令x=2,得

yM=2kA′P.

同理可得

yN=2kA′Q.

因此,线段MN的中点的纵坐标为

故线段MN的中点是定点(0,3).

评注采用构造齐次化运算主要解决直线与圆锥曲线中斜率之和或斜率之积为定值的问题．这个定的问题最后转化成了斜率之和或斜率之积为定值的证明.齐次化运算比传统的设而不求极大地简化了计算量,其核心就是先构造斜率的二次方程,再利用根与系数的关系求解.

思维视角3点差法.

解法5(点差法和三点共线)

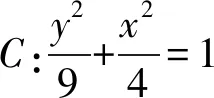
即

同理可得

两式相减,得

(2)

又知点B,P,Q共线可得

变形可得

即

k1+k2=3,

故线段MN的中点是定点(0,3).

评注利用“点差法”,通过设点、代点、作差构造出kAP,kAQ的表达式,便可轻松解决.

解法6(点差法和斜率双用)

设点B(-2,3),P(x1,y1),Q(x2,y2),直线AP,AQ的斜率分别为k1,k2,易得MN的中点坐标为(0,k1+k2).由

两式相减,得

同理可得

不妨设k1+k2=m,则

化简可得

4y1y2-9x1x2+18x1-18x2+36=4my2x1+8my2,

同理可得

4y1y2-9x1x2+18x2-18x1+36=4my1x2+8my1,

两式相减,得

9(x1-x2)=m(y2x1-y1x2)+2m(y2-y1).

(3)

又由点B,P,Q共线,得

化简可得

9(x1-x2)=3(y2x1-y1x2)+6(y2-y1),

(4)

将式(3)与式(4)对比,可得m=3,故线段MN的中点是定点(0,3).

评注此题为“斜率和”问题.在解题中涉及斜率和的问题时的解题规律:写出原式→交叉使用→化整作差→对照两点式.这种方法同样可以解决“斜率积”问题.

思维视角4借梯登高思维.

解法7(参数方程法)

设直线PQ的参数方程为

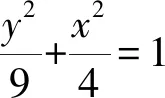
(4+5cos2α)t2+12(2sinα-3cosα)t+36=0.

设P,Q对应的参数分别为t1,t2,则

又P(-2+t1cosα,3+t1sinα),Q(-2+t2cosα,3+t2sinα),直线AP的方程为

令x=0,得

同理可得

因此线段MN的中点的纵坐标为

故线段MN的中点是定点(0,3).

评注充分利用直线分别与椭圆相交这一几何条件,利用参数方程实现了几何问题代数化,体现了解析几何的基本思想——数形结合,有效地减少了运算量.应用参数方程法是破解此类问题的一种有效策略.

解法8(三角代换法)

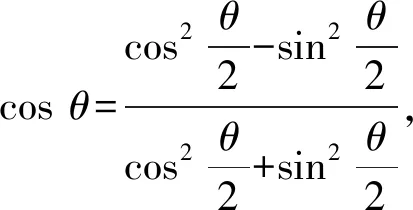
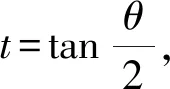
于是设椭圆的参数方程为

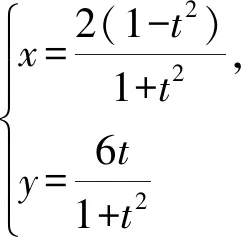
设B(-2,3),点P,Q对应的参数分别为t1,t2,由点B,P,Q共线,得

化简得

t1+t2=2.

又

同理可得

从而

由A(-2,0)可设直线AP的方程为

y=kAP(x+2).

令x=0,得

yM=2kAP,

同理可得

yN=2kAQ.

因此线段MN的中点的纵坐标为

故线段MN的中点是定点(0,3).

评注引入椭圆的参数方程,巧妙地实现了几何问题与三角函数的精彩联袂,使解题方向更加清晰明了.

解法9(定比插参法)

设点B(-2,3),P(x1,y1),Q(x2,y2),直线AP,AQ的斜率分别为k1,k2,易得MN的中点坐标为(0,k1+k2).因为点B,P,Q共线,所以

即

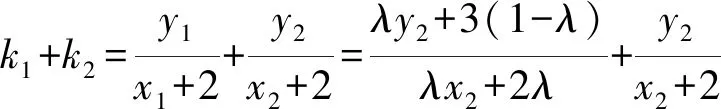
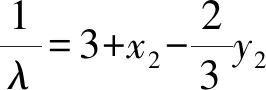
故线段MN的中点是定点(0,3).

评注解决此题的难点在于如何“设参”,焦点在于如何“用参”,重点在于如何“消参”.“设参—用参—消参”是解圆锥曲线问题的基本方法.因此定值问题的解题思路是:1)设参数;2)用参数来表示要求定值的式子;3)消参数.

思维视角5利用曲线系方程.

解法10(曲线系法)

设直线AP:x=m1y-2,AQ:x=m2y-2,PQ:y=kx+b,设直线AP,AQ的斜率分别为k1,k2,易得MN的中点坐标为(0,k1+k2).由直线PQ过点(-2,3),知3=b-2k.又点P,Q在椭圆上,故可设过点A,P,Q的椭圆方程为

(x-m1y+2)(x-m2y+2)+λ(x+2)(y-kx-b)=0,

变形可得

(1-kλ)x2+m1m2y2+(λ-m1-m2)xy+2(λ-m1-m2)y+(4-bλ-2kλ)x+4-2bλ=0.

与椭圆C:9x2+4y2=36比较系数,得

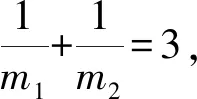
评注一般地,高考中出现的二次曲线为两对直线与一圆锥曲线组成的体系,通过添加系数,可以用其中的任意两个元素来表示第三个元素,从而建立等式,列出方程求解.利用曲线系方程,实际上把计算难度转移到直线方程系数的比较上,调整两个多项式恒等,其对应系数相等.

思维视角6同构法.

解法11设直线AP:x=m1y-2,AQ:x=m2y-2,PQ:x=m0y+n,则联立直线AP,PQ,可得

代入椭圆方程,得

同理可得

从而m1,m2为方程

(9n2-36)m2+(72m0+36m0n)m+4(2+n)2=0

(5)

的两个根.

由直线PQ过点(-2,3),得

n=-2-3m0,

代入式(5),得

设直线AP,AQ的斜率分别为k1,k2,从而MN的中点坐标为(0,k1+k2),于是

故MN的中点是定点(0,3).

评注同构是一种常见的思想方法,是映衬着数学的对称和谐之美的数学方法,是“同理可得”的理论基础,是函数与方程思想的代名词与具体体现.在解题中灵活利用同构式,可以起到化繁为简、“四两拨千斤”的作用.

(4k2+9)x2+16k2x+16k2-36=0.

当Δ>0时,由根与系数的关系,得

又xA=-2,从而

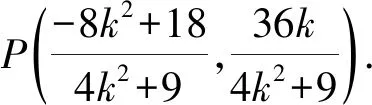
设直线PQ:y=m(x+2)+3,将点P的坐标代入,化简得

12k2-36k+36m+27=0.

同理可设直线AQ的斜率为k1,得

因此,k,k1是二次方程12x2-36x+36m+27=0的两个根,故k+k1=3.下同解法3(略).

评注利用同构思想解题相当于寻找斜率满足的二次方程,可以取得事半功倍的效果．在此题中方程有一个根是-2,利用根与系数的关系求出另一个根,可以减少计算量.

思维视角7营造对称,方便计算.

解法13(对偶式法)

设点B(-2,3),P(x1-2,y1),Q(x2-2,y2),因为点B,P,Q共线,所以

变形,得

y1x2-y2x1=3(x2-x1).

构造对偶式

因为直线AP的方程为

令x=0,得

同理可得

因此,线段MN的中点的纵坐标为

故线段MN的中点是定点(0,3).

评注构造对偶式重在“构造”,在运用时要对已知等式进行整体观察,利用代数式的对称性,设法构造有利于计算的代数式,简捷获解.对偶式主要是用于化简、转化定点、定直线的坐标表示,构造对偶式法在解题中具有广泛性、灵活性和简洁性的优势.

思维视角8高等数学视角.

解法14(调和点列法)

图1

2)调和线束的性质:若直线l∥MP,且与其他3条线分别交于点C,D,E,则D为CE的中点.

评注近年来,许多数学高考试题以极点、极线为背景进行命题.熟练使用极点、极线的结论,解题方向会更加清晰.以上相关的知识点在高考答题中不能直接使用,在应用时可以先利用调和线束的性质“猜测”结果,然后再用一般的方法进行证明或验证.极点、极线知识在解题中具有较强的优越性,有利于学生“居高临下”地站在系统的高度迅速地思考和解决问题,达到“会当凌绝顶,一览众山小”的功能,收到缩短思维长度、提高解题速度、节约解题时间的作用.

2 探究与拓展

限于篇幅,探究1～3的证明略.由此可见,例1是探究1结论的特殊情况.

3 往年高考试题链接

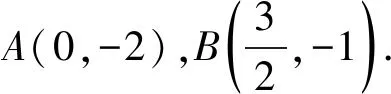
1)求E的方程;

(2022年全国数学高考乙卷理科试题第20题)

不难发现,2023年全国数学高考乙卷理科第20题的第2)小题与2022年全国数学高考乙卷理科第20题极其相似,可以看作“姊妹题”.两道题具有以下的共同特点:1)过椭圆外一点作直线与椭圆相交;2)线段的中点;3)极点、极线背景;4)方程相似,都为焦点在y轴上的椭圆;5)图形(模型)相似;6)解题思路相同.

4 解题感悟

圆锥曲线中的定值、定点问题淋漓尽致地体现了“几何”与“代数”的深度融合、“动态”与“静态”的完美和谐统一.定点、定值问题是探求“变中有不变的量”.因此,要注意挖掘问题中各个量之间的相互关系,恰当适时地运用函数与方程、转化与化归、数形结合、分类讨论、特殊到一般、相关点法、设而不求、换元、消元等基本思想方法.

此类问题综合性强,方法灵活.在解题过程中,既有探索性的历程,又有严密的逻辑推理及复杂的运算,成为考查学生数学核心素养的一道亮丽的风景线.文中的14种解法,各有千秋,笔者从深度和广度上进行了系统性探究、整合、推广,实现了从“一道题”到“一类题”质的飞跃,进而提升学生的核心素养,真可谓“半亩方塘一鉴开,多维视角共徘徊”!