挖掘向量数量积问题的破解策略

许 芳

(安徽省宣城市宣城中学)

数量积是平面向量重要的运算关系,在高中数学中有着广泛的应用.例如,利用两个向量的数量积运算可以推导两角和、差的三角公式,证明余弦定理,也可用于判断两条直线的位置关系以及求它们的夹角等.向量数量积的求解方法多种多样,本文介绍几种常用的方法,供同学们参考.

1 定义法

向量数量积的定义:a•b＝|a|•|b|cos‹a,b›,其中‹a,b›为向量a,b的夹角,范围是[0,π].定义法是求向量数量积最基本的方法.两个向量的夹角是两个向量共起点时所夹的角,在解答本题时,易将角B视为,,从而造成错解.

2 坐标法

运用坐标法求向量的数量积需结合题目条件建立相应的平面直角坐标系,表示出相应的向量,再利用向量的坐标运算求解,即

A.(0,8] B.[0,8)

C.(0,4] D.[0,4)

取正方形ABCD的边AB的中点为坐标原点建立如图1所示的平面直角坐标系,则A(－1,0),B(1,0),C(1,2),D(－1,2).

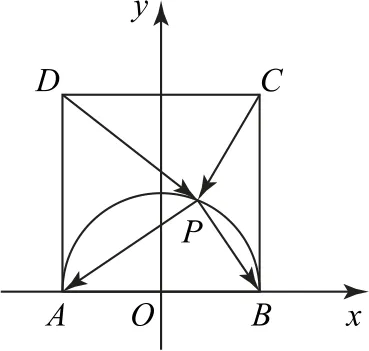
图1

图2

本题中的点P为动点,若直接利用向量的几何运算处理,较为烦琐,故考虑通过建立平面直角坐标系,利用坐标法求解.

3 特殊化法

在以平面几何为背景的向量数量积问题中,若题目条件中没有指明几何图形的具体形状,且所求的向量数量积为定值,则可将几何图形特殊化,从而利用特殊图形的性质简洁解题.

例3 若圆M为△ABC的外接圆,AB＝4,AC＝6,N为边BC的中点,则＝( ).

A.5 B.10 C.13 D.26

4 基底法

将平面内一组不共线的向量视为基底,可以用其表示平面内任意一个向量.在求解两个向量的数量积时,若这两个向量的模或夹角均不易求解时,可考虑用已知向量或特殊向量作为基底来表示未知向量,从而将未知化为已知.

例4 已知等边△ABC的边长为2,D为边BC的中点,点M是AC边上的动点,则的最大值为_______,最小值为______.

又D为BC的中点,所以

故

则

本题中的点D为动点,因此向量的模与夹角均不确定,直接求解较为困难,因此可采用基底法将其转化为已知向量或特殊向量的运算来完成,由于三角形的三边及夹角均已知,故可将其(或与其相关的向量)作为基底来表示未知向量.

5 投影法

将a•b＝|a|•|b|cos‹a,b›中的|b|cos‹a,b›视为一个整体,其意义为向量b在向量a上的投影.也可将|a|cos‹a,b›视为一个整体,即a在b上的投影.因此两个向量的数量积可以视为一个向量的模与另一个向量在该向量上投影的乘积.

易知a•e＝|a|•|e|cos‹a,e›＝|a|•cos‹a,e›,|a|•cos‹a,e›为向量a在向量上e的投影.

当a•e≤1时,向量a在向量上e的投影为1,如图3所示,此时|a|可以趋近于正无穷.

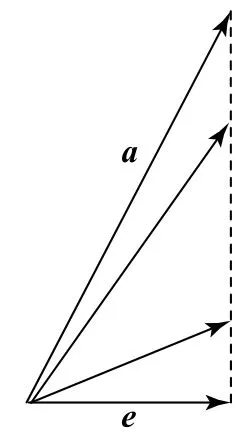
图3

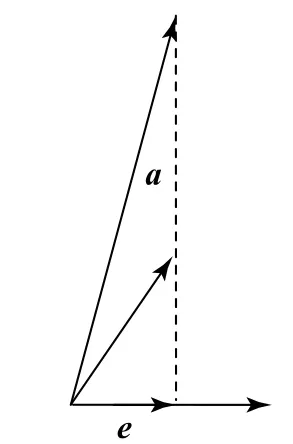
图4

本题所给条件为两个向量数量积的取值范围,且夹角不确定,故可利用投影法处理.向量的投影为实数,既可以是正值,也可以是负值,还可以是0,其正负情况与cos‹a,b›相同.

综上,对于一道向量数量积问题,我们可以从多个角度入手,运用多种方法解答,但解题时不能随意选择一种方法,需要仔细审视、挖掘题目条件信息,选择较为简单的方法.

(完)