例析与向量有关的最值、取值范围问题

郭 清 王 菲

(山东省淄博市桓台县渔洋中学)

与向量有关的最值、取值范围问题是向量中的重点题型,高考常考,求解策略常有以下几种.

1 利用一次函数的性质

例1 如图1 所示,在矩形ABCD中,AB＝2BC＝2,AC与BD的交点为M,N为边AB上任意点(包含端点),则的最大值为_________.

图1

以点A为坐标原点,的方向分别为x轴、y轴 正 方 向 建 立 如 图2所示的平面直角坐标系,则B(2,0),D(0,1),M(1,).

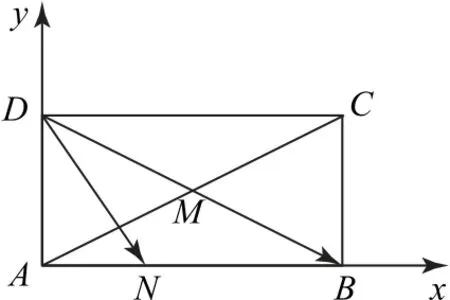
图2

对于一次函数f(x)＝ax＋b(a≠0),当a＞0时,f(x)在R 上单调递增;当a＜0 时,f(x)在R上单调递减.

2 利用二次函数的性质

作DO⊥AB于点O,以点O为原点,OB,OD所在直线 分 别 为x轴、y轴 建立如图3所示的平面直角坐标系.因为

图3

图4

3 利用a,b∈R∗,则a＋b≥2 ab

例3 若平面向量a,b满足|a|＝3|b|,且|ab|＝4,则a与a－b夹角的正弦值最大值为( ).

设|b|＝m,则|a|＝3m,因此

对于正数x,y,若xy为定值p,则当且仅当x＝y时,x＋y有最小值是2.若x＋y为定值s,则当且仅当x＝y时,xy有最大值是.

4 利用三角函数的性质

例4 已知边长为1的正方形ABCD位于第一象限,且顶点A,D分别在x轴和y轴的正半轴上(含原点O)滑动,则的最大值是( ).

当A与O重合时,B(1,0),C(1,1),此时,有

当A与O不重合时,如图5所示,设∠OAD＝θ(0≤θ＜),则

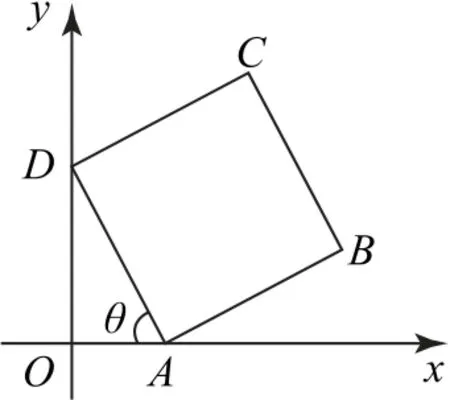
图5

图6

5 利用共线向量

当向量a,b的方向相同时,其夹角为0°;当向量a,b的方向相反时,其夹角为180°.

(完)