地震作用下高速铁路车-线-桥耦合系统动力响应分析

马理超, 王相平, 王戊寅, 张 旭, 李 强, 李国芳

(1. 兰州交通大学 机电工程学院, 甘肃 兰州 730070;2. 中国铁路兰州局集团有限公司 嘉峪关机务段, 甘肃 嘉峪关 735100)

0 引言

我国地震发生频率高、范围广[1-2]。在地震高发区,如果高速列车在桥上运行时突遇地震,轮轨间的接触状态、振动特性将受到影响。在整个车辆-轨道-桥梁耦合系统中,这不仅会影响车辆的动力学性能,还会对轨下结构造成异常的振动与冲击。基于此,研究地震作用下高速列车的车-线-桥耦合系统的动力响应对于高速铁路安全运营有着重要的意义。

随着“以桥带路”的建设理念被广泛应用,基于大系统研究车-线-桥耦合振动成为热点。翟婉明等[3]系统地建立了考虑多种非线性因素的列车-轨道-桥梁耦合模型。Yau[4]基于增量迭代法分析了地面沉降对车-线-桥耦合系统振动特性的影响,研究表明:列车垂向响应对地面沉降的变化非常敏感,桥梁结构对地面沉降的敏感性较弱。对于地震作用下高速列车运行安全性研究,高盟等[5]将DLOAD子程序与ABAQUS有限元计算程序联立,研究了地震载荷与移动载荷耦合作用下高速铁路路基的振动响应。刘冉冉[6]基于ANSYS建立了列车-桥耦合振动分析模型,研究了地震载荷和列车载荷同时作用时桥梁的动力响应。郭恩栋等[7]基于动力平衡方程研究了地震峰值加速度和列车运行速度对列车走行性三项指标的影响规律。国巍等[8]基于Simpack和OpenSees编制了车辆-轨道-桥梁系统联合仿真程序,对比分析了地震强度与列车运行速度对车辆运行安全指标的影响,结果表明:列车运行安全评价指标对地震强度与列车运行速度的变化较为敏感,影响轮重减载率的主要因素是列车运行速度。雷虎军等[9]发现采用传统的列车走行性三项指标评判地震作用下桥上列车服役安全性过于保守,认为车轮抬升量更适合作为地震作用下桥上列车行车安全性的评判依据。魏峰等[10]基于车辆-轨道-桥梁振动台台阵缩尺模型试验研究了地震作用下列车脱轨问题,并依据行车安全性及舒适度指标提出了不同地震强度等级下列车运行速度的安全限值。李昊等[11-12]建立了车辆-轨道动力学数值模型,研究了地震作用下高速铁路运行安全和脱轨机理,并利用随机振动原理给出了高速铁路地震预警阈值评价表。

综上可知,关于耦合系统的建模方法,学者们更多地采用有限元方法和数值方法,很少采用有限元-多体系统动力学(Finite Element-Multi-Body Dynamics,FE-MBD)方法建模,而FE-MBD方法可在保证计算精度的前提下大幅提高计算效率。有关地震作用下高速列车运行安全性的研究集中在列车走行性三项指标与轮轨接触几何指标方面,极少关注地震激励对车辆动力学性能和轨下结构振动特性的影响,而车辆动力学性能和轨下结构的振动特性对高速铁路安全运营有显著影响。鉴于此,本文采用FE-MBD方法建立高速铁路桥梁区段车辆-轨道-桥梁耦合系统动力学模型,基于《建筑抗震设计规范》[13]设计地震反应谱,分析地震作用下高速铁路车-线-桥耦合系统动力响应,揭示地震激励对车辆-轨道-桥梁耦合系统的振动特性的影响规律,为地震激励作用下高速铁路安全运营提供理论依据。

1 计算模型

1.1 车辆-轨道-桥梁耦合模型

高速铁路桥梁区段车辆-轨道-桥梁耦合系统动力学模型由车辆子系统、CRTSⅡ型板式无砟轨道子系统和桥梁子系统组成。设计线路总长150 m,桥梁长度32 m。桥梁结构和CRTSII型板式无砟轨道结构的材料均采用线弹性本构关系。

(1) 桥梁模型

桥梁模型采用标准32 m双线混凝土简支箱梁桥,混凝土等级为C50,桥梁结构采用Solid185单元模拟,可以充分体现桥梁结构任意位置的应变特点与振动特性。桥梁主箱梁实际尺寸和有限元模型如图1所示,其相关计算参数如表1所列。

表1 箱梁计算参数

图1 桥梁模型Fig.1 Bridge model

(2) 车辆模型

车辆模型采用CRH3型高速动车组,车轮踏面采用S1002CN,列车的主要参数如表2所列。多刚体车辆模型主要包括1个车体、2个构架、4个轮对、8个轴箱,考虑车体、构架、轮对具有6个自由度,轴箱具有1个自由度,共计50个自由度。

表2 车辆主要参数

(3) 轨道模型

轨道为CRTSⅡ型板式无砟轨道,轨道模型采用实体单元Solid185模拟轨道板和支撑层。由于砂浆层长度、宽度远大于厚度,且轨道结构建模的精细化程度并不会对CA砂浆层、扣件等构件的易损性产生影响,故不进行实体建模。采用弹簧-阻尼单元模拟CA砂浆层,基于多体动力学软件UM将CA砂浆层等效为Bushing力元,依据表3数据和式(1)和式(2)可计算出CA砂浆层的等效刚度和等效阻尼[14]。CRTSⅡ型板式轨道的计算参数如表3所列。

CA砂浆层的等效刚度计算方法如下:

(1)

式中:KCA_eq为CA砂浆层的等效刚度;ECA为砂浆层弹性模量;SCA为砂浆层面积;N为Bushing力元总数;hCA为砂浆层厚度。

等效阻尼CCA_eq采用Rayleigh阻尼,其计算方法如下:

(2)

式中:CCA_eq为CA砂浆层的等效阻尼;Mca、Kca为CA砂浆层对应的质量、刚度矩阵;ωi、ωj为结构固有频率;ξ为阻尼比,此处取0.025。

(4) 车辆-轨道-桥梁耦合模型

车辆-轨道-桥梁是一个相互作用的动态耦合系统,车辆运行时会对桥梁结构产生冲击从而引起桥梁的振动;而桥梁结构的振动反过来作用在车辆上,改变车辆的受力情况和运动状态,从而影响车辆的安全性和舒适性[15]。在王相平等[16]前期研究基础上,结合有限元软件ANSYS和多体动力学软件UM建立车辆子系统、CRTSⅡ型板式无砟轨道子系统和桥梁子系统;基于列车-轨道-桥梁相互作用关系建立高速铁路桥梁区段车辆-轨道-桥梁耦合系统动力学模型。钢轨以Timoshenko梁模拟,钢轨与轨道板之间由扣件连接,扣件以三向非线性弹簧模拟。轮轨接触模型采用Kik-Piotrowski[17-18]模型,板式轨道层间相互作用以非线性共节点力元模拟,轨道-桥梁之间以线桥相互作用[3]模拟,耦合系统动力学建模流程如图2(b)所示。

1.2 地震激励模型

即使在同一地点发生相同烈度的地震,记录到前后两次的地震加速度时程也会不同。根据不同的地震加速度时程可以设计不同的加速度反应谱,因此选择合理的地震加速度时程是进行桥梁结构地震响应分析的重要步骤。基于《建筑抗震设计规范》中地震影响系数曲线设计地震反应谱[19-20],采用谱分析方法对桥梁结构进行地震响应分析,根据轨道自身不平顺和谱分析得到桥梁结构的位移响应,计算得到整个轨道在地震作用下的位移响应,在多体动力学软件UM中以轨道不平顺的方式完成地震激励在耦合模型中的施加。

《建筑抗震设计规范》规定建筑物受地震影响的曲线如图3所示,该曲线是根据强震作用下在同一类场地上得到的地面加速度反应时程,分别计算其相应的反应谱曲线,然后通过统计分析得到的最具有代表性的平均反应谱曲线。地震影响系数相关计算参数的选取方式如下文所示。

图3 地震影响系数曲线Fig.3 Seismic influence coefficient curve

阻尼修正参数和形状参数的大小满足:

(1) 除了特殊规定外,建筑物的阻尼比大小应取0.05,地震影响系数曲线的修正阻尼大小应取1.0,形状因子的大小应符合下列规定:

① 当周期处于小于或等于0.1 s的区段时,曲线呈直线上升状态;

② 当周期处于0.1 s到一倍特征周期(Tg)的区段时,曲线呈水平状态,其值大小保持不变,应取最大值αmax;

③ 当周期处于一倍特征周期(Tg)到五倍特征周期(5Tg)的区段时,曲线呈非线性下降状态,衰减指数为0.9;

④ 当周期处于五倍特征周期(5Tg)到6 s的区段内,曲线呈直线下降状态,下降斜率调整系数为0.02。

图中α为地震影响系数;η1为直线段的下降斜率调整系数;η2为阻尼调整系数;αmax为地震影响系数的最大值;T为建筑物的结构自振周期;γ为衰减指数。

(2) 当指定建筑结构的阻尼比大小不等于0.05时:

① 阻尼修正因子:

(3)

式中:η2为阻尼修正因子;ξ为阻尼比。

② 衰减指数(曲线下降段处):

(4)

式中:γ为衰减指数。

③下降斜率修正因子(直线下降段处):

(5)

式中:η1为直线段的下降斜率修正因子。

(3) 设计特征周期Tg与地震影响系数的最大值αmax的取值如表4和表5所列。

表4 设计特征周期值Tg(单位:s)

表5 水平地震影响系数最大值αmax

1.3 模型验证

由于目前缺乏地震激励下车辆-轨道-桥梁耦合系统动力特性相关的监测数据,为验证模型的准确性,在文献[16]模型验证基础上,将文中模型的计算结果与文献[3]中的计算结果进行对比。文中模型计算得到的轮轴横向力变化曲线如图4所示,与文献[3]中的计算值和测试值对比,由图可知计算结果误差较小,可知其能够满足计算需求。

图4 轮轴横向力Fig.4 Lateral force of wheelset

2 车-线-桥耦合系统动力特性分析

基于第一节建立的数值模型,设置150～350 km/h共5种速度等级,研究地震激励和车辆运行速度对车辆动力学性能、轨道和桥梁振动特性的影响。为消除车辆上桥前的初始状态对整个耦合系统振动性能的影响,预留50 m的运行距离。

2.1 加速度响应

图5是不同运营速度下地震激励引起的车体垂向加速度和横向加速度的峰值变化图。由图可知:车体加速度在时程上差异较大,随着车辆运行速度的增加,车体垂向加速度和车体横向加速度总体呈上升趋势。对不同运营速度下有、无地震激励车辆过桥的运行状态进行数值模拟,得到150 km/h速度下车体垂向加速度的平均值为0.34 m/s2,车体横向加速度的平均值为0.08 m/s2,350 km/h速度下车体垂向加速度的平均值为0.72 m/s2,车体横向加速度的平均值为0.14 m/s2,计算得到车辆运行速度由150 km/h变化到350 km/h,车体垂向加速度的变化率为111.7%,车体横向加速度的变化率为75%。对比表6中有、无地震激励下车体加速度可知,地震激励对车体加速度影响显著,且在地震激励下车辆运行速度对车体垂向加速度的影响大于对车体横向加速度的影响。

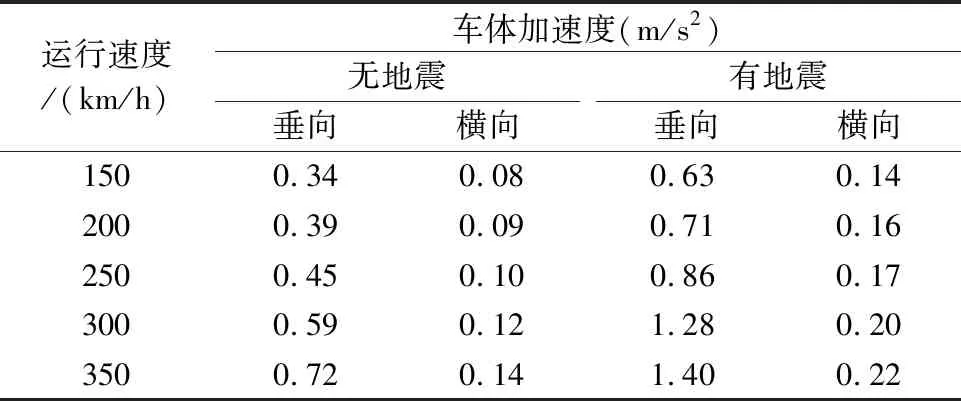
表6 车体加速度的平均值

图5 不同运营速度下车体加速度Fig.5 Vehicle acceleration at different operating speeds

车体的垂向、横向加速度功率谱密度如图6所示,由图可知,对垂向振动:150～350 km/h速度的振动频率分别为3.0 Hz、4.8 Hz、5.8 Hz、7.8 Hz、8.8 Hz,说明在地震激励下,速度的增加会影响车体垂向振动频率偏移。尤其是350 km/h的速度下,车体的垂向加速度增加明显。对比桥梁的自振频率可知,350 km/h的速度下,车体的垂向振动频率为8.8 Hz,与桥梁的一阶垂向振动频率8.82 Hz接近。由此可知,当地震激励作用时,车辆的运行速度增加会导致车体垂向振动频率偏移;桥梁的自振特性对地震激励自下而上的传递影响显著,对车体垂向振动影响显著。对横向振动:150～350 km/h速度的振动频率分别为3.8 Hz、4.8 Hz、6.8 Hz、8.5 Hz、9.7 Hz,说明在地震激励下,速度的增加会影响车体横向振动频率偏移。尤其是300 km/h的速度下,车体的横向加速度增加明显,对比桥梁的自振频率可知,300 km/h的速度下,车体的横向振动频率为8.7 Hz,与桥梁的一阶横向振动频率7.51 Hz接近。由此可知,当地震激励作用时,车辆的运行速度增加会导致车体横向振动频率偏移;桥梁的自振特性对地震激励自下而上的传递影响显著,对车体横向振动影响显著。对于一些影响较为显著的桥梁振动频率对应的模态振型矢量图如图6所示。因此,地震激励作用下,桥梁的自振特性对地震激励自下而上的传递影响显著,对车体振动和车辆运行的平稳性影响显著。

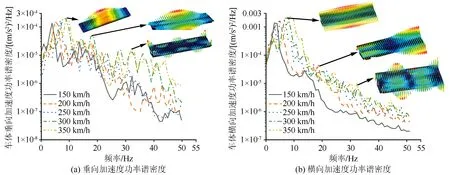
图6 不同运营速度下车体加速度功率谱密度Fig.6 Power spectral density of vehicle acceleration at different operating speeds

本文参考了《高速铁路设计规范》[21]中桥梁挠度的相关规定以及《列车-轨道-桥梁动力相互作用理论与工程应用》[3]中对于桥梁位移和振动加速度监测点的布置,对线-桥系统取跨中数据研究,消除列车上下桥时运行状态发生改变产生的边界效应。图7是不同运营速度下地震激励引起的轨道板垂向振动加速度和横向振动加速度的峰值变化图。由图可知:地震激励对于轨道板的振动加速度有显著的影响,尤其是在4 s附近,轨道板的垂向振动加速度和横向振动加速度均明显增大。车辆运行速度对于轨道板的垂向振动加速度和横向振动加速度均有显著的影响。随着速度的增加,轨道板的垂向振动加速度与横向振动加速度总体均呈上升趋势,尤其350 km/h速度对横向振动加速度和垂向振动加速度的影响都十分显著。图8是不同运营速度下地震激励引起的桥梁垂向振动加速度和横向振动加速度的峰值变化图。由图可知:不同运营速度下桥梁的振动加速度总体变化趋势基本一致,但局部存在明显差异,并非完全对应。桥梁结构响应对于地震激励较为敏感,速度变化对桥梁结构响应的影响仅在局部时间比较显著。

图7 不同运营速度下轨道板振动加速度Fig.7 Vibration acceleration of track slab at different operating speeds

图8 不同运营速度下桥梁振动加速度Fig.8 Vibration acceleration of bridge at different operating speeds

不同运营速度下,地震作用引起的轨道板和桥梁的垂向振动加速度以及横向振动加速度的变化率如表7所列。对比不同速度下的轨道板和桥梁的振动加速度的变化率可知,总体趋势上地震激励对轨道板和桥梁的横向振动的影响大于对垂向振动的影响。在300 km/h速度时,地震激励对轨道板垂向振动的影响大于对横向振动的影响,地震激励在300～350 km/h速度范围内对轨道板振动的影响显著。

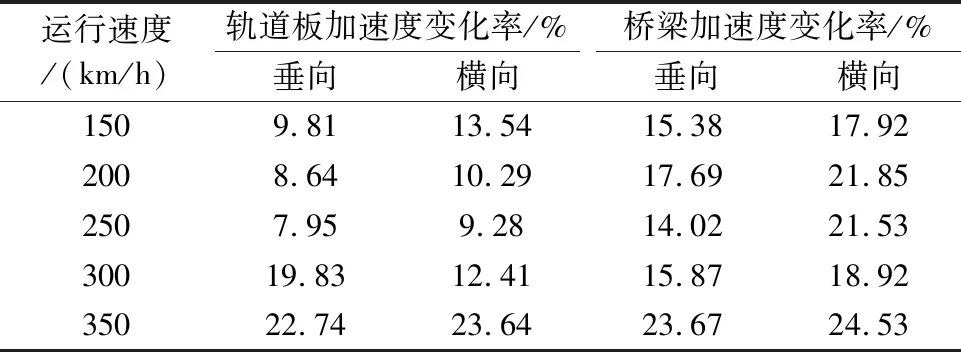
表7 轨道板和桥梁加速度变化率

2.2 位移响应

图9是不同运营速度下地震激励引起的轨道板垂向位移和横向位移的峰值变化图。由图可知:对于轨道板而言,随着速度的增加,垂向位移峰值和横向位移峰值总体呈上升趋势,速度对垂向位移峰值的影响比对横向位移峰值的影响大。在150～250 km/h速度范围内,速度对于轨道板横向位移峰值的影响较小。在300～350 km/h运营速度下,车辆运行速度对于轨道板横向位移峰值和垂向位移峰值的影响开始显著,轨道板垂向位移对车辆运行速度的变化更为敏感。

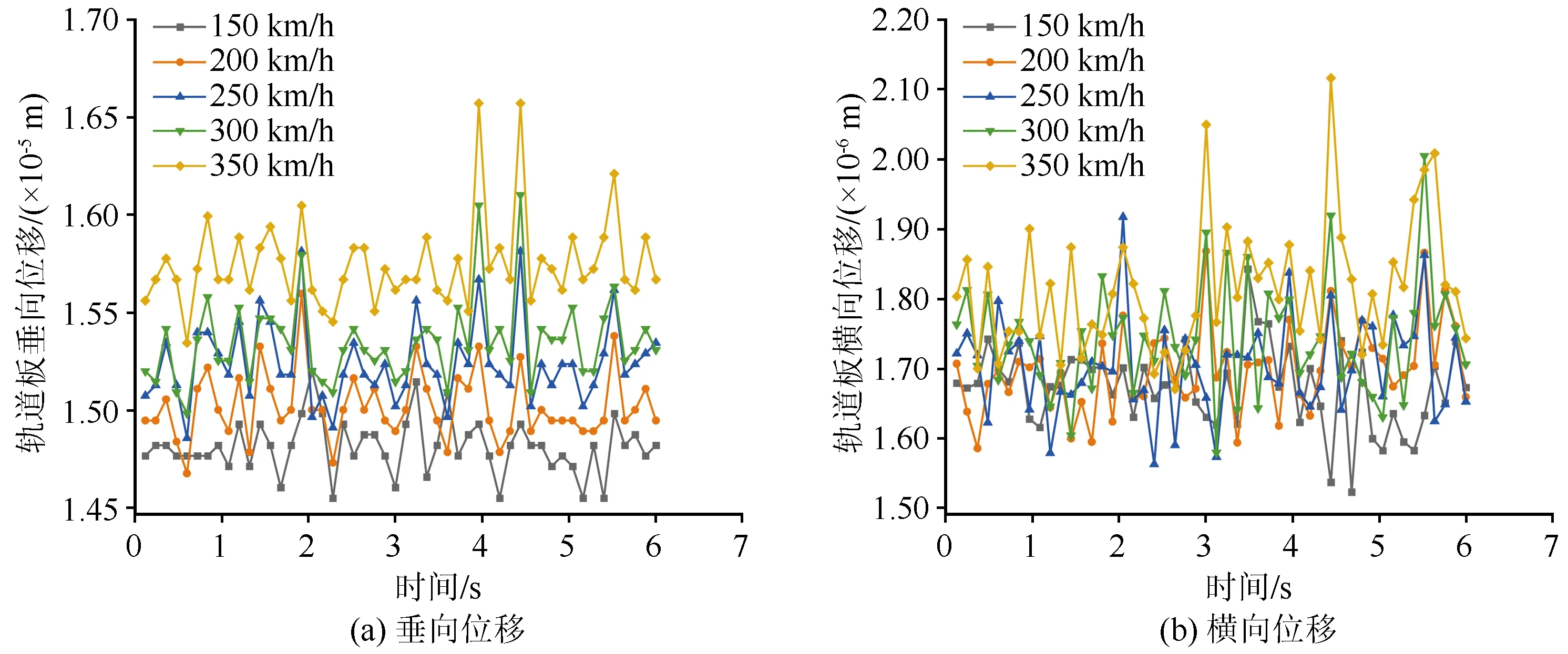
图9 不同运营速度下轨道板位移Fig.9 Track slab displacement at different operating speeds

图10是不同运营速度下地震激励引起的支撑层垂向位移和横向位移的峰值变化图。由图可知:地震激励对支撑层位移响应影响显著,不同时间下支撑层位移峰值相差较大。随着速度的增加,垂向位移峰值和横向位移峰值总体呈上升趋势,车辆运行速度对垂向位移峰值的影响比对横向位移峰值的影响大。在150～250 km/h速度范围内,速度对于支撑层横向位移峰值的影响较小。当车辆运行速度达到300～350 km/h速度后,速度对于支撑层横向位移峰值和垂向位移峰值的影响开始显著。其中350 km/h速度对横向位移峰值和垂向位移峰值影响都十分显著,支撑层垂向位移对速度变化更加敏感。对比轨道板位移与支撑层位移可以发现,支撑层位移和轨道板位移变化趋势基本一致,二者均可直观反映地震激励下不同运营速度的轨道结构变形情况。

图10 不同运营速度下支撑层位移Fig.10 Support layer displacement at different operating speeds

不同运营速度下,地震作用引起的轨道板和支撑层垂向位移和横向位移的变化率如表8所列。对比不同速度下的轨道板和支撑层位移的变化率可知,总体趋势上,地震激励对轨道板和支撑层横向位移的影响大于对垂向位移的影响。结合表7,可以得到地震激励对轨道结构和桥梁结构的横向振动的影响大于对系统的垂向振动的影响。对比不同运营速度下各结构振动响应的变化情况可知,虽然桥梁振动加速度幅值较小,但地震激励引起的桥梁振动加速度变化率显著大于支撑层和轨道板的振动响应的变化率,即桥梁结构对地震激励敏感程度大于轨道结构。因此,可考虑以桥梁振动加速度间接检测地震激励作用下轮轨间的相互作用力的剧烈程度。

表8 轨道板和支撑层位移变化率

3 结论

本文建立了高速铁路桥梁区段车辆-轨道-桥梁耦合系统动力学模型,基于《建筑抗震设计规范》设计地震反应谱,分析了不同速度等级下地震激励对车辆动力学性能、轨道板、支撑层以及桥梁结构振动特性的影响,结论如下:

(1) 地震激励对车辆-轨道-桥梁耦合系统的振动特性产生了显著的影响,其影响规律由轮轨动态相互作用和桥轨动态相互作用主导;

(2) 地震激励对轨道板、支撑层和桥梁的横向振动特性的影响大于对垂向振动特性的影响,桥梁结构对地震激励的敏感程度大于轨道结构;

(3) 在地震激励作用下,车辆运行速度的增加会引起车体振动频率的偏移;桥梁的自振特性对地震激励自下而上的传递影响显著,对车体的振动响应和车辆运行的平稳性影响显著;

(4) 车辆的运行速度会影响整个系统的振动特性,在300～350 km/h速度范围内影响显著,车辆运行速度对系统垂向振动特性的影响大于对横向振动特性的影响。