带反射变量微分方程的极限周期解❋

庄晓丽

(中国海洋大学数学科学学院, 山东 青岛 266100)

考虑泛函微分方程

x′(t)=f(t,x(t),x(-t))。

(1)

该方程的特殊点在于反射变量-t。在微分-差分方程的稳定性研究中,该类包含反射自变量的微分方程有着重要的应用[1]。 Afidabizadeh和Wiener[2]以及Gupta[3]相继研究了该类包含反射自变量的微分方程的两点边值问题。 对于方程(1),Afidabizadeh等[4]证明了如下结论:若f关于t是一致概周期的,则它的解的有界性等价于概周期性。朴大雄[5-6]研究了线性方程

x′(t)+ax(t)+bx(-t)=g(t),b≠0,t∈R

(2)

以及相关的非线性方程

x′(t)+ax(t)+bx(-t)=
F(t,x(t),x(-t)),b≠0,t∈R

(3)

的概周期解和伪概周期解的存在唯一性问题。

本文的目的是研究另一类概周期型解,即方程(2)和方程(3)的极限周期解。到目前为止,关于微分方程极限周期解的研究工作非常少,仅见文献[7-9],而对带有反射自变量方程的极限周期解的研究,尚未见报道。

为了叙述本文的主要结果,需要先介绍相关的预备知识并证明几条引理。

1 预备知识和几条引理

本节引入关于概周期函数、极限周期函数、一致概周期函数以及一致极限周期函数的基本概念及性质,为下面的研究做准备。

考虑定义在实轴R=(-∞,+∞)上的实值连续函数f(t),即f(t)∈C(R)。

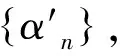
这是Bochner在1927年给出的概周期函数的定义,它与Bohr概周期函数的定义是等价的[10-12]。

令LP(R)表示所有极限周期函数组成的集合。显然,LP(R)⊂AP(R)并不是线性空间。 令h∈LP(R),则存在以Tn>0为周期的连续周期函数列hn,使得

对于LP{Tn}(R),易证下面的引理。

引理1如果有f,g∈LP{Tn}(R),α,β∈R,则αf+βg∈LP{Tn}(R),即LP{Tn}(R)是线性空间。

证明 由于f,g∈LP{Tn}(R),则分别存在连续周期函数列{fn},{gn}使得,对任意t∈R有

fn(t+Tn)=fn(t),gn(t+Tn)=gn(t),

且fn(t),gn(t)随n→∞分别一致收敛到f(t),g(t)。

令Fn(t)=αfn(t)+βgn(t),F(t)=αf(t)+βg(t),则

Fn(t+Tn)=Fn(t)。

由于对任意ε>0,存在N>0,使得当n>N时对任意t∈R有

|fn(t)-f(t)|<ε,|gn(t)-g(t)|<ε,

故|Fn(t)-F(t)|<(|α|+|β|)ε。

综上可知,αf+βg∈LP{Tn}(R)。

引理2LP{Tn}(R)是AP(R)的Banach子空间。

证明 由引理1可知,仅需证明LP{Tn}(R)是AP(R)的闭子集。

对于f=f(t),定义f-=f(-t),易得出下面的引理。

引理3若f∈AP(R)(LP(R),LP{Tn}(R)), 则f-∈AP(R)(LP(R),LP{Tn}(R))。

证明 若f(t)∈AP(R)且τ是f(t)的ε-移位数,则集合

T(f,ε)={τ||f(t+τ)-f(t)|<ε,∀t∈R}

是相对稠密的。由此可知,

即集合

{τ||f(-(t+τ))-f(-t)|<ε,∀t∈R}

是相对稠密的,故f-∈AP(R)。

若f(t)∈LP(R),则存在一列连续周期函数{fn(t)}一致收敛于f(t)。由此可知,连续周期函数列{fn(-t)}一致收敛于f(-t),即f-∈LP(R)。

若f∈LP{Tn}(R),则存在一列连续周期函数{fn(t)}一致收敛于f(t)且{fn(t)}满足fn(t+Tn)=fn(t)。因此,连续周期函数{fn(-t)}一致收敛于f(-t)且{fn(-t)}满足fn(-t+Tn)=fn(-t),即f-∈LP{Tn}(R)。

类比一致概周期函数的定义,本文给出一致极限周期函数的定义如下。

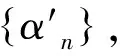
定义4若对于任意紧集W⊂R2,总存在连续周期函数列{Fn(t,x,y)}关于t在W上一致收敛于F(t,x,y),则称连续函数F:R×R2→R关于t在R2上是一致极限周期的。 记LP(R×R2)表示所有一致极限周期函数的集合。

显然,LP(R×R2)⊂AP(R×R2)。下面考虑LP(R×R2)的子集:

LP{Tn}(R×R2)=

{F∈LP(R×R2)|Fn(t+Tn,x,y)=Fn(t,x,y),

(x,y)∈W,n∈N}。

引理4设F∈LP{Tn}(R×R2),φ∈LP{Tn}(R,W),其中W是R2的紧子集,则F(·,φ(·))∈LP{Tn}(R)。

证明 方便起见,记F(t,X)=F(t,x,y),其中X=(x,y)。设W是R2的任一紧子集,F∈C(R×W),则可知F在R×W上是一致连续的,即对于任意ε>0,存在δ>0,使得对于任意X1,X2∈W,当|X1-X2|<δ时,有

由于φ∈LP{Tn}(R,W),故对任意t∈R,φ(t)∈W,且φ(t)是极限周期的。 又F∈LP{Tn}(R×R2),故对于上述ε>0和δ>0,存在N>0,使得当n>N时,有

|φn(t)-φ(t)|<δ,t∈R,

从而

|Fn(t,φn(t))-F(t,φ(t))|≤

|Fn(t,φn(t))-F(t,φn(t))|+|F(t,φn(t))-

又

Fn(t+Tn,X)=Fn(t,X), (t,X)∈R×W,φn(t+Tn)=φn(t),t∈R,

故有Fn(t+Tn,φn(t+Tn))=Fn(t,φn(t))。

因此,F(·,φ(·))∈LP{Tn}(R)。证毕。

2 主要结论及证明

首先考虑线性微分方程

x′(t)+ax(t)+bx(-t)=g(t),b≠0,t∈R,

(4)

其中g(t)是R上的连续函数。

定理1对于任意的g(t)∈LP{Tn}(R),λ2=a2-b2,λ>0,方程(4)都存在唯一的极限周期解x(t)∈LP{Tn}(R)。

证明 存在性:由文献[4]的引理2和引理3可知,对于任意的g(t)∈LP{Tn}(R),

是方程(4)的一个特解。 下面证明x(t)∈LP{Tn}(R)。

对于每一自然数n, 设gn是以Tn为周期的连续周期函数, 且gn一致收敛于g。考虑下面的函数列

xn(t)=

下证xn(t)是一列以Tn为周期的连续周期函数列。

|xn(t+Tn)-xn(t)|=

bgn(-(s+Tn)))ds+

bgn(-(s+Tn)))ds+

b(gn(-(s+Tn))-gn(-s)))ds+

b(gn(-(s+Tn))-gn(-s)))ds|≤

其中

‖gn(t+Tn)-gn(t)‖=

由于gn(t)是一列以Tn为周期的连续周期函数列,即‖gn(t+Tn)-gn(t)‖=0,故xn(t)也是一列以Tn为周期的连续周期函数列。

因为gn(t)一致收敛于g(t),所以,对于任意ε>0,存在N>0,使得当n>N时,对任意的t∈R,有|gn(t)-g(t)|<ε,从而有

|xn(t)-x(t)|=

b(gn(-s)-g(-s)))ds+

b(gn(-s)-g(-s)))ds|≤

由此可知,xn(t)是一列以Tn为周期的连续周期函数列,且xn(t)一致收敛于x(t)。 因此,x(t)∈LP{Tn}(R)。

x′(t)+ax(t)+bx(-t)=0,b≠0,t∈R

的解。 由文献[4]的引理2可知,

下面本文利用压缩映像原理来证明关于非线性方程的定理。

定理2设F∈LP{Tn}(R×R2),且满足Lipschitz条件

|F(t,x1,y1)-F(t,x2,y2)|≤L(|x1-x2|+|y1-y2|),

证明 由引理4可知,对于任意φ∈LP{Tn}(R),有F(·,φ(·),φ-(·))∈LP{Tn}(R)。根据定理1可知,方程

x′(t)+ax(t)+bx(-t)=

F(t,φ(t),φ(-t)),b≠0,t∈R

(5)

存在唯一的极限周期解,记为(Tφ)(t)。这样就定义了一个映射T:LP{Tn}(R)→LP{Tn}(R)。

下面证明T是压缩的。事实上,对于任意φ,ψ∈LP{Tn}(R),方程

x′(t)+ax(t)+bx(-t)=

F(t,φ(t),φ(-t))-F(t,ψ(t),ψ(-t))

有唯一的极限周期解(Tφ-Tψ)(t),且

(Tφ-Tψ)(t)=

F(s,ψ(s),ψ(-s))))+b(F(-s,φ(-s),φ(s))-

F(-s,ψ(-s),ψ(s))))ds+

F(s,ψ(s),ψ(-s)))-b(F(-s,φ(-s),φ(s))-

F(-s,ψ(-s),ψ(s))))ds。

因此,由定理1的证明过程可知

3 结语

本文构造了由极限周期函数组成的特殊集合,并证明了在上确界范数下该集合为Banach空间。在此基础上,利用压缩映射原理,给出了所研究的方程极限周期解存在唯一性的结果。带反射变量的二阶方程的极限周期解的存在唯一性是本文下一步要研究的问题。