微型贯入试验与无侧限抗压强度试验结果的对比❋

董猛荣, 杨俊杰, 阮媚媚, 王思雨, 孙 涛, 王子玉

(1. 海洋环境与生态教育部重点实验室(中国海洋大学), 山东 青岛 266100; 2. 中国海洋大学环境科学与工程学院, 山东 青岛 266100;3. 山东科技大学地球科学与工程学院, 山东 青岛 266590; 4. 海南热带海洋学院生态环境学院, 海南 三亚 572022)

水泥土的无侧限抗压强度是工程设计的一个重要指标。但是对于劣化水泥土这一非均质体不宜采用无侧限抗压强度等单元体试验,应该采用微型贯入等模型试验进行相关研究[1-8]。微型贯入试验可获得劣化水泥土内部连续的贯入阻力,但无法评价对应强度。因此,有必要建立微型贯入试验的贯入阻力与无侧限抗压强度的定量关系。

盛海洋等[9]认为可用3～5 d对桩身静力触探曲线贯入阻力值预估桩身无侧限抗压强度,并提出了预测式,但未进行相关试验验证。卢发亮和王晓声[10]采用静力触探和无侧限抗压强度试验,对比分析了成桩7 d的粉喷和浆喷两种水泥土搅拌桩不同深度处的桩身比贯入阻力和无侧限抗压强度。其中,静力触探采用的是探头直径3.57 cm、锥尖角度60°、侧壁面积200 cm2的双桥探头。张浩和顾长存[11]在对卢发亮和王晓声的试验数据分析的基础上,得到了比贯入阻力与无侧限抗压强度的关系,并结合7 d龄期与28 d龄期无侧限抗压强度的关系,提出了利用7 d龄期的比贯入阻力评价28 d龄期无侧限抗压强度的方法。由于试验数据取自同一桩体的不同深度,所以水泥土试样的强度分布范围较窄,换算关系具有一定的局限性。李国维[12]等采用与只管法对成桩7 d的水泥土搅拌桩进行静力触探试验,认为不同土层 7 d 龄期的静力触探锥尖阻力与芯样 28 d 强度具有良好的线性相关性。提出了快速检测水泥土搅拌桩强度的方法。Kitazume等[13]利用直径为0.56 mm的探头对不同水泥掺入比的水泥土进行微型贯入试验,并与无侧限抗压强度进行了对比,探针在2、5、10 mm处的贯入阻力与无侧限抗压强度呈线性关系,但未给出二者之间的换算关系式。Consoli等[14]制备了不同固化剂种类、掺入比、养护龄期的水泥土试样,实施了微型贯入试验。探头为平端,探头直径分别为7.98、10.29、13.82和20.26 mm,贯入深度为10.0 mm。对于强度较高的试样采用直径较小的探头以避免贯入阻力值超出量力环量程。比贯入阻力随着贯入深度线性增加。贯入深度10 mm时的比贯入阻力与无侧限抗压强度呈线性关系,据此可将贯入试验结果换算成无侧限抗压强度,换算关系与固化剂种类、掺入比、养护龄期无关。但是,该换算关系没有考虑探头直径对比贯入阻力的影响,且拟合直线有截距。

另一方面,通过整理探头(探头直径3.57 cm)及桩在三种黏性土中的静力贯入试验资料,发现当探头锥尖角度小于60°时,贯入阻力随锥尖角度的增大而减小;当锥尖角度超过60°后,贯入阻力或趋于稳定或呈增大趋势[15]。

对于微型贯入试验,探头几何尺寸是影响贯入阻力的重要因素,每位学者采用的探头直径和探头锥尖角度均不相同。并且Kitazume等[13]和Consoli等[14]虽然都得到了贯入阻力或比贯入阻力与无侧限抗压强度之间的线性关系,但该关系均取决于某贯入深度。

本文针对不同原土种类、不同水泥掺入比、不同含水率、不同养护时间的水泥土试样,实施不同锥尖角度、不同探头直径的微型贯入试验和无侧限抗压强度试验,研究探头几何尺寸对微型贯入试验结果的影响,及微型贯入试验结果与无侧限抗压强度试验结果的对应关系。基于研究结果,可利用贯入曲线推测无侧限抗压强度。

1 试验概况

1.1 试验材料

试验用土为上海市奉贤丰诚试剂厂生产的纯高岭土以及日照岚山港海相软土、青岛胶州湾海相软土;试验用水泥采用山东莒州水泥有限公司生产的42.5#复合硅酸盐水泥。试验用土物理性质见表1。

表1 试验用土物理性质

1.2 试验装置及试样制备方法

贯入试验制样桶如图1所示。为尽可能的减小边界效应,探头直径3.4 mm的贯入试验制样桶选用下内径85.0 mm,上内径90.0 mm,高105.0 mm的塑料烧杯(见图1(a));探头直径7.0和10.0 mm的贯入试验试样桶选用下内径135.0 mm,上内径150.0 mm,高150.0 mm的塑料桶(见图1(b))。

图1 微型贯入试验试样桶

制备微型贯入试样时,为保证试样的均匀性,将水泥土分三次填入试样桶中,每次震动20次以排除气泡,填样完成后用小型制样搅拌机上下搅拌3次、刮平表面封保鲜膜后进行标准养护。

无侧限抗压强度试验用试模和制备的试样如图2所示,试样直径50.0 mm,高100.0 mm。

图2 无侧限抗压强度试验模具及试样

制备无侧限抗压强度试样时,同样分3次填入,每次震动20次。

如图3所示,微型贯入试验设备为应变控制式,贯入速度为2.0 mm/min,每行进0.2 mm记录贯入阻力数值一次,贯入至40.0 mm处时停止贯入。将微型贯入试验设备简单改装后可实施无侧限抗压强度试验,应变速率为1.0 mm/min,每0.2 mm记录数据一次,试样已明显破坏时停止试验。

图3 微型贯入仪及无侧限抗压强度试验仪

1.3 试验方案

1.3.1 探头几何尺寸对微型贯入试验结果的影响 探头几何尺寸为探头锥尖角度及探头直径(见图4)。选用不同锥尖角度及直径的探头进行微型贯入试验,为避免侧摩阻力的影响,探杆直径略小于探头直径,试验用探头尺寸见图5。

图4 探头锥尖角度α与探头直径d的定义

图5 试验用探头几何尺寸

具体的试验方案见表3、表4。

表3 探头锥尖角度对微型贯入试验结果影响的试验方案

表4 探头直径对微型贯入试验结果影响的试验方案

1.3.2 微型贯入试验与无侧限抗压强度试验结果的对比 针对同一条件下的水泥土试样分别进行微型贯入试验及无侧限抗压强度试验。所用探头直径为3.4 mm,锥尖角度为60°。试验方案见表5。

表5 微型贯入与无侧限抗压强度试验结果对比的试验方案

2 试验结果与分析

2.1 探头几何尺寸对微型贯入试验结果的影响

2.1.1 探头锥尖角度对微型贯入试验结果的影响 微型贯入试验得到的是贯入阻力(N)与贯入深度(mm)的关系,在此分别用探头平面投影面积和探头直径进行归一化处理,得到比贯入阻力pc(kPa)与比贯入深度d的关系,简称为贯入曲线。图6为不同锥尖角度的高岭土水泥土贯入曲线。试样的掺入比、养护龄期相同,强度不同由含水率不同导致。开始时贯入曲线随比贯入深度近似线性增加(部分试样由于锥尖的影响在贯入深度很小时可能出现贯入阻力增大不明显的现象),达到一定深度后出现拐点,最后趋于稳定。这一结果与水泥土的强度无关。因此,可以得到图7所示的贯入曲线模式图。在此将最后稳定的比贯入阻力定义为贯入强度,pu。

图6 不同锥尖角度的高岭土水泥土贯入曲线

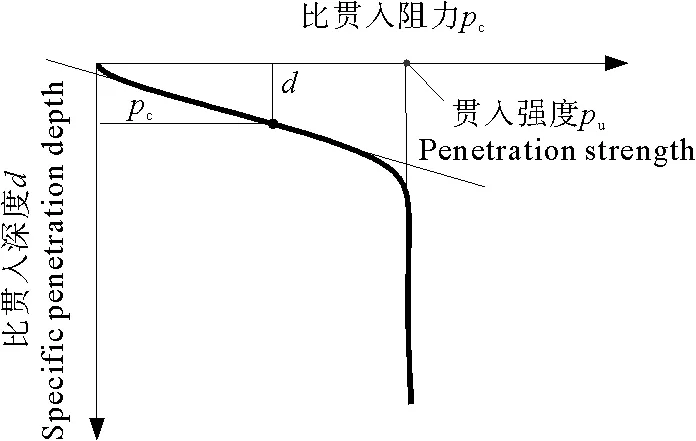
图7 贯入曲线模式图

从图6可以看出,锥尖角度越大的探头比贯入阻力随比贯入深度的增长越迅速,即贯入曲线斜率越大。在所有锥尖角度探头的比贯入阻力均未达到拐点时,同一比贯入深度处(如比贯入深度为1.5时),锥尖角度越小的探头比贯入阻力越小。

图8为根据图7定义的贯入强度和图6的试验结果整理的探头锥尖角度与高岭土水泥土比贯入深度为1.5时的比贯入阻力及贯入强度之间的关系。图中空心图例为贯入强度,实心图例为比贯入深度为1.5时的比贯入阻力。

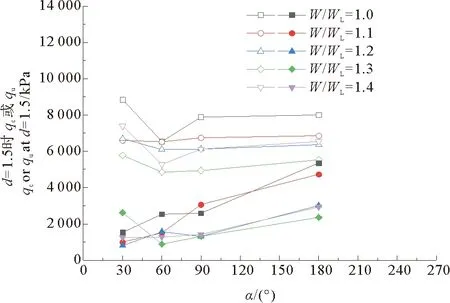
图8 锥尖角度与贯入强度和比贯入深度为1.5时的比贯入阻力关系

在贯入阻力曲线达到拐点前,除个别异常点外,比贯入深度为1.5时,比贯入阻力均随着锥尖角度的增大而增大。贯入强度在探头锥尖角度为30°时最大,随着锥尖角度的增加逐渐减小,当锥尖角度为60°时达到最小,随后随锥尖角度的增加略微增大之后趋于稳定。该结果与现场的贯入阻力结果[9]趋势一致。

鉴于探头锥尖角度60°的探头最为常用,将锥尖角度为30°、90°和180°时的贯入强度与锥尖角度为60°时的贯入强度的关系整理后得到图9。如图9所示,锥尖角度90°和180°贯入强度基本相同,与锥尖角度60°时贯入强度关系可用式(1)表示,相关系数R2=0.915 9。

图9 探头锥尖角度60°时贯入强度与锥尖角度30°和90°或180°时贯入强度关系

pu60°=0.891 7pu90°/180°。

(1)

式中:pu60°为探头锥尖角度为60°时的贯入强度;pu90°/180°为探头锥尖角度为90°或180°时的贯入强度。

同样,锥尖角度30°贯入强度与锥尖角度60°贯入强度关系可用式(2)表示,相关系数R2=0.914 2。

pu60°=0.832 6pu30°。

(2)

式中pu30°为探头锥尖角度为30°时的贯入强度。

根据式(1)或式(2),可以进行不同探头锥尖角度所得贯入强度之间的换算。

2.1.2 探头直径对微型贯入试验结果的影响 探头锥尖角度60°、不同探头直径(D)的贯入曲线如图10、图11所示。图10为高岭土水泥土贯入曲线;图11为海相软土水泥土贯入曲线。

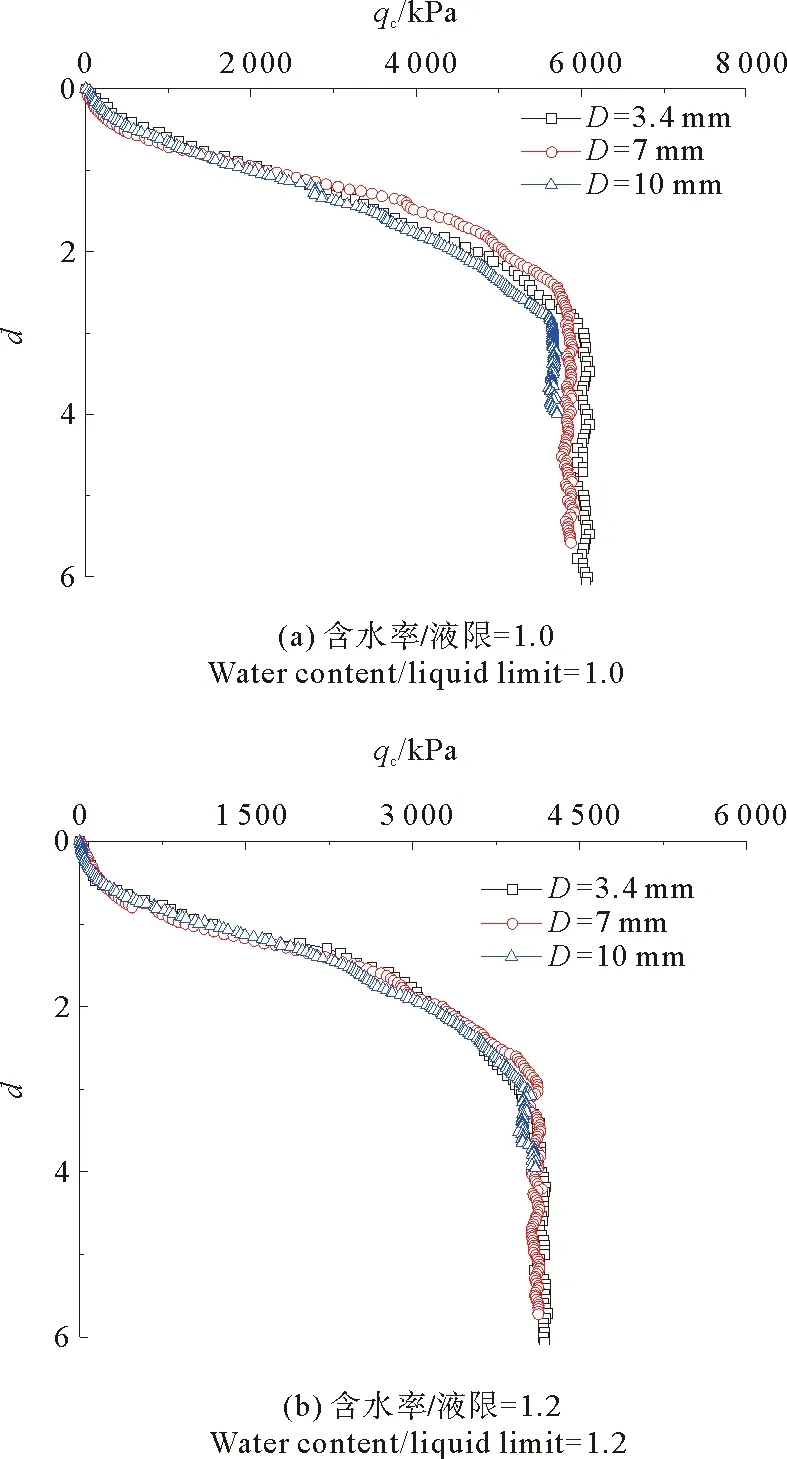
图10 不同探头直径(D)的高岭土水泥土贯入曲线

探头直径对贯入曲线的影响较小,水泥土强度相同,不同直径的探头所对应的贯入曲线变化不大。对比贯入强度发现,探头直径小的试样贯入强度略高。图12、13分别为探头直径对高岭土水泥土和海相软土水泥土比贯入深度为1时的比贯入阻力及贯入强度的影响。

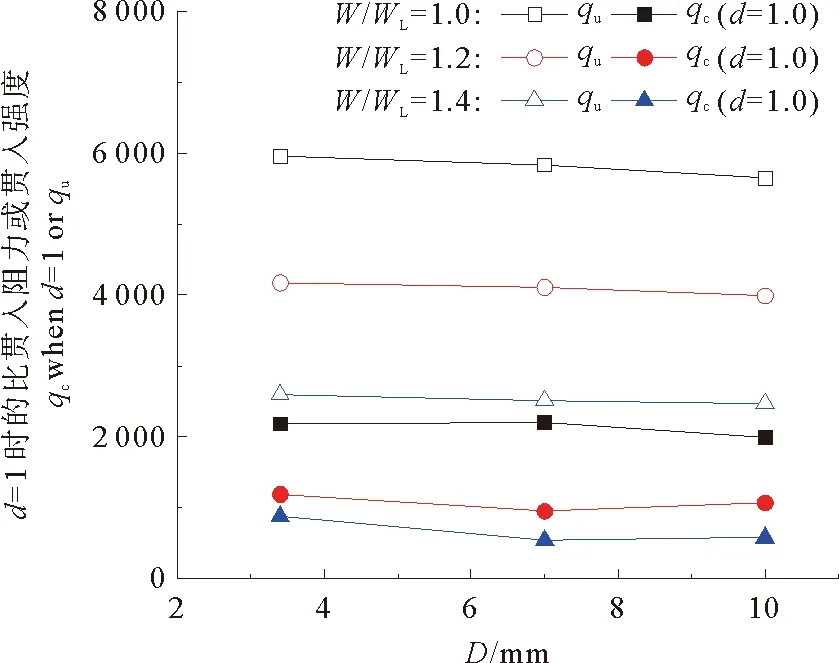
图12 探头直径(D)对高岭土水泥土比贯入深度为1时的比贯入阻力及贯入强度的影响

图13 探头直径(D)对海相软土水泥土贯入深度为1时的比贯入阻力及贯入强度的影响

比贯入深度为1时的比贯入阻力随探头直径的变化规律不明显。贯入强度随着探头直径的增大呈缓慢降低的趋势,探头直径3.4 mm(对应面积为9.074 6 mm2)的探头所得的贯入强度约比探头直径7.0 mm(对应面积为38.465 mm2)的探头所得的贯入强度大2.5%左右,比探头直径10.0 mm(对应面积为78.5 mm2)的探头所得贯入强度大5%左右,贯入强度与探头直径呈线性关系,鉴于后续微型贯入试验与无侧限抗压强度试验结果关系研究中所用的探头为直径为3.4 mm的探头,将7.0、10.0 mm直径探头与3.4 mm直径探头所得贯入强度的比值与探头直径的关系进行整理后,得到图14。

贯入阻力的数值与探头直径存在很大的相关性,相关系数R2=0.947 5,可将拟合式转化为:

pu3.4=pu/(-0.008D+1.021 4)。

(3)

式中:pu3.4为探头直径为3.4 mm时的贯入强度;pu为探头直径为D的探头贯入强度。

通过式(3)可将任意直径(3.4～10.0 mm范围内)探头所得的贯入强度转换为直径3.4 mm探头所得的贯入强度,也可将任意两个直径(3.4～10.0 mm范围内)的探头所得的贯入强度相互转换。

2.2 微型贯入试验与无侧限抗压强度试验结果对比

高岭土水泥土及海相软土水泥土试样的贯入曲线见图15、图16。

图15 高岭土水泥土微型贯入试验结果

图16 海相软土水泥土微型贯入试验结果

高岭土水泥土及海相软土水泥土试样通过无侧限抗压强度试验获得的应力应变关系曲线见图17、图18。

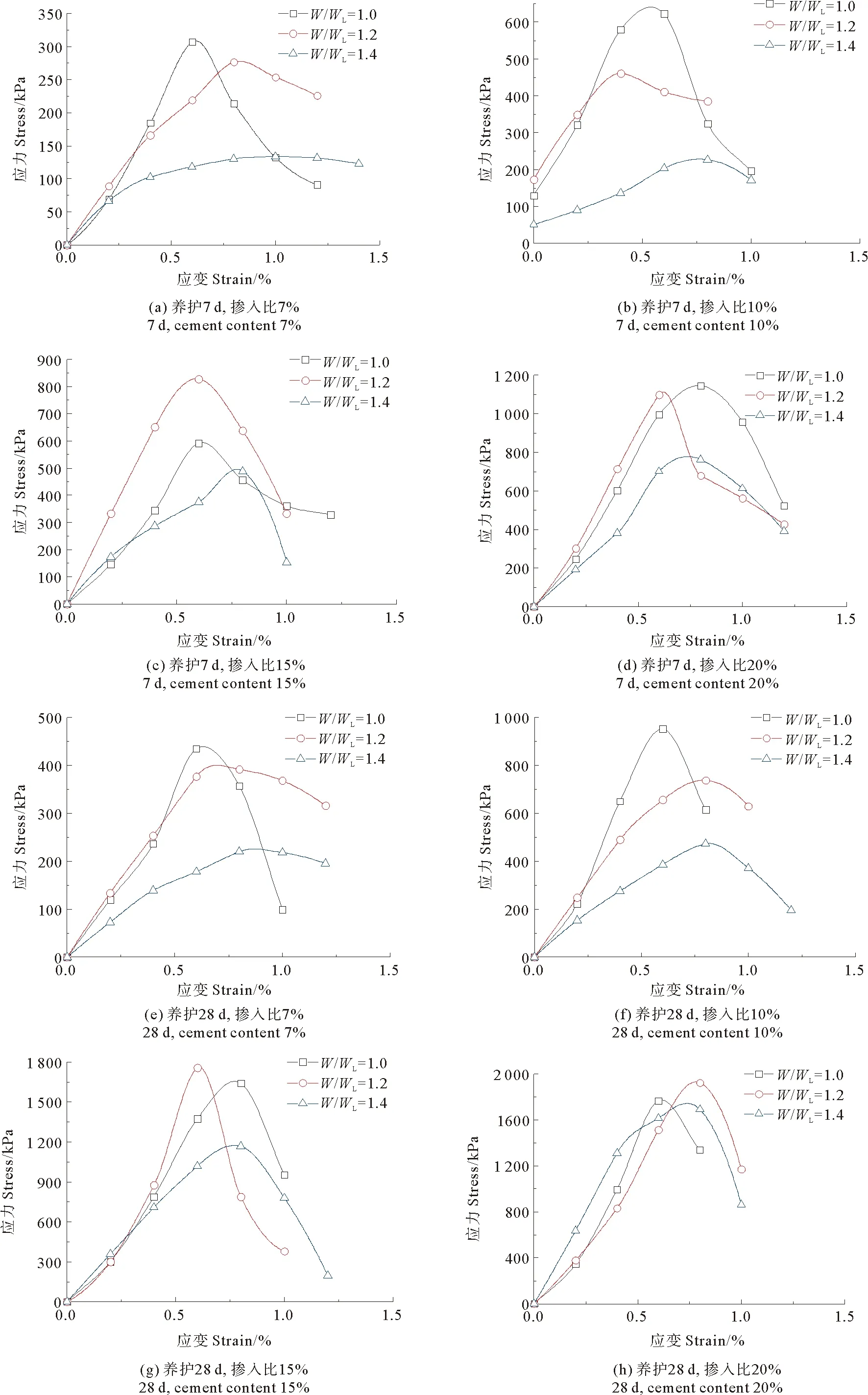
图17 高岭土水泥土应力应变关系

图18 海相软土水泥土应力应变关系

应力应变曲线均出现峰值,取应力峰值为无侧限抗压强度。

如图7、15、16所示,比贯入阻力与比贯入深度有关,在线性增加的阶段,可用斜率描述比贯入阻力与比贯入深度的关系。图19即为整理的贯入曲线达到拐点前直线段斜率与无侧限抗压强度的关系。

比贯入阻力拐点前直线段斜率与无侧限抗压强度呈线性关系R2=0.888 9。

qu=0.115 4k。

(4)

式中:qu为无侧限抗压强度;k为贯入曲线直线部分斜率。

可用贯入曲线拐点前直线段斜率通过式(4)换算无侧限抗压强度。

另一方面,贯入强度与无侧限抗压强度的关系则由图15、16和图17、18得到(见图20)。

图20 贯入强度与无侧限抗压强度关系

无侧限抗压强度随贯入强度的增大而增大。当强度较小时,贯入强度与无侧限抗压强度相关性较好,强度较大时,数据离散性较大,可能是贯入试验使用的探头直径小,探杆出现倾斜,影响试验结果准确性的缘故。将贯入强度与无侧限抗压强度关系进行线性拟合得到式(5),相关系数R2=0.859 1。

qu=0.049 5pu。

(5)

式中:qu为无侧限抗压强度;pu为贯入强度。

利用贯入强度和式(5)可得到相应的无侧限抗压强度。

试验通过改变水泥土形成条件(原土类型、水泥掺入比、含水率、养护龄期),得到了不同强度的水泥土,且强度变化范围较大,说明水泥土强度的形成条件对贯入曲线拐点前直线段斜率及贯入强度与无侧限抗压强度之间的关系没有明显影响。

3 结论

本文探讨了探头锥尖角度和直径对微型贯入试验结果的影响及微型贯入试验与无侧限抗压强度试验结果的关系,得出如下结论。

(1)探头锥尖角度和直径对贯入曲线性状没有影响,即贯入阻力随贯入深度线性增加,达到某一贯入深度时贯入曲线出现拐点,贯入阻力趋于稳定,可定义此时的比贯入阻力为贯入强度。

(2)探头锥尖角度越大,达到拐点前贯入曲线直线段斜率越大,即贯入阻力随贯入深度增长越快;贯入强度在探头锥尖角度为30°时最大,随着锥尖角度的增加逐渐减小,当锥尖角度为60°时达到最小,随后随锥尖角度的增加略微增大之后趋于稳定。

(3)锥尖角度为30°、90°和180°时的贯入强度与锥尖角度为60°时贯入强度的关系呈线性关系。

(4)不同探头直径的贯入曲线在拐点前几乎重合,说明探头直径对比贯入曲线的影响可忽略不计。但贯入强度随探头直径的增大呈线性减小趋势,探头直径3.4 mm的贯入强度比7.0 mm的贯入强度增大2.5%,比10.0 mm的贯入强度增大5.0% 。

(5)可用贯入曲线拐点前直线段斜率换算无侧限抗压强度,也可利用贯入强度换算无侧限抗压强度。水泥土强度的形成条件对贯入曲线拐点前直线段斜率及贯入强度与无侧限抗压强度之间的关系没有明显影响。