Sine-Gordon方程二重网格方法的高精度分析

王芬玲

(许昌学院 数理学院,河南 许昌 461000)

二重网格方法通常被认为是求解非线性方程的一种有效的离散化技术.关键是采用二重网格格式对方程中的非线性项进行线性化处理.该方法的基本思想是先在粗网格H上求解非线性或非对称不定问题,然后在细网格h(h≪H)上用牛顿迭代法求解线性问题.[1]对于半线性抛物方程提出了向后欧拉全离散二重网格方法,并讨论了该格式的超收敛性.[2]建立了一种用扩展混合有限元法离散非线性反应扩散方程(含非线性压缩系数)的双网格算法,然后详细分析了扩展混合有限元解的误差估计.此外,[3]提出了一种求解二维时变Navier-Stokes问题的全离散二重网格有限元方法,并推导了该方法离散解最优阶的误差估计.

Sine-Gordon方程是一个正弦函数,用于波传播、经典晶格动力学、生物膜扩展、晶体缺陷扩展、相对论场论等领域. Sine-Gordon方程也可用于解释一系列实验地震数据、应变波建模、与断层动力学和俯冲板块相关的结构,以及慢震、间歇性震颤、慢滑(ETS)事件和震颤迁移模式.[4]采用不同的分析方法来求解Sine-Gordon, 在此基础上用三维和二维图解的方式对所得结果的动力学属性进行了强调和描述.[5]利用扩展的tanh函数方法进一步求出时空分数阶非线性偏微分方程的一般行波解,即时间分数阶非线性Sine-Gordon方程和Klein-Gordon方程.对描述光脉冲在光纤波导中传输的耦合Sine-Gordon方程进行分析研究.[6]利用扩展的G′/G-展开法构造了双曲型和三角型函数的解,然后利用扩展的Jacobi椭圆型函数展开法导出了Jacobi椭圆型、双曲型和三角型函数的解.

考虑如下Sine-Gordon方程

(1)

其中,Ω 是有界凸多边形区域,X=(x,y),α,β,γ是常数,f(X,t)是已知给定的充分光滑函数.

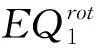
1 单元的构造和性质及问题的变分形式

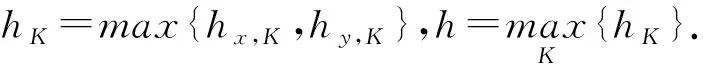
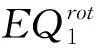
利用文[7]和[8]中的结论可得下面的性质.

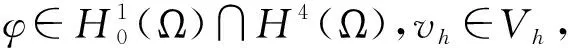
(2)

2 全离散逼近格式和超逼近分析

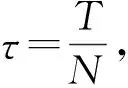
接下来,引入以下算子记号:

考虑方程(2)的全离散逼近格式:求unh∈Vh,使得对于2≤n≤N,满足

(3)

接下来,给出全离散格式的超逼近分析．

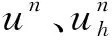
证明令t=tn-1和t=tn+1,有

(4)

(5)

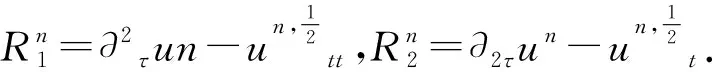
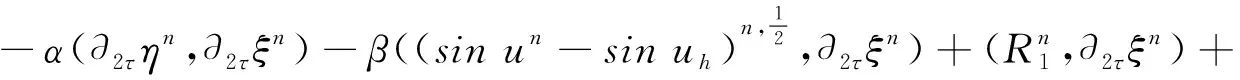
(6)

根据内积的定义,得到如下等式

(7)

(8)

(9)

现在估计式(6)右边的三项.根据插值理论,Cauchy-Schwarz不等式和Young不等式, 可以得到以下估计式

(10)

(11)

(12)

(13)

(14)

最后,根据引理1和Young不等式,可知A6的估计式

(15)

将式 (7)-(15) 代入式 (6), 得

(16)

更进一步,式 (16) 等号两边同时乘以2τ,则

(17)

将式 (17)中的n替换为i,然后对i从1,…,n求和,得

(18)

根据式 (18), 得到

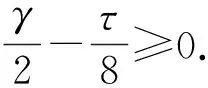
那么,以下不等式成立

(19)

将式 (19)代入式 (18),并对其结果应用离散的Grönwall不等式,存在τ1≥0,

当τ≤τ1时,得

(20)

从而,定理1得证.

3 二重网格的算法及超逼近和超收敛分析

(21)

(22)

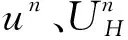
(23)

(24)

证明：通过定理1可知(23)式是显然成立的,接下来要证明(24)式成立.

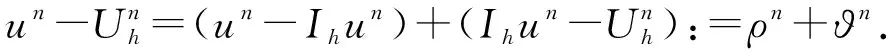
通过Taylor展开可得

其中u*=θUH+(1-θ)UH.根据方程(1)和(22),对于任意vh∈Vh,得误差方程

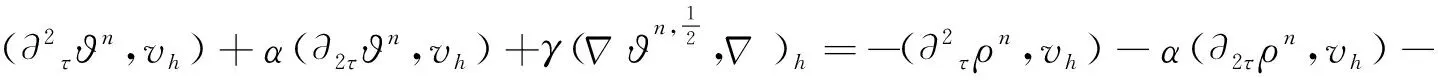
(25)

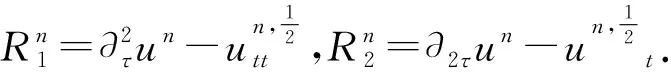
(26)

根据插值理论,Cauchy-Schwarz不等式和Young不等式可得

(27)

根据引理1可知

B3=0.

(28)

根据Cauchy-Schwarz不等式,Young不等式可得

通过嵌入定理和(23)式可得

(29)

根据引理1可得

(30)

将(26)-(30)式代入到(25)式可得

(31)

更进一步,式 (31) 等号两边同时乘以2τ,则

(32)

将式 (27)中的n替换为i,然后对i从1,…,n求和,得

(33)

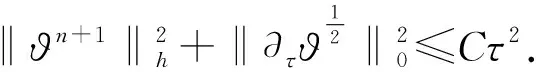
(34)

定理2证毕.

类似于文献[7]定义插值后处理算子Π2h,得超收敛结果为