基于非厄密绝热捷径的快速量子态操控研究

董新平, 闫润瑛

(许昌学院 数理学院,河南 许昌 461000)

为了更快地进行可靠的量子操作,基于非厄密体系的“绝热捷径”(STA)技术[1,2]被用于量子信息处理以及波导光学等领域．STA方法主要包括基于不变量方法[3]、无摩擦驱动[4-7]等方法.基于STA方法的量子系统的核心思想是通过对系统的哈密顿函数进行设计,使量子系统可以在绝热过程中从给定的初始态更快地演化到期望的终态．同时通过非绝热消除可以在较短的时间内实现与绝热情形相同的目标．不仅加快了量子运算的速度,同时大幅度减轻了系统受到的噪声环境的退相干影响．

以上的快速绝热方法通常需要增加不同能级之间的耦合强度才能实现更快的量子系统演化[8]．在有些量子系统中,受到量子体系特征参数以及实验条件的限制,能级之间的耦合强度并不能任意选取,并且过大的耦合还会降低系统的保真度．通过对厄密体系的研究和推广提出了基于非厄密体系的STA方法[9-11].这种非厄米系统原则上可以在非常短的世间内完成量子系统的演化,但需要根据系统的特征参数对体系的增益和损耗进行复杂的计算．最近一个基于动力学的绝热捷径方法(DASA)提出了一种热力学成本较低、易于设计和调控的非厄米系统绝热方案[12]．利用这个方案可以通过对体系增益和耗散的灵活控制,提供一个高效、可靠,同时能耗较低的量子态控制方案．我们将对此方法进行理论分析和数值模拟研究,为进一步利用非厄密绝热捷径方法快速操控量子态提供有效的帮助．

1 基于动力学的绝热捷径方法

对于一个一般的两能级体系,其不含时的2×2非厄密哈密顿量具有以下形式.

H=σx+(iΔγ+Δω)σz/2+(i∑γ+∑ω)1/2.

(1)

其中,Δγ=γ1-γ2,∑γ=γ1+γ2,∑ω=ω1+ω2,Δω=ω1-ω2,σx,z为泡利矩阵,1为单位矩阵.γ1,2分别对应本征态|λ1,2〉的增益或损耗,ω1,2+iγ1,2表示归一化的势能.体系的本征值λ1,2一般可以取为复数.随着时间的变化,体系的本征值将发生相应的演化,相应的初始态将随时间按以下方式演变.

|ψ(t)〉=e-iHt|ψ(0)〉=c1e-iλ1t|λ1〉+c2e-iλ2t|λ2〉.

(2)

如果期望在随时间的演化过程中一个本征态产生增益或损耗,而同时另一个本征态保持不变,则要求哈密顿量的本征值分别为λ1=x1+iy,λ2=x2,x1和x2为实数．那么本征态|λ1>的振幅将将根据相应本征值中虚部的符号分别产生增强或衰减,而本征态|λ2> 的振幅由于虚部为零,在演化过程中不会产生变化．

以下将通过对公式(1)和公式(2)中哈密顿量本征值进行分析,从而求出满足以上要求的参数．将公式(1)中的哈密顿量进行对角化,H=R-1HdR.

(3)

求解相应的本征值方程H=R-1HdR可以得到以下方程组.

d/c+(-x2+iγ1+ω1) = 0,c/d+(-x2+iγ2+ω2) = 0,
d/c+(x1-iγ1-ω1+iy) = 0,c/d+(x1-iγ2-ω2+iy) = 0.

(4)

(5)

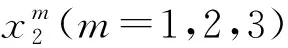
(6)

详细的表达式可参见参考文献[12]的补充材料．相关的两组函数关系Γ2,3(γ2,Δω)如图1所示,其中Δω和γ2的取值范围分别为[0, 10]和[-1, 0]．从图1可以看出,当Γ2(γ2,Δω)的实部在区间(-1,0)之间正值时,相应的Γ3(γ2,Δω)的实部在同一区间保持为零.因此在设计系统的哈密顿量时,可以在选定适当的损耗率γ2后,利用Γ2(γ2,Δω)和Γ3(γ2,Δω)的表达式准确控制增益率γ1.当要求系统的某一本征态快速衰减时,可以利用Γ3(γ2,Δω)选取相应的增益率(接近于零),从而使得另一个本征态保持基本不变;当要求体系的某一个本征态缓慢衰减,同时另一个本征态快速增强以达到目标态时,利用Γ3(γ2,Δω)选取相应比较大的增益率,从而使另一个本征态以指数形式快速增强以快速完成系统的演化.由式(2)还可以看出,系统的一个波函数将在 (γ1+γ2)>0时以指数形式增强,反之当(γ1+γ2)<0时呈指数衰减,同时另一个波函数基本保持不变．

图1 增益率和损耗率实部之间的关系

2 数值模拟计算

以下我们将利用LZ模型以及以上的分析结果,对基于动力学的非厄密绝热捷径方法进行分析和讨论．LZ模型的哈密顿量的一般形式为HLZ(ε,t)=σx-(ε2t)σz,对于一般形式的非厄密方法,当常数耦合强度ε较小时,完成体系的演化一般需要较长时间;增大耦合强度ε又会导致所需增益过大而不易于在实验中实现．

根据对系统哈密顿量本征值和本征态的分析以及式(6)的结果,可以依次使系统按照两个不同性质的哈密顿量进行演化．在第一阶段的演化过程中,使第一个本征态迅速衰减,另一本征态保持基本不变;而在第二阶段的演化中,使第一个本征态缓慢衰减,而第二个本征态快速增强．从而可以使得体系快速完成预期的演化过程．对两个相应过程的增益和损耗的可以利用Γ2,3(γ2,Δω)的性质进行灵活、有效地设计,以达到加快演化速度、降低能耗的目的． 按此方案系统的哈密顿量为

(7)

式中,ti为系统演化的初始时间,T1和T2分别为两个哈密顿量开始施加的时刻,θ(t)为阶跃函数．

根据式(6)和式(7),利用非厄密绝热捷径方法进行数值模拟计算,以实现对系统量子态的快速操控．首先按照按量子态演化的要求选取ti=12.3,T1=12.3,T2=-11.5,然后在H1和H2中分别选取相关的参数.拟合结果为:ω1+iΓ3(γ2,Δω)=0+0.009i,ω2+iγ2=-10-0.95i,ω′1+iΓ3(γ′2,Δω′)=-0.01+2.857i,ω′2+iγ′2=0-0.35i．拟合得到的量子态占据概率随时间的演化结果如图2所示.从图2中可以看出,体系可以在非常短的时间之内完成演化过程．同时可以看出,由于该方案的增益率和损耗率可以取不同的数值,因此可以更好地适用于不同的实验条件,具有更广泛的应用范围．

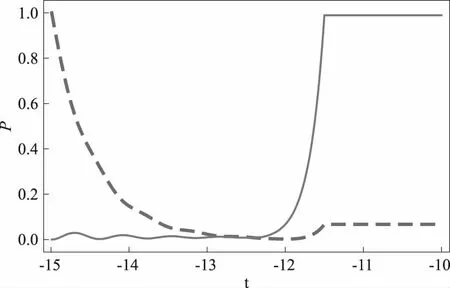
图2 非厄密体系占据概率P随时间的演化

3 结语

通过对基于动力学的非厄密STA方法的分析和研究,实现了对量子态进行快速操控．在具体的设计过程中,用两个连续进行的哈密顿量通过分别调控系统的增益和损耗率实现体系的快速演化． 由于该方法可以根据实验条件的不同灵活设计不同的增益和损耗率,因此该方法不仅设计灵活、可靠,同时还具有适应范围广、能耗低的优点．因此这种方法在理论和实验实现方面都具有潜在的优势．对此方法的进一步推广和应用将为更快操控量子态提供有效的帮助．