基于三维扫描技术的斜裙造型客观评价

施明娟, 刘成霞

(浙江理工大学 a.服装学院; b.服装数字化技术浙江省工程实验室,杭州 310018)

服装造型不仅影响穿着舒适度和美观性,更会影响消费者的购物欲,其中样板结构是服装造型的主要影响因素之一[1]。目前服装造型评价主要通过版师或设计师的主观感觉来确定,缺乏准确度和客观性[2],对于建立科学、客观、可重复的方法来评价服装造型的需求日益迫切。

基于此,许多学者借助图像处理技术[3-4]探究客观的服装造型评价量化指标,如李静[5]通过图像处理技术建立了裙装的客观评价体系;Zulkifli等[6]通过二维图像提取了裤子外轮廓造型指标,定量研究了虚拟与真实裤子之间的造型差异。但二维图像处理会损失实物三维空间中的造型信息,且无法对细节造型进行描述。而三维扫描技术[7]可以获取物体的深度信息,从而实现对服装造型的客观评价及准确表征。陈丽丽等[8]将激光扫描技术与服装穿着平整度的评价研究结合,提取了评价服装肘部穿着折皱的5个指标;李涛等[9]通过[TC2]三维扫描技术研究了样板结构松量的变化对短裤截面廓形变化的影响,提出了横向距离间隙量作为短裤截面的评价指标;王利等[10]同样基于此技术量化了连衣裙腰围和摆围形态与样板结构的关系等。说明三维扫描技术可以深度解析服装内空间形态[11],且能够多维度评价服装造型。但目前基于该技术的研究主要集中于服装局部造型评价或服装与人体横向截面间的距离关系,缺少对服装整体三维空间造型的量化分析。

故本文以受众面广且造型优美的斜裙为例,提出基于三维扫描技术的斜裙空间造型客观评价体系,包括纵、横向及整体的造型指标,研究样板结构与斜裙三维造型的关系,以期为服装造型领域提供更客观、精确的评判指标,同时也可为厘清样板结构与服装造型之间的关系提供借鉴。

1 实 验

1.1 斜裙样板设计

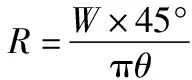
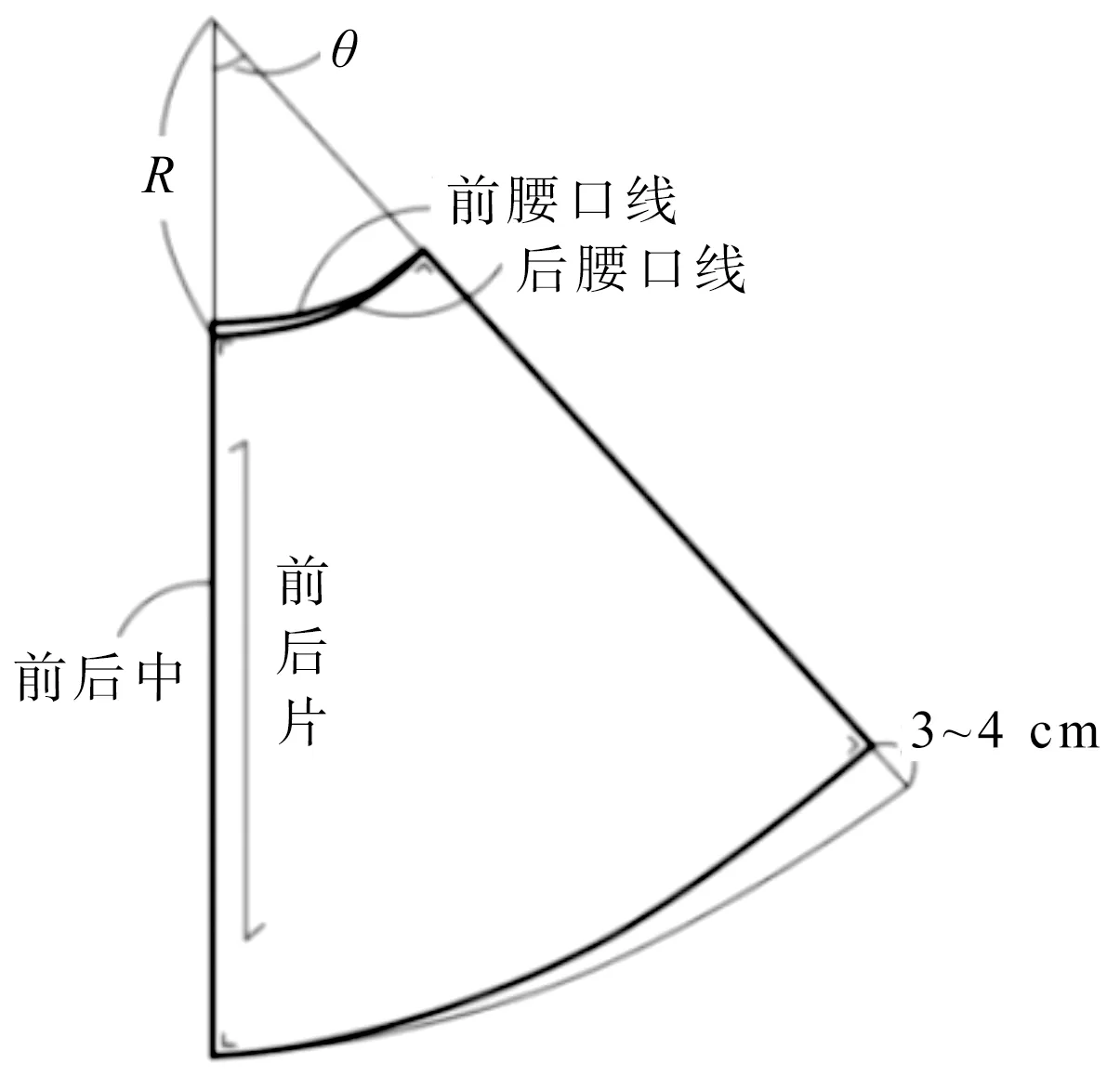
图1 斜裙样板Fig.1 Oblique skirt pattern

1.2 斜裙制作

由于本文仅研究样板结构对斜裙造型的影响,故基于单变量实验原则选择仅1种面料制作斜裙。市面上斜裙多用棉布、化纤、丝绸织物等裁制,在市场调研的20种斜裙面料中选择了一款悬垂性和抗皱性较好的化纤织物作为实验用料,织物规格如表1所示,并按照图1所示的样板制作6款不同θ的斜裙。

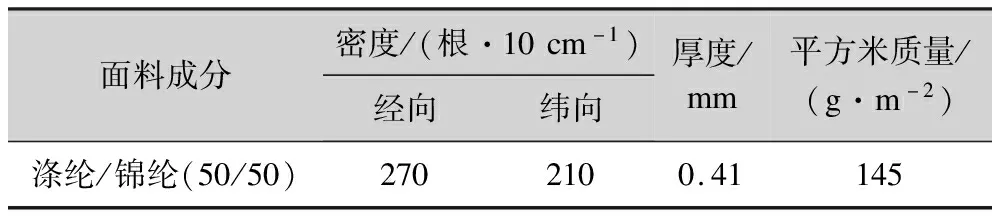
表1 织物规格Tab.1 Fabric specification

1.3 斜裙三维造型信息获取

1.3.1 三维扫描

采用EinScan Pro 2X Plus手持式多功能3D扫描仪(先临三维科技股份有限公司),扫描精度为0.045 mm,单片扫描范围为209 mm×160 mm～310 mm×240 mm,其原理是通过光的反射标定获取斜裙的空间造型信息。为避免实验误差,利用同一台扫描仪对1件样裙扫描3次,共获取3×6=18组点云模型。扫描时样裙穿在腰围66 cm、臀围90 cm的标准人台上,并使裙腰在人台腰线上方、腰头下缘线与人台腰线平齐、裙身左右侧缝线对称,穿着状态平衡且稳定。

1.3.2 点云预处理

由于原始的点云数据体量大且存在冗余噪点,不利于后续处理,故利用逆向工程软件IMAGEWARE 13.0进行去噪及精简处理,降低点云数据量。此外由于扫描仪的自定位技术不同于IMAGEWARE软件,需对人台进行坐标系重构：创建人台腰围的点云截面,在腰围特征截面的中心点O处创建新坐标系,人台竖直方向为Z轴,厚度和宽度方向分别为X轴和Y轴,再基于特征截面进行新旧坐标系重合处理,达到最佳拟合后,即得到重构后的人台空间坐标系,如图2(a)所示。样裙的扫描仪空间坐标系如图2(b)所示。为统一18个斜裙点云的空间坐标系,需对着装人台与裸体人台的点云模型进行对齐,将扫描的样裙模型完全重合到重构坐标系后的人台模型上,得到对齐后的样裙空间坐标系,如图2(c)所示。

图2 空间坐标系Fig.2 Coordinate system alignment

另外还需对样裙模型进行区域裁断,去除腰线以上及裙摆变形产生的参差部位。以Z=0 cm和Z=-54 cm的平面对样裙模型进行裁断,将所有的模型都限定在XYZ空间的有界区域中。

1.4 斜裙三维造型指标提取

对预处理后的18组斜裙点云模型进行空间造型指标提取,分析斜裙的整体造型、径向波褶造型及横向截面造型等特征。

1.4.1 整体造型指标

利用体积V与表面积S反映斜裙造型的体量感和立体度。为精确测量这两者,对点云模型进行三角网格面化处理,如图3所示。利用针对三角网格模型的【评估】工具获取由网格面域化的曲面面积S及面域包容的三维空间总量V。

1.4.2 纵向造型指标

(1)

(2)

(3)

(4)

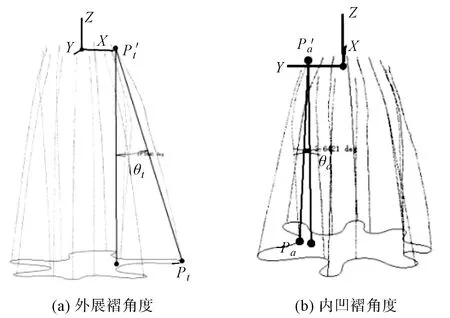
图4 波褶径向造型参数Fig.4 Radial modeling parameters of wave pleat

1.4.3 横向造型指标

在Imageware软件中通过【平面点云截面】工具,对点云模型Z轴负方向以XOY平面截取特征截面点云层Lk,k取值[0,9,18,27,36,45,54],代表截面层距腰线的距离。其中,L0为腰围截面层,L9为腹围截面层,L18为臀围截面层,L27、L36、L45分别为裙身截面层,L54为裙摆截面层。

通过截面点云数据构建4阶自由曲面,得到曲线轮廓最小外接矩形,如图5所示。并在软件中提取各截面层最小外接矩形的宽度Wk、厚度Tk及曲线截面面积Sk。

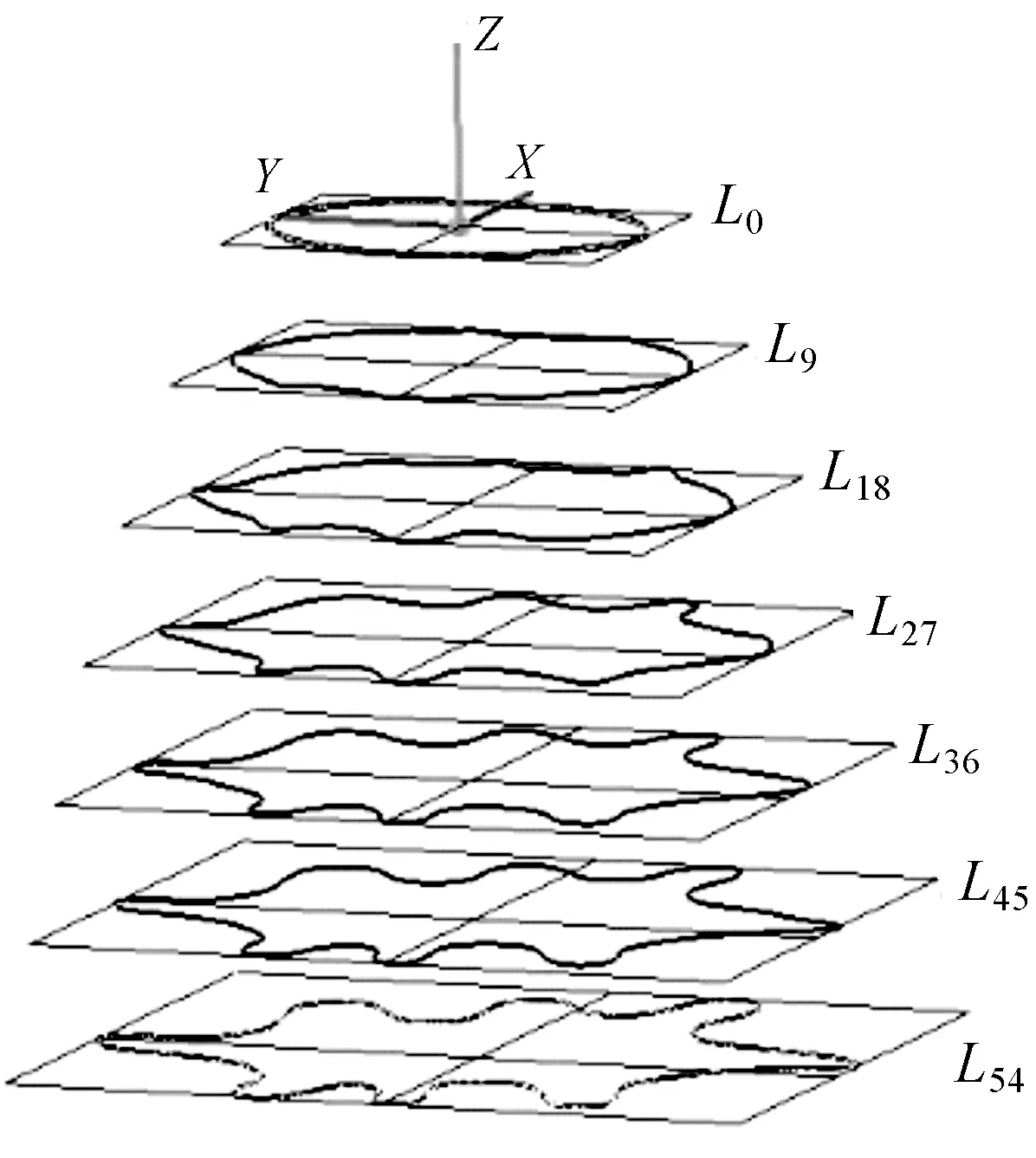
图5 曲线轮廓最小外接矩形Fig.5 Minimum circumscribed rectangle of curve contour

由于固定了腰围尺寸,当斜裙穿在人台上时,腰线紧贴人台,对斜裙整体造型影响不大,因此本文仅以斜裙点云模型的腹围、臀围及摆围截面作为研究对象,并以截面饱满度和椭圆度作为评价截面廓形的指标。

1) 饱满度δ。指截面面积与最小外接矩形面积的比值,用来表征截面的形状特征,取值范围0～1。值越小说明截面曲线的凹凸越明显,值越大说明截面廓形越饱满,计算公式如下：

(5)

2) 椭圆度σ。指截面宽度与厚度之比,用于表征截面形状。值越大说明截面越接近椭圆,值越小说明截面越接近圆形,计算公式如下：

(6)

2 结果与分析

2.1 相关分析

图6(a)显示了表面积S与样板角度θ的关系,可知两者呈显著相关性,随θ的增加,S呈逐渐增加的趋势。样板角度的增加会使得裙摆量增多,表面积故随之呈正比增大趋势。斜裙三维造型指标与θ的相关系数如表2所示。由表2可知,S与θ呈高度正相关,相关系数达0.988,而V与θ的相关性不显著。图6(b)显示V与θ存在非线性关系,V随θ的增加呈先增大后减小趋势,在θ=35°时V达到最大。随着裙摆量的增大,使得裙身可以包围的空间量增加,但由于受地球引力作用,原本较平整的面料在人台四周形成的起伏变大,裙面凹陷的部分变多,外鼓的空间变窄,导致裙身包围的空间反而有所降低。

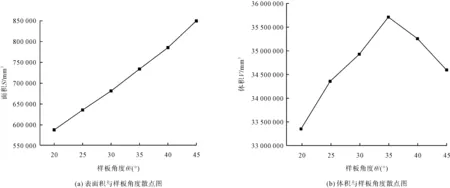
图6 整体造型指标与θ的散点图Fig.6 Scatter chart of overall shape index and θ

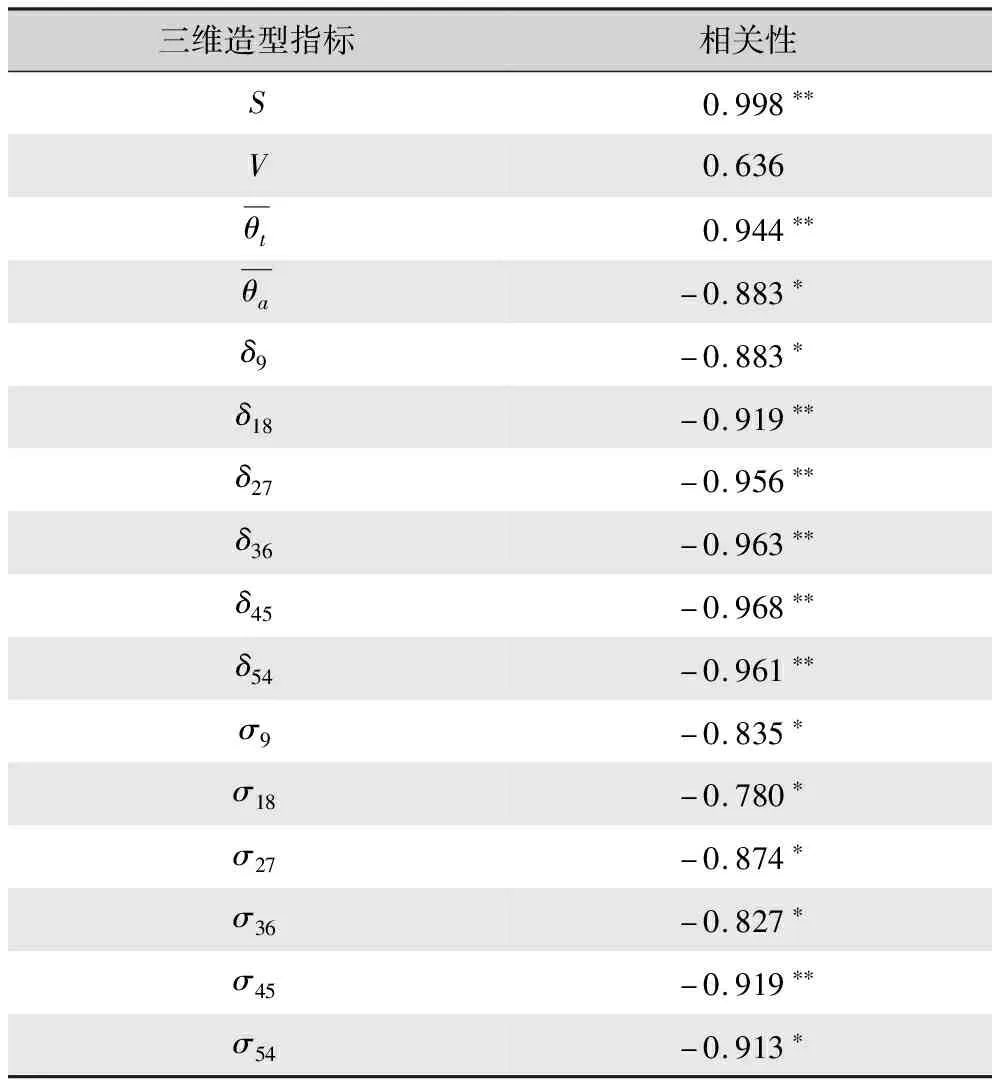
表2 三维造型指标与θ的相关系数Tab.2 Correlation coefficient between 3D modeling index and θ

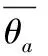
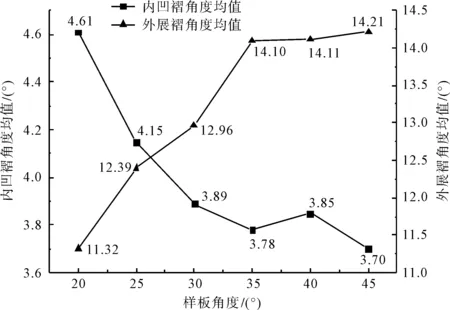
图7 径向波褶指标与θ的散点图Fig.7 Scatter chart of radial wave convolution and θ

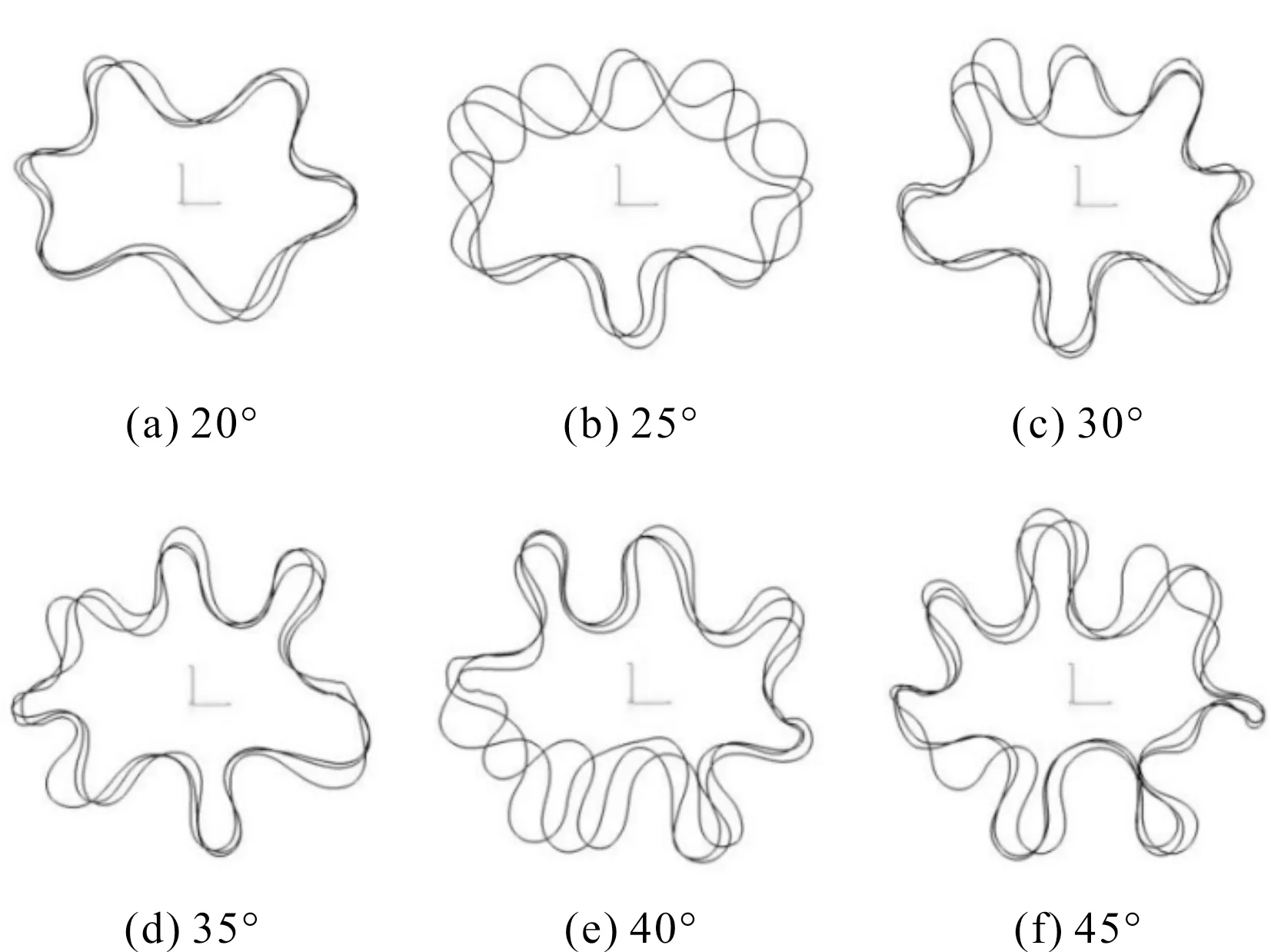
图8 不同θ时的斜裙裙摆截面Fig.8 Cross section of oblique skirt corresponding to different θ values

由表2饱满度、椭圆度与θ的相关系数可知,σ和δ与θ的相关性普遍高于-0.800,呈高度负相关。结合图8发现,随θ变大截面廓形由类椭圆形逐渐向类圆形靠近,即截面的σ逐渐变小。这是由于人台的臀部的凸势大于髋骨的凸势,面料在臀部堆积量变多,波褶外凸趋势增加,宽厚方向距离趋向一致,故截面椭圆度减小。δ随θ的变大而减小,当波浪间起伏程度变大,导致波谷的内凹幅度更甚,截面饱满度δ下降,变成近太阳花形状。

图9(a)为不同θ下的截面饱满度δ和椭圆度σ与截面层高的散点图。由图9(a)可知,从斜裙的腹围层向裙摆层逐渐变小,说明截面曲线的波浪起伏逐渐变大。其中θ=20°的斜裙,其各特征截面的σ和δ最高,即该角度下的斜裙截面最接近椭圆,最饱满。这是因为20°样板下的斜裙波浪较少,裙身最贴体,截面饱满且接近椭圆(图8(a))。

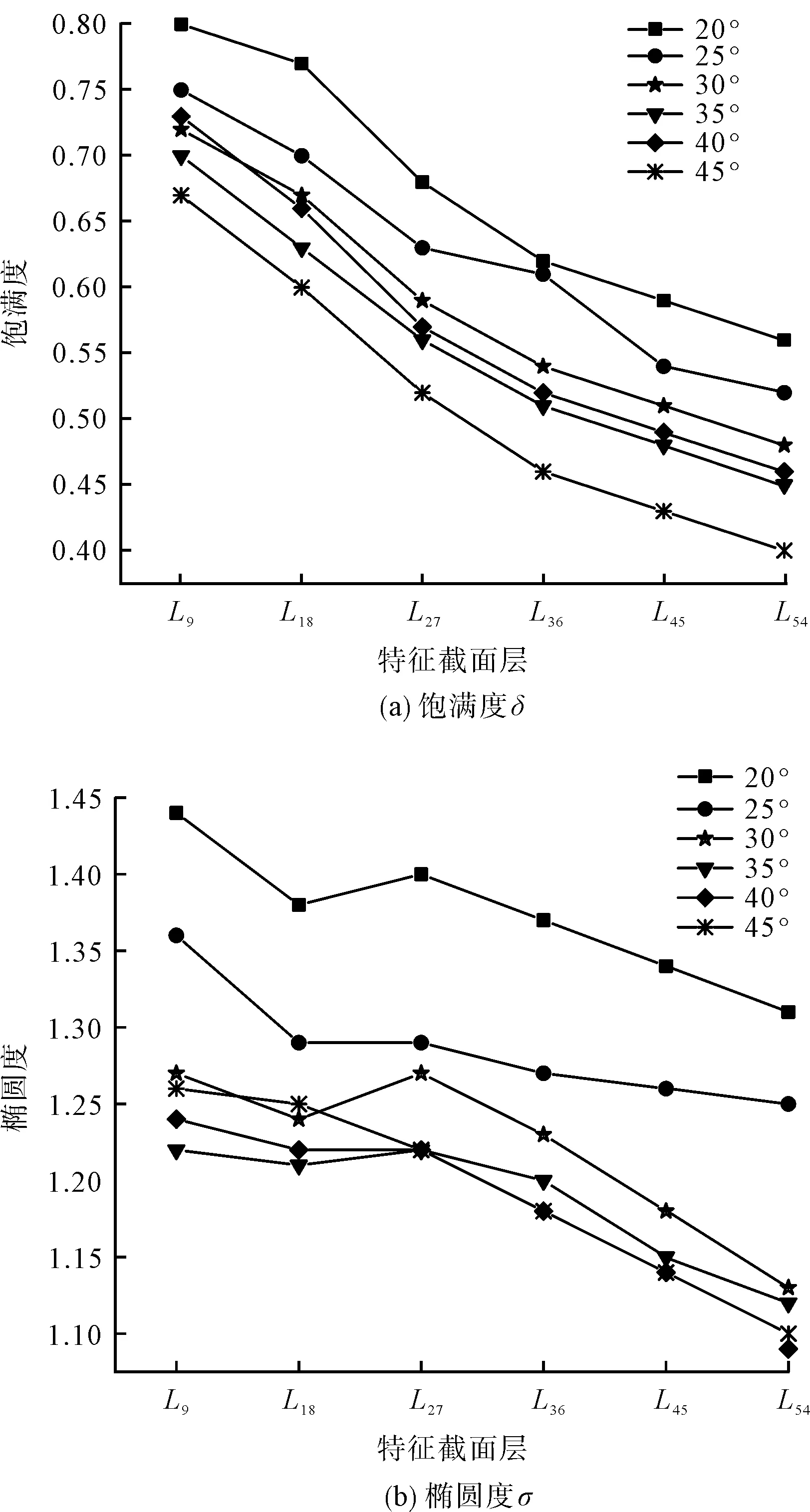
图9 不同θ时的σ和δ与特征截面的散点图Fig.9 Scatter diagram of characteristic section under different θ, σ and δ values

由图9(b)可知,当θ≤35°时,σ从斜裙腹围层到裙摆层大体呈现减—增—减的趋势,这是因为臀部脂肪较多,臀围截面廓形比腹围更接近圆形。在θ≤35°时,裙面在腹臀区域比较贴合人台,即截面廓形受人台的影响,使臀围椭圆度σ18<腹围椭圆度σ9;而L18以下,逐渐脱离臀部支撑,截面廓形回落呈近椭圆状;当θ>35°时,斜裙曲面起伏变大,截面廓形受人台影响减弱,σ呈逐层递减趋势。

2.2 回归分析

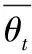
表3 三维造型指标与θ的回归方程(曲线估计)Tab.3 Regression equation of three-dimensional modeling index and θ (curve estimation)

由表3可知,除L36外,各特征截面层的椭圆度σ预测模型的拟合优度均优于饱满度δ。其中L9、L18、L45的σ预测模型的判定系数达0.970以上,拟合优度最好。L27、L36、L45、L54的δ预测模型的判定系数也都在0.900以上,拟合优度较好。

为进一步验证预测模型的准确性,本文重新制作θ=22.5°和θ=32.5°的斜裙进行验证,以三次扫描结果提取的三维造型指标原始值与模型预测值进行两配对样板T检验,结果如表4所示。由配对样本之间的均值标准误差可知,除V和S外,其余指标的实际值和预测值的均值、标准误差都小于1。

由于V和S的实际均值分别为3 4700 467.46和711 121.403 9,基数很大,故认为标准误差在可接受范围内。在显著性水平为0.05的情况下,T检验的统计量对应的显著性值均大于0.05,说明实际值和预测值无显著差异,进一步表明了基于θ的斜裙三维造型预测模型具有较高的准确性。

3 结 论

本文针对斜裙这一常见的女性服装展开研究,提出了一种基于三维扫描技术的斜裙造型客观评价方法。

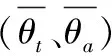
2) 以特征截面的椭圆度σ和饱满度δ来表征斜裙横向截面的廓形变化,研究发现各特征截面的σ和δ都与θ呈负相关,随θ的增加斜裙各围度截面曲线的起伏程度变大,波褶造型趋向细长,δ下降,同时截面宽厚方向的波褶起伏程度趋向一致,截面廓形更近似圆形,σ值变小。

3) 构建了基于样板角度θ的斜裙造型预测模型,该模型的拟合优度较高,利用θ=22.5°和θ=32.5°的斜裙三维造型指标进行预测值与实际值两配对样本T检验。结果表明实际值与预测值无显著差异,说明模型具有较高的准确性,同时证明利用三维扫描技术对服装造型进行客观评价具有良好的可行性。

《丝绸》官网下载

中国知网下载