深度教育理念下初中数学课堂教学策略研究

韩国燕

【摘要】在如今的初中教育中，培养学生的数学核心素养始终被强调，并在初中数学教师的教学改革创新中持续深化.多数教师与学者都一致认同深度学习是培养学生数学核心素养的“捷径”.而学生的深度学习则依托于教师的深度教育.鉴于此，文章从深度教育理念出发，对指向中学生数学核心素养发展的数学课堂教学提出了以情境教学催动深度学习，锻炼数学运算能力；以探索教学助力精准学习，发展逻辑推理能力；以数形结合促进有效学习，深化课堂学习体验；以生活教学推动高效学习，培养学以致用能力这几条策略，旨在提高初中数学课堂教学效率.

【关键词】深度教育；初中数学；数学教学；课堂教学；教学策略

基于深度教育理念创新改革初中数学课堂教学，不仅能够有效优化初中数学教学组织形式，革新应试教育观所造就的固化教学格局，促成高效初中数学课堂的构建，而且对学生数学核心素养的提升与当代初中教师专业化发展有着不可小觑的重要影响与积极作用.因此，为了更好地促进立德树人根本教育任务的落实，身为新时代教育工作者的初中数学教师必须在深度教育理念的指引下积极探索与实践有效推动学生深度学习的课堂教学策略，以此来更好地助力学生的终身发展.

一、以情境教学催动深度学习，锻炼数学运算能力

在当前的初中学校教育中，情境教学有着极为广泛的应用，既能够革新教学形式，活跃课堂教学气氛，也能够有效激活学生的学习兴趣，提升学生的课堂参与度.由此，初中数学教师可将情境教学应用到学生数学运算学习之中，为枯燥、乏味的数学课堂赋予生命力，从而在有效削弱数学运算难度与抽象性的同时，让学生在情境的作用下更为迅速、更为精准地发现数学运算的规律与技巧，进而爱上数学，为学生后续深度学习的实现夯实基础.

如，在“有理数的乘除法”一课的教学中，教师就可利用多媒体设备为学生展示登山队伍攀登珠穆朗玛峰的纪录片，以此来为学生创设教学情境，将学生的注意力有效集中到数学课堂上，并结合户外温度计的情境图向学生提问：“人们一般都使用正负数表示气温的变化，上升为正，下降为负.这支登山队伍在攀登珠穆朗玛峰时，发现每登高1km，气温变化量为-8℃.如果这支登山队伍登高4km，气温会有什么变化？”根据已知的有理数加减法与四则混合运算知识，学生便能够很快地列出算式“-8×4=”，但在具体的计算中，学生往往会得出“-32℃”与“32℃”两种截然不同的答案.对此，初中数学教师可从学生实际生活入手，引导学生思考：“在冬天，如果在下午14：00气温为8℃，氣温每小时下降1℃，那么在傍晚19：00时，气温变化了多少度？是几度？”在这一过程中，教师应将语气着重放在“变化”二字上，让学生主动联系有理数的加减法展开数学运算，即可得出算式：（19-14）×1=5℃，所以气温变化了-5℃，19：00时气温为+8+（-5）=3（℃）.由此学生便会受到启发，认识到在有理数乘法中，正数与负数相乘时积是负数，正数与正数相乘时积为正数，从而确定出上述问题的答案为-32℃.在此基础上，教师还可针对学生思维的发散点为学生提供乘法算式，让学生计算下面几组算式，并以小组合作的形式总结有理数乘法的运算规律.

在对以上几组简单的算式进行计算后，学生便会自觉地归纳出有理数乘法的法则：两数相乘时，需先确定积的符号，同号为正，异号为负，最后把两数的绝对值相乘，即可得出有理数乘法的积；任何数与0相乘都为0.

“有理数”的运算是初中数学教学中的基础内容，对学生后续的数学学习起着极为关键的奠基作用.将情境教学融入这一部分的教学之中，不仅能够有效削弱有理数运算的枯燥性、乏味性，增强学生的数学学习兴趣，锻炼学生的数学运算能力，还可以让学生在具体情境的催化下对数学知识的实用价值形成正确认识，其数学学习态度与情绪便会因此而得到端正，深度学习也会就此发生.

二、以探索教学助力精准学习，发展逻辑推理能力

逻辑推理是学生学习数学必备的思维能力.但初中生的认知水平与思维能力尚处于发展阶段，这就使得学生在实际的数学学习中很难自觉、主动地展开对数学知识、问题的探究.因此，为了让学生有效摆脱学习依赖心理，得到数学思维的活跃与发散，初中数学教师可应用探索教学法引领学生展开数学探索分析，通过精心设计教学问题的方式驱动学生，让学生的逻辑推理能力在分析问题、探究问题、解决问题的过程中得到提升与锻炼.

如，在教学“平行线及其判定”一课时，教师就可在学生从平行四边形、长方形、梯形等几何图形中初步掌握与认识“在同一平面内两条不相交的直线是平行线”这一平行线定义后，向学生提问：“直线、线段与射线有什么特点？”让学生主动联系已知分析出直线无限延伸的图形特点，从而主动对平行线的判定方法发出质疑：“直线是无限延伸的，仅以两条直线不相交就定义两条线是平行线是否不够精准？有没有更为准确的方法判定平行线？”之后，教师就可针对学生的这一求知需求，以问题引领学生展开对平行线三种判定方法的探索学习.

【判定方法1】同位角相等，两直线平行

教师利用多媒体设备为学生展示木工用角尺画平行线的情境，并向学生发问：“你认为木工用角尺画平行线的道理是什么？”让学生在问题的驱使下，利用数形结合的思想方法进行探究与分析，进而得出“两条直线被第三条直线所截，同位角相等，两直线平行”的结论.

【判定方法2】内错角相等，两直线平行

以学生自主得出的“同位角相等，两直线平行”结论为引，为学生展示a，b两条直线被直线c所截得到的图形（如图1），并让学生说出图中的∠1，∠2，∠3，∠4分别是什么角，分析如果∠2=∠3，是否能够判定a，b两条直线是平行线.

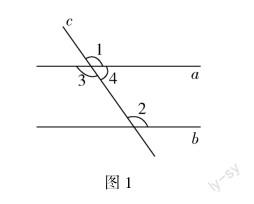
在探索这一问题的过程中，学生便会根据已知的“角”知识说出∠1和∠2为同位角，∠2和∠3为内错角、∠2和∠4为同旁内角.并结合【判定方法1】中的“同位角相等，两直线平行”结论对“如果∠2=∠3，是否能够判定a，b两条直线是平行线”这一问题进行验证与分析：

∵∠3=∠1（两直线相交，对顶角相等），

又∠2=∠3，

∴∠1=∠2，

∴a，b两条直线是平行线（同位角相等，两直线平行）.

由此便可得出结论：内错角相等，两直线平行.

【判定方法3】同旁内角互补，两直线平行

在学生得出“同位角相等，两直线平行；内错角相等，两直线平行”两种平行线判定方法后，教师便可提问：“除了以上两种方法，你们还能够根据哪些角的知识判定两条直线平行？”让学生结合图1中的几种角展开对问题的探索与分析，通过假设“∠2+∠4=180°”的方式，推出第三种平行线判定方法，即“同旁内角互补，两直线平行”.

以问题驱动学生展开对数学知识的探索分析、对数学规律的推理归纳、对数学问题的分析探究，不仅能让学生得到数学学习潜力的开发、数学思维的发散，还能够让学生的数学学习实现纵深发展，促成学生逻辑推理能力的提高.

三、以数形结合促进有效学习，深化课堂学习体验

数形结合是初中数学教学中应用频率极高的数学思想方法.无论是最为基础的有理数运算，还是难度较高的“求动点”问题都有数形结合思想的身影.因此，在有效促进学生深度学习的同时，为了让学生的数学解题能力得到更好的锻炼，在建设高效数学课堂的过程中，初中数学教师也可向学生积极渗透数形结合思想，让学生在抽象的“数”与直观的“形”的交互作用下得到数学学习体验的深化，实现数学核心素养的发展.

如，在教学“点和圆、直线和圆的位置关系”一课中，教师就可利用数形结合思想引导学生对点和圆、直线和圆的三种位置关系进行讨论分析.

首先，对点和圆位置关系的探讨.教师可为学生绘制图形（如图2），让学生结合图形对A，B，C三点与☉O的位置关系进行讨论：设☉O的半径为r，由图可知点A在圆内，OAr.点和圆的三种位置关系便由此得到明晰.

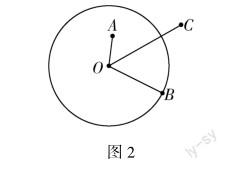
其次，对直线和圆位置关系的探讨.教师可利用多媒体设备为学生展示“海上日出”的美丽景色，让学生从海平面与太阳两个具体事物中抽象出直线与圆两个图形，自主绘制出直线和圆的三种位置关系图（如图3）.设直线l到圆心的距离为d，☉O的半径为r，分析d与r的数量关系，便可梳理出直线与圆的三种位置关系，即：dr，直线与圆相离.

最后，对圆和圆位置關系的探讨.教师可让学生以小组合作的形式根据点与圆、直线与圆的位置关系对两个半径不同的圆O1和O2可能出现的位置情况展开探究分析，并运用数形结合思想绘制出圆O1，O2的位置关系图（如图4）.设O1，O2两圆心的距离为d，圆O1的半径为r1、圆O2的半径为r2.通过分析d与r1，r2的数量关系，便可归纳总结出两圆的位置关系（表1）.

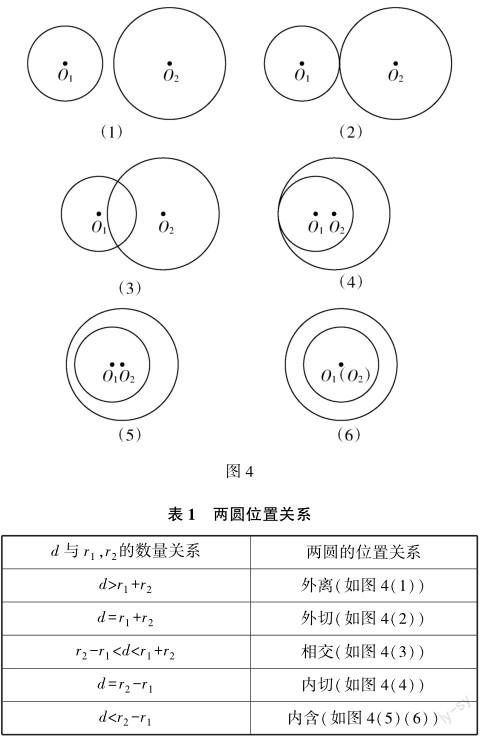
数形结合思想方法在初中数学教学中的渗透与运用能够有效激活学生的思维，深化学生的数学学习体验，促成学生的深度学习.在这一基础上，初中数学教师还可巧妙灵活地运用微课、希沃白板等信息化教学技术对教学进行合理的优化改良，以此来更好地发挥数形结合思想在促进学生学习、活化学生思维上的突出作用，推动学生数学核心素养的稳定发展.

四、以生活教学推动高效学习，培养学以致用能力

数学是一门与学生实际生活有着密切联系的学科.《义务教育数学课程标准（2022年版）》所提出的核心素养育人任务，也将学生的实践能力与学以致用能力的培养放在首要位置上.因此，在基于深度教育理念引导学生展开深度学习时，初中数学教师也要秉承着生活化教学思想，将学生的实际生活引入初中数学教学中来，为学生打造更为真实、具体、形象的生活化场景，让学生在应用数学知识解决实际生活问题的过程中，实现浅层学习到深度学习的过渡，得到思维能力的进阶与学以致用能力的发展.

如，在教学“二元一次方程组”一课时，教师就可从学生实际生活入手，根据当代中学生熟知的“淘宝双十一活动”进行编题，从而在有效激活与调动学生解决数学问题的兴趣的同时，让学生在分析与探究实际问题的过程中，形成良好的数学应用意识.

问题：在“双十一”前，学校在网上购买过两次教学物资.第一次，买了80个盒装粉笔和30个黑板擦；第二次以相同单价，买了50个盒装粉笔和20个黑板擦.第一次用了450元，第二次用了285元.在“双十一”大促期间，学校以活动价采购了1000个盒装粉笔和500个黑板擦，一共用了5250元，此次购买比“双十一”前购买少花了多少钱？

面对如此新颖且与自身实际生活紧密相关的数学问题，学生的学习兴趣与积极性会被充分调动起来，从而自觉主动地联系生活经验与二元一次方程组数学知识进行解题.如此，学生不仅会在解题中掌握更多二元一次方程的解法，得到数学思维的活跃与发散，其在分析实际生活问题的过程中，也会对数学知识的应用价值与魅力形成更为深刻、全面的认识与领会.在现实生活中，学生便会主动从数学学科的视角出发，运用数学思维与方法去尝试解决实际问题，理性分析.这不仅有利于学生深度学习的实现，对学生数学核心素养的发展提升也有着突出的促进作用.

总 结

总而言之，深度教育理念提出至今，已有很多学校在其引领下取得了卓越的成就.因此，可以说，深度教育理念能够切实地为现代初中数学教育的创新发展与现代化进步提供明确方向.所以，被誉为人类灵魂工程师的初中数学教师，必须认识到自身在新时期下所肩负的教书育人责任，并踏实、细致地履行教师的义务与使命，持续不断地探索与实践更具针对性的教学手段与方法，以此来更好地引导学生从浅层学习过渡到深度学习，从低阶思维进阶到高阶思维，助力学生数学核心素养的进一步提升.

【参考文献】

[1]管忠孝.深度学习视角下初中数学翻转课堂教学策略[J].家长，2021（32）：30-31.

[2]苏志华.初中数学教育现状及课堂教学策略探析[J].试题与研究，2020（12）：194.

[3]吕亚军.深度学习视阈下的初中数学课堂教学策略探析———一节省级重点课题研讨课引发的思考[J].中学数学月刊，2020（03）：27-30.

[4]赵文.现代教育视域下初中数学课堂的教学策略[J].数学大世界（中旬），2020（01）：87，86.

[5]李洁.深度学习视角下初中数学翻转课堂教学策略探究———以“解一元二次方程”为例[J].数学教学通讯，2019（29）：51-52，67.