基于核心素养的初中数学教学中学生审题能力的培养

倪鸿儒

【摘要】审题是解题的第一步，也是解决问题的最关键一步.一旦审题环节出现问题，学生的解题思路就会被扰乱，最终难以解得问题的正确答案.研究培养初中生审题能力的教学策略，对于提高学生的解题能力，促进学生综合发展有着积极意义.文章从核心素养的角度出发，对初中数学审题能力培养教学应秉承的原则进行了深入分析，同时综合实际教学案例指出教师可以通过呈现数学例题、讲解审题方法、创新审题教学模式、组织多元练习培养学生的审题意识，发展学生的审题思维，希望为提升初中数学审题教学质量提供参考.

【关键词】初中数学；核心素养；审题能力；培养策略

《义务教育数学课程标准（2022年版）》提出初中数学教学要以培养学生的数学学科核心素养、提高学生的数学综合应用能力为重点.此背景下，初中数学解题教学不应再以解题原理、解题方法的灌输为重点，应更注重培养学生的数学审题能力.同时，审题能力的培养教学要与数学抽象、数学运算、直观想象等核心素养的培养教学相关联，如此才能切实提高学生的题目分析、数学推理、数学论证、运算解题的能力，提升其审题水平.

一、核心素养下初中数学审题能力培养教学原则

（一）目标明确原则

教学目标指向不明会给教师的高效教学造成困扰，最终影响课程的教学效果.只有坚定教学目标，并围绕教学目标落实数学基础知识、数学基本方法、数学思想教学工作，才能够加深学生对数学教学内容的体会，为学生解题能力的形成与发展奠定坚实的基础.为此，教师应在实际教学中秉承目标明确原则，根据这一教学原则先确定课程教学目标、审题能力培养目标、核心素养培养目标，再基于初中生的具體情况融合三项教学目标，为教学工作的顺利展开指明方向.

（二）过程趣味原则

良好的教学体验感可以提升学生的数学探索内驱力，使其主动地参与数学问题分析、数学问题推理、数学问题猜想等教学活动，在潜移默化中培养学生的数感，提高学生的逻辑分析、数学抽象等思维能力.要想使初中数学审题教学达到理想的教学目标，教师就需要专注于教学过程的优化工作.同时，初中阶段的学生容易被趣味事物吸引，并对感兴趣的事物抱有极强的专注力.为此，教师应将过程趣味原则作为审题能力培养教学的主要原则，积极在课程中组织趣味情境、趣味探究、趣味互动教学活动，驱动学生在趣味活动中感受数学原理，探究数学问题，在提升学生核心素养水平的同时促进其审题能力的生成与发展.

（三）内容严谨原则

审题是一个严谨的过程，需要归类整理题目中给出的信息，需要挖掘题目中未点明的隐藏信息，需要根据信息确定题目主要求的是什么，要怎么解决问题.在某种程度上，审题能力的培养教学也可以看作判断能力、分析能力、抽象能力、逻辑能力、联想能力等多种能力的培养教学.在审题能力培养教学过程中，教师做出含糊判断、给出不明确的指导等教学行为都会打乱学生原有的审题思路，继而影响学生审题能力的形成与发展.为此，教师应秉承内容严谨原则开展教学工作，不仅要确保题目的严谨性，还要保证教学概念、思想方法的严谨性，以免学生受到错误信息的干扰，影响审题意识、审题思维的形成与发展.

二、核心素养下初中数学审题能力培养教学策略分析

（一）呈现优质数学例题，增强学生审题感知

题感指的是读题后能快速、准确地想到解题突破口的一种能力.培养初中学生的良好题感，对于提高学生审题能力有着积极意义.然而，题感的培养无法靠知识的灌输实现.教师应当为学生提供更多自主学习、自主练习的机会，让学生接触更多数学问题，使其在看不同问题、思考不同问题的过程中体会不同题目的审题方法，从而增强学生的审题感知.为此，教师可以应用多媒体课件、微课视频等信息化教学工具为学生呈现更多优质的数学例题，在拓宽学生习题视野的同时为提升其审题能力奠定基础.

以新人教版七年级数学上册“解一元一次方程（一）———合并同类项与移项”一课的教学为例，教师可以为学生呈现不同类型的数学习题：

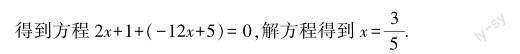
组织学生结合答案反思例题，使其在读题、读答案的过程中感知题目已知信息与题目所求内容之间的深刻关联，让学生在阅读更多例题的过程中积累更多读题经验，从而形成良好的审题感知能力.

（二）针对性讲解审题方法，提高数学审题效率

1.讲解关键信息提取方法，树立数据观念

数据观念的培养以客观认识数据的意义、体会数据中蕴含的关键信息为重点，注重锻炼学生收集数据、整理数据、分析数据的能力.数据观念的培养教学与审题能力的培养教学存在千丝万缕的关系.解题教学时，教师可以针对具体例题组织学生提炼题目信息，让其在自主尝试的过程中明确自身在数据整理、数据提取方面的发展不足.接着，教师再为学生系统地讲述提取题目关键信息的方法，之后组织学生进行实际演练，让学生在尝试、听讲、实操的过程中形成良好的数据观念.

以新人教版七年级数学下册“三元一次方程组的解法”一课的教学为例，有问题如下：“一个三位数，它本身是它各位数字和的27倍.现有如下信息：十位数字比百位数字、个位数字的和小1.如果将这个三位数的百位数字与个位数字交换位置，得到的新的三位数比之前这个数大99，那么原来的三位数是多少？”呈现例题后，教师可以提出指导问题：“这一题目都给出了哪些条件？你能从中获取哪些有用的信息？”借由问题激发学生的探究意识.之后，教师再为学生讲解提取关键信息的方法，如：审题要从问题着手，先将与题目有关的信息圈出来；审题要从条件与条件之间的关联着手，如不同条件之间的等量关系、已知条件与未知条件的关系等.如此，让学生在审题过程中明确这个三位数不同数位数字之间的相互关联，并根据题目给出的条件确定解题思路：

至此，学生经历了阅读数学问题、提炼关键信息、根据关键信息确定解题思路的审题步骤，能够在此过程中总结提炼解题关键信息的方法与技巧，其审题能力自然得到提升.

2.讲解隐藏条件挖掘方法，提升抽象素养

挖掘数学问题的隐藏条件是审题的关键环节.审题时，一旦忽略题目中的隐藏信息，就会影响学生解题思路的确定，数学运算的准确性，最终影响解题质量.然而，在目前的初中数学解题教学中，很多学生未能认识到挖掘题目隐藏信息的重要性，经常根据题目中直观的信息盲目解题.核心素养背景下，教师可以将抽象素养培养教学与审题教学有机结合，在指导学生探析问题的过程中引导学生挖掘隐藏条件，以免学生思考问题不全面，影响审题质量.

以新人教版八年级数学上册“三角形全等的判定”一课的教学为例，有问题如下：“中午12点时，操场上垂直于地面竖立着两根一样长的竹竿，它们的影长相等吗？”这一问题的提问方式比较隐晦，给出的表面信息也非常少.很多学生在接触这一问题时，完全不理解这一问题问的是什么，也不能从问题中提炼出解题的关键信息.这时，教师应为学生讲解挖掘题目隐藏条件的方法，如：题目信息一般隐藏在“垂直”“竖立”等关键词中，要根据关键词确定解题信息；题目信息可能隐藏在客观规律中，要结合生活实际挖掘解题信息，等等.通过引导，让学生挖掘以下隐藏条件：

（1）两只竹竿垂直地面竖立，竹竿与地面所成夹角为90°；

（2）太阳光线可以看成是平行的.

由这两条隐藏条件，可以分别将两条垂直地面竖立的竹竿、地面、斜射的太阳光线构建成两个直角三角形.这样，学生再根据隐藏条件求解问题，即可得到正确答案.

挖掘数学题目中的隐藏信息需要正确的方式方法.教师应当承担其教学指导、教学管理责任，在学生缺乏审题头绪时为其讲解挖掘隐藏信息的方法，使学生在学习方法、实际演练的过程中逐渐掌握挖掘题目隐藏信息的关键技能.

（三）创新解题教学模式，发展数学审题思维

1.“问题链”教学指导审题，培养逻辑推理素养

读题不完全等于审题.读题只是概括性地了解题目的信息，审题则是在读题的基础上分析题目给出的已知信息之间的关联，分析题目中已知信息与所求对象的联系.由此可见，高效审题是建立在良好的逻辑推理能力基础之上的.教师可以将“问题链”教学法应用到审题教学当中，借助“问题链”为学生搭建逻辑思考、深度推理的学习平台，驱动学生从数学的角度思考问题中蕴藏的逻辑，在锻炼学生逻辑思维的同时，进一步提升学生的审题能力.

这样，学生能够在分析问题结构、探析问题所考查的主要知识点、根据审题思路解决问题的过程中形成良好的逻辑推理思维，其审题能力自然得到提升.

2.“开放式”教学指导审题，增强数学创新意识

创新意识属于初中数学核心素养的一部分.将创新意识培养教学融入审题教学当中，对于发散学生审题思维，提升学生举一反三的审题能力有着积极意义.在解决一些类型独特、形式新颖、复杂程度较高的数学问题时，教师可以将“开放式”教学用于审题指导过程，通过给予恰当点拨为学生提供更多数学探索的灵感，让学生在猜想、假设、推理、验证的过程中确定不同的解题思路，从而培养学生的创新审题能力.

以新人教版八年级数学下册“勾股定理”一课的教学为例，有问题如下：“直角三角形有两条边长分别为3与4，则第三条边的长度是多少？”这一问题并未直接给出题图，也没有明确指出长为3，4的两条边具体是哪两条边.这时，教师可以围绕原问题组织学生合作探究：“你在讀这一问题时想到了什么？”通过师生互动，让学生明确题目中的关键信息———“有两条边长分别为3与4”，在此基础上启发学生的不同审题思路.

思路1：在这一直角三角形中，斜边长为4，某一条直角边的边长为3；

思路2：在这一直角三角形中，两条直角边的边长分别为3与4.

这样，学生可以根据不同的审题思路确定问题的不同解法，解得直角三角形第三条边的边长可能为5也可能为7.这时，教师再为学生出示变式问题：已知△ABC，AB=17，AC=10，BC边上的高AD=8，则BC的长是多少？这一问题与例题十分相似，需要学生考虑两条边的不同情况.出示这一例题后，教师没有为学生提供审题指导，而是让学生凭借之前积累的审题经验分析问题，确定解题思路，进一步锻炼学生的迁移、创新、应用能力.

（四）组织多元迁移练习，锻炼数学审题能力

1.组织运算题审题练习，培养运算能力

运算能力不仅是指高效解决计算问题的能力，还包括分析运算对象、选择合适运算策略等多种能力.从运算能力的培养角度出发设计运算题审题练习，可以打破学生对运算练习的刻板印象，使学生从运算分析、正式运算、运算结果检验三个角度看待运算问题，从而提升学生的读题、析题、审题、解题能力.为此，教师可以结合学生的实际发展需要整合运算练习题，以审题训练为主、解题训练为辅，进一步锻炼学生的审题能力.

2.组织应用题审题练习，树立模型观念

模型观念是运用数学模型解决具体问题的一种解题观念.从模型观念的培养角度出发设计审题教学活动，有利于发展学生问题分析、关联建构、规律探析的审题思维，对于提升学生的审题能力有着正面帮助.教师可以综合课程教学需求、学生能力发展需求精选数学应用题，并在课上组织学生读题、审题，驱动学生在此过程中关联主要信息，建构数学模型，确定问题解决思路.

以新人教版九年级数学上册“实际问题与二次函数”一课的教学为例，有应用题如下：“友谊公园要建造圆形喷水池，在水池中央垂直于水面处安装一个柱子OA，O恰好在水面中心.OA=1.25m，由柱子顶端A处的喷头向外喷水，水流在各个方向沿形状相同的抛物线落下，为使水流形状较为漂亮，要求设计成水流在离OA距离为1米处达到水面最大高度2.25m.如果不考虑其他因素，那么水池的半径至少要多少米才能使喷出的水流不至于落到池外？”由于是应用题，本问题无用的介绍信息比较多.审题时，教师应让学生从抽象的角度分析问题，提炼题目的关键信息，如“O恰好在水面中心”“OA=1.25m”等，让学生分析题目条件之间蕴藏的等量关系.接着，教师指导学生结合问题联想二次函数的相关知识点，让学生根据题意绘制平面直角坐标系，确定A点坐标和B点坐标.同时，教师还应在审题教学中渗透模型思想，让学生利用具象的、直观的问题信息建构数学模型，继而确定解题思路，得到抛物线方程，为高效解题奠定基础.

结束语

综上所述，基于核心素养的初中数学教学应当树立明确的教学目标，确保教学过程生动有趣、教学内容科学有效.在此背景下，初中数学审题能力培养教学应当对原有的教学资源加以优化，同时基于初中生审题能力发展情况合理落实审题意识、审题思维、审题能力培养的教学方案，进一步培养学生提炼关键信息、挖掘隐含条件、确定解题思路的良好审题能力与数学核心素养.

【参考文献】

[1]马月霞.“讀”具慧眼 “题”意自现———浅谈初中生数学读题能力与读题习惯的培养对策[J].新课程，2022（41）：80-81.

[2]司王林.初中数学解题教学中学生审题能力提升研究[J].理科爱好者，2022（04）：81-83.

[3]李亚勋.初中数学审题能力的培养策略[J].数理天地（初中版），2022（13）：93-95.

[4]侯庆秋.正确审题———提高初中数学思维能力的有效路径[J].数理天地（初中版），2022（07）：92-94.

[5]陈琴.初中数学中学生审题、解题能力的指导[J].数学大世界（上旬），2022（04）：74-76.

[6]胡继霞.初中数学审题能力的培养[J].现代中学生（初中版），2022（04）：27-28.