一题多解“细”探究 巧构函数“觅”思路
——一道以函数为背景的不等式恒成立问题的多解法探究
李春林
(甘肃省天水市第九中学,甘肃 天水 741020)
以函数为背景的不等式证明或不等式恒成立问题,是高考的常考题型,尤其是近几年来,此类题目常常作为压轴题目出现在高考试卷中,这类问题具有极强的综合性和技巧性, 充分考查了数学抽象、数学建模、数学运算、逻辑推理等数学核心素养,突出理性思维,彰显选拔功能,提升学生的数学核心素养[1].在解决这类问题的过程中,欲证不等式f(x)>g(x),常需要构造函数求导、判断单调性、求最值等.学生解题的难点在于如何构造函数.本文以一道湖北名校联盟2023届高三5月适应性大联考第21题为例,归纳整理几种构造函数解证不等式的策略,以期抛砖引玉,与大家共同探讨.
1 试题呈现
题目已知函数f(x)=2ex-2,g(x)=x·lnx,证明:x>1时,f(x)>g(x).
2 试题分析

3 多解探究
视角1直接作差构造函数.
分析令h(x)=f(x)-g(x)(x>1),将问题转化为证明:x>1时,h(x)>0恒成立.
解法1令h(x)=f(x)-g(x) (x>1),
即h(x)=2ex-2-xlnx.
则h′(x)=2ex-2-1-xlnx.
令u(x)=h′(x)=2ex-2-1-lnx,

所以u′(x)在(1,+∞)上单调递增.
又u′(1)<0,u′(2)>0,
所以∃x0∈(1,2),u′(x0)=0.
所以x∈(1,x0)时,u′(x)<0,u(x)单调递减,x∈(x0,+∞)时,u′(x)>0,u(x)单调递增.
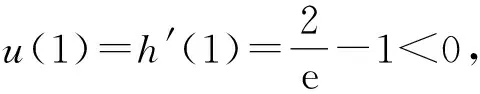
所以u(x0)=h′(x0)<0.
而u(2)=h′(2)>0,
所以∃x1∈(x0,2),u(x1)=h′(x1)=0.
即2ex1-2-1-lnx1=0.
故当x∈(x0,x1)时,h′(x)<0,h(x)单调递减,
当x∈(x1,+∞)时,h′(x)>0,h(x)单调递增.
所以h(x)≥h(x1)=2ex1-2-x1lnx1=1+lnx1-x1lnx1.
因为x1∈(x0,2),x0∈(1,2),
所以x1∈(1,2).
令V(x)=1+lnx-xlnx,x∈(1,2),
则h(x)≥V(x).
故V′(x) 所以V(x)在(1,2)内单调递减. 所以V(x)>V(2)=1+ln2-2ln2=1-ln2>0. 所以h(x)≥V(x)>0. 所以h(x)>0 . 即x>1时,f(x)>g(x) 得证. 点评通过直接作差构造函数h(x),将不等式问题转化为导数问题,通过研究h(x)的单调性、极值、最值等将问题加以解决. 视角2适当变形,再作差构造函数. 分析解法1虽然思路简单,但过程繁杂,继续探究后发现: 令u(x)=2ex-2·(x-1)-x, 所以u′(x)=2x·ex-2-1. 所以u′(x)在(1,+∞)单调递增. 所以∃x0∈(1,2),u′(x0)=0. 故当x∈(1,x0)时,u′(x)<0,u(x)单调递减, 当x∈(x0,+∞)时,u′(x)>0,u(x)单调递增. 又u(1)=-1<0,u(2)=0, 所以当x∈(1,2)时,h′(x)<0,h(x)单调递减, 当x∈(2,+∞)时,h′(x)>0,h(x)单调递增. 所以h(x)≥h(2)=1-ln2>0. 所以h(x)>0 . 即x>1时,f(x)>g(x)得证. 视角3直接作商构造函数. 令u(x)=xlnx-lnx-1(x>1),则 所以u(x)在(1,+∞)单调递增. 因为u(2)=ln2-1<0,u(e)=e-2>0, 所以∃x0∈(2,e),使得u(x0)=0. 即x0lnx0-lnx0-1=0. 所以x0lnx0=1+lnx0. 当x∈(1,x0)时,u(x)<0,h′(x)<0,h(x)单调递减,当x∈(x0,+∞)时,u(x)>0,h′(x)>0,h(x)单调递增. 所以V(x)在(2,e)内单调递增. 即 2ex-2>xlnx. 所以x>1时,f(x)>g(x) 得证. 视角4拆分不等式,构造双函数. 因为h(x)min>u(x)max, 所以h(x)>u(x)恒成立. 所以x>1时,f(x)>g(x)得证. 视角5 先放缩不等式,再构造函数. 解法5 先证明ex≥x+1. 令h(x)=ex-x-1,则h′(x)=ex-1. 所以h(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增. 所以h(x)≥h(0)=0. 所以ex≥x+1(当且仅当x=1时,取等号). 令h′(x)=0,得x=2. 显然h(x)min=h(2)=1-ln2>0. 所以x>1时,f(x)>g(x)得证. 所以xlnx≤x·ex-2>x·lnx. 所以x>1时f(x)>g(x)恒成立,得证. 问题是数学的心脏,一道好的试题,能够激发解题人的灵感,促使解题人展开想象,多角度审视,全方位思考,细致分析判断,从中挖掘问题的本质,从而探究出不同的解题思路与方法[2].纵观上述解法,虽然角度不同,方法各异,但解决问题的基本思路是相同的.即:①构造函数;②研究函数的性质;③运用函数性质解决不等式问题.而构造什么样的函数显然是解题的关键一环,这就要求我们在解题过程中,善于抓住题目特征,深入分析问题,找到已知与待求间的纽带.多视角、多方式变化思维形式,进行化归转化,将问题用另一种更为清晰的命题形式呈现出来.同时还要注意立足教材,夯实基础,学会总结归纳,分析解题思路,积累解题经验,抓住通性通法,让一题多解成为数学解题的常态[3].




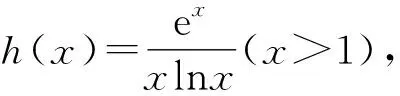
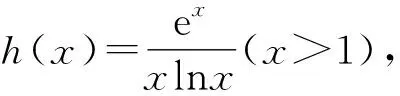
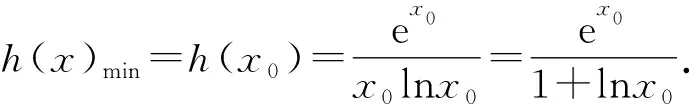




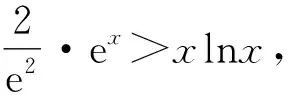












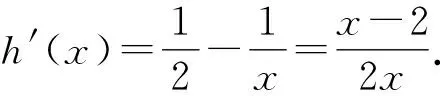








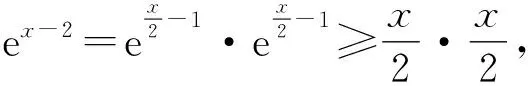
4 解后反思

