探究离心率问题的几何解法
梁启浩
(江苏省盐城中学,江苏 盐城 224008)
1 利用平量向量隐含的几何关系求离心率


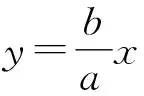

图1 例1解析图

结合渐近线的对称性得x轴平分∠NOP.
所以|ON|=|OP|.
所以ΔNOP是正三角形.

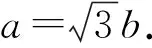
平方,得a2=3b2.
所以a2=3(a2-c2).

评注一般遇到平面向量我们都会考虑其大小和方向,而忽略其几何意义.新教材非常重视用平面向量研究几何问题,只有足够重视平面向量的几何功能,才能自觉形成数形结合思想,进而形成解题技巧,学生的发散思维才能得到培养.
2 利用三角形相似求离心率
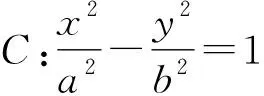
分析已知“以线段AF为直径的圆过点B”意味着∠ABF=90°,我们容易判断ΔOAB∽ΔOBF.利用此几何关系,可以得到关于a,b,c的代数关系式,进而求出离心率e.
解析如图2,设直线l与渐近线交于点E,因为以线段AF为直径的圆过点B,所以AB⊥BF.

图2 例2解析图
于是AB∥OE.
因此tan∠BAO=tan∠EOF.

所以|OB|=b.
因为∠BAO=∠EOF,∠ABO=∠AFB,
所以ΔOAB∽ΔOBF.
所以OB2=OA·OF.
即b2=ac.
于是c2-a2=ac.
所以e2-e-1=0.


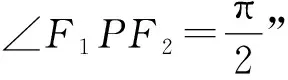
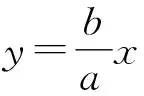

图3 例3解析图
那么∠ONF2=∠F1PF2=90°.
因为|OF2|=c,|NF2|=b,
所以|ON|=a.
由三角形相似知|PF1|=2a,|PF2|=2b.
由双曲线的定义知|PF2|-|PF1|=2a.
所以|PF2|=4a.
所以2b=4a.


分析如图4,本题中线条较多,让人眼花缭乱.但是也有了较多的三角形,我们可以去寻找与a,c相关的相似三角形,以便找到离心率的桥梁.不难发现|AF|=a-c,|BF|=a+c,于是瞅准△AFM和△AOE,△BFM和△BON,利用相似性三角形,可以顺利推进解答[2].
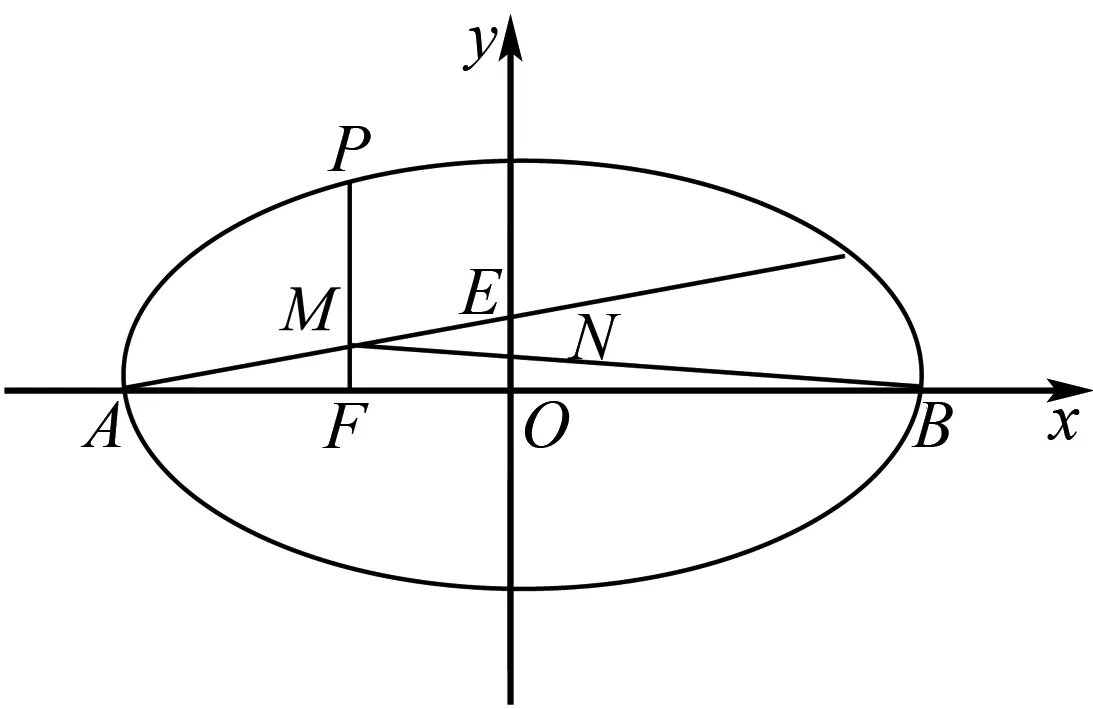
图4 例4解析图
解析由已知得△AFM∽△AOE.
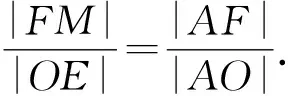

同理,△BFM∽△BON.

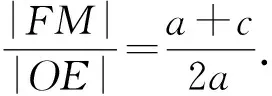

整理,得a=3c.
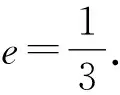

解析如图5,设点P关于y轴的对称点为P′,结合前文得P′(-a,b).

图5 例5解析图
同时,PP′∥OF1.
所以ΔQPP′∽ΔQOF1.
于是|PQ|∶|QF1|=|PP′|∶|OF1|.
因为|PQ|∶|QF1|=3∶2,
所以|PP′|∶|OF1|=2a∶c=3∶2,

评注圆锥曲线中的相似关系往往比较隐蔽,需要我们去发现,去挖掘,去利用.由直线间的垂直、平行关系表现出来的直线斜率关系(代数式)已经被学生熟知,甚至先入为主,遮蔽了强大的几何功能.解析几何的本质是几何,能够将解析几何问题的数量关系转化为几何位置关系,通常会大大降低运算量,使解题显得简洁明了.当然,这种转化还是很不容易的,以上几例如果用纯代数的方法计算,都比较繁杂,甚至可能找不到出口.因此,我们要主动往几何方向去思考,利用解析几何的几何本质属性,简化运算[3].
3 利用三角函数隐含的几何关系求离心率
分析例2中∠BFO,∠BFx的正切值均与a,b,c有直接或间接关系.在图2中,由于∠BFO+∠BFx=π,利用其互补关系,借助诱导公式,可以建立代数等式,我们也可以快速求解,此所谓“条条道路通罗马”.
另解例2 由上面解法知|OB|=b.

因为∠BFO+∠BFx=π,
所以tan∠BFO=-tan∠BFx.
因此tan∠BFO=-kBF.


以下同例2.
评注一些题目中的几何关系往往不止一种,我们只有在比较中才能发现最简洁的办法,思维不仅需从代数中跳出来,还要在几何领域中多角度、多方位去思考,方可让解析几何的几何属性充分暴露,为我所用.
4 利用切线关系求离心率

分析本题的已知元素比较丰富,直线、圆、椭圆都有了.位置关系比较复杂,直线和圆相切,圆和椭圆相切.椭圆、圆、圆的切线等知识融合在一个比较复杂的图形中,单纯从代数角度运算,问题不易解决.恰当利用切线性质构造一个正方形,再利用正方形中的数量关系以及椭圆和圆位置关系带来的数量关系,使问题暴露无遗,解法也简洁易行.
解析如图6所示,设切点为E,F,连接OE,OF,由平面几何知识可知|PE|=|PF|,OE⊥PE,OF⊥PF.

图6 例6解析图
所以四边形OEPF是边长为a的正方形.

评注本例充分显示了几何法求离心率的优越性.只要能发现几何关系,恰当应用几何关系,问题就会迎刃而解.
通过以上几例,我们都可以发现几何法求解离心率要比代数法简捷[4].我们应扭转思维,避免凡是解析几何问题都要硬算到底.几何法不仅可以简化运算,还可以提高准确率,同时可以开发学生的思维,锻炼学生一题多解,增强学生学习数学的兴趣,自觉探寻问题的本质,达到提升学生的数学核心素养的目的.

