高中物理解题中数学思想与方法应用举例分析
——以“三角函数”为例
孙志峰
(福建省惠安第一中学,福建 惠安 362100)
新时期,新的高考物理考试说明进一步明确了考生应用数学方法处理物理问题的能力的要求,高考生不仅需要在具体物理问题中找出物理量之间的数学关系,而且需要根据数学的特点与规律进行推导,并恰当运用几何图形、函数图像辅助物理判断、得出物理结论.因此,探究数学思想与方法在高中物理解题中的应用具有非常重要的意义.
1 高中物理解题中的数学思想
在高中物理问题求解中,可利用的数学思想与方法包括几何法、估算法、函数法、图解法、比值法、归纳法、微元法、极限分析法、特殊值法、分类讨论法、极值法等.其中在物理问题求解中应用频率较高的数学思想与方法包括函数图像、平面几何、数列、解三角形、不等式、微积分初步等[1].
2 物理解题中的数学“三角函数”思想与方法
2.1 三角函数定义
在高中物理问题求解中的“三角函数”思想与方法本质上是将角、比值分别作为自变量、函数值的函数,主要是:设a是一个任意角,a的正弦记为sina,a的余弦记为cosa,a的正切记为tana,a的余切记为cota,a的正割记为seca,a的余割记为csca[2].
2.2 三角函数定理
在高中阶段物理问题解析过程中,常用的三角函数定理主要包括正弦定理、余弦定理、正切定理等.其中正弦定理是三角函数基本定理,特指:对于任意一个平面三角形,其各边与边所对角的正弦值的比为同一数值,且各边与边所对角的正弦值的比等于外接圆的直径;余弦定理主要描述三角形中3边长度、1个角的余弦值的关系,即:对于任意一个三角形,任何1个边的平方等于其他2个边平方的和减去对应两边与其夹角的余弦的积的2倍;正切定理主要用于描述正切函数,即:一个三角形内,任意2条边的和除以第1条边减第2条边的差所得的商、两条边的对角的和的1/2的正切除以第1条边对角减第2条边对角的差的一半的正切所得的商是同一个数值.
3 高中物理解题中数学思想与方法应用举例分析——以“三角函数”为例
3.1 恒成立问题
借助三角函数思想方法解决物理恒成立问题,需要在分析题目物理过程、事物状态的情况下,根据物理规律列方程,再在方程中根据函数性质求解.在三角函数思想方法应用于物理问题解决过程中,最简单的用法是直接利用三角函数的正弦公式(或余弦公式、余切公式、正切公式求解).特别是在物理恒成立问题解析过程中,引导学生进行正交分解,联系列出式子直接利用三角函数求解.
例1一物体m放置在水平面上,m与水平面之间的动摩擦因数为μ,现施加一个斜向下的力F推物体,F与水平面之间夹角为φ.在m与水平面之间最大静摩擦力等于滑动摩擦力的情况下,φ至少为( )时,无论F多大均无法推动物体m.

3.2 物体的动态平衡问题
高中阶段,物体的动态平衡问题较为常见,特指物体自始至终处于平衡状态但受力持续发生变化的一类问题[3].一般情况下,物体的动态平衡问题多为3个力作用下的平衡问题,部分情况下物体的动态平衡问题也涉及4个力的平衡.解决上述问题一般需要根据平衡条件列出方程,由所列方程分析物体受力变化,即函数法,或者根据平衡条件绘制力的分解图(或合成图),在图像中分析力的变化,即图解法.根据不同方法的应用过程,教师可以引导高中生选择恰当的三角函数,辅助解决物体的动态平衡问题.
3.2.1 函数法解决物体的动态平衡问题
高中阶段,解决平衡问题的基本思路是分析受力,结合平衡条件(或三角形定则、三角函数定理)等知识进行解析.从函数解析视角来看,物体的动态平衡问题是通过控制特定物理量的变化促使物体整个状态发生缓慢变化,缓慢变化特指速度极小的变化,可认定为速度为0,此时,物体在变化阶段达到平衡状态.教师可以引导学生分析物体动态平衡条件,根据条件列方程,根据方程带领学生探究物体受力变化.
例2轻绳两端分别系在质量为m的物体上、轻质圆环上,圆环套在粗糙水平杆MN上,此时,利用水平力F拉动轻绳上一个节点,促使物体达到某一位置(图1中实线),进而变更水平力F的大小,在圆环位置一定的情况下,促使质量为m的物体连同轻绳下降(图1中虚线),在整个过程中,水平力F、圆环与粗糙水平杆MN的摩擦力Fm、圆环对粗糙水平杆MN的压力FN的变化情况是( ).

图1 例2示意图
A.F逐渐增大,Fm保持不变,FN逐渐增大;
B.F逐渐增大,Fm逐渐增大,FN保持不变;
C.F逐渐减小,Fm逐渐增大,FN逐渐减小;
D.F逐渐减小,Fm逐渐减小,FN保持不变.
解析上述题目为高中阶段典型的力的动态平衡问题,可以利用力的合成思想进行求解,同时需要利用数学知识中的三角函数知识进行解析,需要高中生熟练了解三角函数定理在物体动态平衡类物理问题中解析的规律[4].
答案:D
3.2.2 图解法解决物体的动态平衡问题
在基于图解法的力学题目解析过程中,三角函数思想应用的关键在于借助正交分解梳理问题解析思路,明确物体受力后构建直角坐标系,完成力的分解.进而根据牛顿运动定律,完成公式联列[5].在公式联列后,教师可以带领学生根据三角函数的性质进行问题解析.如例题2中,质量为m的物体在水平力F、物体重力、圆环与粗糙水平杆MN的摩擦力Fm的作用下处于平衡状态,水平力F与轻质绳的拉力FL的合力与重力平衡,表明水平力F与轻质绳的拉力FL的合力大小恒定,方向竖直向上,且水平力F的方向维持一定,根据力的三角形法则,可以水平力F与轻质绳的拉力FL的合力、水平力相互垂直,绘制矢量图(见图3).
3.3 运动规律问题
高中物理题目中,运动规律问题涉及了简谐运动、机械波运动等.在运动规律问题解析中需要运用三角函数的相关知识,如求解简谐运动的振动方程可以转化为利用三角函数图像求解三角函数解析式[6].
3.4 物理最值问题
作为函数的一种,三角函数在物理问题解析中的应用与一般函数类似,求解物理最值是三角函数应用的主要方面[7].

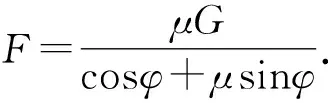
列出式子后,教师可以鼓励学生利用三角函数中的辅助角公式进行解决.即:
其中θ满足

在cosφ+μsinφ最大时,F最小.

综上所述,函数思想特指利用函数表示某一物理问题,借助函数的概念、性质进行物理问题的分析、转化与求解,并探明相关类型的一般规律.三角函数思想是重要的函数思想,教师应根据物理最值、恒成立、动态平衡等问题内容,带领学生借助三角函数思想逐步分析、求解,在帮助学生顺利解决物理问题的同时,提高学生跨学科学习能力.

