高考中的动点轨迹问题初探
张矩铭
(龙泉师一中学 ,四川 成都 610100)
“双新”背景下,新高考注重对数学本质的考查[1],而直线、圆和圆锥曲线的方程正是不同轨迹方程的具体体现.
1 用直译法求动点轨迹方程

A.圆 B.椭圆 C.抛物线 D.直线
解析设AB=2a(a>0),以AB中点为坐标原点,以线段AB所在直线为x轴,线段AB的中垂线为y轴建立平面直角坐标系,则A(-a,0),B(a,0).


结合题意可得(x+a)(x-a)+y2=1.
整理,得x2+y2=a2+1.

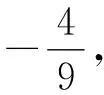


化简,得点M的轨迹方程为
2 用定义法求动点轨迹方程


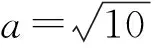
因为c=2,所以b2=a2-c2=6.


3 用相关点法求动点轨迹方程
例5在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,点D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹是什么?







即点P的轨迹方程为x2+y2=2.
4 用参数方程法求动点轨迹方程
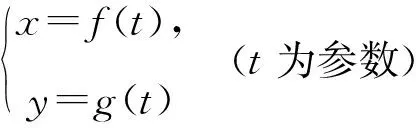
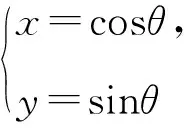
(1)求α的取值范围;
(2)求AB中点P的轨迹的参数方程.

(2)由已知,直线l的参数方程为
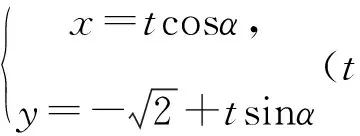
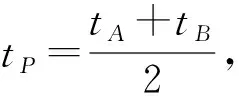


所以点P的轨迹的参数方程是


(1)将C的极坐标方程化为直角坐标方程;

解析(1)曲线C的直角坐标方程为
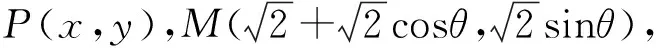



故P的轨迹C1的参数方程为
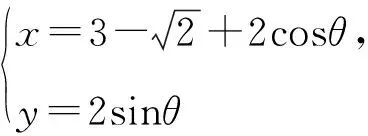


故曲线C与C1没有公共点.
5 在极坐标系中求动点轨迹方程


例10 在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρcosθ=4.M为曲线C1上的动点,点P在线段OM上,且满足|OM|·|OP|=16,求点P的轨迹C2的直角坐标方程.
解析设点P的极坐标为(ρ,θ)(ρ>0),点M的极坐标为(ρ1,θ)(ρ1>0),

因为|OM|·|OP|=16,
所以C2的极坐标方程为ρ=4cosθ(ρ>0).
所以C2的直角坐标方程为
(x-2)2+y2=4(x≠0).
以上就是五种关于求动点轨迹类型的梳理,只有理解了解题突破口,明确了最后答案的呈现形式,有计划、有准备地按照缜密的逻辑推理,问题自然迎刃而解[2].
教师在日常教学中,应注重培养学生学习知识的系统性、完整性.引导学生经历完整的研究过程,发现动点轨迹的本质,理解曲线的方程和方程的曲线之间的逻辑联系.在恰当的位置建立坐标系,将图形特点和规律反应到代数式中,实现曲线和方程的统一,这正是解析几何的魅力所在.同时,能够在具体情景中培养学生直观想象、数学抽象、逻辑推理、数学建模、数学运算等核心素养.

