利用数形结合思想 巧思妙解几何问题

罗志山

(海安市角斜镇老坝港初级中学,江苏 南通 226634)

初中数学课堂是学生掌握数学基础知识、训练基本技能、形成基本数学思想、积累数学活动经验的主阵地,也是培养学生高阶数学思维的主阵地[1].数形结合思想是一种重要的数学思想方法,是将抽象的数量关系与直观的图形结构结合起来进行思考的一种思想.在初中数学教学过程中,教师需培养学生数形结合意识,提高数形结合能力,从而提高学生运用所学知识分析问题和解决问题的能力.

1 利用数形结合思想妙解平行四边形问题

平行四边形是初中数学中一个重要的平面图形,它的性质在解题中有着广泛的应用.在与平行四边形有关的数学问题中,其主要涉及平行四边形的定义、性质和判定等知识,利用这些知识解决问题时,数形结合思想可以发挥重要作用.在初中数学教学中,教师可以借助数形结合思想,帮助学生理解平行四边形的概念、性质和判定,还可以帮助学生找到数学学习的灵活性和机动性.

在“平行四边形”教学中,教师可以给学生展示一些平行四边形的实际例子,比如铁路轨道、篮球场地等,通过观察这些实际对象的特点,学生可以直观地感受到平行四边形的形状和性质.然后,教师可引导学生观察并描述这些平行四边形的特点,如对边是否平行、对角是否相等等,从而帮助学生建立对平行四边形的初步认识.接着,教师可以为学生展示课堂例题,培养学生的应用能力.

例1如图1,在平行四边形ABCD中,设点E,F分别为边BC,AB上的一点,CF与AE相交于一点P,CF=AE.求证:∠APD=∠CPD.

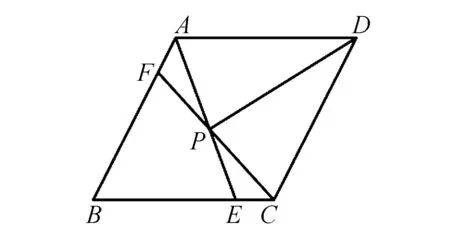
图1 例1题图

为使学生熟练运用平行四边形的性质解决本题,教师可帮助学生回顾平行四边形的性质.指导学生绘制平行四边形的几何图形,引导学生观察图形中的边、角、对角线,并与平行四边形的定义结合起来,探索平行四边形的性质.教师可要求学生测量平行四边形各边的长度和各角的大小,通过比较,学生发现平行四边形的对边相等、平行四边形的对角相等.同时,教师还可以引导学生观察平行四边形的对角线的特征,学生容易发现“平行四边形的对角线互相平分”.针对本题,在教师的指引下,学生积极思考,踊跃发言,得到了问题的证明方法.

证明如图2,过点D作DG⊥AE,DH⊥CF,垂足分别为G,H.连接DF,DE.

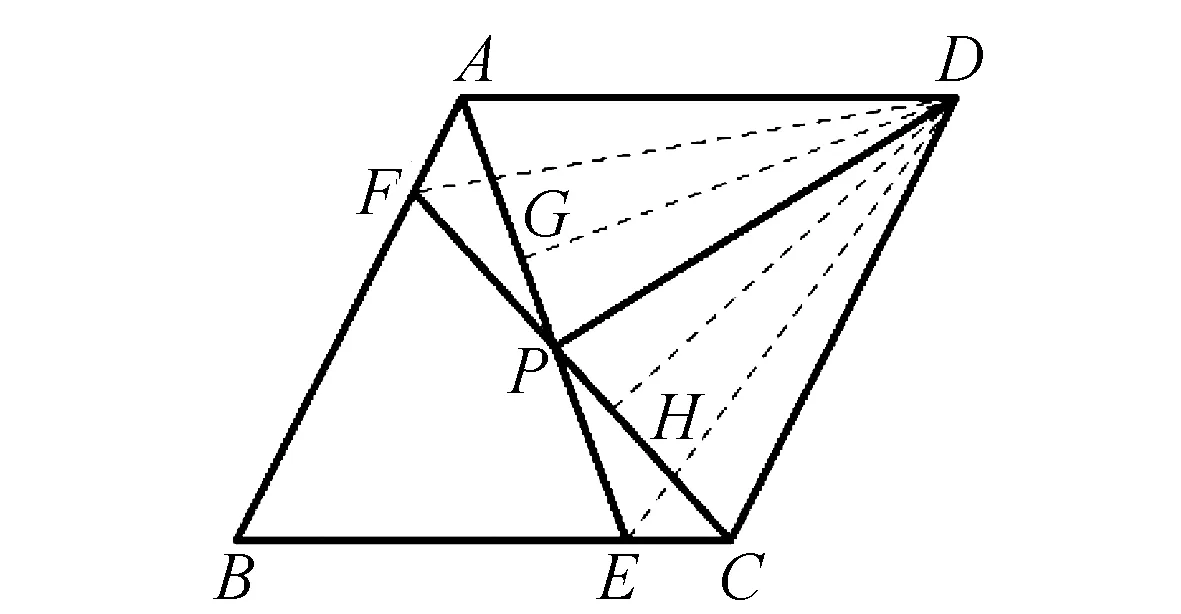
图2 例1题证明图

除此之外,教师还可以设计一些与实际生活相关的问题,要求学生利用平行四边形的性质进行推理和解答.例如,教师可以给学生一个房间的平面图,要求学生找出平行四边形.通过这样的问题设计,能够将数学知识与实际情境相结合,培养学生的逻辑推理能力和问题分析能力.

借助数形结合的数学思想方法,可为学生解决问题提供良好的数学解题思路,提高学生运用所学知识分析问题和解决问题的能力.在初中数学教学中,教师可借助数形结合的思想方法,激发学生学习数学的兴趣,提高学生的几何直观和几何推理能力.

2 利用数形结合思想妙解全等三角形问题

数形结合思想的应用非常广泛,不仅可以解决与平行四边形有关的几何问题,还可以解决与全等三角形有关的几何问题.教师可引导学生将数学概念与几何图形相结合,帮助学生更好地理解数学概念和几何图形的结构特征,从而提高学生运用所学知识分析问题和解决问题的能力.

在“全等三角形”教学中,教师可展示一些全等三角形,引导学生观察图形的特征,从而得到全等三角形的性质.首先,教师给学生展示两个全等三角形,并提醒学生注意图形中的对应边、对应角的大小关系.然后,教师让学生通过观察和比较,找出两个全等三角形中具有相等关系的边或角,从而发现全等三角形的对应边相等、全等三角形的对应角相等.接下来,教师可以设计一些有趣的几何问题,让学生利用数形结合思想解决.

例2 如图3,在△ABC中,点D在线段AC上,线段BD平分∠ABC,延长BA到点E处,使得BE=BC,连接DE,若∠ADE=38°,求∠ADB的度数.

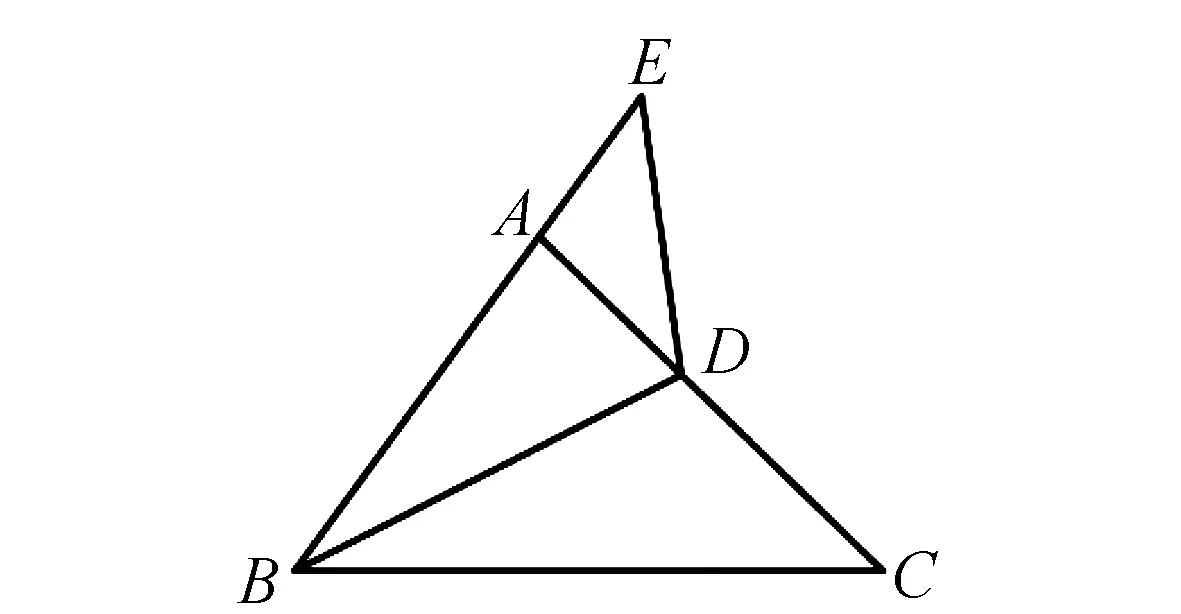
图3 例2题图

教师引导学生结合图形特征,对已知条件和所求角度之间的逻辑关系进行思考,利用数形结合思想求解.学生指出,从角平分线入手,根据全等三角形的性质可得出对应角相等,然后再借助假设法和等量代换得出最后的结果.教师对学生的求解思路给予充分肯定,并请学生写出求解过程.

解因为BD平分∠ABC,所以∠DBE=∠DBC.

在△BDE和△BDC中,

因为BC=BE,∠EBD=∠CBD,BD=BD,

所以△BDE≌△BDC,所以∠BDE=∠BDC.

设∠BDA=α,则∠CDB=∠EDB=α+38°,又因为∠CDA为平角,所以α+α+38°=180°,解得α=71°,即∠ADB=71°.

除此之外,教师还可以引导学生将数学概念与实际生活中的问题相结合,让学生意识到全等三角形在生活中的广泛应用.例如,教师可以给学生讲解全等三角形在建筑设计、地图绘制等领域的应用等.

借助数形结合思想方法,学生对几何知识有了更深入的理解,提高了学生观察和比较的能力.全等三角形的判定与性质是解决与全等三角形有关几何问题的工具,数形结合思想为学生提供了一种有效解决几何问题的方法,使学生灵活运用所学知识解决几何推理问题.因此,掌握全等三角形的概念可以帮助学生更好地理解和应用全等三角形的判定与性质解决实际问题,为学生未来的学习和发展打下坚实的基础[2].

3 利用数形结合思想妙用最值阿氏圆

阿波罗尼斯圆是一种特殊的圆,简称为阿氏圆,其特点是它的半径与焦点之间的距离成反比例关系,学生学习阿波罗尼斯圆的意义在于它代表了几何学中的一个重要概念,不仅具有理论上的价值,还有实际应用的意义.通过学习阿波罗尼斯圆,教师可以引导学生深入理解数学中的比例关系和图形的性质,帮助学生更好地理解和解决最值问题.

在“圆”的教学中,教师可以指出阿波罗尼斯圆的研究对于几何学发展的重要意义,扩展学生对圆形的认识,使学生能够更加全面地理解和应用圆的性质.通过研究阿波罗尼斯圆,教师可以引领学生进一步探索圆的曲率、切线和法线等方面的特性.在教学实践中,教师可以给学生呈现一个最值问题,求解一个三角形内切圆半径的最大值问题,然后引入阿氏圆的概念,并通过对几何图形的观察,让学生发现阿氏圆的半径与三角形的边长之间存在着某种关系.接着,教师可以引导学生运用数学知识,如勾股定理和三角形面积公式,结合阿氏圆的性质,推导出最值问题的解决方法.通过这样的教学方式,学生不仅能够理解数学规律,还能够培养学生的逻辑推理能力和分析问题的能力.

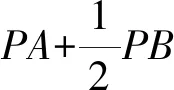
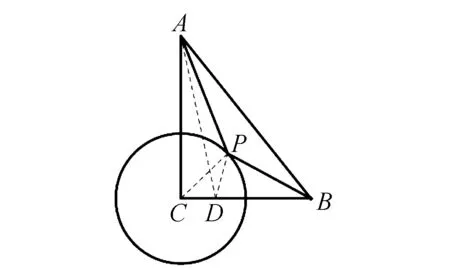
图4 例3题图

结合图形特征和已知条件,教师可以鼓励学生自主解答,培养学生的数学思维能力,提升学生的数学核心素养.其中一名学生提供了如下解题思路:

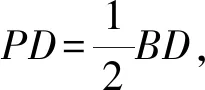
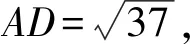
借助数形结合思想解决与阿氏圆有关的最值问题,为学生提供了锻炼几何推理思维的机会,帮助学生深刻理解数学最值问题的几何意义,从而为学生的数学学习提供更加丰富和深入的活动体验[3].

总之,数形结合思想是一种非常重要的数学思想方法,在初中数学解题中有着广泛的应用.几何问题不仅可以培养学生的空间想象力和几何推理能力,而且可以培养学生的几何直观.因此,在初中数学教学中,教师也可以将数学概念与几何图形相结合,让学生能够更直观地理解和应用数学知识.数形结合思想是一种有效解决几何问题的思想方法,可以提高学生运用所学知识分析问题和解决问题的能力,提升学生的数学核心素养,促进学生全面发展.