西藏县域初中数学教学促进学生思维参与的教法探析

李江专 西藏昌都市察雅县中学

公平、有质量的教育是我国新时代教育的显著特征，大力推进城乡教育优质均衡发展契合人民群众对优质教育的期待。党的十八大以来，西藏教育深化改革，加快推进教育现代化，全区教育与全国同步进入高质量发展新阶段。［1］西藏县域中小学学生人数在全区基础教育学生总数中占比大，关乎全区教育高质量发展进程。当前，西藏县域中小学数学教学整体质量偏低［2］，主要是弱化了数学课堂学生学习的主体地位，忽略了学生数学学习思维参与的重要性。《义务教育数学课程标准（2022 年版）》（以下简称“课程标准（2022年版）”）要求，教学要善于引导学生思维参与和数学思考。结合我区县域初中生数学学习实际，亟需将数学课堂转向以注重学生思维参与为中心的教学。文章在阐述学生数学学习思维参与的重要性、西藏县域初中数学课堂学生思维参与现状的基础上，探究数学课堂教学促进学生思维参与的教学方法，对提高我区县域初中数学教学质量具有现实意义。

一、中小学数学课堂学生思维参与的重要性

（一）学生思维参与是数学课堂教学质量的关键因素

“课程标准（2022年版）”指明，中小学数学教学要加强学生对数学概念的理解，数学学习过程是学生不断思考和探索的过程。学生理解数学概念、思考数学问题，必然需要学生的思维参与。学生思维参与是学生数学学习的关键性学习行为。中小学数学课堂需要学生观察、思考和联想，若缺少学生的思维参与，也就难以达到数学知识学习内化的目的，数学课堂的教学效果势必大打折扣。顾明远、史宁中、张晓斌等教育专家认为，数学课堂的教学效果关键看学生数学思维在课堂投入、交流及碰撞的情况。从数学学科特点来分析，数学具有较强的抽象性、逻辑性等鲜明特征，需要学习者进行数学思考、逻辑推理、合理论证、质疑等，学生思维元素的参与就显得至关重要。

（二）学生思维参与度与数学课堂教学质量呈正向关系

中小学数学课堂学生思维参与程度与数学课堂教学效果有直接关联。在一定程度上，学生思维品质、思维参与程度，决定了数学课堂学生的学习质量。［3］有研究表明，数学课堂学生思维参与程度与教学质量呈现出显著正相关，表明学生对数学课堂学习内容的思考越深入，课堂教学效果就更加凸显。在学生思维参与下的数学课堂，学生思维参与程度越高，更容易理解、弄通教学内容的难点部分；从而突破数学课堂教学难点，实现有质量的数学课堂教学，这是逻辑之中的事情。教师引导学生深度思考，既释放学生学习潜能、主动建构知识体系，又能体现学生课堂学习主体地位，使数学课堂焕发出强大生命力。

二、西藏县域初中数学课堂关注学生思维参与的现状

（一）教师对数学课堂学生思维参与的重要性认识不足

笔者作为西藏县域中小学数学教育研究者，发现当前西藏县域初中数学教师在教学方面主要面临学生数学基础弱、教学任务重等多重压力。调研发现，西藏县域初中生缺乏数学学习主动性，数学课堂教师宁愿相信自己讲、不愿相信学生主动探究学。在教学方式上，数学教师习惯采用灌输式、解题训练的方式教学。［4］数学教师提问时，采用“是不是”“对不对”简单的集体式提问居多。“你讲我听”“你说我记”传授式课堂教学、教师“自问自答”代替了学生数学思考和探索的学习过程，阻碍了学生数学学习的思维参与，抑制了学生思维参与的积极性，背离了学生学好数学需要理解、思考这一规律性认识。由于学生对数学课堂教学内容的学习参与、思考和理解不够，缺少对新知识学习的生长点，课堂往往失去了学生自主内化数学新知识的生命力。

（二）教研关注数学课堂学生思维参与的力度不够

从学校指导数学教研工作的层面来分析，我区县域初中开设的每门课程有不同的学科特点，分管学校教学校级领导、教务及教研人员来自不同的学科门类，术业有专攻，不易从学科专业的视角关注数学课堂学生思维参与方面的情况，往往从教研组教研活动开展频次、教师批改作业情况、教学进度等方面进行检查，缺少以学生思维参与的视角来指导数学教学工作。从学校数学组开展的教研活动来看，调研发现，我区县域初中数学教研活动内容局限于听课、评课、培优、后进生转化、教学方法讨论等常规性教研，涉及数学教学促进学生思维参与为中心的专题数学教研活动不多，探索数学课堂教学促进学生思维参与的教研工作还不足，尚需加大探究数学教学怎样促使学生思维参与的教研力度。

三、西藏县域数学课堂促进学生思维参与的教学方法

（一）注重数学课堂教学提问，引发学生的思维产生

一方面，借助教学情境中的问题来引发学生思维的产生。数学课堂教学需要设计真实的教学情境，问题在情境中产生，教学情境是为学生思考情境中的问题而作的铺垫，用情境中的问题激发学生思维的产生。因此，数学教师设计的课堂教学情境应当是学生熟悉的，以能够激发学生积极学习为宜，学生阅读情境后对其中的问题产生兴趣，以此激发学生对问题的探究欲，对情境中的问题进行主动思考，并探索解决的办法，学生的思维也就自然生成。当然，设计教学情境中的问题应与本堂课的教学目标直接关联，学生在思考、探索、解决问题的过程也是学习目标达成的过程。

另一方面，通过课堂教学追问来驱动学生思维的产生。数学课堂重视学生思维参与是授课教师关注学生学习行为的教学体现。数学课堂教师结合教学需要，因势利导使用教学问题串，凭借课堂教学追问激奋学生思维的持续运转。为使学生的思维前后链接，问题串应当有梯度、循序渐进。教师对课堂追问需要预先考虑的是，学生对问题的解决需要建立在学生已有的基础知识及经验之上，追问的难度要符合学生学习最近发展区，旨在达到课堂提问促进学生思维持续运转的效果。

（二）借助直观图形，发展学生的形象思维

初中数学课堂教学借助图形的直观性，能帮助学生形象地理解图形之间的关系。基于此，数学课堂教师引导学生从图形的直观感知到概括出学习内容的本质，学生经历直观感知到掌握学习内容本质的学习过程来培养学生的形象思维。例如，八年级上册人教版“三角形的边”的教学，如甲、乙、丙三地恰好在ΔABC的三个顶点，如图1 所示。从A 点（甲地）出发沿三角形的边到B 点（乙地）有几条线路？哪条线路最近？对照图1 引导学生直观感知，将ΔABC的A、B两个顶点看成定点，由数学基本事实：两点之间线段最短，即AC+BC＞AB ①；同样，将ΔABC的A、C 看成定点时,得到AB+BC＞AC ②；将ΔABC的B、C 看成定点时,得到AB+AC＞BC ③。由①②③式得出结论：三角形任意两边之和大于第三边，也就是判断三条线段能否围成三角形的充要条件。

图1 任意三角形ABC

思维启发1：教学追问，继续催生学生思考。上述判断三条线段能否组成三角形的①②③三个条件，能否进一步简化？教师引导学生数学思考，三条线段的长度分别对应三个正数，引导学生从三个正数的逻辑大小关系上感悟出：三条线段只要达到较小的两条线段之和大于最长线段的条件，也就必然满足三角形任意两边之和大于第三边的条件。促成学生在思维上发现蕴含其中数的逻辑大小关系。

思维启发2：要求学生继续思考，将①②③分别变形得到AC＞AB-BC、BC＞AC-AB、AB＞BC-AC，由此得到“三角形任意两边之差小于第三边”，该结论正是“三角形任意两边的和大于第三边”推导出的结果。

得出结论：判断三条线段组成三角形的条件，在方法上归为只需要判断“较小两条线段的和是否大于最长线段”。该学习成果正是学生思维参与得到的收获，这样将三角形“边”的学习内容理解得更透彻、掌握得更明白。

（三）重视数学公式推导过程教学，锤炼学生思维品质

西藏县域初中数学课堂重视数学公式推导过程的教学，学生既可厘清数学公式的来龙去脉，又可在探索、推导数学公式的过程中锻炼他们的思维品质。例如，人教版八年级上册“多边形的内角和”的教学，本课教学目标是探索并掌握n(n≥3)边形的内角和公式。

以学生已掌握的“三角形内角和180°”为经验基础，求任意一个n边形内角和这个未知的问题，引导学生在认识上形成用已知推未知的思维。也就是，需先将多边形内角和的问题转化为一个多边形能分成多少个三角形的问题。

设计教学片段，启发学生学习思维。师：怎样将任意一个多边形划分为三角形？生：连接多边形的对角线。教师及时评价学生的思考结果，“很好”；教师顺势追问：“从多边形的一个顶点出发，可以作出多少条对角线，这些对角线将该多边形分为多少个三角形？”要求学生分组合作探究出：从n边形的一个顶点出发，与其余各顶点相连，能分成（n-2）个三角形，n边形的内角和就等于（n-2）个三角形的内角和。

学生在探索“任意一个多边形能划分为多少个三角形”的过程中有困难时，教师不妨引导学生画出具体的三角形、四边形、五边形……来助力他们探索出规律，同时建立表1帮助学生经历思维的过程。

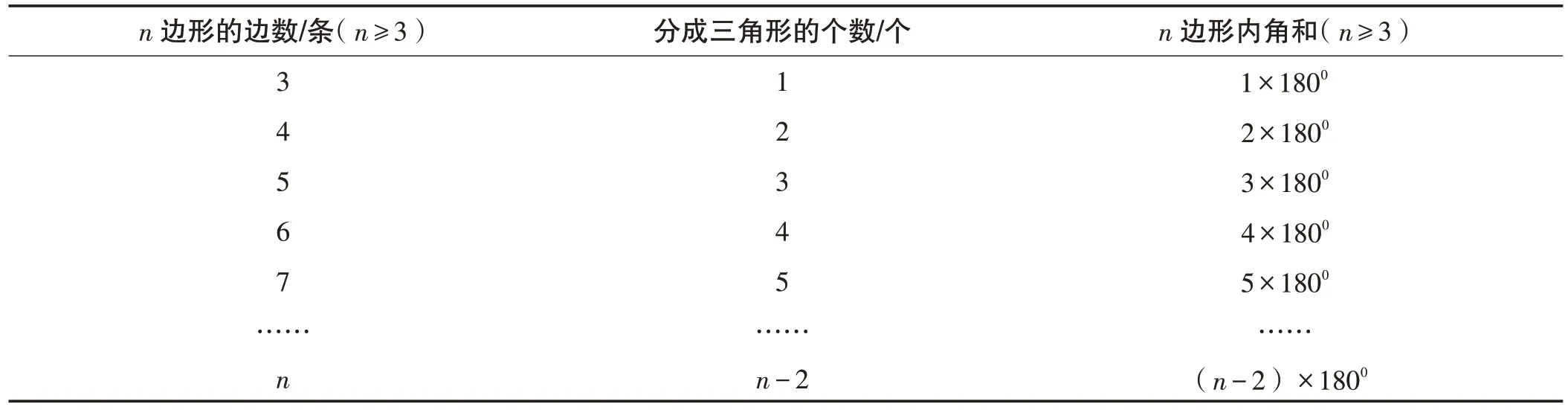
表1 多边形的边数与多边形内角和的对应关系

教师启发学生继续思考，求任意一个多边形内角和的问题，除了连接多边形的对角线方法外，还有另外新的分法吗？激励学生探索出新的分法：在多边形内任取一点，将此点与多边形各顶点相连接。引导学生观察发现，按照此分法多边形的每一条边就对应一个三角形，n（n≥3）条边的多边形就被分成n个三角形，多边形的内角和就等于n个三角形内角和减去一个周角，即1800n-3600，再进行整理，同样能推导出多边形内角和公式：（n-2）×1800。

重视学生思维参与的数学课堂教学是落实以学生为学习主体教学理念的重要途径。重视数学公式推导过程的教学是发展学生思维的有效教学方式。为促进学生数学思考，在实践教学中需要教师以包容、激励的教学姿态，并做到善于启发式教学。当学生感到数学公式推导困难时，需要教师为学生搭建学习的脚手架，助力学生继续思考。长期坚持，学生的数学思维将不断得到提升。