基于离散元法的大豆螺旋喂料装置流量公式修正
◎ 王震民,徐天明,赵瑞营,李召峰,夏朝勇
(郑州中粮科研设计院有限公司,河南 郑州 450001)
螺旋输送装置结构简单、维修方便、密封性能较好,且成本较低,在粮食、医药及化工等诸多领域都得到了广泛应用[1]。随着现代工业的快速发展,螺旋输送机在粮食领域内的应用愈发广泛,针对螺旋输送装置的各项关键参数进行优化设计也成为各界学者日益关注的重点[2]。梅潇等[3]在单质点法的基础上,以细沙为研究对象,利用MATLAB 函数拟合功能,对螺旋输送生产率模型进行修正,较为准确地预测了螺旋输送装置的生产率。林苑等[4]在离散元法的基础上,以小米为研究对象,对螺旋输送装置的流量公式进行修正,得到了小米物料的流量理论计算公式,验证了小米物料流量理论计算公式的合理性。徐雪萌等[5]基于正交试验,以小麦粉为研究对象,建立了影响因素与响应值之间的二阶回归方程,对螺旋喂料装置的流量计算公式进行修正,为小麦粉螺旋输送装置的参数优化提供参考。
由于螺旋喂料装置内部物料流动性较为复杂,对内部物料各项参数进行直接检测存在很大的难度,离散元法的出现为解决这一难题提供了方法和途径,因此在对散粒体物料进行分析时,大多学者选用离散元法对问题进行简化求解。赵春等[6]采用离散元法对土壤肥料混合过程中的螺旋混合轴进行结构设计,在EDEM 中对颗粒运动轨迹进行仿真分析,得到了较好的结构参数。薛忠等[7]基于离散元法对螺旋式排肥器进行性能模拟试验,提高了螺旋式排肥器对颗粒肥料的排肥稳定性和均匀性,得到了最佳参数组合。辛垚谕等[8]针对螺旋输送机内部受力问题,基于离散单元法和Hertz 接触理论建立物料-物料、物料-装置之间的接触模型,对颗粒的输送特性进行分析,为后续优化设计奠定基础。为解决大豆螺旋输送实际流量与理论流量计算公式存在较大误差的问题,本文选用Box-Behnken 试验对大豆螺旋输送流量公式进行修正。通过Inventor 三维建模软件建立螺旋输送模型,导入EDEM 中进行仿真分析,以螺距、内径和螺旋转速为影响因子,结合仿真结果在Design Expert 中进行优化分析,得到流量计算的修正公式,以期为大豆螺旋喂料装置的设计提供参考。
1 理论基础
1.1 物料运动状态分析
物料在螺旋喂料过程中,受到螺旋叶片对其施加的作用力而发生相对运动,选取输送物料中的某一单颗粒作为研究对象,分析粉体在喂料过程中的运动状态。将螺旋叶片展开,选取距离螺旋中心轴线距离为h的颗粒物料进行分析,假定为颗粒P。颗粒在螺旋叶片以及其他颗粒对其施加的外力作用下,在喂料装置内部发生相对运动,其速度分解图如图1 所示。
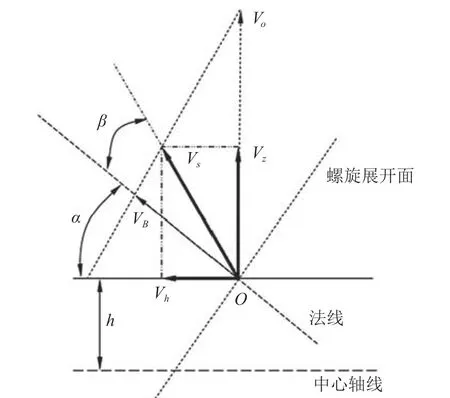
图1 大豆颗粒运动分析图
由图1 可知:
式中:S为螺距,mm;n为转速,r·min-1,Vs为颗粒速度,m·s-1;Vo为轴向速度,m·s-1;d为螺旋内径,mm,Vh、Vz为Vs沿坐标轴的两分量,m·s-1。
1.2 流量计算公式
传统螺旋输送过程中流量按公式(7)计算[9]。
式中:Q为螺旋喂料量,t·h-1;D为螺旋叶片直径,mm;φ为粉体物料填充系数;n为螺旋轴转速,r·min-1;ρ为粉体物料密度,kg·m-3;S为螺距,mm;C为倾斜修正系数;K为螺旋叶片影响系数。
1.3 离散元颗粒运动方程
在离散元法中,可以通过力-位移关系对颗粒进行受力分析,颗粒的位移可以由牛顿第二定律进行求解,如下所示。
式中:v为颗粒i的速度;Fij为壁面或颗粒i对颗粒j的力,Fij=Fijn+Fijt;mig为颗粒i受到的重力;ωi为颗粒i的角速度;Tij为壁面或颗粒j施加在颗粒i上的力矩;Ii为颗粒i的转动惯量。
颗粒间的相互作用如图2 所示。
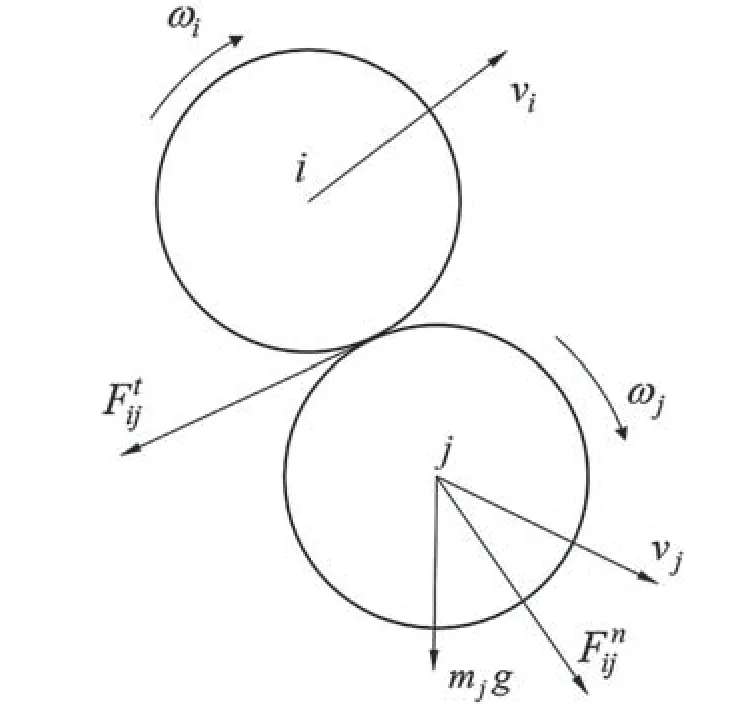
图2 颗粒间相互作用图
2 Box-Behnken 试验及流量公式修正
根据实际情况需求,以大豆物料为研究对象,采用EDEM 离散元仿真软件与Design Expert 优化分析软件相结合的方式,进行Box-Behnken 试验。以转速、螺距和内径为影响因子,以螺旋喂料装置的流量(Q)为响应值,以仿真所测得流量值与流量公式计算所得流量值的比值为对比参考,对大豆螺旋喂料装置的流量公式进行修正。
2.1 大豆离散元仿真参数
用离散元仿真软件对大豆螺旋喂料进行仿真,仿真参数的准确性直接决定了仿真结果,因此参数的选取十分重要,根据相关参考文献[10-14],大豆离散元仿真参数如表1 所示。

表1 离散元仿真参数表
2.2 试验因素
结合实际情况,螺旋喂料装置转速选择在80 ~120 r·min-1,螺距选择为60 ~80 mm,内径为80 ~100 mm。由此选定Box-Behnken 试验的各自变量的因素水平,如表2 所示。

表2 响应面因素水平表
2.3 试验设计及结果分析
Box-Behnken 试验结果见表3。应用Design-Expert 对Box-Behnken Design 结果进行多元回归拟合,得到拟合回归方程为
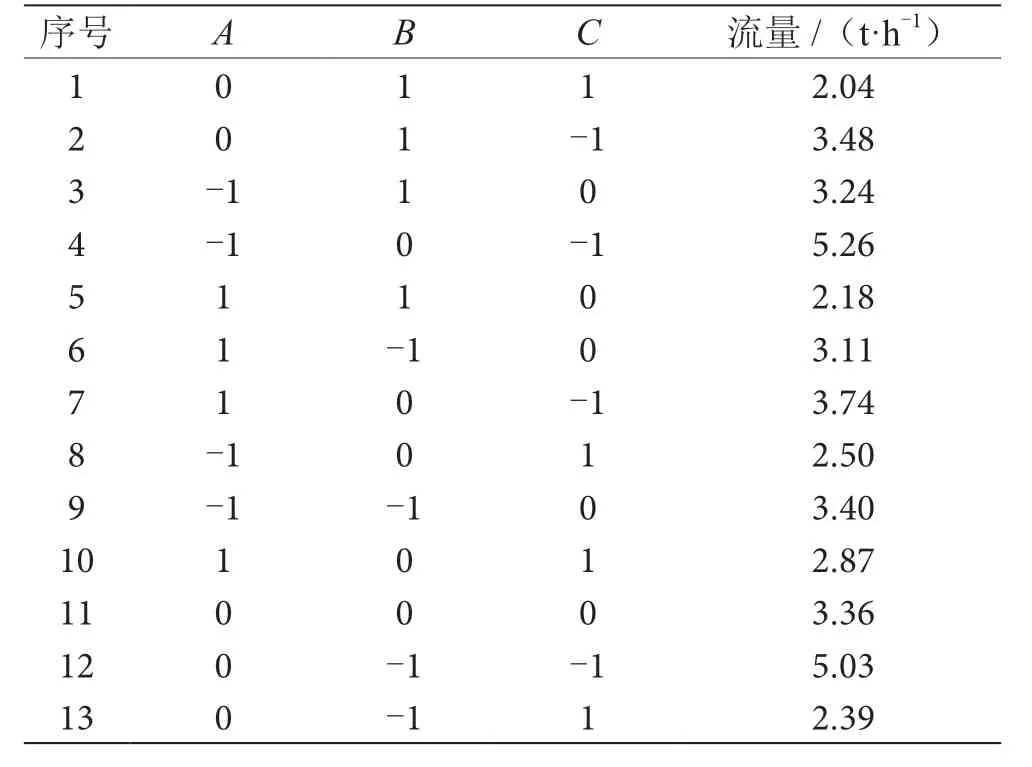
表3 Box-Behnken 试验结果表
对Box-Behnken Design 方案方差分析如表4 所示。由表4 可知,回归模型显著(P<0.01);转速(A)、螺距(B)、内径(C)、转速-螺距(A-B)、转速-内径(A-C)、螺距的二次项(B2)的P值均<0.05,表明上述各项参数对休止角响应值的影响较为显著,验证了模型的合理有效性。试验中变异系数CV=5.9%,表明设计试验的可靠性较好。决定系数R2=0.99,校正决定系数R2adj=0.96,预测决定系数R2pre=0.905,均>0.9,说明模型与实际情况具有较高的吻合度。试验精密度Adep Precision=19.08,说明模型的精确度较高。
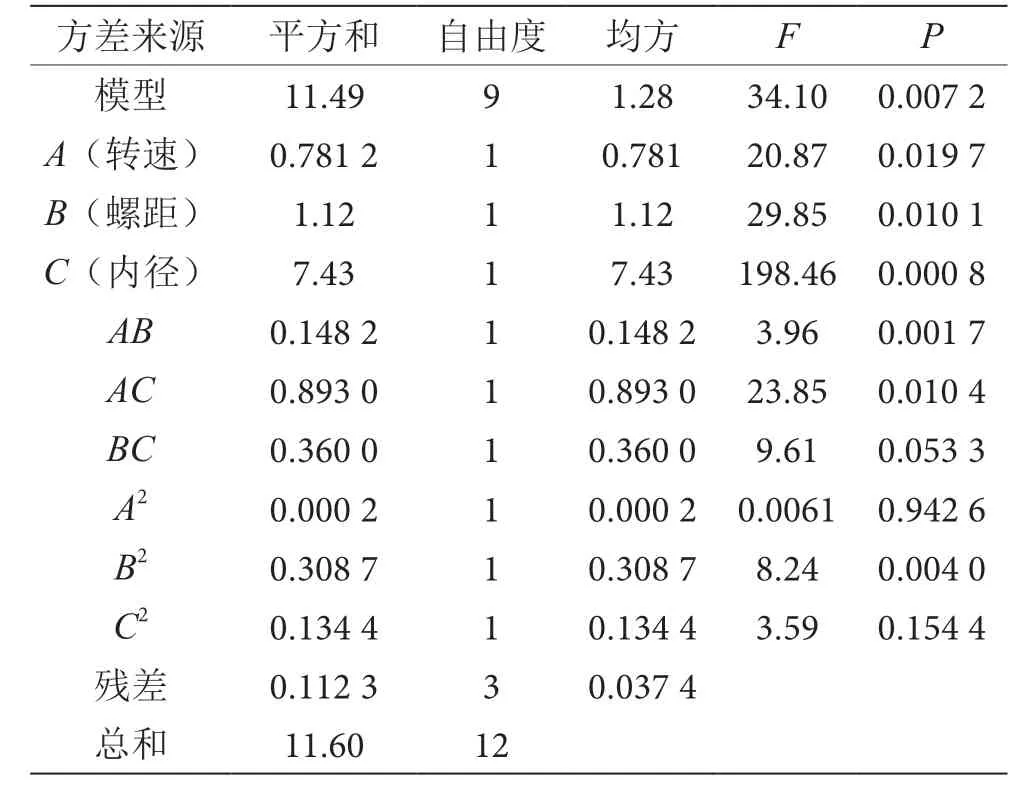
表4 Box-Behnken Design 二次回归模型方差分析表
根据表4 结果,在不影响模型精确性的前提下,排除对响应值影响较小的因素(BC,A2,C2),对模型进行优化,优化后方差分析如表5 所示。失拟项P=0.001 6,变异系数CV=6.74%,决定系数R2=0.95,校正决定系数R2adj=0.89,预测决定系数R2pre=0.81,试验精密度Adep Precision=24.06。从以上数据结果可知,模型在拟合性、准确度以及可靠性方面均有所提高,相对优化前有所改善,优化后回归方程为
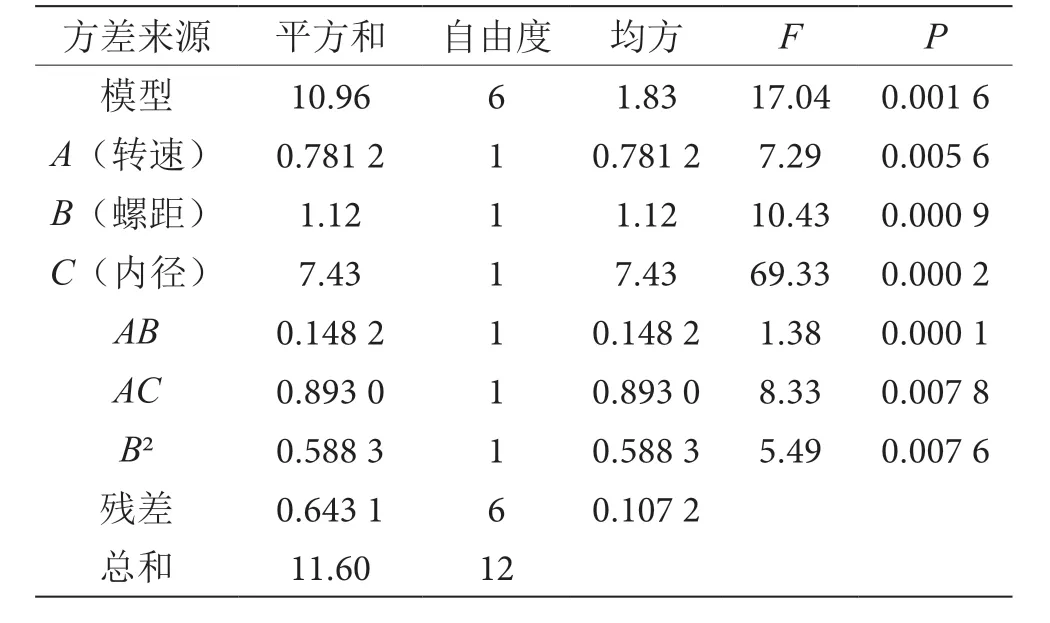
表5 Box-Behnken Design 优化回归模型方差分析表
通过优化后的回归方程可知,修正后大豆螺旋喂料装置的流量公式为
式中:Qx为修正后流量,t·h-1。
2.4 回归模型交互效应分析
对回归模型优化后的方差分析结果可知,转速-螺距(A-B)和转速-内径(A-C)的P<0.01,对流量响应值的影响极为显著,在Design-Expert 软件中绘制出转速-螺距(A-B)和转速-内径(A-C)交互作用下的三维响应曲面,可得到各交互项对响应值的影响程度,如图3 所示。由AB响应曲面可知,相对于转速(B)的响应曲线而言,螺距(A)的响应面曲线更陡,表明其对质量流量响应值的影响更为显著。由AC响应曲面可知,相对于内径(C),螺距(A)的响应面曲线更陡,表明其对质量流量响应值的影响更为显著。
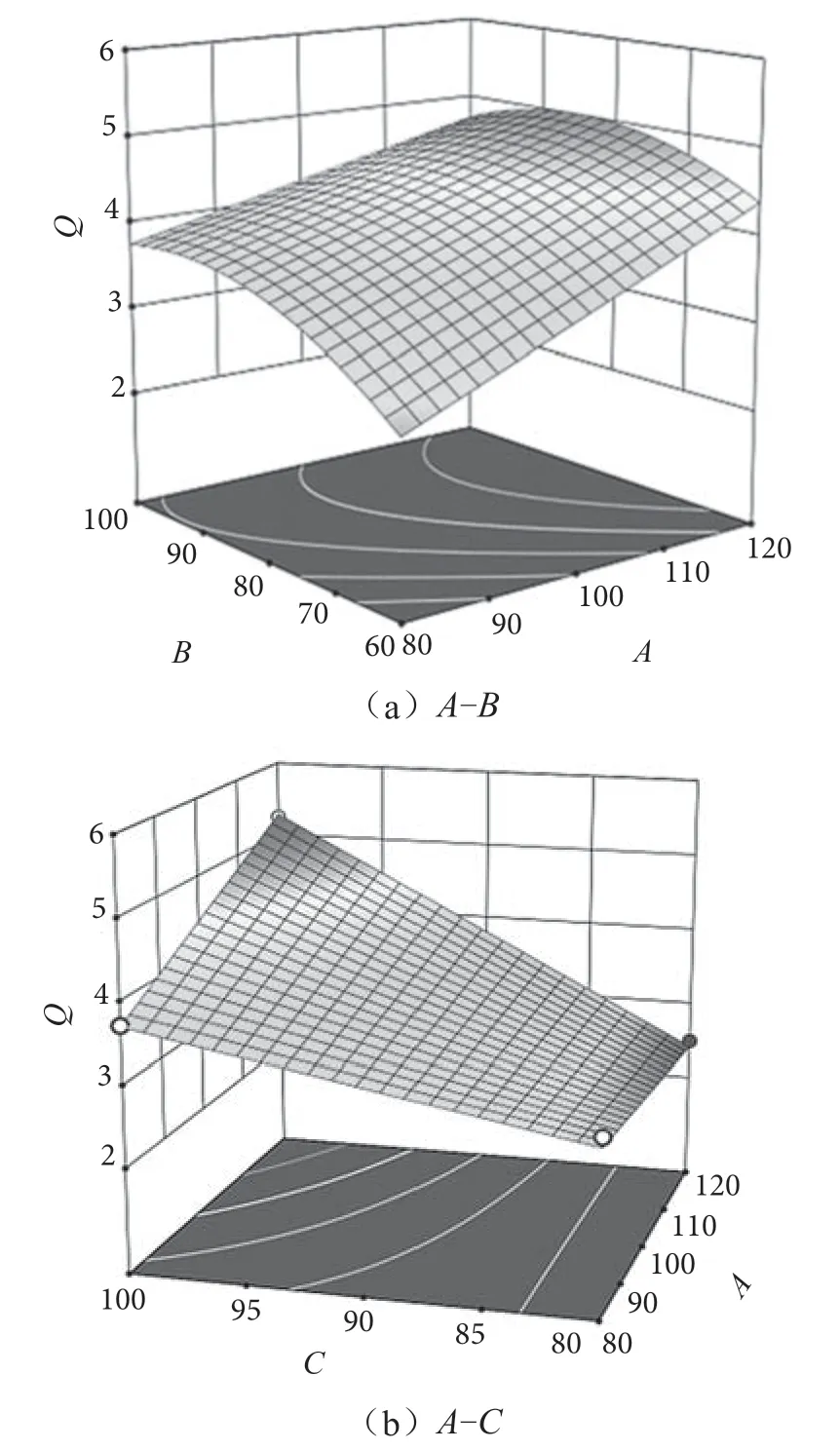
图3 AB 与AC 交互响应图
3 仿真试验验证
3.1 设计要求
螺旋输送物料为大豆,物料综合特性系数A=65,填充率φ=0.47,物料容重r=0.7 t·m-3,转速n=100 r·min-1,管径D=100 mm,螺距S=80 mm,根据设计要求D、S、n的取值以及修正后流量公式可得到,大豆螺旋喂料的流量理论计算值为1.908 t·h-1。
3.2 仿真过程及结果分析
根据设计要求,在Inventor 三维建模软件中,按照各参数建立大豆螺旋输送装置的仿真模型,为尽可能提高计算效率,对模型进行简化处理后导入EDEM中,如图4(a)所示。结合相关参考文献[15-18],对大豆物料选用球形颗粒,仿真过程如图4(b)所示。
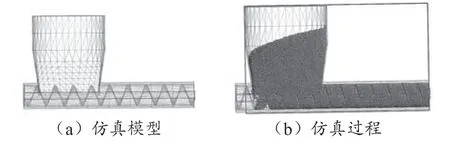
图4 仿真分析图
仿真结束后,在后处理模块选择流量传感器对物料流量进行实时检测,将数据导入Origin 中进行处理绘图,取输送过程中的两个时间段进行分析,如图5 所示。由仿真结果可知,物料的输送流量平均值为0.559 kg·s-1,与修正后流量公式计算值0.305 kg·s-1误差为5.22%,在误差可接受范围内,表明了修正公式的准确性。
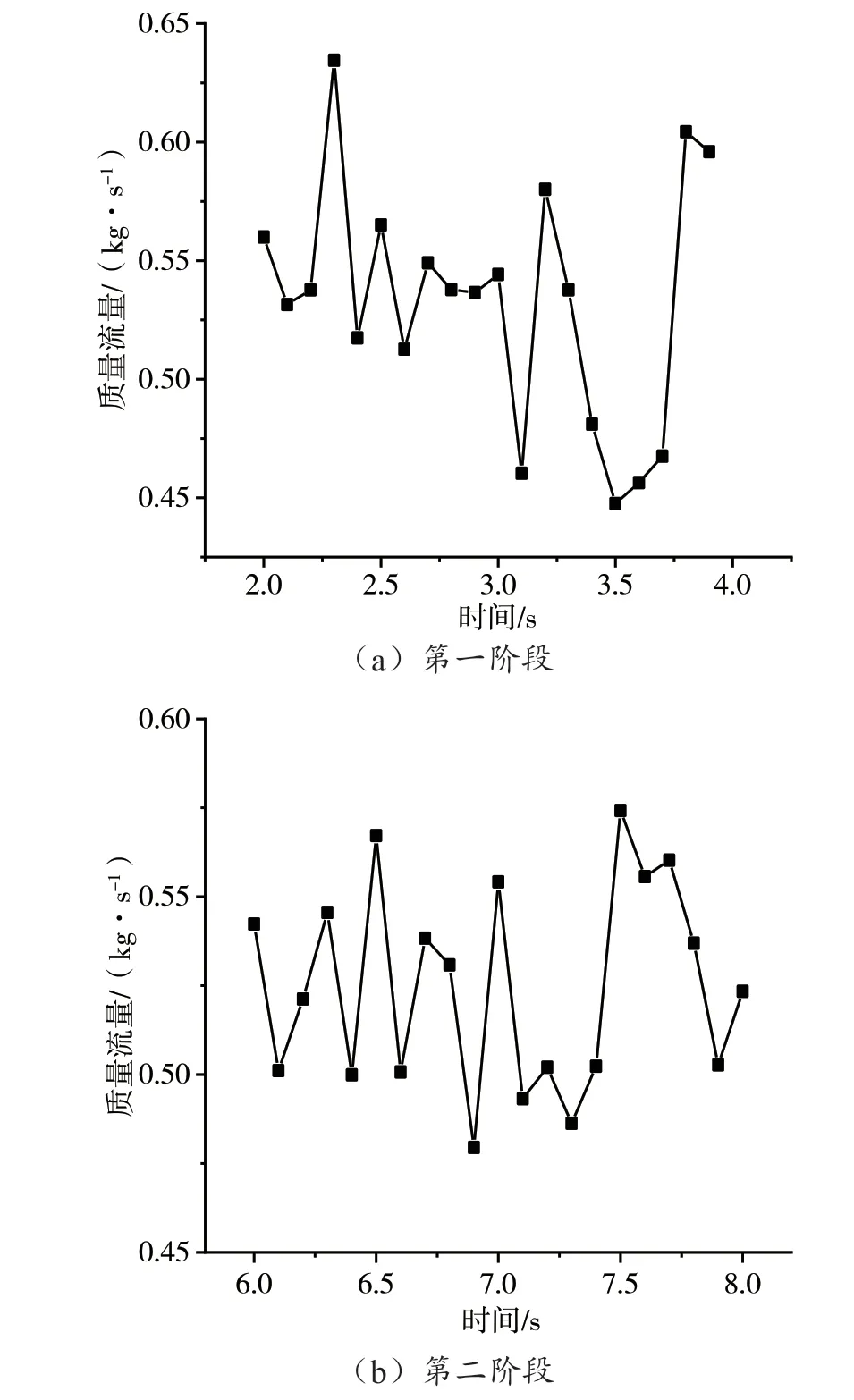
图5 实例仿真质量流量图
4 结论
针对大豆物料螺旋喂料装置由传统计算公式所得流量值与实际流量误差较大的问题,采用响应面法对传统流量计算公式进行修正,在Design Expert 中,以流量为响应值,以对流量影响较为显著的螺距、内轴径和转速为影响因素设计Box-Behnken 试验,影响因素与响应值之间的二阶回归方程,求得流量值的修正公式。为验证修正公式的准确性,根据相关参数在Inventor 中建立大豆螺旋喂料装置的简化模型,导入EDEM 中进行离散元仿真,有仿真结果可得流量值为2.013 t·h-1,将相关参数代入修正后流量计算公式可得计算值为1.908 t·h-1,两者误差为5.22%,在误差可接受范围内,表明修正公式的合理准确性,为大豆螺旋喂料装置的流量计算提供参考。此外,文章通过仿真进行流量公式修正,虽然参考相关文献确定仿真参数,在一定程度上能够降低仿真误差对修正结果的影响,但不同物料各项参数有所差异,后续可针对大豆的仿真参数进行进一步修正,进一步提高仿真的准确性,为螺旋喂料仿真提供更准确的参数。

