衬层材料参数对水润滑夹心轴承静态性能的影响*

解忠良 杨 康 田佳彬 张雪冰 焦 见

(1.西北工业大学工程力学系 陕西西安 710072；2.西安电子科技大学机电工程学院 陕西西安 710071；3.武汉第二船舶设计研究所 湖北武汉 430064)

轴承作为旋转机械的支撑部件，既承担了转轴的重力和负载，又影响着整个传动系统的动态特性，其中滑动轴承又因具备工作平稳、可靠、润滑性能良好等优异性能，被广泛应用在船舶、机床、电机、仪表、冶金等设备[1]。传统的滑动轴承以油为润滑介质、金属为轴瓦材料，这样的状况造成了大量油料和稀有金属的浪费。此外，油润滑的轴承在工作中会产生大量的热[2]，这种状况会直接影响到轴系的工作效率。船舶上使用的轴承更是会发生漏油的风险，从而对海洋生态环境产生恶性影响[3]。因此，西方国家早已出台了一系列禁止以油为润滑介质的船舶在内陆河航行的政策[4]。

鉴于油润滑技术存在的诸多缺陷，工程中一直在寻找可以有效避免这些缺陷的方法，于是在20世纪30年代便提出了以水做润滑介质的理念。水作为来源最广泛的资源，代替油作为滑动轴承的润滑介质，具有节能、高效、清洁、安全、可靠、无污染、比热容大等优点。此后，在国内外学者近一个世纪的研究探索下，水润滑轴承技术已经取得了重大进展。目前水润滑轴承被广泛应用于众多领域，包括高技术船舶推进系统[5]、海洋平台定位系统、海上作业的油井、船用水泵、螺旋桨、水电泵站、电厂[6]等场合。但是，与油相比，水作为润滑剂有着明显的弊端，水的黏度较低，使得轴承动压水膜难以形成，且形成的水膜厚度较小、承载能力较差[7]、极端工况下润滑不到位，从而直接影响轴承的使用寿命。而水润滑轴承的材料一般为弹性模量较小的非金属材料，在外载荷的作用下轴承又难免发生弹性变形，对水润滑轴承的润滑特性产生负面影响。

近年来，针对如何提高水润滑轴承润滑性能的研究备受国内外学者关注。目前对于水润滑轴承性能的改善主要从改善结构或选择材料两方面出发。改善结构方面，在轴瓦上开沟槽以及添加表面微织构研究方法倍受学者们的青睐；选材方面，主要以承载力大、摩擦因数低为标准。

目前，在水润滑轴承结构设计方面，产生了许多成熟的研究成果。WODTKE和LITWIN[8]开展了轴向槽水润滑艉轴承工作时热现象问题的研究，分析了影响水润滑轴承热效应现象产生的原因，解释了受限轴向流促进的凹槽回流决定了轴承温升这一现象，探明了整体系统温度变化的决定性因素。王娟等人[9]开展了表面织构对水润滑轴承承载性能影响的研究，建立了有织构和无织构水润滑聚合物轴承模型，分析了不同转速、内衬材料、弹性模量对织构轴承水膜压力及承载力的影响规律。XIE等[10]开展了探究微腔水润滑轴承的微观界面润滑性能的研究，探讨了操作条件和结构参数对流体特征的影响，揭示了微腔中的流线、压力、涡流黏度的变化，分析了微腔的润滑机制以及润滑性能随着结构参数变化的规律，获得了轴瓦上的腔体在微观上形成额外动压从而在宏观层面提高润滑性能的结果，实验结果可为优化轴承表面形貌设计提供理论依据。在此基础上，XIE等[11]还开展了轴向不对称槽水润滑轴承的流固耦合动态性能的研究，探讨了沟槽类型、偏心比、旋转速度、沟槽位置处于上升区/下降区对动态行为的影响，获得了轴向不对称槽的存在放大增强了微观结构中水动力效应的结果，实验成果为优化轴承表面微观结构设计提供一定理论依据。另外，关于水润滑轴承轴瓦材料的研究也产生了诸多成果。王玉君等[12]构建了双向流固耦合水润滑模型，对4种不同材料的织构型轴承进行优化设计，研究了4种材料在不同工况下的承载力和摩擦力，探明了弹性模量与水润滑轴承静态性能的关系。GUO等[13]开展了新型仿生材料水润滑艉轴承摩擦学特性的研究，经过实验对比分析选出了具有良好润滑性能的水润滑艉轴承仿生材料。WANG等[14]开展了水润滑轴承的摩擦磨损性能研究，分析了复合材料的力学性能和摩擦学性能，揭示了复合材料的润滑机制。杜媛英、李明[15]建立了水润滑双向流固耦合模型，研究了赛龙、飞龙、丁腈橡胶和超高分子量聚乙烯4种新型材料在偏心率为0.6时的水润滑衬层变形及水膜压力分布情况。WU等[16]以聚乙烯蜡(PEW)作为水润滑轴承主要材料，开展了其对聚氨酯基复合材料耐磨性影响的研究，探究了不同载荷条件下复合材料的磨损行为，评价了复合材料的耐磨性，结果显示了PEW材料有助于水润滑轴承形成具有良好润滑性能的润滑膜。此外，LIANG等[17]开展了海浪冲击对水润滑轴承瞬态启动性能的影响研究，研究了海浪冲击的振幅、方向和进入时间对轴承启动性能的影响，结果表明轴承在初始启动阶段具有较强的瞬时振动，而适当的冲击载荷可以抑制甚至消除这种振动现象，该实验结论可为船舶推进系统的平稳启动提供参考。XIE等[18]开展了流固耦合对水润滑轴承润滑性能影响的研究，比较了在同一工况下7组不同润滑模型的润滑性能的区别，探讨了偏心比、衬套的厚度对周向压力分布的影响，得到了不同的偏心比、润滑模型分别具有不同水膜压力分布的结果。李文锋等[19]建立了水润滑轴承的弹流润滑模型，分析了水润滑橡胶层厚度对轴承弹流润滑性能的影响。FENG等[20]提出了一种考虑湍流、热力学、不对中效应的水润滑模型，揭示了负载能力、摩擦功耗损失、流量等因素与转速、偏心比的关系，阐明了湍流、热力学与水润滑轴承润滑性能之间的机制。

综上所述，在结构方面水润滑轴承的研究已经取得了很大的进展，但在轴瓦材料方面研究内容大都是利用数值解法或实验对某几种特定材料进行研究分析，进而比较出特定工况下几种材料的性能，根据需求选择合适的材料应用于实际，而对于在某一范围内材料属性变化引起的水润滑轴承性能变化的机制却并未给出精确阐释。同时，以往的研究对象都是基于物理模型为单一衬层的水润滑轴承，缺乏针对多衬层水润滑轴承材料的研究。因此本文作者建立了双衬层水润滑单向、双向流固耦合模型，并开展区别于传统特定材料为目标对象的研究，以一定范围的弹性模量以及泊松比作为变量，在特定工况(转速、偏心率)对水润滑轴承润滑特性影响的基础上，开展双衬层水润滑材料设计的研究，研究旨在探究不同轴瓦材料属性下水润滑轴承润滑性能的变化，揭示流固耦合作用下双衬层水润滑轴承的静态性能变化规律，并为双衬层水润滑轴承材料的选择提供一定理论依据。

1 理论分析

1.1 流体控制方程

流体流动要遵循物理守恒定律，基本的守恒定律包括质量守恒定律、动量守恒定律、能量守恒定律。同时，因为在研究水润滑轴承润滑特性时温度变化较小，故忽略不计温升的影响，也即不考虑流体、固体的能量传递。所以，不引入能量方程[21]。

质量守恒方程：

(1)

动量守恒方程：

(2)

式中：t是时间；ff是体积力矢量；ρf是流体密度；v是流体速度矢量；τf是剪切力张量，可表示为

(3)

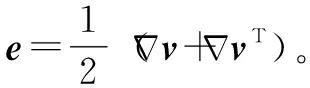
1.2 固体控制方程

固定域部分的方程由牛顿第二定律导出：

(4)

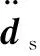
1.3 流固耦合方程

流固耦合方程也遵循最基本的守恒原则，所以在流固耦合交界面处，应满足流体的应力(τ)与位移(d)和固体应力与位移相等或守恒，也即满足以下2个方程：

τs·nf=τf·nf

df=ds

(5)

通常解决流固耦合问题时，使用直接耦合式解法。把流固控制方程耦合到同一个方程中求解，可同时求解流体和固体的控制方程：

(6)

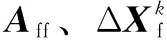
1.4 轴承的静态性能

水润滑夹心轴承的固体域为双衬层结构。因为一般的金属材料在水介质中容易发生化学反应，导致轴瓦材料的腐蚀，从而降低水润滑轴承的润滑性能。所以，水润滑轴承的轴瓦材料通常为非金属弹塑性材料，具有较大的屈服强度和泊松比。

轴承的承载能力通过对水膜上的静压积分计算[20]：

Wx=∬pcosφrdφdz

Wy=∬psinφrdφdz

(7)

摩擦力可以通过轴承区域上的摩擦应力的近似积分来表示：

(8)

摩擦功耗损失表示为

Pf=fU

(9)

式中：Wx是x方向承载力；Wy是y方向承载力；p是水膜压力；φ是任一节点的角度；r是轴承半径；z是轴向坐标；f是摩擦力；τc是Couette切向应力；h是膜厚；Pf是功率损失；U是线速度。

2 理论模型

2.1 轴承结构

夹心轴承与传统水润滑轴承的区别在于结构方面，一般水润滑轴承的衬层为单层，而夹心轴承具有双层衬层，具有增载、减阻的性能。夹心轴承的固体域由转轴及双衬层组成，规定内层为衬层1，外层为衬层2，两衬层之间固定连接。使用Solidworks软件构建模型。夹心轴承结构见图1，轴承结构参数见表1，轴承材料物理特性见表2。

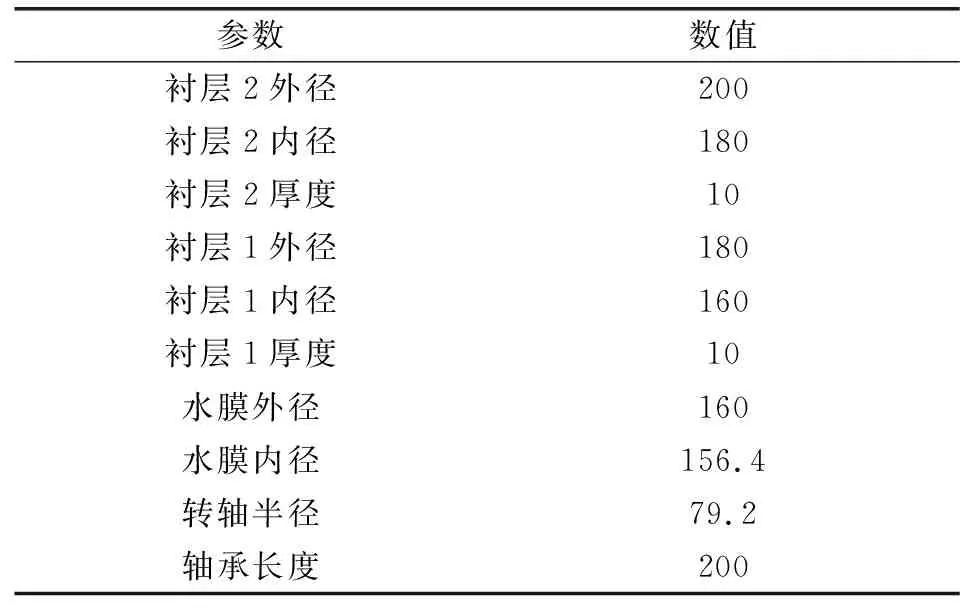
表1 水润滑夹心轴承结构参数单位：mmTable 1 Structure parameters of the water lubricated sandwich bearing Unit：mm

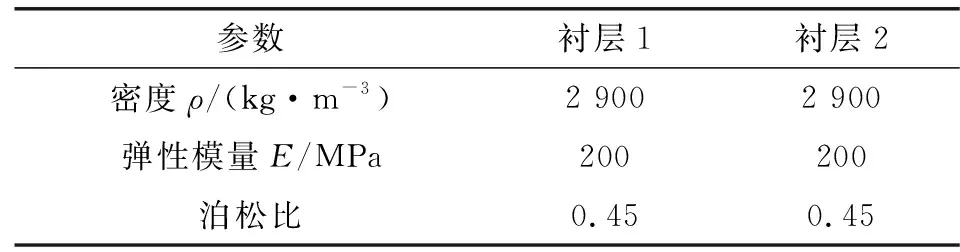
表2 水润滑夹心轴承材料物理特性Table 2 Physical properties of material of water lubricated sandwich bearing

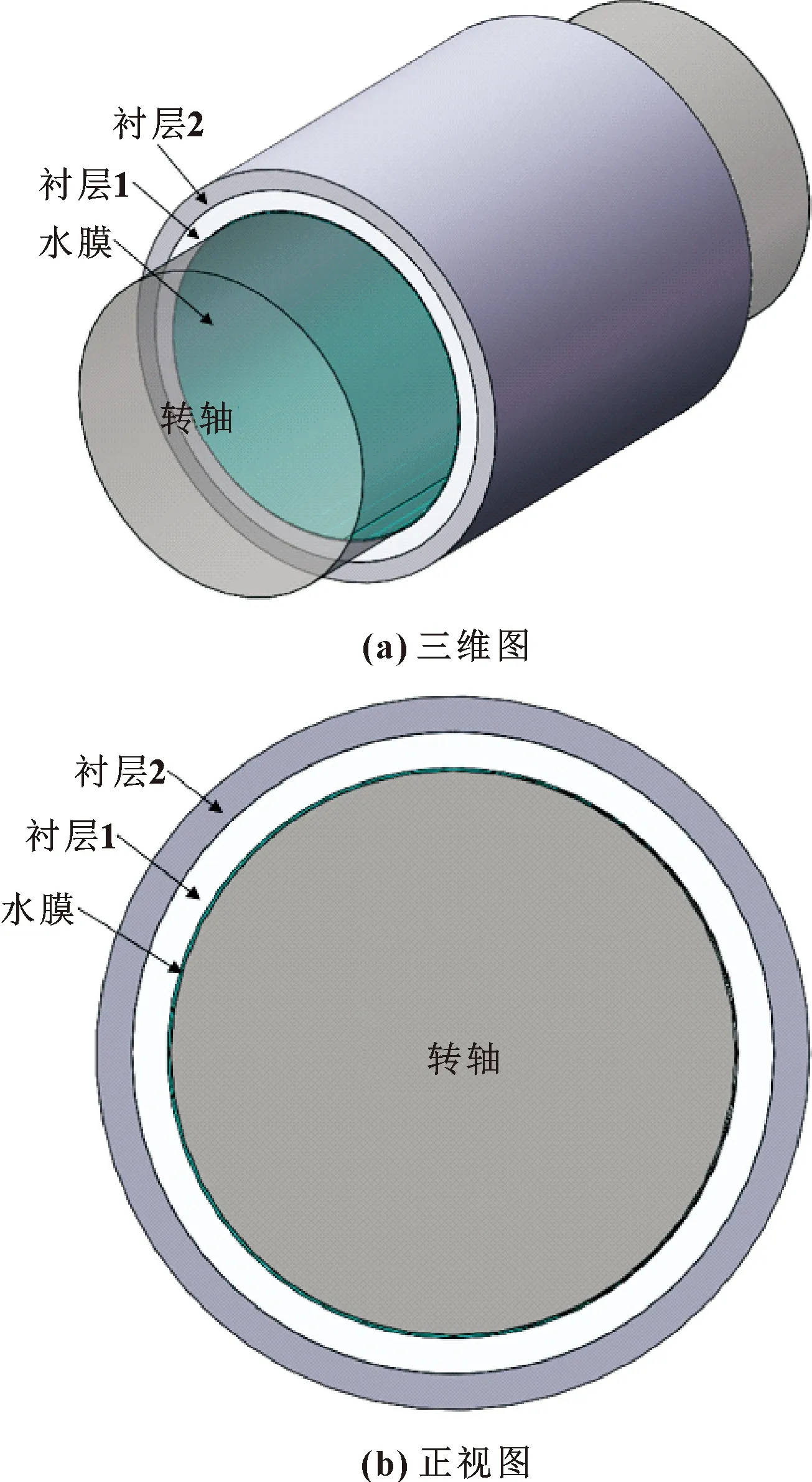
图1 水润滑夹心轴承结构Fig.1 Structure of water lubricated sandwich bearing：(a)three-dimensional diagram；(b)front view

2.2 边界条件及网格划分

转轴运行时，水膜间隙的一侧为入口端，另外一侧为出口端，并设定进出口的压力为大气压。水膜的外表面为固定面，内表面为旋转面，其转速与轴相同。双衬层结构处，衬层2外表面为固定面，衬层2内表面与衬层1外表面固定连接，衬层1内壁面为流固耦合面，双衬层端面设置为位移约束。具体边界条件如图2所示。

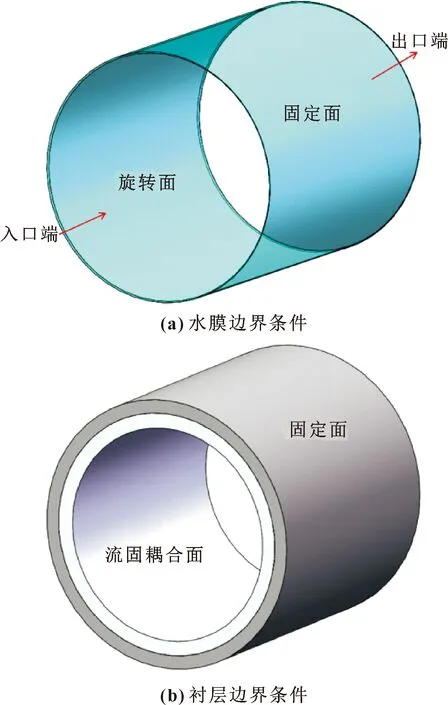
图2 边界条件Fig.2 Boundary conditions：(a)boundary conditions of water film；(b)boundary conditions of lining

流体域网格在Fluent Mesh中生成。如图3(a)所示，整体网格尺寸为3 mm，水膜出、入口两端面划分8层网格。固体域网格可在Static Structural中生成。如图3(b)和图3(c)所示，整体网格尺寸为3 mm，衬层两端面分别划分8层网格。此外，进行了网格无关性验证，在衬层1、2弹性模量均为200 MPa的情况下分别划分了整体网格尺寸为3 mm以及4 mm，比较求解结果，得出在3 mm网格情况下的水膜压力为28 620 Pa，4 mm网格情况下的水膜压力为28 740 Pa，其误差比在0.4%左右，所以为了平衡计算精度与计算时间的关系，选择了在整体网格为3 mm的情况下求解系统。如表3所示，为模型按照整体网格3 mm划分后的网格详细参数。

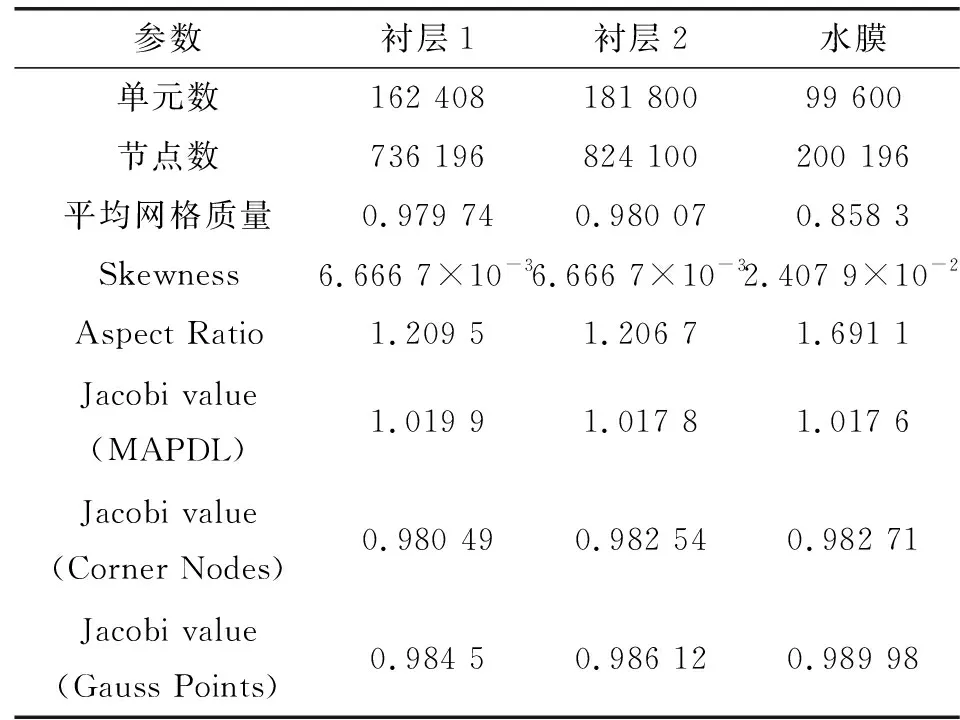
表3 网格参数Table 3 Characteristic parameters of the mesh

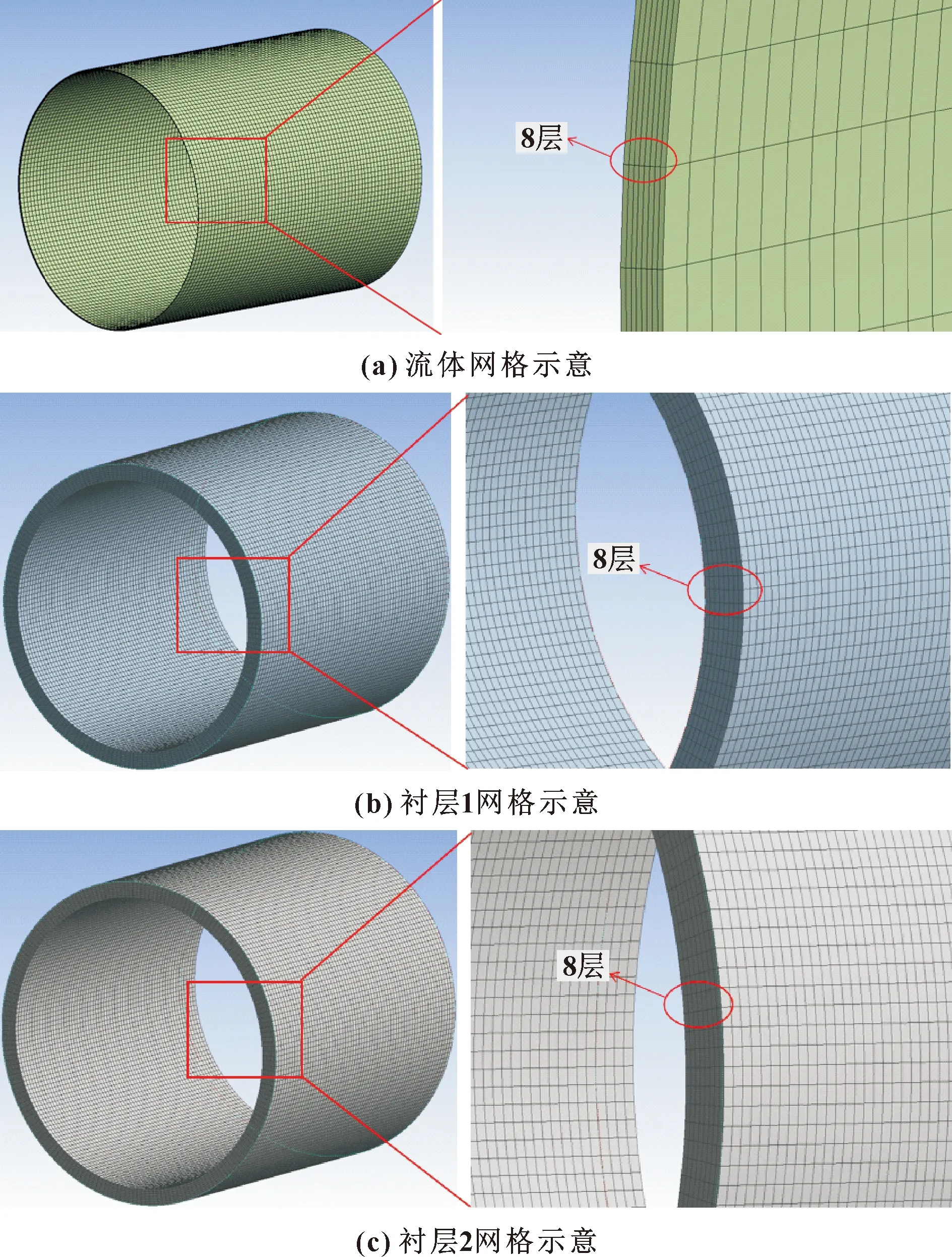
图3 网格示意Fig.3 Schematic of mesh：(a)schematic of fluid mesh；(b) schematic of liner 1 mesh；(c)schematic of liner 2 mesh

2.3 求解流程图

图4所示为系统求解流程框图。首先根据要求建立流体、固体模型并导入软件，然后划分网格并设置流体域、固体域的运行条件，进而分别求得控制方程并确定流固耦合系统结构。然后进行雷诺数的求解，之后选择模型、施加边界条件，并求解出水膜的Navier-Stokes(N-S)方程，进而判断压力的结果是否收敛。如果结果不收敛，则返回到求解雷诺数这一步骤重新求解；如果结果收敛，则证明结果达到要求，可提取衬层变形、应力、水膜压力、承载力、摩擦因数等参数，并根据参数值确定其与变量的关系图。

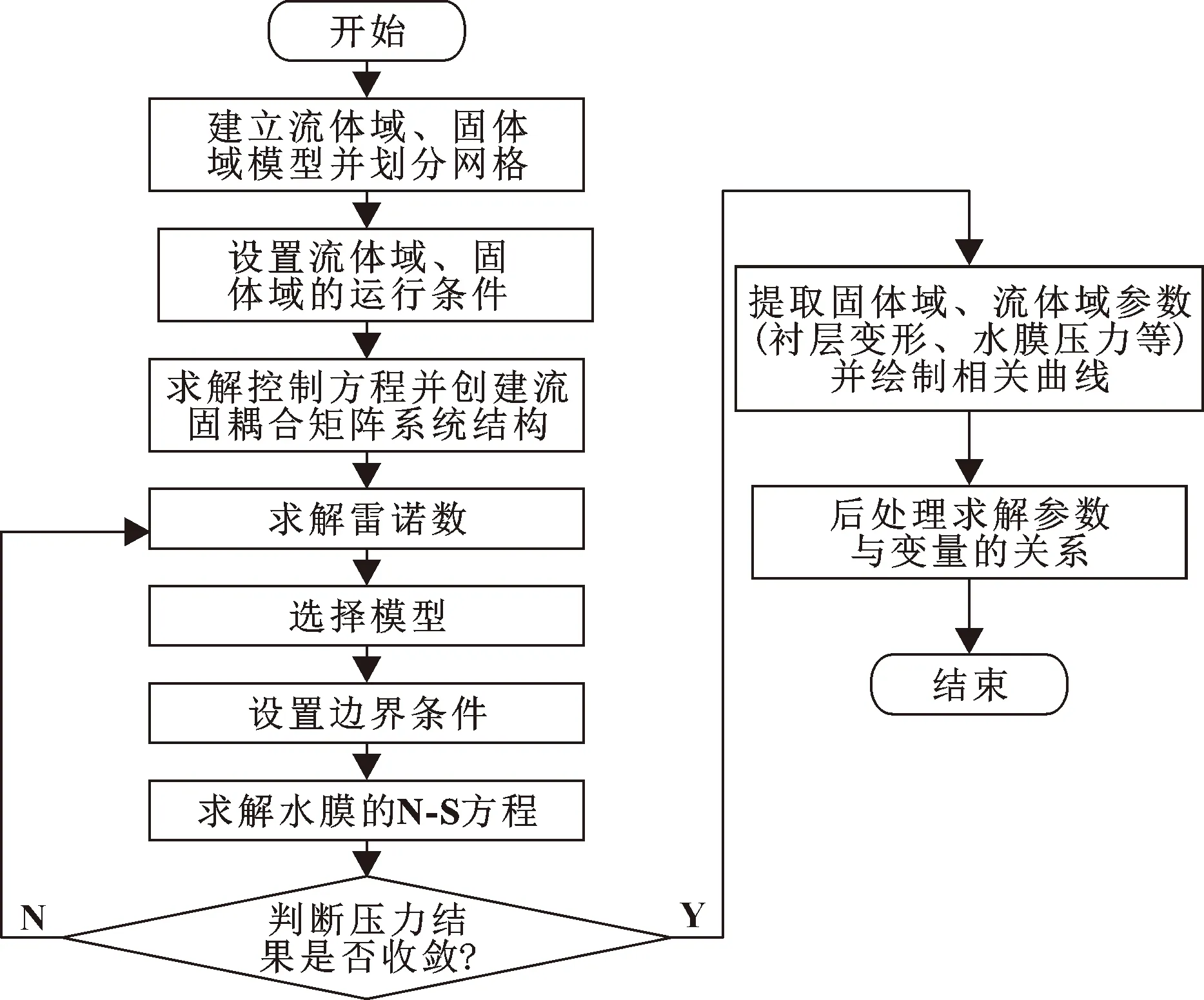
图4 系统求解流程Fig.4 Flow of system solution

3 结果与讨论

针对在一定范围内的弹性模量以及泊松比，研究了变量对于研究对象静态性能的影响，比较了水润滑夹心轴承润滑性能分别在单向、双向流固耦合情况下的区别。

3.1 弹性模量影响规律分析

因为工作环境的特殊性，水润滑轴承的轴瓦材料一般为非金属复合材料，而在实际工作中时，这类材料的弹性模量并不是常数，而是随着压力的增大而增大。文中轴承工作时的压力较小，可将弹性模量近似为常数[22]。根据复合材料的范围选择合适的变量，在工况(衬层厚度、转速、偏心率)对水润滑夹心轴承润滑性能影响的基础上，开展了轴瓦材料对轴承性能影响的研究。选择典型工况：衬层厚度均为10 mm，偏心率为0.6，转速为2 000 r/min。双衬层其他材料属性均不变，弹性模量分别取为200、400、600、800、1 000、1 200、1 400、1 600、1 800、2 000 MPa。

图5所示为在单向、双向流固耦合情况下，夹心轴承双衬层的最大变形随弹性模量的变化曲线。可见，在单向流固耦合情况下，随着弹性模量的增加，衬层1、2的最大变形都随之降低，这是因为弹性模量是表征材料抵抗弹性变形能力的物理量，其数值越大，材料刚度越大，抵抗变形的能力就越强，所以在一定应力作用下，发生的变形就越小；且在800 MPa之前，最大变形的变化率较大，800 MPa之后，最大变形的变化曲线变得平缓；同时，衬层1的最大变形始终是大于衬层2，这是因为衬层1与转轴直接接触，会产生更大的变形；双向流固耦合情况下的衬层最大变形随弹性模量的变化趋势与单向情况下一致。

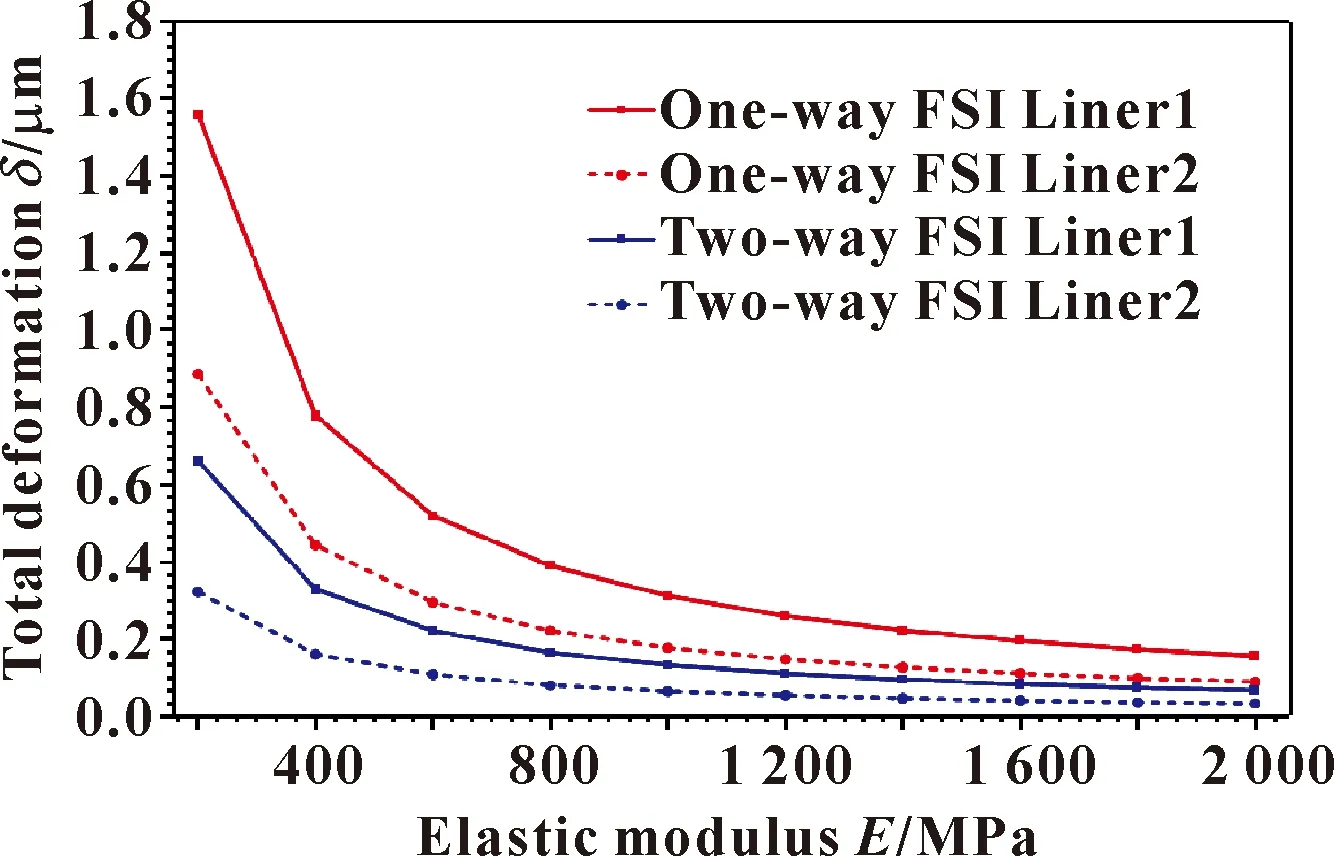
图5 最大变形随弹性模量的变化Fig.5 Variation of maximum deformation with elastic modulus

图6所示为在单向、双向流固耦合情况下，夹心轴承双衬层的最大应力随弹性模量的变化曲线。可见，单向流固耦合情况下，随着弹性模量的增加，衬层1、2的最大应力都不发生变化，衬层1始终为0.016 706 MPa，衬层2始终为0.015 42 MPa。这是因为应力是单位面积所受的力，所以在相同载荷的同一材料结构中，应力分布与弹性模量无关；而在双向流固耦合情况下，随着弹性模量的增加，衬层受到的最大应力会发生微小的变化，其值会在一定范围内上下波动。

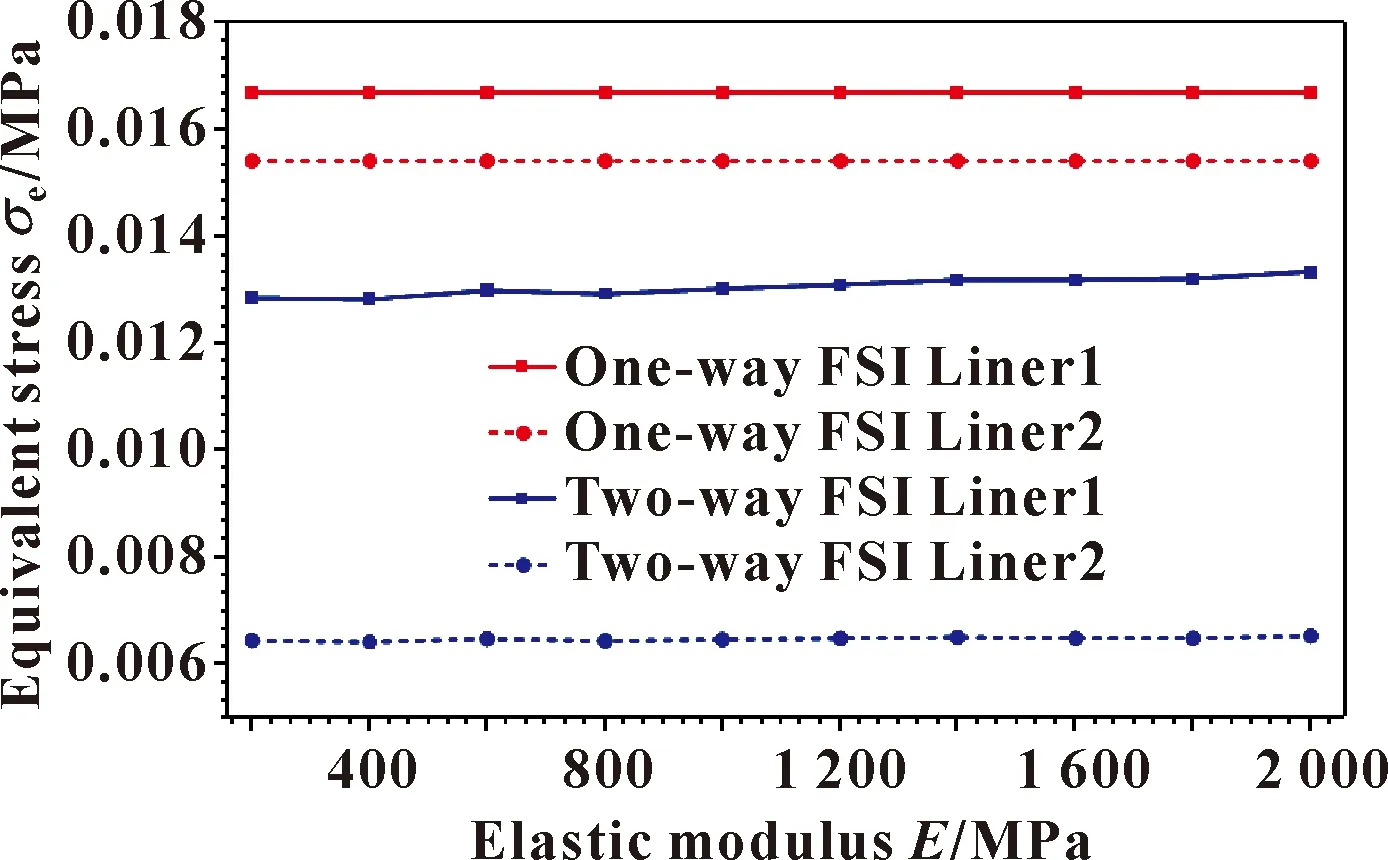
图6 最大应力随弹性模量的变化Fig.6 Variation of equivalent stress with elastic modulus

图7给出了双向流固耦合情况下600、1 200、1 600 MPa 3组弹性模量下的水膜压力3D云图。从3组水膜云图上来看，都存在正、负2个集中承载区域，红色显示为正压承载区域，蓝色为负压承载区域。从数值上来看，水膜压力并不随着衬层弹性模量的变化而发生较大的变化；从云图轮廓上来看，随着衬层弹性模量的变化，水膜的承载区域和整个水动力润滑区域不发生改变，压力中心的位置发生微小变化。

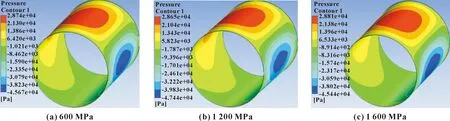
图7 不同弹性模量下水膜压力云Fig.7 Pressure contours of water film under different elastic modulus：(a)600 MPa；(b)1 200 MPa；(c)1 600 MPa

图8所示为在单向流固耦合与双向流固耦合情况下水膜周向压力的对比曲线。根据图7得出的结论，双向流固耦合情况下衬层弹性模量的变化并不会引起水膜压力的过大变化，也不会使得水膜承载区域与水动力润滑区域的向前或向后的变化，所以选取了双向流固耦合中双衬层弹性模量均为200 MPa的水膜压力，提取出周向压力分布，然后提取了同一转速下单向流固耦合的水膜周向压力分布，将二者做出对比。由图8可以看出，在不同的情况下，水膜最大正压基本相等，但单向流固耦合情况下产生了更大的水膜负压，而且水膜的压力正负峰值所处在轴承的位置并不一致；同时，相比于单向流固耦合下的水膜压力分布，双向流固耦合下的压力峰值之间具有更小的带宽。

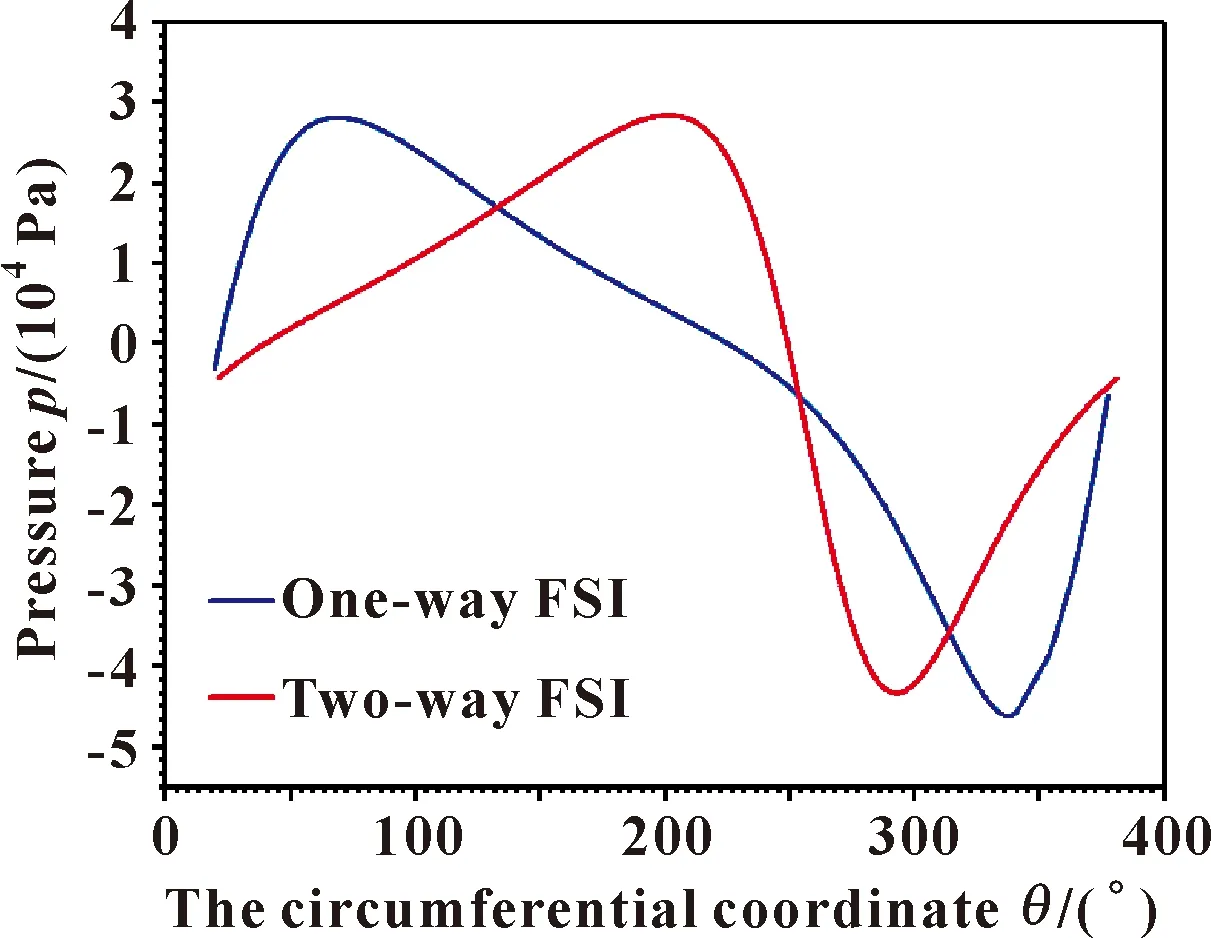
图8 水膜周向压力变化Fig.8 Variation of water film pressure on the circumferential direction

图9所示为在双向流固耦合情况下，轴承承载力、水膜最大压力随弹性模量变化曲线。可知，随着双衬层弹性模量的逐渐增大，水膜承载力的变化并不明显，其数值处于一个稳定值的上下波动范围内。所测的弹性模量范围内，水膜承载力的最大值为983.77 N，最小值为968.30 N，最大差值为15.47 N，差值比为1.6%左右。因此，水膜承载力随弹性模量的变化规律并不显著。同时，随着弹性模量的变化，水膜的最大压力同样不发生较大的变化，最大压力值为28 810 MPa，最小压力值为28 620 MPa，最大差值为190 MPa，差值比为0.7%左右。因此，水膜受到的最大压力随衬层弹性模量的变化规律也不显著。

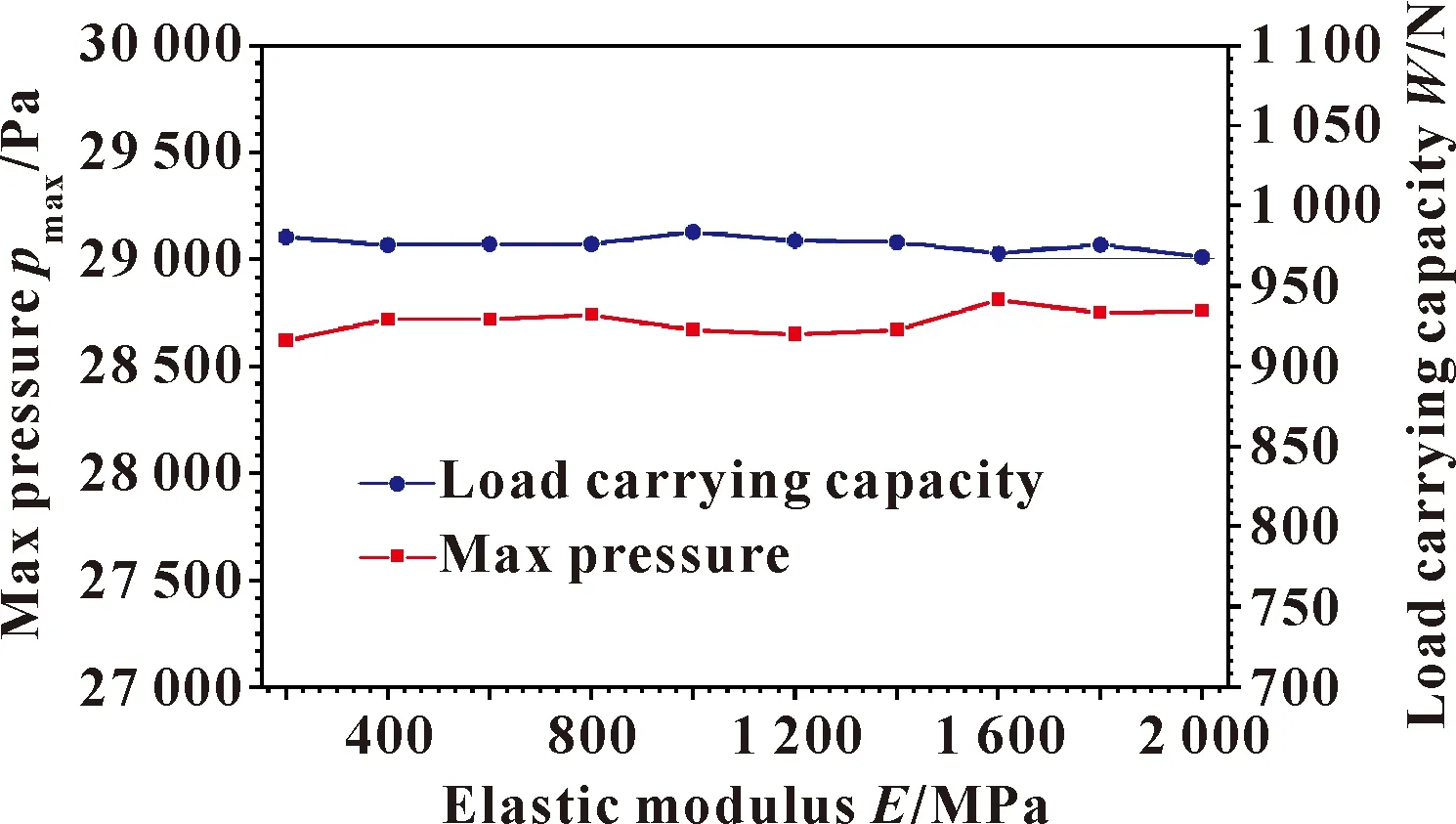
图9 双向流固耦合水膜承载力和最大压力随弹性模量的变化Fig.9 Variation of load carrying capacity and max pressure with elastic modulus in two-way FSI

表4显示了在10组不同弹性模量下双向流固耦合水润滑模型的特征参数。水润滑夹心轴承衬层弹性模量的变化并不会引起轴承承载能力和水膜最大压力的变化，而摩擦因数在一定范围内上下波动；同时承载区域和整个水动力润滑区域不发生改变，压力中心的位置发生微小的变化。

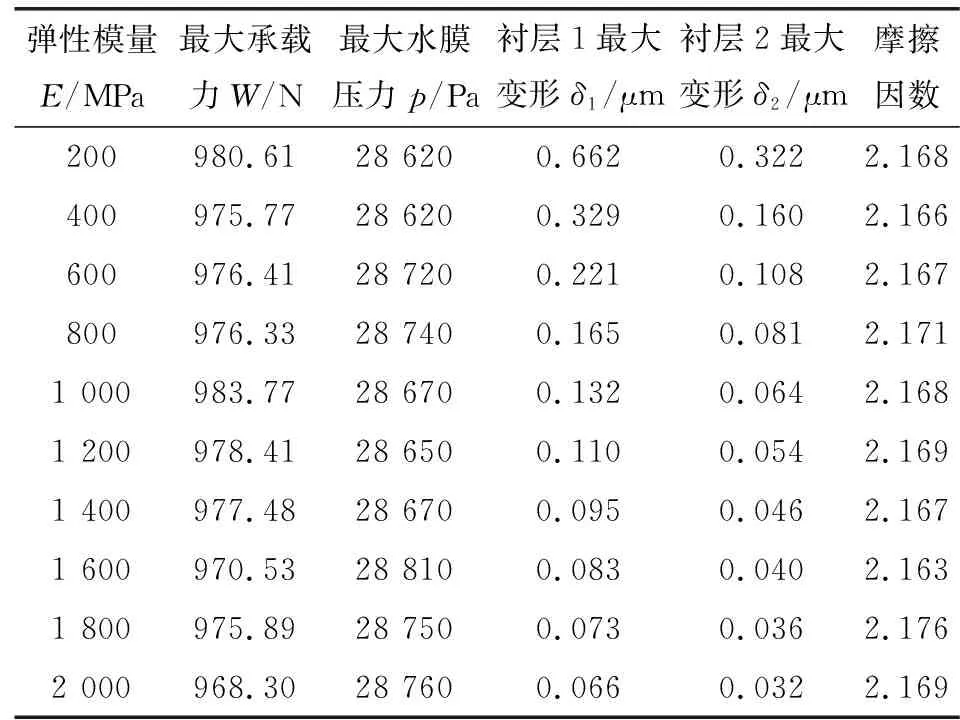
表4 不同弹性模量下双向流固耦合水润滑轴承模型特征参数Table 4 Characteristic parameters of water lubricated bearing model of two-way FSI under different elastic modulus

3.2 弹性模量之比影响规律分析

双衬层结构弹性模量均取相同的数值可以得到静态性能随之改变的基本规律。但实际上，双衬层结构的材料属性往往并不相等，所以分析不同数值产生的规律变化也尤为重要。对此，提出弹性模量之比的概念来探究水润滑夹心轴承的润滑特性的变化。规定某一层衬层弹性模量数值恒定不变，同时等比例地增加另外一层衬层的弹性模量数值，旨在探究夹心轴承的润滑性能随弹性模量之比的变化规律，为水润滑夹心轴承的选材提供理论依据。

3.2.1 衬层2与衬层1弹性模量之比的影响

根据上述分析，得出了双衬层均在200 MPa处最大变形最为明显，所以以此数据为基础，设置衬层1的弹性模量为固定200 MPa，等比例地增加衬层2的弹性模量，进行了仿真分析。为了更清楚地厘清二者的关系，需要在更大量级上计算数据，这样对图线变化规律的解释更有说服力。因此，衬层1弹性模量E1恒定为200 MPa，E2分别取400、800、1 200、1 600、2 000、20 000 MPa进行仿真分析。

图10所示为弹性模量之比与衬层最大变形的关系曲线。可以看出，当E2/E1的数值小于等于10时，随着弹性模量之比E2/E1的增大，衬层1、2所受的最大变形均在明显减小(说明在小比值情况下，衬层的最大变形受到的影响较为明显)；而当E2/E1的数值在10以上时，衬层1、2受到的最大变形不发生明显的变化(说明大比值情况下，衬层的最大变形的变化并不明显)。当E1的数值不变，而E2等比例增大并逐渐增大到无限大时，此时衬层2的刚度无限大，可将衬层2等效为衬套，故此时双衬层结构也就变为了单衬层结构。所以整个过程(即E2/E1在数值上等比例增大的过程)也可等效为双衬层轴承逐渐变化为单衬层轴承的过程。故整个过程可以解释为：由于衬层1的弹性模量数值恒定为200 MPa，衬层2的弹性模量逐渐增加的过程中，增加的数值与衬层1的数值200 MPa在同一量级时，最大变形会发生明显的变化，但当E2增加的数值远远大于200 MPa时，最大变形不发生较大改变。

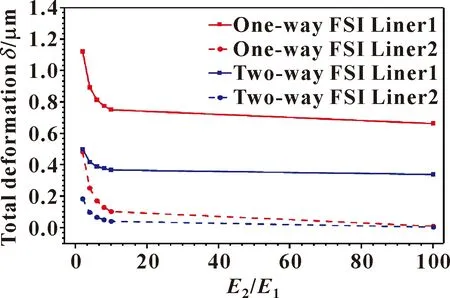
图10 最大变形随弹性模量之比E2/E1的变化Fig.10 Variation of maximum deformation with the ratio of elastic modulus E2/E1

图11所示为弹性模量之比E2/E1与衬层最大应力的关系曲线。可以看出，当E2/E1的数值小于等于10时，随着弹性模量之比E2/E1的增大，衬层1所受的最大应力在明显减小，衬层2受到的最大应力在明显增大；而当E2/E1的数值在10以上时，衬层1、2受到的最大应力不发生明显的变化。

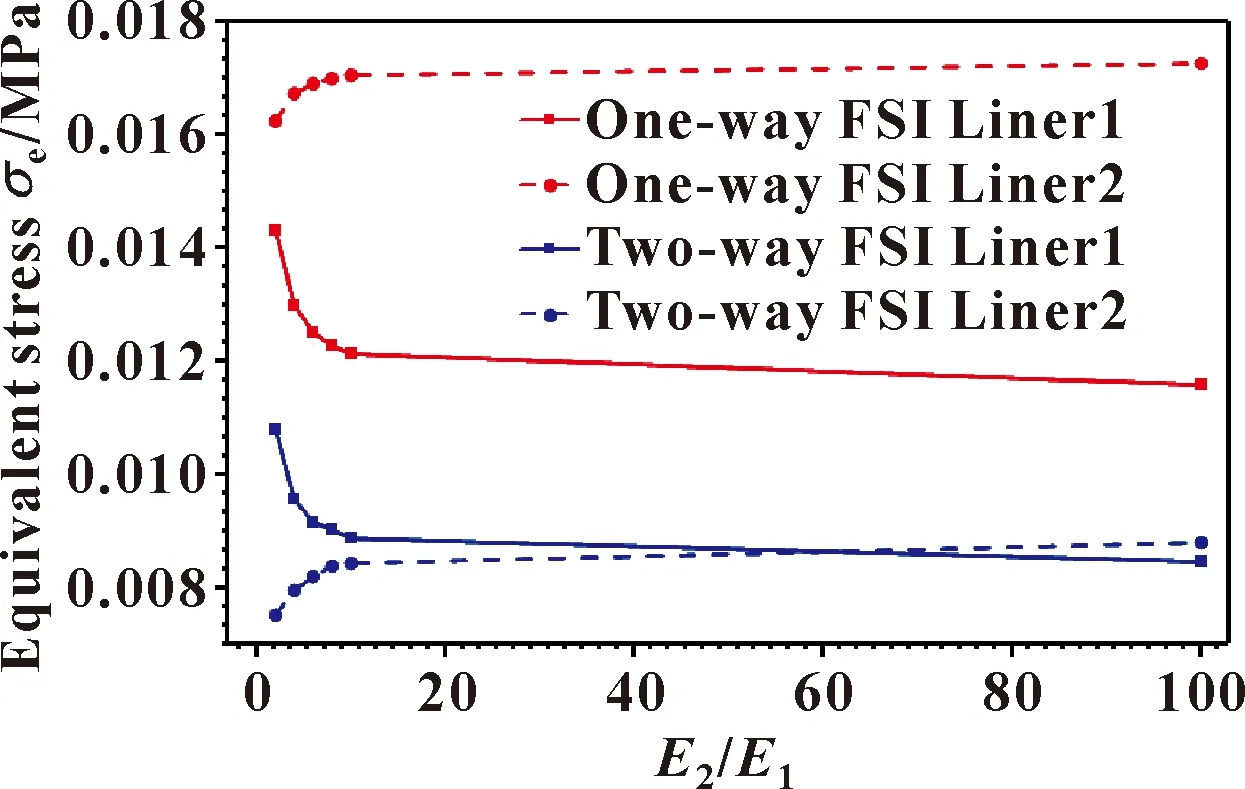
图11 最大应力随弹性模量之比E2/E1的变化Fig.11 Variation of equivalent stress with the ratio of elastic modulus E2/E1

表5显示了在不同的弹性模量之比E2/E1下双向流固耦合水润滑模型的特征参数。可见，水润滑夹心轴承衬层弹性模量之比的变化并不会引起轴承承载能力和水膜最大压力的过大变化，而摩擦因数数值在微小的范围内波动。

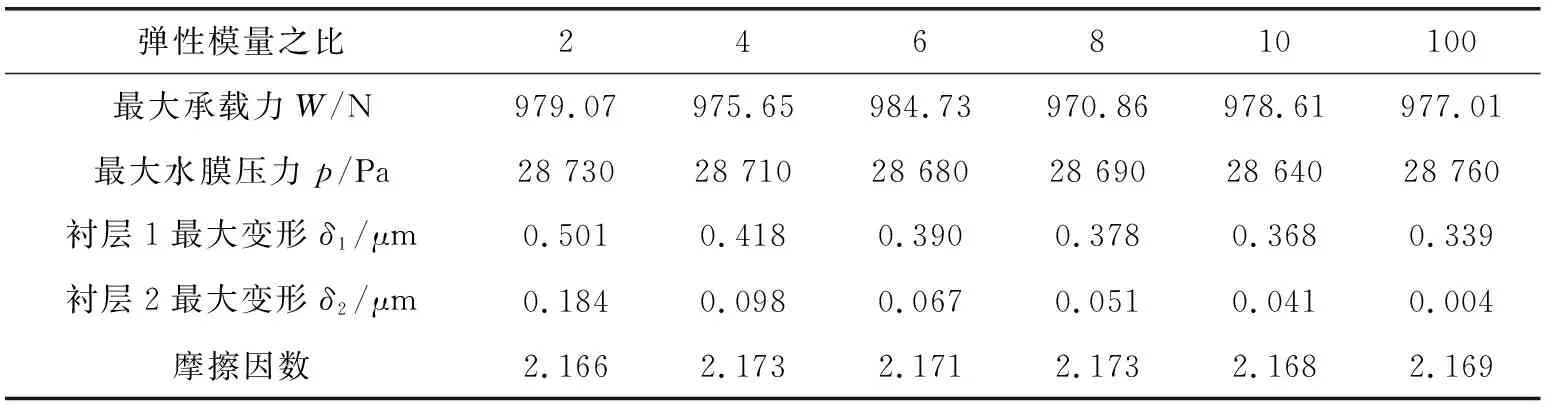
表5 不同弹性模量之比E2/E1下双向流固耦合水润滑轴承模型特征参数Table 5 Characteristic parameters of water lubricated bearing model of two-way FSI under different the ratio of elastic modulus E2/E1

3.2.2 衬层1与衬层2弹性模量之比的影响

同样地，设置衬层2的弹性模量固定为200 MPa，等比例地增加衬层1的弹性模量，即E1分别取值400、800、1 200、1 600、2 000、20 000 MPa，进行了仿真分析。

图12所示为弹性模量之比E1/E2与衬层最大变形的关系曲线。可以看出，当E1/E2的数值小于等于10时，随着弹性模量之比E1/E2的增大，衬层1、2所受的最大变形均在明显减小，说明在小比值情况下，衬层的最大变形受到的影响很明显；当E1/E2的数值在10以上时，衬层1、2受到的最大变形同样发生较为明显的变化，但变化速率并没有小比值情况下快。当保持E2的数值为200 MPa不变，而E1等比例增大并逐渐增大到无限大时，此时衬层1的刚度无限大，此时可将衬层1等效为“浮环”，整个系统等效类似为“浮环轴承”，也即衬层1作为“浮环”将轴颈与衬层2(轴瓦)分隔开来。所以当E1增加的数值与E2恒定不变的数值在量级上差别不大时，最大变形会以强烈的趋势下降；而当E1增加的数值与E2恒定不变的数值在量级上相差较大时，此时E1远大于E2(E2可忽略)，衬层1、衬层2的数值仍然以较为强烈的趋势下降，但下降速率没有小比值情况下大。

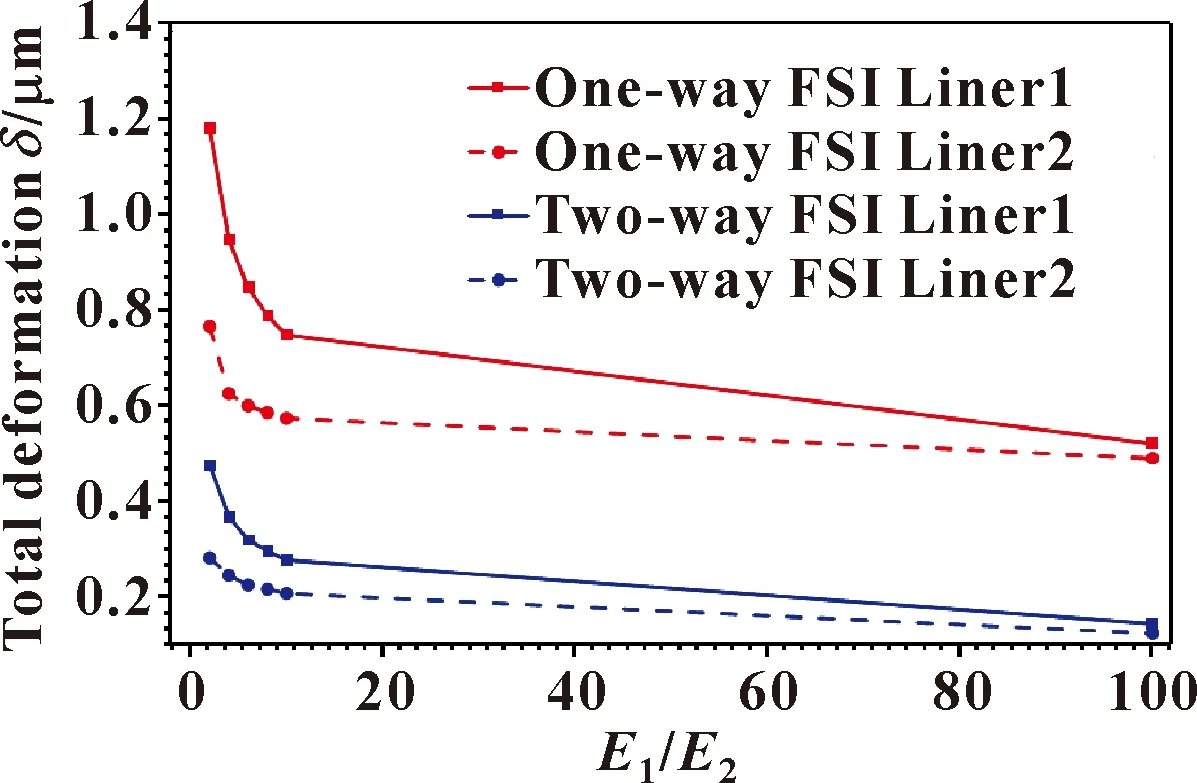
图12 最大变形随弹性模量之比E1/E2的变化Fig.12 Variation of maximum deformation with the ratio of elastic modulus E1/E2

图13所示为弹性模量之比E1/E2与衬层最大应力的关系曲线。可以看出，当E1/E2的数值小于等于10时，随着弹性模量之比E1/E2的增大，衬层1所受的最大应力在明显增大，衬层2受到的最大应力在明显减小；当E1/E2的数值在10以上时，衬层1受到的最大应力同样发生明显的变化，衬层2受到的最大应力变化不明显。

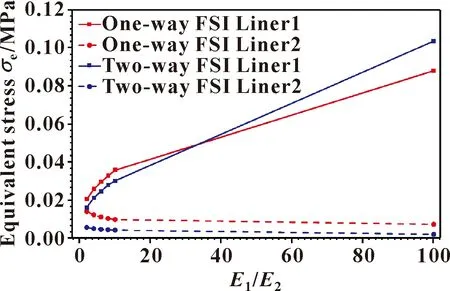
图13 最大应力随弹性模量之比E1/E2的变化Fig.13 Variation of equivalent stress with the ratio of elastic modulus E1/E2

图14(a)、(b)给出了双向流固耦合情况下，E2/E1的数值等于10、100时的水膜压力3D云图。图14(c)、(d)给出了E1/E2的数值等于10、100时的水膜压力3D云图。从数值上来看，水膜压力并不随着衬层弹性模量之比的变化而发生较大的变化；从云图轮廓上来看，随着衬层弹性模量之比的变化，水膜的承载区域和整个水动力润滑区域不发生改变，压力中心的位置会有微小的变化。

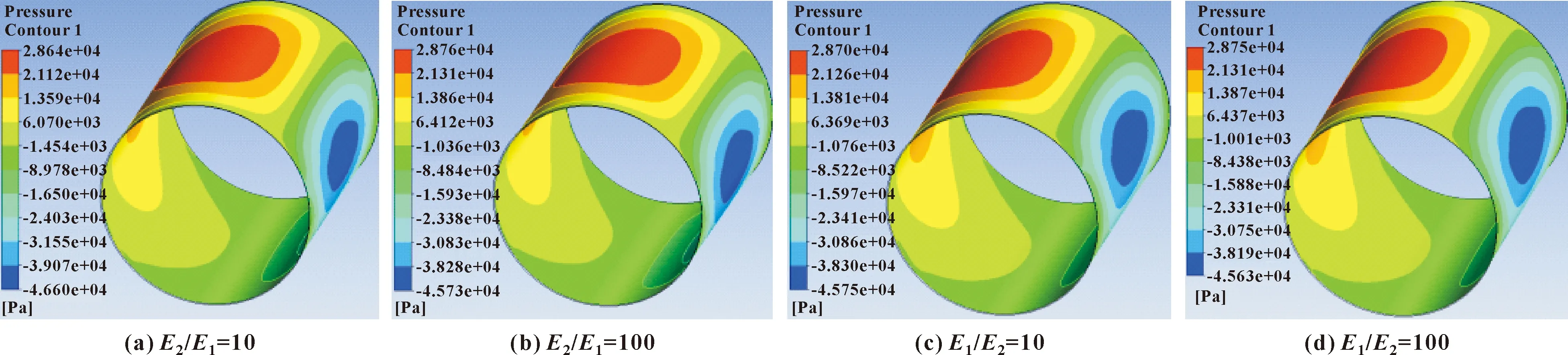
图14 不同弹性模量之比下的水膜压力云图Fig.14 Pressure contours of water film under different ratio of elastic modulus：(a)E2/E1=10；(b)E2/E1=100：(c)E1/E2=10；(d)E1/E2=100

图15所示为水膜承载力以及水膜最大压力与弹性模量之比的变化关系。比较两图，在同一比值下，水膜的承载力数值、最大压力数值在2种情况下(E2/E1、E1/E2)几乎相等；承载力、最大压力随着弹性模量的变化规律也不明显，数值上也几乎不发生变化。可以推测，水膜的承载力、压力与衬层弹性模量之比并无关系。

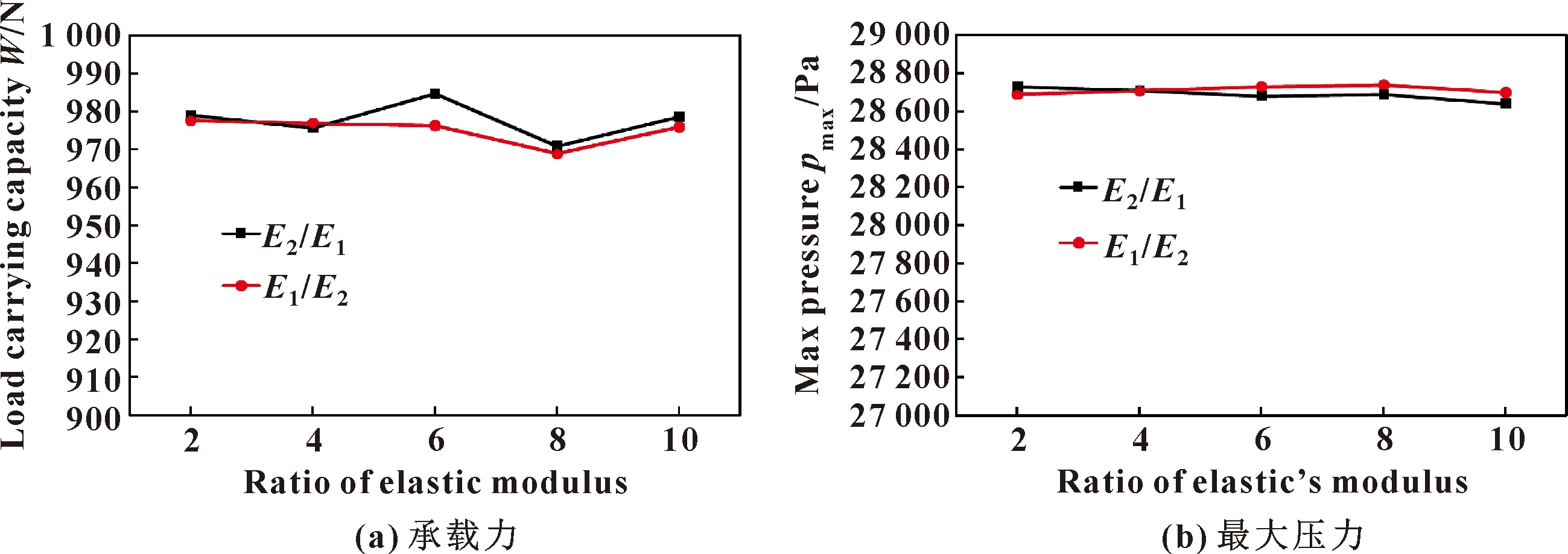
图15 水膜特性随弹性模量之比的变化Fig.15 Variation of water film properties with the ratio of elastic modulus：(a)load carrying capacity；(b)max pressure

表6显示了在不同的弹性模量之比E1/E2下双向流固耦合水润滑模型的特征参数。可见，水润滑夹心轴承衬层弹性模量之比的变化并不会引起轴承承载能力和水膜最大压力的过大变化，而摩擦因数发生微小变化。

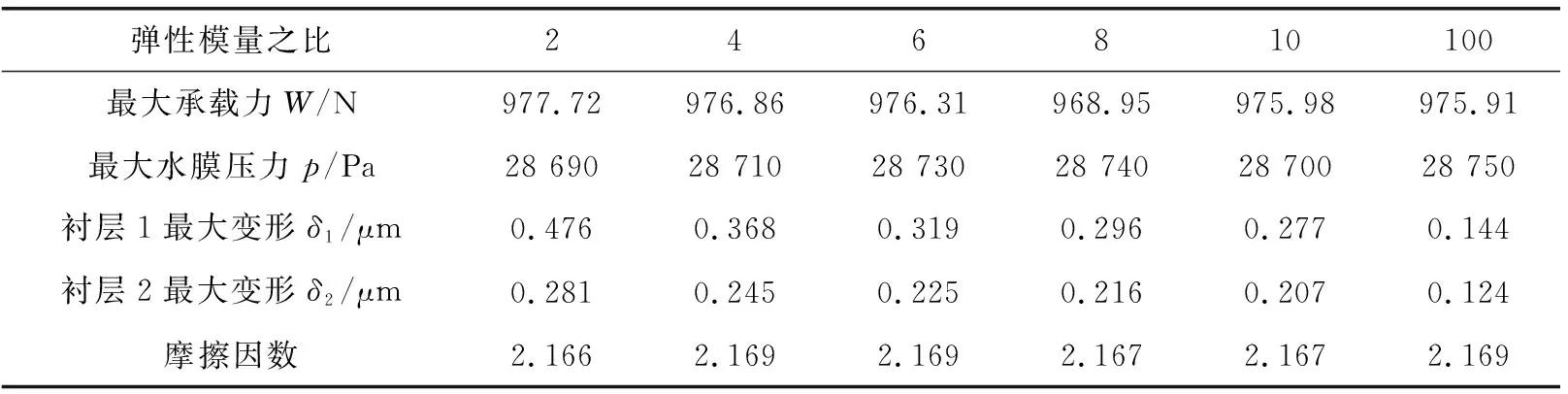
表6 不同弹性模量之比E1/E2下双向流固耦合水润滑轴承模型特征参数Table 6 Characteristic parameters of water lubricated bearing model of two-way FSI under different the ratio of elastic modulus E1/E2

3.3 泊松比影响规律分析

作为非常重要的材料属性参数，泊松比的变化同样对轴承的性能有一定影响，实验设定一定范围内的泊松比按规律变化，探究其对静态性能产生的影响。

图16所示为水润滑夹心轴承双衬层最大变形与泊松比的关系。可知，衬层1的最大变形总是大于衬层2的最大变形，随着泊松比的增加，衬层1、衬层2最大变形几乎呈线性减小，且两衬层变形差值在不断减小；衬层2的最大变形在泊松比达到0.42后几乎不发生变化。图17所示为水润滑夹心轴承双衬层最大应力与泊松比的关系。可知，衬层1受到的最大应力始终大于衬层2；且随着泊松比的增加，衬层1、衬层2的最大应力几乎呈线性减小，但泊松比达到0.42后，衬层2最大应力下降速率变得平缓。

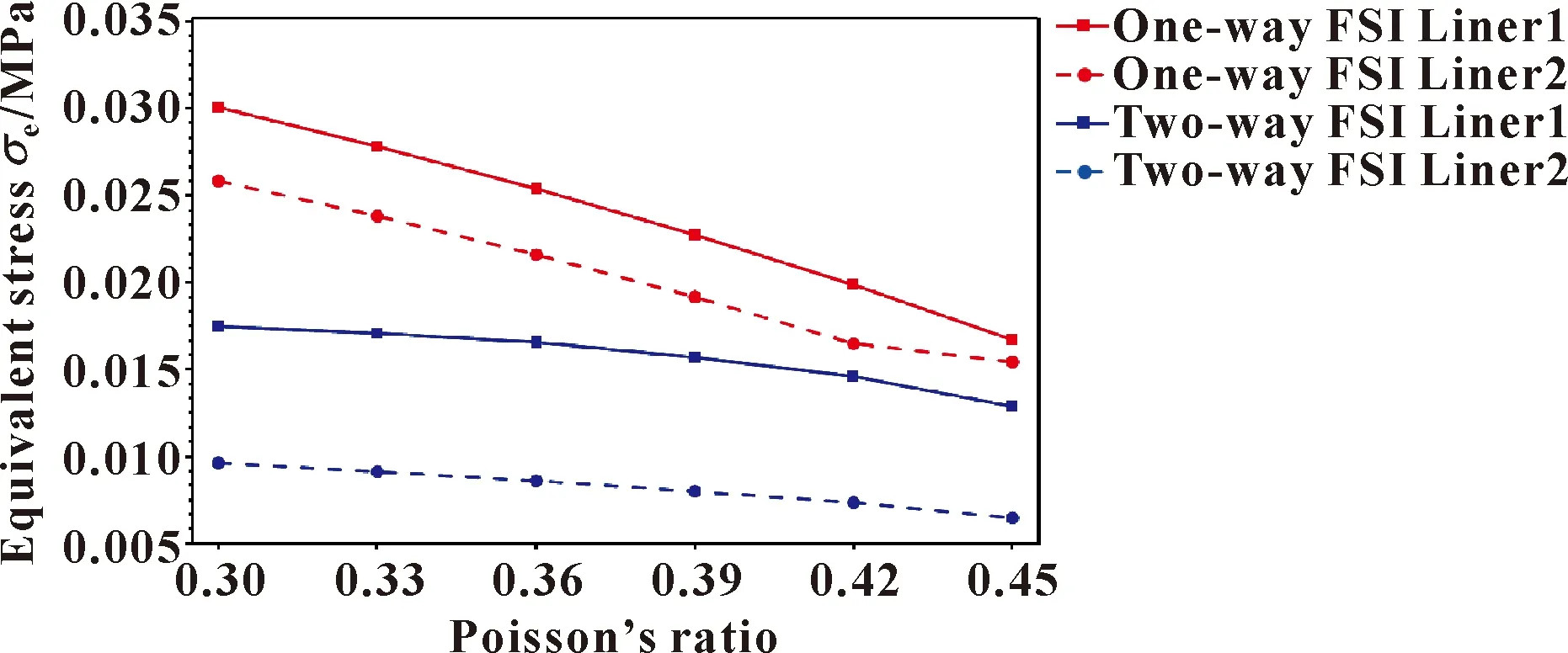
图17 最大应力随泊松比的变化Fig.17 Variation of equivalent stress with Poisson’s ratio

表7显示了在不同泊松比下双向流固耦合水润滑轴承模型的特征参数。可见，水润滑夹心轴承衬层泊松比的变化并不会引起轴承承载能力和水膜最大压力过大的变化，而摩擦因数也只在微小的范围内波动，整个流体域的静态性能变化不明显，承载区域和压力边界变化不大。

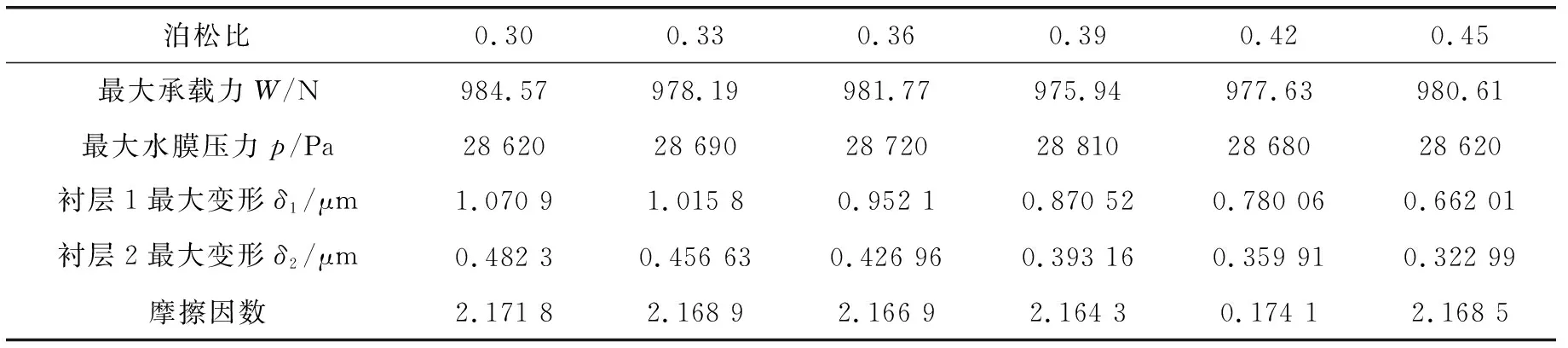
表7 不同泊松比下双向流固耦合水润滑轴承模型特征参数Table 7 Characteristic parameters of water lubricated bearing model of two-way FSI under different Poisson’s ratio

4 结论

为研究在一定材料属性范围内水润滑轴承润滑性能的变化规律，分别构建了夹心轴承单向、双向流固耦合模型，设置衬层1、衬层2不同的材料参数，开展了材料属性的变化对夹心轴承润滑性能影响的研究，研究了弹性模量、泊松比对轴承承载、水膜压力、衬层变形等静态性能参数的影响规律，探究了夹心轴承的润滑机制。得到了如下结论：

(1)衬层1、2弹性模量相同的情况下，在2种流固耦合情况中，随着弹性模量的增加，衬层1、2的最大变形都随之降低，最大应力保持不变。且应力与弹性模量之间满足胡克定律；但不论是衬层1还是衬层2，其在双向流固耦合情况下得出的变形、应力均小于单向流固耦合情况下的变形、应力。水膜压力、承载力、摩擦因数均不随弹性模量的变化发生较大改变，且水膜承载区域与整个润滑区域并不会发生向前或向后的移动。

(2)在2种流固耦合情况中，衬层2和衬层1弹性模量比值在小量级情况下，随着弹性模量之比的增加，衬层1、2最大变形都随之迅速降低，衬层1所受的最大应力随之迅速降低，衬层2受到的最大应力随之迅速增大；衬层2和衬层1弹性模量比值在大量级情况下，随着弹性模量之比的增加，衬层1、2最大变形也降低但降低速率极为平缓，衬层1、2最大应力变化也极为平缓；同样地，水膜压力、承载力等静态性能也不发生较大的变化，与在改变弹性模量的情况下类似。

(3)在2种流固耦合情况中，衬层1和2衬层弹性模量比值在小量级情况下，随着弹性模量之比的增加，衬层1、2最大变形随之迅速降低，衬层1所受的最大应力随之迅速增大，衬层2受到的最大应力随之降低；衬层1和2衬层弹性模量比值在大量级情况下，衬层1、2受到的最大变形同样发生较为明显的变化，但变化速率并没有小比值情况下快，衬层1受到的最大应力同样发生明显增大趋势，衬层2受到的最大应力变化不明显；此外，流体域的性能变化也不明显。

(4)在2种流固耦合情况中，衬层1、衬层2的最大变形、最大应力均随着泊松比的增大而减小，但流体区域的性能不发生显著的变化。