电动汽车接入配电网不平衡负荷数据渐进学习方法

董华忠，蒋达飞，尹维波

（国网冀北电力有限公司唐山供电公司，河北唐山 063000）

近几年，随着电动汽车充电时间不断缩短，续航能力不断提高，充电设施不断完善，城市中电动汽车的数量也在不断增加。随着V2G 模式下的分布式光伏发电及电动汽车大量接入到城市配电网络，配电网络中分布式发电的比例将会大大增加。在大规模的分布式电源接入后，将不能满足电力系统运行可靠性和电能高品质要求。当数据不均衡时，一般的分类算法往往会对大部分的类进行预测，从而使其对少数类的学习效率降低。非平衡学习方法包含了数据层次和算法层次两个层次。在算法层次上，调整决策阈值，通过调整不同类的代价来消除不平衡。数据层级的解决办法具有算法上的独立性，采用不同的重新取样技术来均衡类别的分配。数据采样技术是通过增加少数类别取样，即过采样或欠采样，以使数据类别分布均衡。由于欠采样会去除一部分训练样本，其缺点是会导致信息的损失，同时也会缩短训练的时间[1]。过采样可以通过对少数类别取样进行拷贝或填充，虽然可以降低类别失衡，但是也导致了更多边际或噪音样例的出现[2]。针对这一问题，提出了电动汽车接入配电网不平衡负荷数据渐进学习方法。

1 电动汽车接入配电网不平衡负荷变化规律

单向无序充电是一种随意的充电模式，即插即用，是最普遍的电动汽车充电方法。在无秩序状态下，使用者的行为具有很大的随机性，交通习惯与驾驶特征对电动汽车充电时间有显著的影响[3]。在给定电力系统初始负载和电力系统容量的前提下，利用蒙特卡洛方法分析了电力系统一日的电力需求量，并对其在不同的电力系统中的应用进行了研究。因此，对电动汽车接入对配电网原始负荷变化影响作用进行了定量研究[4]。

电力负荷计算以天为单位，时间间隔以分钟为单位，计算电动汽车接入配电网的总充电功率，公式为：

式中，Wn,t表示第n辆电动汽车在第t时刻的等效功率；N表示电动汽车接入配电网的总数[5]。

通过计算电动汽车的总充电功率，仿真充电负载曲线，如图1 所示。

由图1 可知，电动汽车接入配电网时，在一天内存在两个高峰期，分别是9:00 和20:00。电动汽车的充电负荷会使一日的配电网负荷增大，而配电网的峰值与原来的峰值电压叠加，使峰谷差增大，从而使配电网的负荷变得更多[6-7]。按照使用者的习惯，电动汽车在下班后的这段时间开始充电，也就是传统的峰值时段，这时段的配电网呈现一种“峰上加峰”负荷状态，而当电动汽车充电负荷较低时，则会出现峰谷差[8-9]。

在负荷特征分析中，峰谷差率是一个非常重要的参数，其定义如下：

式中，q′表示峰值负荷；q″表示谷值负荷[10]。由于不同时刻，电动汽车充电需求不同，所以在无序充电状态下电网峰谷负荷也会增加，这就导致了配电网需要及时调整发电机容量，从而产生了不平衡负荷。

2 配电网不平衡负荷数据渐进学习

2.1 不平衡负荷数据合成

不平衡负荷数据合成的目的是通过添加合成样例，平衡少数类训练信息。将少量的类作为“种子”，采用数据综合的方法进行合成[11]。为了简明合成定义，所提及的属性值栏位是一些例子中的一组属性值。在产生合成数据时，根据以下方式合成实例的各属性值：在标准类型的属性中，数据合成算法从这个属性的数值分布中随机选取一个类型的数值。

设属性b为标注的属性，其值域范围为{b1,b2,…,bm}，每个属性值出现频率分别为f1,f2,…,fm。利用随机数发生器确定一个在（0，1）范围内的均匀分布随机数，其中0 是原始数据，1 是合成数据，而合成数据则按类别标示[12-13]。从中选取合成样例的属性值，保证合成数据属性概率分布与实际分布情况一致。

对连续属性，用数据合成方法，利用其属性分布的均值和方差，随机产生属性值[14]。根据上述方法，生成各属性的数值，由此可以获得一个如图2 所示的合成样例。

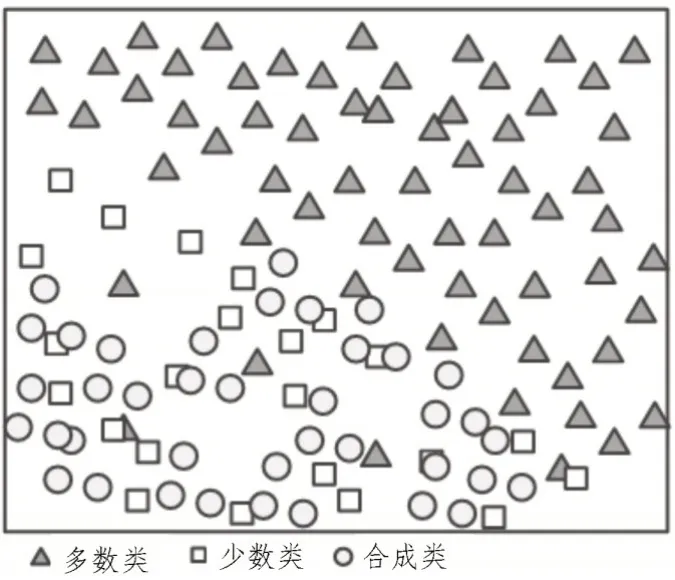
图2 合成样例示意图

由图2 可知，在数据合成处理完成后，对合成数据进行了训练，并加入了一些合成数据，在某种程度上平衡了数据分配。

2.2 不平衡负荷数据渐进学习

结合上述合成的样例，采用渐进学习方式，学习不平衡负荷数据，详细步骤为：

步骤1：将无标记数据按照一定时间顺序输入到一个线性分类器中，由于该分类器存在着很大的不平衡性，所以一般将该类型的数据流设置为稀有类型[15]；

步骤2：在非对称访问策略的基础上，利用线性分类器对未标记的不平衡数据进行排序，确定所需标记的样本；

步骤3：在非对称更新策略的基础上，采用了基于错误预测的标注数据，改进了线性分类器，同时引入了二次抽样信息，以优化学习效果[16-18]。

非对称更新策略的步骤如下：

步骤3.1：获取错误预测有标签数据，为了获取错误预测的有标签数据，需先计算置信度，公式为：

式中，η表示分类器学习率；δmax表示样本错误分类最大概率；λ表示正则化系数。

根据置信度计算结果，计算当前配电网不平衡负荷数据的非对称访问参数，如下：

式中，| |Lt表示线性分类器对当前数据预测的距离。

在确定非对称访问参数后，获取采样值。针对不同类别样本设定的采样系数，通过如下公式进行采样：

式中，qt表示非对称访问参数；φ+表示正类预测的采样系数；φ-表示负类预测的采样系数。通过该采样方式，获取错误预测的有标签数据。

步骤3.2：更新线性分类器的方差，根据上述获取错误预测有标签数据，更新线性分类器的方差，公式为：

步骤4：根据更新后的线性分类器方差，在数据集中删除错误的分类器。若少数种类的样本总数不足，将会不断加入混合样例，直至总样例符合要求为止。

根据上述内容，能够获取去除错分合成的不平衡负荷数据，经过渐进学习方法逐渐平衡负荷。

3 实 验

3.1 实验模型及实验数据分析

选择了具有高度现代化水平的城市A、B，这两个城市拥有庞大的车辆和人口（大约两千万），有着良好的基础设施和电力结构，使得电动汽车得以广泛应用。

为了验证电动汽车接入配电网不平衡负荷数据渐进学习方法的可行性，在PSCAD 平台上搭建了电动汽车接入配电网的仿真模型，如图3 所示。

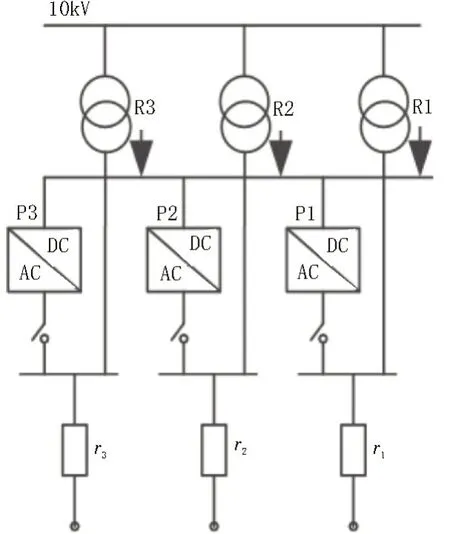
图3 电动汽车接入配电网仿真模型

由图3 可知，配电网不平衡系统直流线路额定直流电压为10 kV，R2 配电变压器对应的变流器采用电流和电压双闭环控制模式，R1 和R3 配电变压器使用功率解耦控制模式。

利用A、B 两个城市的典型日负载曲线作为初始负载曲线，分析了不同规模下的电动汽车对配电网负荷变化影响的影响，如图4 所示。

图4 不同规模下电动汽车充放电对配电网负荷变化影响

由图4 可知，第一阶段是充电时段，第二阶段是放电时段。其中城市A 的峰谷时间段是8-12 h 和20-24 h，城市B 的峰谷时间段是8-10 h、12-15 h 和20-24 h，由于不同时间点的充放电需求不同，所以两市峰谷值增加幅度也不同。

3.2 实验结果与分析

根据上述分析的实验数据，分别使用欠采样、过采样和渐进学习方法，对比分析城市A、B 不同规模下电动汽车充放电对配电网负荷变化影响，如图5所示。

由图5 可知，使用欠采样、过采样方法分析的结果与图4 所示波动曲线不一致，使用渐进学习方法分析的结果与图4 所示波动曲线一致，由此说明，使用该方法分析结果更加精准。

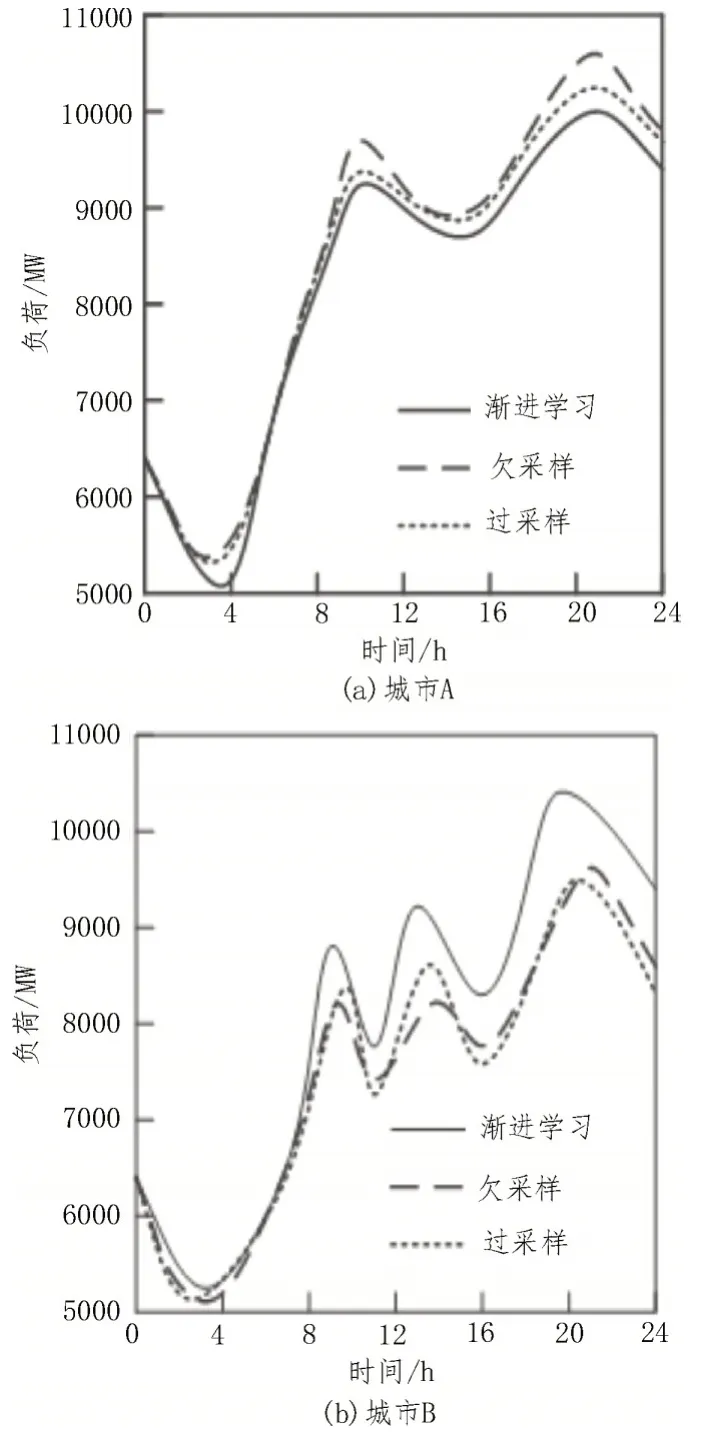
图5 三种方法电动汽车充放电对配电网负荷变化影响分析结果对比

对比三种方法不平衡数据逐渐达到平衡状态所耗费的时间，如表1 所示。

表1 三种方法耗费时间对比分析

由表1 可知，使用渐进学习方法的耗费时间最短，其与欠采样方法的最大时间差为119 ms；与过采样方法的最大时间差为61 ms。由此可知，使用所提方法能够在短时间内快速平衡负荷数据。

4 结束语

该文提出的一种电动汽车接入配电网不平衡负荷数据渐进学习方法，在线性分类器出现错误时，逐步加入综合样值，并将错误分类及时剔除。在数据达到期望的平衡状态后，利用原始数据和综合数据对学习算法进行训练，以获得最终的学习效果。实验结果表明，使用该方法能够快速平衡负荷数据。