集合与常用逻辑用语核心考点综合演练
■刘中亮(特级教师)
一、选择题
1.若非空集合A,B,U满足A∪B=U,A∩B=∅,则称(A,B)为U的一个分割,则集合U={1,2,3}的不同分割有( )。
A.5个 B.6个 C.7个 D.8个
2.下列关于集合的命题正确的个数是( )。
①很小的整数可以构成集合,②集合{y|y=2x2+1}与集合{(x,y)|y=2x2+1}是同一个集合,③这些数组成的集合有5个元素,④空集是任何集合的子集。
A.0 B.1 C.2 D.3
3.已知集合A={x|(a-1)x2+3x-2=0},若集合A有且仅有两个子集,则实数a的取值为( )。
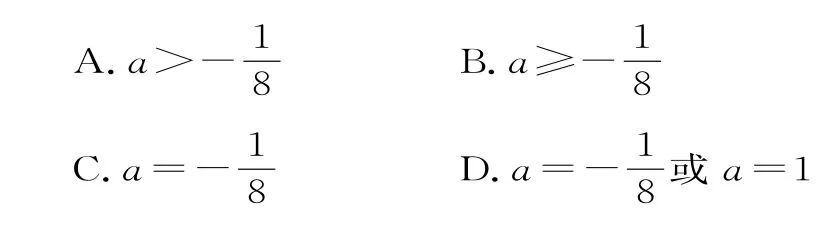
4.(多选题)以下四个命题正确的是( )。
A.“a>b”是“a2>b2”的充分条件
B.“|a|>|b|”是“a2>b2”的必要条件
C.“a>b”是“a+c>b+c”的充要条件
D.设a,b∈R,且ab≠0,若,则
5.(多选题)有以下说法,其中正确的为( )。
A.“x,y为无理数”是“xy为无理数”的充分条件
B.“x∈A∩B”是“x∈A”的必要条件
C.“x2-2x-3=0”是“x=3”的必要条件
D.“x>1”是“<1”的充分不必要条件
6.(多选题)下列命题正确的是( )。
A.“实数都大于0”的否定是“实数都小于或等于0”
B.“三角形外角和为360°”是含有全称量词的真命题
C.“至少存在一个实数x,使得|x|≥0”是含有存在量词的真命题
D.“能被3整除的整数,其各位数字之和也能被3整除”是全称量词命题
7.(多选题)下面命题正确的是( )。
A.“a>1”是“<1”的充分不必要条件
B.命题“若x<1,则x2<1”的否定是“存在x<1,则x2≥1”
C.设x,y∈R,则“x≥2 且y≥2”是“x2+y2≥4”的必要而不充分条件
D.设a,b∈R,则“a≠0”是“ab≠0”的必要不充分条件
二、填空题
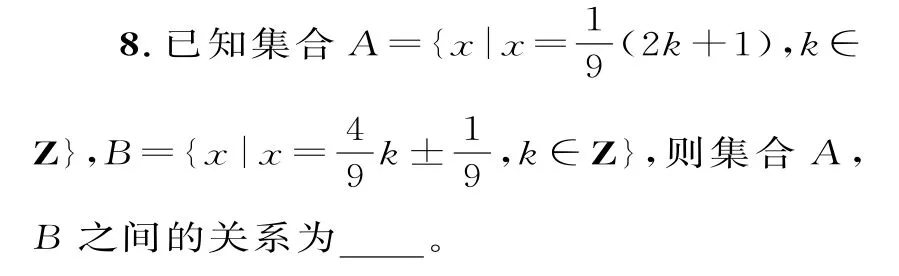
9.已知“x∈(-∞,-2)∪(0,+∞)”是“x∈[k,k+1]”的必要不充分条件,则k的取值范围是____。
10.对于任意实数a,b,c,①“a=b”是“ac=bc”的充分条件,②“a+b是无理数”是“a是无理数”的必要条件,③“a=b”是“a2=b2的充分条件,④“a>b”是“a>|b|”的必要条件。其中正确结论的序号为____。
11.已知集合A=(0,2),集合B=(-1,1),集合C={x|mx+1>0},若(A∪B)⊆C,则实数m的取值范围为____。
12.设p:-m≤x≤m(m>0),q:-1≤x≤4,若p是q的充分条件,则m的最大值为____,若p是q的必要条件,则m的最小值为_____。
三、解答题
13.已知a∈R,p:∀x∈[1 ,3],x2-a≥0,q:方程x2+2ax+2=0无实数解。
(1)若p为真命题,求实数a的取值范围。
(2)若“p∨q”为真命题,“p∧q”为假命题,求实数a的取值范围。
14.已知集合A={x|0≤x≤a},集合B={x|m2+3≤x≤m2+4},如果命题“∃m∈R,使得A∩B≠∅”为假命题,求实数a的取值范围。
15.设不等式(x-3a)(x-a-2)<0的解集为A,B={x|x<2},若x∈A是x∈B的充分不必要条件,求实数a的取值范围。
16.已知命题p:“∃x∈R,x2-2x+a=0”为假命题;命题q:“∀x∈{x|1≤x≤2},x2+ax-8≤0”为真命题,求实数a的取值范围。
17.设A为实数集,且满足条件:若a∈A,则∈A(a≠1)。
求证:(1)若2∈A,则A中必还有另外两个元素。
(2)集合A不可能是单元素集。
18.已知集合A={x|ax2-3x+2=0,x∈R,a∈R}。
(1)若A是空集,求a的取值范围。
(2)若A中只有一个元素,求a的值,并求集合A。
(3)若A中至多有一个元素,求a的取值范围。
19.设p:实数x满足x2-2ax-3a2<0(a>0),q:2≤x<4。
(1)若a=1,且p,q都为真命题,求x的取值范围。
(2)若q是p的充分不必要条件,求实数a的取值范围。
20.已知集合P={x|x2-3x+2≤0},S={x|1-m≤x≤1+m}。
(1)是否存在实数m,使x∈P是x∈S的充要条件? 若存在,求出m的取值范围,若不存在,请说明理由。
(2)是否存在实数m,使x∈P是x∈S的必要条件? 若存在,求出m的取值范围,若不存在,请说明理由。

一、选择题
1.提示:依题意可得,当集合A为{1}时,B为{2,3},当A为{2}时,B为{1,3},当A为{3}时,B为{1,2},同时对调A,B的位置,也可得到3 对集合,则符合条件的有6个。应选B。
2.提示:很小的整数可以构成集合是错误的,不满足元素的确定性,①错误。集合{y|y=2x2+1}={y|y≥1},而{(x,y)|y=2x2+1}表示的集合为函数y=2x2+1图像上的点,所以不是同一集合,②错误。1,2,这些数组成的集合有3个元素,而不是5个元素,③错误。空集是任何集合的子集,④正确。应选B。

4.提示:如2>-3⇒/22>(-3)2,A 为假命题。a2>b2⇒|a|2>|b|2⇒|a|>|b|,B为真命题。a>b⇒a+c>b+c,a+c>b+c⇒a>b,即“a>b”是“a+c>b+c”的充要条件,C为真命题。当a,b异号时,虽然<1,但是<0,D 为假命题。应选BC。
6.提示:对于A,“实数都大于0”的否定是“存在实数小于或等于0”,A 错误。对于B,“三角形外角和为360°”含有全称量词,且为真命题,B 正确。对于C,“至少存在一个实数x,使得|x|≥0”含有存在量词,且为真命题,C 正确。对于D,“能被3整除的整数,其各位数字之和也能被3 整除”是全称量词命题,D 正确。应选BCD。
7.提示:对于A,根据反比例函数的性质可知,由a>1,能推出<1,但由<1,不能推出a>1,如当a<0时,符合<1,但不符合a>1,A 正确。对于B,根据命题的否定的定义可知,命题“若x<1,则x2<1”的否定是“存在x<1,则x2≥1”,B 正确。对于C,由x≥2 且y≥2 能推出x2+y2≥4,但由x2+y2≥4不能推出x≥2 且y≥2,C 不正确。对于D,由a≠0,不能得到ab≠0,但由ab≠0,可得到a≠0,D 正确。应选ABD。
二、填空题
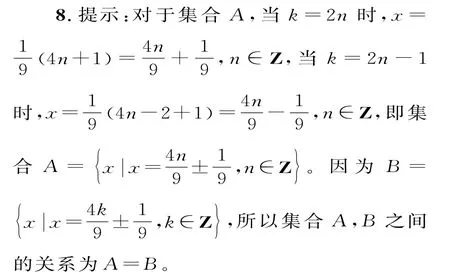
9.提示:由已知“x∈(-∞,-2)∪(0,+∞)”是“x∈[k,k+1]”的必要不充分条件,可得[k,k+1](-∞,-2)∪(0,+∞),所以k+1<-2或k>0,解得k<-3或k>0,即k的取值范围为{k|k<-3或k>0}。
10.提示:a=b⇒ac=bc,①正确。“a+b是无理数”与a是不是无理数没有关系,②错误。a=b⇒a2=b2,③正确。a>b⇐a>|b|,④正确。答案为①③④。
11.提示:由题意得A∪B=(-1,2)。

三、解答题
13.提示:(1)由命题∀x∈[1,3],x2-a≥0为真命题,可得a≤(x2)min。由x∈[1,3],可得(x2)min=1,所以a≤1。

14.提示:命题“∃m∈R,使得A∩B≠∅”为假命题,则其否定命题“∀m∈R,A∩B=∅”为真命题。当a<0时,集合A={x|0≤x≤a}=∅,符合A∩B=∅。当a≥0时,因为m2+3>0,又∀m∈R,A∩B=∅,所以a<m2+3 对于∀m∈R 恒成立,所以a<(m2+3)min=3,所以0≤a<3。综上可得,实数a∈(-∞,3)。
15.提示:不等式(x-3a)(x-a-2)<0,当3a>2+a,即a>1时,解集A={x|2+a<x<3a},若x∈A是x∈B的充分不必要条件,则AB,所以3a≤2,此时1<a≤。
当3a=2+a,即a=1时,解集A=∅,则AB,符合题意。
当3a<2+a,即a<1时,解集A={x|3a<x<2+a},若x∈A是x∈B的充分不必要条件,则AB成立,所以2+a≤2,此时a≤0。
综上可得,a的取值范围为或
16.提示:命题p:“∃x∈R,x2-2x+a=0”为假命题,可得方程x2-2x+a=0无实数解,即Δ=4-4a<0,解得a>1。
命题q:“∀x∈{x|1≤x≤2},x2+ax-8≤0”为真命题,可得解得a≤2。
综上可得,a的取值范围是{a|1<a≤2}。

(2)若A为单元素集,则,即a2-a+1=0,此方程无实数解,所以a≠,所以集合A不可能是单元素集。
18.提示:(1)若A是空集,则方程ax2-3x+2=0无解,此时a≠0,Δ=9-8a<0,所以a>。
(2)若A中只有一个元素,则方程ax2-3x+2=0有且只有一个实根。
当a=0时,方程为一元一次方程,显然满足条件;当a≠0,此时Δ=9-8a=0,解得
故a=0或若a=0,则集合;若,则集合
(3)若A中至多有一个元素,则A为空集,或有且只有一个元素。
由(1),(2)得满足条件的a的取值范围
19.提示:(1)若a=1,则x2-2ax-3a2<0 可化为x2-2x-3<0,可得-1<x<3。
若q为真命题,则2≤x<4。
所以当p,q都为真命题时,x的取值范围是
(2)由x2-2ax-3a2<0(a>0),可得-a<x<3a。
因为q:2≤x<4,q是p的充分不必要条件,所以{x|2≤x<4}{x|-a<x<3a},所以。故实数a的取值范围是
20.提示:(1)P={x|x2-3x+2≤0}={x|1≤x≤2}。
要使x∈P是x∈S的充要条件,需满足P=S,所以此方程组无解,所以不存在实数m,使x∈P是x∈S的充要条件。
(2)要使x∈P是x∈S的必要条件,则S⊆P。
当S=∅时,由1-m>1+m,解得m<0,这时满足题意;
当S≠∅时,由1-m≤1+m,解得m≥0,要使S⊆P,需满足解得m≤0,所以m=0。
综上可得,当实数m≤0时,使x∈P是x∈S的必要条件。

