思想方法引领,解题技巧应用
■崔云峰
在解数学问题中,巧妙渗透数学思想方法,借助数学思想方法的引领,不仅能培养解题能力,而且能优化认知结构,提高同学们的数学核心素养。在高一的初始阶段,通过集合知识的学习,合理借助数学思想方法,在有效提升解题技巧的同时,可以大大优化同学们的思想认知结构。
一、函数与方程思想

分析:根据集合的元素特征,借助函数与方程思想的应用,利用三个集合间参数的关系加以分析与讨论,即可判断对应集合的基本关系。


判断集合间关系的常用方法有观察法、集合元素特征法、数形结合法等。这里借助函数与方程思想加以分析,再结合集合的基本性质,使得问题圆满获解。
二、分类讨论思想
例2已知集合A={12,a2+4a,a-2},且-3∈A,则a=( )。
A.-1 B.-3或-1
C.3 D.-3
分析:根据题设条件,利用元素与集合之间的关系,构建对应的方程,结合分类讨论进行分析与判断。
解:因为集合A={12,a2+4a,a-2},且-3∈A,所以a2+4a=-3或a-2=-3,解得a=-1或a=-3。当a=-1时,a2+4a=a-2=-3,不满足集合元素的互异性,舍去;当a=-3时,A={12,-3,-5},符合题意。
综上可知,a=-3。应选D。

在解决此类集合问题时,要注意集合元素的基本性质,特别是元素的互异性。分类讨论思想主要应用于含参数的集合问题,同学们要加以重视。
三、数形结合思想
例3学校举办秋季运动会时,高一(2)班共有24 名同学参加比赛,有12 人参加游泳比赛,有9人参加田赛,有13人参加径赛,同时参加游泳比赛和田赛的有3 人,同时参加游泳比赛和径赛的有3 人,没有人同时参加三项比赛。那么同时参加田赛和径赛的有____人。
分析:根据题设条件,设出对应的参数并作出Venn图,借助数形结合法,合理构建对应的方程组求解。
解:设同时参加田赛和径赛的有x人,只参加田赛的有y人,只参加径赛的有z人,画出Venn图,如图1所示。
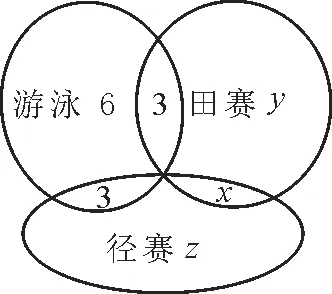
图1

集合中常用的数形结合法有数轴法和Venn 图法。借助数轴或Venn 图,将抽象的数学语言与直观的图形结合起来,使抽象思维与形象思维结合,通过对图形的认识、数形结合的转化,可以培养思维的灵活性、形象性,实现所求问题的化难为易、化抽象为具体。
四、极限思想
例4不等式组的解集是( )。

分析:直接求解涉及含有绝对值的分式不等式,比较烦琐,而借助极限思想,由方程根的验证,回归到相应的不等式问题,从而达到合理转化的目的。

极限思想是创新思维中的一个重要数学思想,在解决一些客观题时,巧妙借助极限思想,可以实现从抽象到具体、从无限到有限、从近似到精确等方面的跨越。
五、创新思想
例5(多选题)设集合P为实数集R 的非空子集,若对任意x,y∈P,都有x+y,x-y,xy∈P,则称集合P具有“封闭性”。下列说法中正确的是( )。
B.若集合P具有“封闭性”,则一定有0∈P
C.具有“封闭性”的集合一定是无限集
D.若集合P具有“封闭性”,则满足P⊆T⊆R 的任意集合T也具有“封闭性”
分析:根据新定义的“封闭性”,结合选项加以分析,利用不同的视角切入求解。


解决集合中的新定义问题,关键是挖掘新定义的本质,借助逻辑推理、代数运算,有时也可以通过特殊值法处理或举反例等方式求解。此题以多选题的形式出现,设置不同的情境,借助不同方法来分析与处理,更好地渗透了数学思想,倡导创新意识与创新应用。

1.已知a为实数,使“∀x∈[3 ,4],xa<0”为真命题的一个充分不必要条件是____。
提示:全称量词命题:∀x∈[3,4],xa<0为真命题,所以a>x在区间[3,4]上恒成立,所以a>4,所以使“∀x∈[3,4],xa<0”为真命题的一个充分不必要条件是(4,+∞)的真子集,则a>5满足条件(本题答案不唯一)。
2.对于任意的实数x,不等式|x+1|≥kx恒成立,则实数k的取值范围是_____。
提示:不等式|x+1|≥kx恒成立,则y=|x+1|的图像不能在y=kx的图像的下方(图略),结合图像得0≤k≤1。

