集合与常用逻辑用语常见典型考题赏析

■姚 平

集合是高中数学的重要内容,也是高考的必考内容,高考主要考查集合的概念与性质,集合间的关系与运算,集合与其他知识的综合应用。常用逻辑用语是重要的数学概念,对于这部分内容,高考主要以填空题的形式出现,考查四种命题的关系、命题的否定,以及命题真假的判断等。

题型一：集合的基本概念

用描述法表示集合,首先要搞清楚集合中代表元素的含义,再看元素的限制条件,明白集合的类型,是数集、点集还是其他类型的集合。集合中元素的互异性常常容易忽略,特别是含有字母的集合,在求出字母的值后,要注意检验集合中元素是否满足互异性。分类讨论的思想方法常用于解决集合问题。

例1选择适当的方法表示下列集合:①大于1且小于8的有理数;②由(a,b∈R)所确定的实数集合;③不等式2x-3＜5的解组成的集合。

解：①大于1 且小于8 的有理数有无数个,用描述法表示为{x∈Q|1＜x＜8}。②根据绝对值的意义化简求解,设当a＞0,b＞0 时,x=2;当a＜0,b＜0 时,x=-2;当a,b异号时,x=0。故用列举法表示为{-2,0,2}。③不等式2x-3＜5的解组成的集合可用描述法表示为{x|2x-3＜5},即{x|x＜4}。

跟踪训练1：用描述法表示下列集合:①被3除余1 的正整数的集合;②坐标平面内第一象限的点的集合;③大于4的所有偶数。

提示：①被3 除余1 的正整数的集合可表示为{x|x=3n+1,n∈N}。②由于第一象限内的点的横、纵坐标均大于零,故此集合可表示为{(x,y)|x＞0,y＞0}。③偶数可表示为2n,n∈Z,又大于4,则n≥3,用描述法表示此集合为{x|x=2n,n∈Z且n≥3}。

题型二：集合之间的基本关系

空集是任何集合的子集,在涉及集合关系时,必须优先考虑空集的情况,否则会造成漏解。已知两个集合间的关系求参数时,关键是将条件转化为元素或区间端点间的关系,进而转化为参数所满足的关系。常用数轴、Venn图来直观解决这类问题。

例2设集合A={0,1,2},B={m|m=x+y,x∈A,y∈A},则集合A与B的关系为( )。

A.A∈BB.A=B

C.B⊆AD.A⊆B

解：因为集合A={0,1,2},B={m|m=x+y,x∈A,y∈A}={0,1,2,3,4},所以A⊆B。应选D。

跟踪训练2：已知集合A={-1,3,2m-1},B={3,m2}。若B⊆A,则实数m等于( )。

A.±1 B.-1

C.1 D.0

提示：已知集合A={-1,3,2m-1},集合B={3,m2}。

若B⊆A,则m2∈A,且m2≠3。因为m2≥0,所以m2=-1无解,所以m2=2m-1,解得m=1,经检验符合元素的互异性。应选C。

题型三：集合的运算

集合是由元素组成的,从研究集合中元素的构成入手是解决集合运算问题的前提。有些集合是可以化简的,先化简再研究其关系并进行运算,可使问题简单明了,易于解决。注意数形结合思想的应用,可用数轴、坐标系或Venn图帮助求解。

例3已知集合,集合N={x|x≤-3},则集合{x|x≥1}=( )。

A.M∩NB.M∪N

C.∁R(M∩N) D.∁R(M∪N)

解：由,解得-3＜x＜1,所以M∪N=(-∞,1)。应选D。

跟踪训练3：已知全集U={-1,0,1,2,3,4},集合A={x|x≤1,x∈N},B={1,3},则∁U(A∪B)=( )。

A.{4} B.{2,4}

C.{-1,2,4} D.{-1,0,2,4}

提示：因为A={x|x≤1,x∈N}={0,1},B={1,3},所以A∪B={0,1,3},所以∁U（A∪B）={-1,2,4}。应选C。

题型四：利用集合的运算求参数

根据集合运算求参数,先把符号语言译成文字语言,然后应用数形结合法求解。涉及子集问题,要分该集合是空集、不是空集两种情况求解。

例4已知集合A={x|3x2-2x-1≤0},B={x|2a＜x＜a+3},若A∩B=∅,则实数a的取值范围是( )。

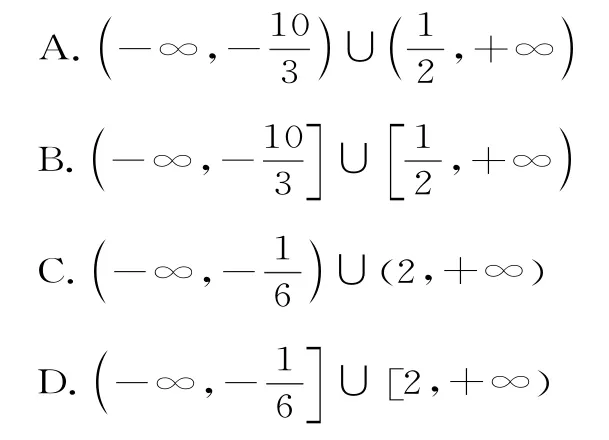
跟踪训练4：设全集U=R,已知集合A={x|x＜3或x≥9},B={x|x≥a}。若(∁UA)∩B≠∅,则a的取值范围为( )。

A.a＞3 B.a≤3

C.a＜9 D.a≤9

提示：因为A={x|x＜3或x≥9},所以∁UA={x|3≤x＜9}。若(∁UA)∩B≠∅,则a＜9。应选C。

题型五：已知集合关系求参数

涉及与子集有关的参数问题,要注意检验是否出现集合相等的情况,同时要注意端点是否取等号的情况。

例5(1)已知集合A={1+x2,x},B={1,2,3},且A⊆B,则 实 数x的 值是( )。

A.-1 B.1

C.3 D.4

(2)若集合A={x∈R||x-4|≤2},集合B={x∈R|2a≤x≤a+3},若B⊆A,则实数a的取值范围是( )。

A.{a|a＞3}

B.{a|a≥1}

C.{a|1＜a＜3}

D.{a|1≤a≤3}

解：(1)由A⊆B,可知1+x2∈B且x∈B,逐个代入检验知x=1 符合题意,所以x=1。应选B。

(2)集合A={x∈R||x-4|≤2}=[2,6]。若集合B为空集,则2a＞a+3,即当a＞3时满足题意;

若B不为空集,则2a≤a+3,即a≤3,由B⊆A得解得a∈[1,3]。

综上可知,a∈[1,+∞)。应选B。

跟踪训练5：已知集合A={2,-1},集合B={m2-m,-1}。若A=B,则实数m等于( )。

A.2 B.-1

C.2或-1 D.4

提示：因为A=B,所以m2-m=2,解得m=2或m=-1。应选C。

题型六：定义法判断充要条件

确定谁是条件,谁是结论;尝试从条件推结论,若条件能推出结论,则条件是结论的充分条件,否则条件就不是结论的充分条件;尝试从结论推条件,若结论能推出条件,则条件是结论的必要条件,否则条件就不是结论的必要条件。提醒:不能将“若p,则q”与“p⇒q”混为一谈,只有“若p,则q”为真命题,才有“p⇒q”。

例6设集合A={1,a},B={1,2,3},则“a=3”是“B⊇A”的( )。

A.充分条件

B.必要条件

C.既不充分也不必要条件

D.既充分又必要条件

解：当a=3时,集合A={1,3},B={1,2,3},所以B⊇A正确,即“a=3”是“B⊇A”的充分条件。应选A。

跟踪训练6：若集合A={x|x＞0},则下列不等式是“a∈A”的充分不必要条件的是( )。

A.a＞-1 B.a＞1

C.a≥0 D.a＞0

提示：集合A={x|x＞0},当a＞1 时,a∈A,反之不成立,即为充分不必要条件。应选B。

题型七：充分性、必要性的证明

证明充要条件一般分为两个步骤,即证明充分性和必要性这两个方面。充分性就是要证明条件⇒结论,必要性就是要证明结论⇒条件。在证明之前,一定要先分清楚哪个是条件,哪个是结论。

例7已知x,y都是非零实数,且x＞y,求证的充要条件是xy＞0。

跟踪训练7：求证:一元二次方程ax2+bx+c=0 有一正根和一负根的充要条件是ac＜0。

提示：(必要性)因为方程ax2+bx+c=0有一正根和一负根,所以Δ=b2-4ac＞0且x1x2=＜0(x1,x2为方程的两根),所以ac＜0。

(充分性)由ac＜0,可得Δ=b2-4ac＞0及x1x2=＜0(x1,x2为方程的两根),所以方程ax2+bx+c=0有两个相异实根,且两根异号,即方程ax2+bx+c=0有一正根和一负根。

综上所述,一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac＜0。

题型八：利用充分条件、必要条件求参数的取值范围

利用充分、必要、充要条件求参数范围的解法步骤:化简p,q两命题;根据p与q的关系(充分、必要、充要条件)转化为集合间的关系;利用集合间的关系建立不等式;求参数的取值范围。

例8已知p:|x+1|＞2,q:x＞a,且¬p是¬q的充分不必要条件,则a的取值范围是( )。

A.a≤1 B.a≤-3

C.a≥-1 D.a≥1

解：已知p:|x+1|＞2,可化为p:x＜-3或x＞1。

由题意可知,q中变量取值的集合是p中变量取值集合的真子集,所以a≥1。应选D。

跟踪训练8：已知p≥1,q:|x-a|＜2,若p是q的充分不必要条件,则实数a的取值范围为( )。

A.(-∞,4] B.[1,4]

C.(1,4] D.(1,4)

提示：由,可得,解得2＜x≤3。由|x-a|＜2,可得a-2＜x＜a+2。

由p是q的充分不必要条件,可得解得1＜a≤4。故实数a的取值范围为(1,4]。应选C。

题型九：全称、特称命题求参数

对于全称命题“∀x∈M,a＞f(x)(或a＜f(x))”为真的问题,实质就是不等式恒成立问题,通常转化为求函数f(x)的最大值(或最小值),即a＞f(x)max(或a＜f(x)min)。对于特称命题“∃x0∈M,a＞f(x0)(或a＜f(x0))”为真的问题,实质就是不等式能成立问题,通常转化为求函数f(x)的最小值(或最大值),即a＞f(x)min(或a＜f(x)max)。

A.(1,+∞) B.(-∞,2]

C.(1,2) D.(-1,2]

跟踪训练9：命题“已知y=x-1,∀x∈R 都有m≤y”是真命题,则实数m的取值范围是( )。

A.m≥-1 B.m＞-1

C.m≤-1 D.m＜-1

提示：由已知y=|x|-1,可得y≥-1。要使∀x∈R,都有m≤y成立,只需m≤-1。应选C。

题型十：特称命题的判断

要判断一个存在量词命题是真命题,只要在限定集合M中,找到一个x,使p(x)成立即可;否则,这一存在量词命题就是假命题。要判断一个全称量词命题是真命题,需证明∀x∈D,p(x)都成立。

例10指出下列命题是全称量词命题还是存在量词命题,并判断它们的真假。

(1)∀x∈N,2x+1是奇数。

(2)存在一个x∈R,使

(3)对任意实数a,|a|＞0。

解：(1)是全称量词命题。因为∀x∈N,2x+1都是奇数,所以该命题是真命题。

(2)是存在量词命题。因为不存在x∈R,使成立,所以该命题是假命题。(3)是全称量词命题。因为,所以|a|＞0不都成立,所以该命题是假命题。

跟踪训练10：现有下列命题:①有些自然数是偶数;②正方形是菱形;③能被6整除的数也能被3整除;④对于任意x∈R,总有。则所有存在量词命题的个数是( )。

A.0 B.1 C.2 D.3

提示：命题①中含有存在量词,是存在量词命题。命题②中全称量词省略,可以叙述为“所有的正方形都是菱形”,是全称量词命题。命题③中全称量词省略,可以叙述为“一切能被6整除的数也都能被3整除”,是全称量词命题。命题④中有全称量词“总有”,是全称量词命题。应选B。

判断下列命题是全称量词命题还是存在量词命题,然后写出对应的否定命题,并判断真假。

①不论m取何实数,关于x的方程x2+x-m=0必有实数根。②所有末位数字是0或5的整数都能被5整除。③某些梯形的对角线互相平分。④函数y=kx的图像恒过原点。

提示:①是全称量词命题。其否定为“存在实数m,使得方程x2+x-m=0没有实数解”,是真命题。②是全称量词命题。其否定为“存在末位数字是0 或5 的整数不能被5整除”,是假命题。③是存在量词命题。其否定为“所有梯形的对角线不互相平分”,是真命题。④是全称量词命题。其否定为“存在实数k,使函数y=kx的图像不过原点”,是假命题。