青藏高原地区纤维混凝土抗冻耐久性试验与损伤模型研究

邓祥辉,张 鹏,王 睿,吴起源,王 旭

(1.西安工业大学建筑工程学院,西安 710021;2.西安市军民两用土木工程测试技术与毁损分析重点实验室,西安 710021;3.中国五冶集团有限公司,成都 610063)

0 引 言

在我国青藏高原地区,受季风和地理环境的影响,气候具有干燥、高寒、昼夜温差大的特点。在高原高寒极端环境条件下,民用建筑、高速公路、铁路工程等基础设施由于冻融损伤,其承载能力会降低,耐久性会下降,结构安全受到威胁。因此,提高混凝土结构的耐久性[1-2],尤其是抗冻耐久性[3-4],成为青藏高原地区基础设施研究的一个重点和难点问题。

截至目前,国内外学者对混凝土抗冻耐久性进行了大量研究,并取得很多成果。如李金玉等[5]对三种类型混凝土(普通、引气和高强)进行冻融损伤试验,并结合扫描电子显微镜和X射线衍射分析来探索冻融过程中的破坏机理,提出混凝土微孔结构的增加会促使混凝土的宏观强度和密实度等性能降低。邓祥辉等[6]对引气再生混凝土进行冻融试验和物理力学性能测试,并结合核磁共振试验结果,提出引气再生混凝土的抗冻耐久性与其试件内部中、小孔隙占比密切相关。Rustamov等[7]对钢纤维和聚乙烯醇纤维在冻融循环作用下混凝土力学性能影响进行研究,结果表明混掺纤维混凝土比无纤维混凝土具有更强的抗开裂和冻融损伤能力。随着对纤维混凝土抗冻耐久性研究的深入,一些学者对纤维混凝土抗冻耐久性损伤模型进行了深入研究。如程红强等[8]基于快速冻融试验,并结合纤维混凝土冻融损伤机理,推导出聚丙烯纤维混凝土在冻融循环下的强度损伤模型。刘崇熙等[9]针对水工混凝土大坝的耐久性问题,对四种不同水灰比的引气混凝土分别进行快速冻融循环试验,总结试验结果得到相对动弹性模量和冻融循环次数之间的关系,并以此对大坝混凝土的理想寿命进行了预测。乔宏霞等[10]分析了不同纤维掺加方式混凝土力学性能与冻融损伤次数的衰减规律,并建立了不同纤维掺加方式成型混凝土的强度损失演变模型。赵小明等[11]对不同纤维和粉煤灰掺量的混凝土进行了冻融试验,并结合试验测定的纤维混凝土耐久性指标和抗压强度,以动弹性模量建立了二次函数衰减模型,该模型拟合精度较高且能反映纤维混凝土的冻融损伤程度。

在高海拔地区,混凝土和混凝土结构性冻融损伤机理和演化过程更为复杂,目前这方面的研究工作比较缺乏。而在相关研究领域,如在高海拔地区提高混凝土耐久性方面的配合比优化、外加剂掺加、耐久性评价方面取得了一些成果。如周志东等[12]通过研究高海拔地区混凝土耐久性,提出相关措施,如加强高原新型混凝土(原材料、优化配合比等)方面的研究。米永刚等[13]针对高寒地区混凝土耐久性不足的问题,制备了C65高性能混凝土,并提出动弹性模量可以作为耐久性评估的主要耐久性评价指标。刘旭等[14]对低气压环境下水泥混凝土性能的研究现状进行了总结,认为低气压养护会对混凝土力学与收缩性能产生不利影响。李雪峰等[15]将地表温度近似代替混凝土表面温度,对青藏高原大部分地区混凝土年均冻融循环次数进行估算,分析得出高原地区应加强对混凝土抗冻耐久性设计。Ge等[16-17]通过环境模拟系统来模拟高原地区的恶劣环境,结果表明低气压会降低混凝土的抗压强度和耐久性。从上述分析可以看出,现有的关于纤维混凝土抗冻耐久性试验的研究基本上是在一般地区的实验室进行,主要是通过对不同纤维种类、掺量、外加剂和不同混凝土类型进行冻融循环试验,在试验结果分析基础上建立相应的冻融损伤模型。几乎没有人在高海拔地区依托建设工程项目进行现场试验,研究高原气候对纤维混凝土抗冻耐久性的影响及其冻融损伤模型。

综合现有研究可见,在一般地区对纤维混凝土抗冻耐久性的研究较多,但在青藏高原地区通过现场试验研究纤维混凝土抗冻耐久性方面相对缺乏,尤其是高原地区混凝土抗冻损伤机理及损伤模型方面的研究几乎没有。青藏高原气候条件复杂,低气压对混凝土内部结构影响较大,海拔增高,气压变低,水的沸点变低,混凝土硬化时水化热变小,导致水化不完全,强度达不到预期。加之青藏高原地区温度低、温差大、日照强等特点严重影响混凝土的耐久性,因此,在这种情况下进行现场混凝土物理力学试验和理论模型分析就显得尤为重要。基于以上问题,拟通过掺加不同外加剂(冲磨剂、膨胀剂)方式下,探究青藏高原地区纤维混凝土在冻融循环过程中的物理力学性能以及混凝土结构冻融损伤机理。并在此基础上,考虑青藏高原地区环境特点,提出高原低气压环境下的损伤模型和抗折强度预测方程。

1 实 验

本研究依托西藏那曲某混凝土道路工程,该工程海拔约为4 500 m,大气压力约为56 kPa(标准大气压力为101.325 kPa)。工程所在地属亚寒带气候区,干燥且多大风,项目所在地年平均气温-1.9 ℃,年降水量10～20 cm,年日照天数237～240 d,全年无绝对无霜期。

1.1 试验材料及配合比

本试验采用工程所用原材料,具体为:水泥为P·O 52.5级水泥,细骨料为天然河沙,粗骨料4.75～31.5 mm的矿山碎石且级配良好,水为当地自来水,纤维为聚酯纤维。外加剂采用江苏苏博特新材料股份有限公司生产的引气剂、减水剂。膨胀剂为HME®-Ⅳ混凝土高效膨胀剂,常用掺量为水泥总量的6%～10%(等质量取代水泥)。抗冲磨剂为SBT®-KCM(Ⅰ)抗冲磨剂,常用掺量为2%～5%(等质量取代水泥)。

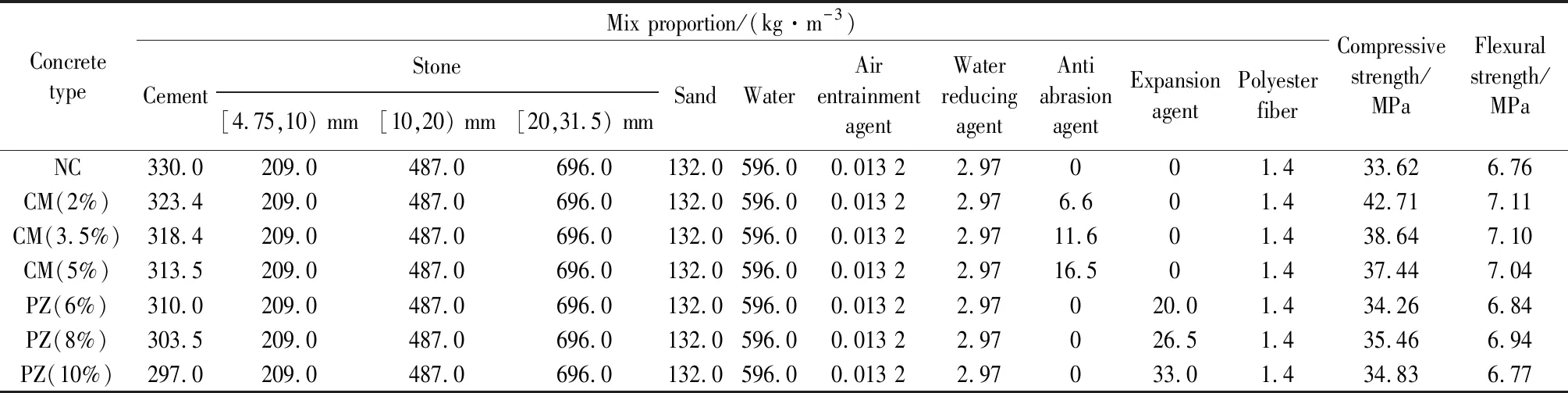
表1 纤维混凝土配合比及强度

从表1可见,与膨胀纤维混凝土组中的PZ(8%)的力学性能相比,PZ(6%)的抗压、抗折强度分别小1.20、0.10 MPa,PZ(10%)的抗压、抗折强度分别小0.63、0.17 MPa。因此,膨胀纤维混凝土中掺量为8%的相对较好。与冲磨纤维混凝土组中的CM(2%)的力学性能相比,CM(3.5%)的抗压、抗折强度分别小4.07、0.01 MPa,CM(5%)的抗压、抗折强度分别小5.27、0.07 MPa。因此,冲磨纤维混凝土中掺量为2%的相对较好。基于上述试验结果,选取掺量为8%的PZ和掺量为2%的CM进行后续的冻融试验。

1.2 试件制备及编号

冻融试验试块为棱柱体100 mm×100 mm×400 mm,基于力学试验结果,制备对照组NC、CM(2%)、PZ(8%)三种配合比的纤维混凝土试件。冻融循环试验中,CM(2%)记做CM,PZ(2%)记做PZ,每种纤维混凝土39块,分为13组(每组3块),进行抗冻耐久性试验。以NC为例,第1组编号为NC1～3,第2组为NC4～6,第13组为NC36～39,其中NC1～3为0次冻融循环时进行测试的试件,NC4～6为25次冻融循环时进行测试的试件,NC7～9为50次冻融循环时进行测试的试件,以此类推直至300次冻融循环。CM、PZ纤维混凝土的试件编号同理。

1.3 试验内容与测试方法

根据力学试验结果,本文选取NC、CM(2%)、PZ(8%)开展冻融损伤试验,根据《普通混凝土长期性能和耐久性能试验方法标准》(GB/T 50082—2009)[18],单次试验冻融循环周期2～4 h,试件中心温控范围在-20～7 ℃。本试验设置一次冻融循环时间为3.2～4 h,试件中心温度最高为5 ℃和最低为-17 ℃。将24 d的试件放在(20±2) ℃的水中浸泡4 d,对冻融0次的试块直接测定初始(质量、动弹性模量、超声波、抗折强度)并记录,其余试块在TDR-3冻融箱中进行冻融试验,每冻融循环25次,取出3个待测定平行试块,并用干燥的棉布擦拭试件表层水分后,对质量、动弹性模量、超声波、抗折强度进行测定,直至到达相对性弹性模量的60%或质量损失率5%,终止试验。

2 结果与讨论

2.1 表观现象分析

表观观察可以直接反映冻融循环对混凝土表层的影响。本试验在每经过25次冻融循环后,从冻融箱取出试件,擦干表层进行观察和测试。第一阶段(Ⅰ),冻融循环0次时,NC试件棱角完好,表层较平滑。与NC相比,CM表层更加平滑,而PZ试件表层有粗糙且小孔洞。第二阶段(Ⅱ),冻融循环150次时,NC试件棱角出现残缺,表层起皮,砂浆轻微剥落。与NC相比,CM试件棱角完整、部分表层起皮,而PZ试件棱角有小块掉落,表层小孔洞增多,砂浆剥落明显。第三阶段(Ⅲ),冻融循环终止时,NC试件外层砂浆剥落部分较多,骨料清晰可见,试件出现小部分残缺。与NC相比,CM试件表面的水泥砂浆剥落很少,试件保持较好的完整性,PZ试件表面剥落、掉渣严重,且大碎石(20～31.5 mm)暴露明显。三种纤维混凝土试件试验时情况如图1～图3所示。

图1 冻融循环作用下NC的表层形态变化

图2 冻融循环作用下CM的表层形态变化

图3 冻融循环作用下PZ表层形态变化

三种混凝土试件在冻融损伤过程中表现出很大差异,与其他两种混凝土相比,CM在经历冻融循环后才出现表层砂砾和水泥浆体轻度剥落,棱角只有小部分残缺,无大粒径骨料外露情况。因此,从本次试验看,掺入适量的抗冲磨剂可以改善纤维混凝土抗冻耐久性。这种改善的主要原因是抗冲磨剂可以有效提高纤维混凝土的密实性,减少内部损伤与缺陷,使试件具有较好的完整性,从而改善纤维混凝土的抗冻耐久性。

2.2 冻融过程中质量损失和动弹性模量损失分析

混凝土试块质量损失的测定反映了试块表面的损伤,而动弹性模量的测定间接反映了混凝土内部缺陷程度状况,两者都是现行混凝土规范中评估混凝土抗冻耐久性的指标。本试验对最优力学性能的三种纤维混凝土试件进行了冻融试验,根据试验测定结果绘制了试验中纤维混凝土的质量损失率和动弹性模量的变化曲线,如图4和图5所示。在本次试验过程中,50次冻融循环之前,三种纤维混凝土的质量损失率呈先减后增的趋势,动弹性模量呈先增后减的趋势,原因是在冻融初期,混凝土的孔隙在冻胀力的作用下变大,混凝土质量吸水增加。50次冻融循环后,动弹性模量和质量变化趋势总体上呈逐渐降低的趋势。其中,动弹性模量近似抛物线的衰减趋势,且曲率越小,衰减越平稳。

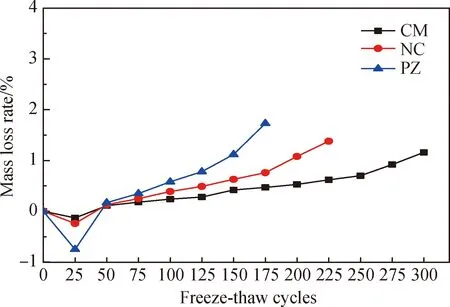
图4 冻融循环下的纤维混凝土质量损失率变化曲线

图5 冻融循环下的纤维混凝土动弹性模量变化曲线

从图5可见,在冻融循环0次时,NC的动弹性模量最小,CM的动弹性模量最大,PZ的动弹性模量介于中间。冻融循环试验初期,三种纤维混凝土的动弹性模量均出现了上升的现象。具体为:冻融循环25次时,三种纤维混凝土动弹性模量分别上升0.96%、0.61%、3.70%;随着冻融循环试验进行,PZ在冻融循环25次后,动弹性模量开始迅速下降;而NC和CM分别经历125次和200次冻融循环后,动弹性模量开始加速下降。其中,PZ经历175次冻融循环后,相对动弹性模量快速降到49.77%,到达试验终止条件;NC经历225次冻融循环后,相对动弹性模量快速降到56.70%,到达试验终止条件;CM经历300次冻融循环后,相对动弹性模量快速降到49.18%,到达冻融试验终止条件。

总体来说美国倦怠科室稳中有变，重症医学和急诊医学倦怠高发，家庭医学最近两年都有上榜。重症医学和急诊医学的倦怠发生比率一直都很高，这似乎不意外，但是家庭医学医生在近三年都表现了比较高的倦怠(2016年排名第4，2017年排名第3，2018年排名第3)。我国为了解决基本医疗资源不足的问题，从2011年起开始在全国推行家庭医生制度，家庭医生群体会逐渐扩大，一般认为家庭医生服务较基础，患者需求较简单，但从美国经验看，仍然需要关注这个群体的任务量，预防可能的职业倦怠。

2.3 冻融过程中超声波损失分析

超声波波速可以检测材料内部结构的变化情况。冻融循环会引起混凝土内部结构的疲劳损伤,进而也会导致超声波波速的变化。因此,通过超声波波速的变化可以评价混凝土内部的密实度情况。冻融试验后,三种纤维混凝土的超声波波速曲线如图6所示。

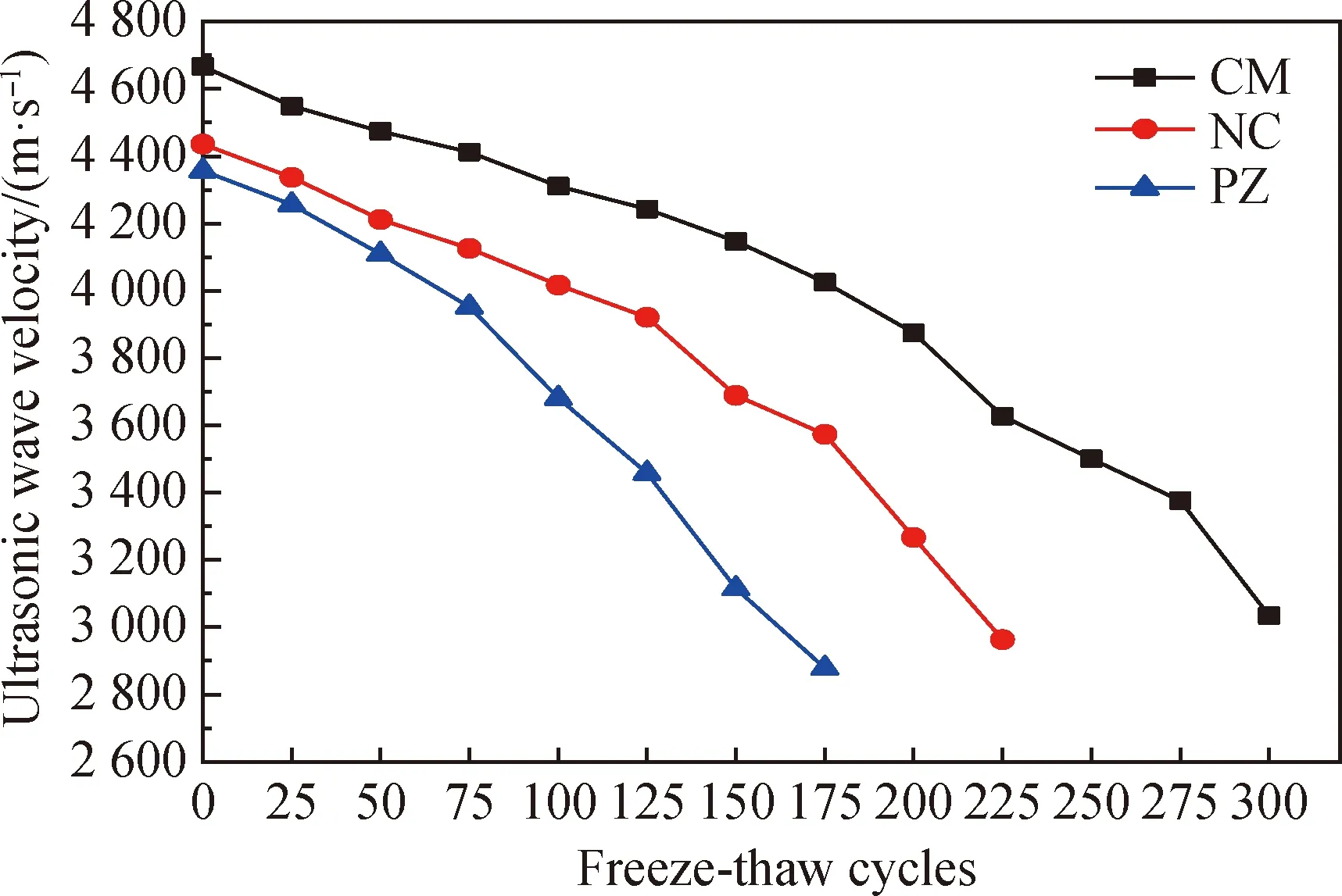
图6 冻融循环下纤维混凝土超声波波速变化曲线

从图6可以看出,在冻融循环0次时,CM的超声波波速为4 667 m/s,而NC和PZ的超声波波速分别为4 436和4 357 m/s,两者接近。由此可见,掺入抗冲磨剂可有效改善混凝土的密实度,而掺入膨胀剂会降低混凝土的密实度。NC的超声波波速在历经125次冻融循环后快速下降,PZ的超声波波速在历经25次冻融循环后快速下降,CM的超声波波速在历经200次冻融循环后快速下降。此外,当冻融循环到达破坏条件时,三种纤维混凝土(CM、NC、PZ)的超声波波速与初始值对比分别下降到65.01%、66.79%和66.06%。这一趋势与质量损失和动弹性模量的变化趋势相近。

2.4 冻融过程后抗折强度变化分析

通常情况下,混凝土结构在冻融过程中其强度会随着冻融次数的增加而降低。因此,强度损失率也是评价混凝土冻融损伤的程度一个重要指标。根据本次试验的特点,对冻融试验后的棱柱体(尺寸为:100 mm×100 mm×400 mm)试件进行抗折强度测试,抗折强度试验结果如图7所示。

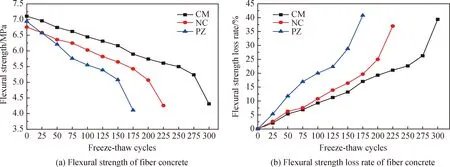
图7 冻融循环下纤维混凝土的抗折强度及强度损失率

从图7可以看出,冻融循环0次时,纤维混凝土(NC、CM、PZ)的抗折强度分别是6.76、7.11和6.94 MPa。相比较而言,初始状态时CM的抗折强度高一点。在0～75次冻融循环时,三种混凝土抗折强度损失率曲线近似直线。随着冻融次数的增加,三种混凝土抗折强度下降情况明显不同。与冻融循环0次相比,PZ在冻融循环175次时的抗折强度下降到4.11 MPa,抗折强度损失率为40.78%;NC在冻融循环225次时的抗折强度下降到4.26 MPa,抗折强度损失率为36.98%;而CM在冻融循环300次时的抗折强度下降到4.31 MPa,抗折强度损失率为39.38%。此外,在冻融循环终止时,与冻融循环0次的抗折强度相比,CM的抗折强度损失率减少了39.38%,经历了冻融循环300次。从这个试验结果可以看出,CM耐久性最好,PZ冻融前的抗折强度较高,而冻融耐久性最差。因此,掺加膨胀剂对提升纤维混凝土的抗冻作用不明显。CM冻融前的抗折强度最高,且冻融耐久性最好,出现这种情况的原因是掺加抗冲磨剂可以改善混凝土材料级配,使混凝土内部颗粒形成紧密堆积。同时,抗冲磨剂的掺加对水泥浆体有吸附分散以及润滑作用,显著提高混凝土的密实性和均质性,改善混凝土内部孔隙结构分布,从而减小混凝土在冻融过程中的抗折强度损失率。

3 高原低气压纤维混凝土损伤模型

3.1 动弹性模量损伤模型

混凝土的冻融损伤是正负温差反复作用累积的过程,损伤累积导致其内部结构从密实变得疏松,进而影响耐久性。冻融循环试验可以反映混凝土冻融环境下的损伤变化,评价混凝土冻融损伤程度和抗冻性能。同时,混凝土结构寿命与冻融损伤程度密切相关,建立理论模型能够方便预测冻融损伤,进而保证混凝土结构的寿命。然而,一般地区与高原地区海拔显著不同,不同海拔地区建议的损伤模型都有自身适应性,因此建立高原地区混凝土冻融损伤模型是非常必要的。高原低气压环境下,含气量的多少与大气压强密切相关[19-22]。通常情况下,大气压强会随海拔高度的增加而逐渐递减。在高原地区,大气压强的降低会直接影响混凝土内部的含气量,进而影响混凝土的强度和抗冻耐久性[23-24]。为了体现高原气压对混凝土抗冻耐久性的影响,本文引入气压影响系数α(α为P/P0)。由混凝土损伤力学原理,定义混凝土冻融损伤变量,假设冻融循环后的纤维混凝土动弹性模量函数为可微分函数E(N),E0为0次冻融时纤维混凝土动弹性模量,EN为第N次冻融循环的混凝土动弹性模量,EN与E0的比值为相对动弹性模量,记作Er,纤维混凝土冻融循环N次到N+ΔN次的动弹性模量衰减率如式(1)～(3)所示。

(1)

E(N+ΔN)-E(N)=-αβE(N)ΔN

(2)

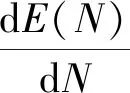
(3)

对式(3)积分得

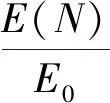
(4)

建立纤维混凝土动弹性模量模型D(N):

(5)

Er=e-αβN

(6)

式中:E(N+ΔN)为冻融循环N+ΔN次时纤维混凝土动弹性模量,MPa;E(N)为冻融循环N次时纤维混凝土动弹性模量,MPa;Δ(N)为纤维混凝土冻融循环次数增加数,P为所在地的大气压强,kPa,与海拔高度有关;β为所在地区相对大气压下的单位冻融循环次数内的动弹性模量损失率且为大于0的常数;α为气压影响系数,相关取值见表2。对表2数据分析,不同海拔高度h下,采用非线性插值法确定气压影响系数的参考值。

表2 气压影响系数α的取值

3.2 基于动弹模损伤模型的抗折强度预测方程

如图7所示,随着冻融次数的增加,三种纤维混凝土(CM、PZ、NC)的抗折强度损失率随之变大,且冻融后的强度损失率与冻融次数正相关,单位冻融循环次数内抗折强度损失率为常数。假设冻融N次循环后纤维混凝土抗折强度函数为F(N),且可微分,冻融前的抗折强度为F0,η为冻融后的单位强度损失率且大于0,则纤维混凝土冻融循环N次到N+ΔN次的抗折衰减率如式(7)～(9)所示。

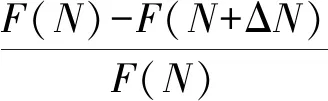
(7)

F(N+ΔN)-F(N)=-ηF(N)ΔN

(8)

(9)

对式(9)积分得

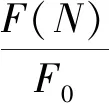
(10)

对式(6)恒等变形得

(11)

联立式(10)、(11)并化简得

(12)

式中:η/β为常数,记作c。对NC、CM、PZ三种纤维混凝土的冻融后相对抗折强度与相对动弹性模量进行回归分析(见图8),得到两者的关系,如式(13)所示。

图8 相对动弹性模量与相对抗折强度拟合关系图

(13)

根据上述推导,建立如式(14)所示的纤维混凝土抗折强度预测方程。

(14)

对NC的抗折强度准确性分析,将冻融循环0～225次的相对动弹性模量数据代入式(14),得到表3,从预测结果看,NC的抗折强度预测值与实际试验值的变化趋势基本一致。随着冻融试验的进行,抗折强度试验值与预测值误差最大出现在第125次冻融循环,误差率为6.20%;抗折强度试验值与预测值误差最小出现在第225次冻融循环,误差率为0.97%。由图9(a)NC试验值与预测值的抗折强度变化可知,25、50、75、100、125、150、225次冻融下的抗折强度预测值略微偏大,175、200次冻融下的抗折强度预测值略微偏小,抗折强度试验值与预测值平均误差率为3.15%。NC强度特性预测符合实际试件的冻融劣化规律,且准确性较高。

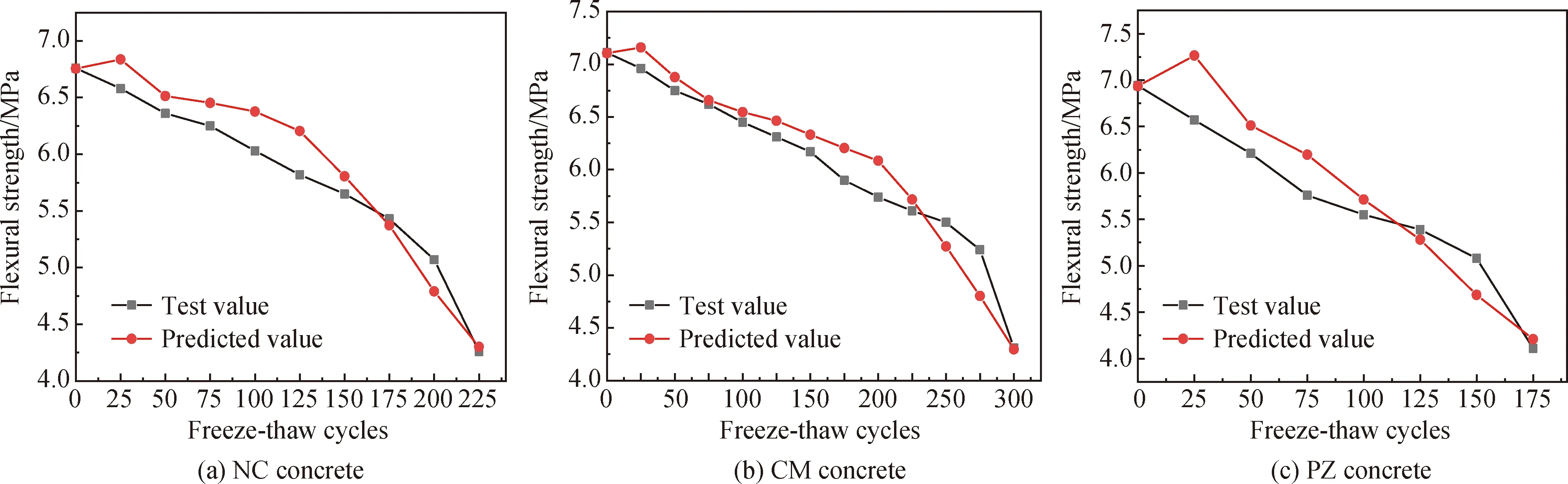
图9 冻融循环下纤维混凝土抗折强度试验值与预测值

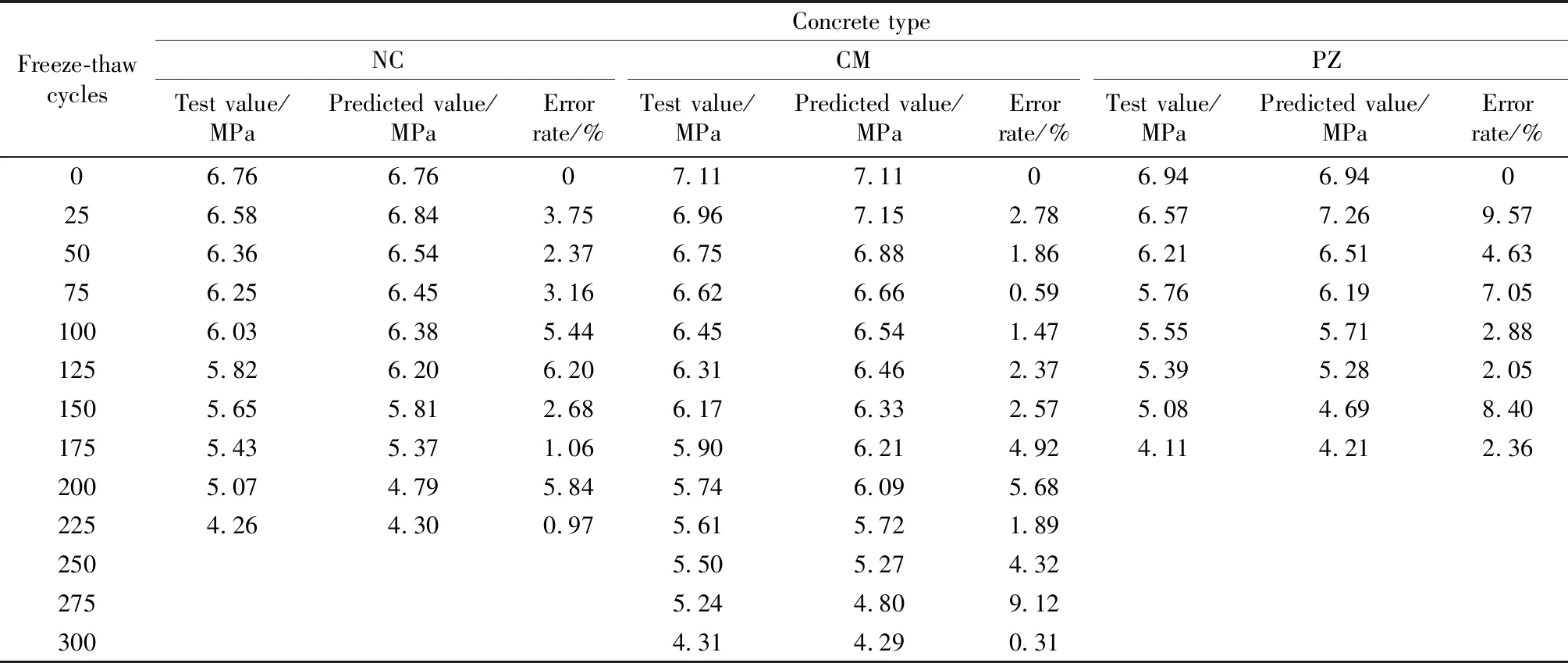
表3 不同冻融循环次数下的纤维混凝土强度损伤误差分析

对CM的抗折强度准确性分析,将冻融循环0～300次的相对动弹性模量数据代入式(14),得到表3,从预测准确性来看,在第275次冻融循环时,抗折强度试验值与预测值误差最大,误差率为9.12%;在第300次冻融循环时,抗折强度试验值与预测值误差最小,误差率为0.31%。由图9(b)CM试验值与预测值的抗折强度变化图可知,25～225次冻融下的抗折强度预测值略微偏大,250、275、300次冻融下的抗折强度预测值略微偏小,抗折强度试验值与预测值平均误差率为2.91%,与NC平均误差率相比,CM的准确性较高。

对PZ的抗折强度准确性分析,将冻融循环0～175次的相对动弹性模量数据代入式(14),得到表3,随着冻融试验的进行,在第25次冻融循环时,抗折强度试验值与预测值误差最大,误差率为9.57%;在第125次冻融循环时,抗折强度试验值与预测值误差最小,误差率为2.05%。由图9(c)PZ试验值与预测值的抗折强度变化图可知,25～100次以及175次冻融下的抗折强度预测值略微偏大,125、150次冻融下的抗折强度预测值略微偏小,抗折强度试验值与预测值平均误差率为4.62%,与CM平均误差率相比,PZ的平均误差率较大。

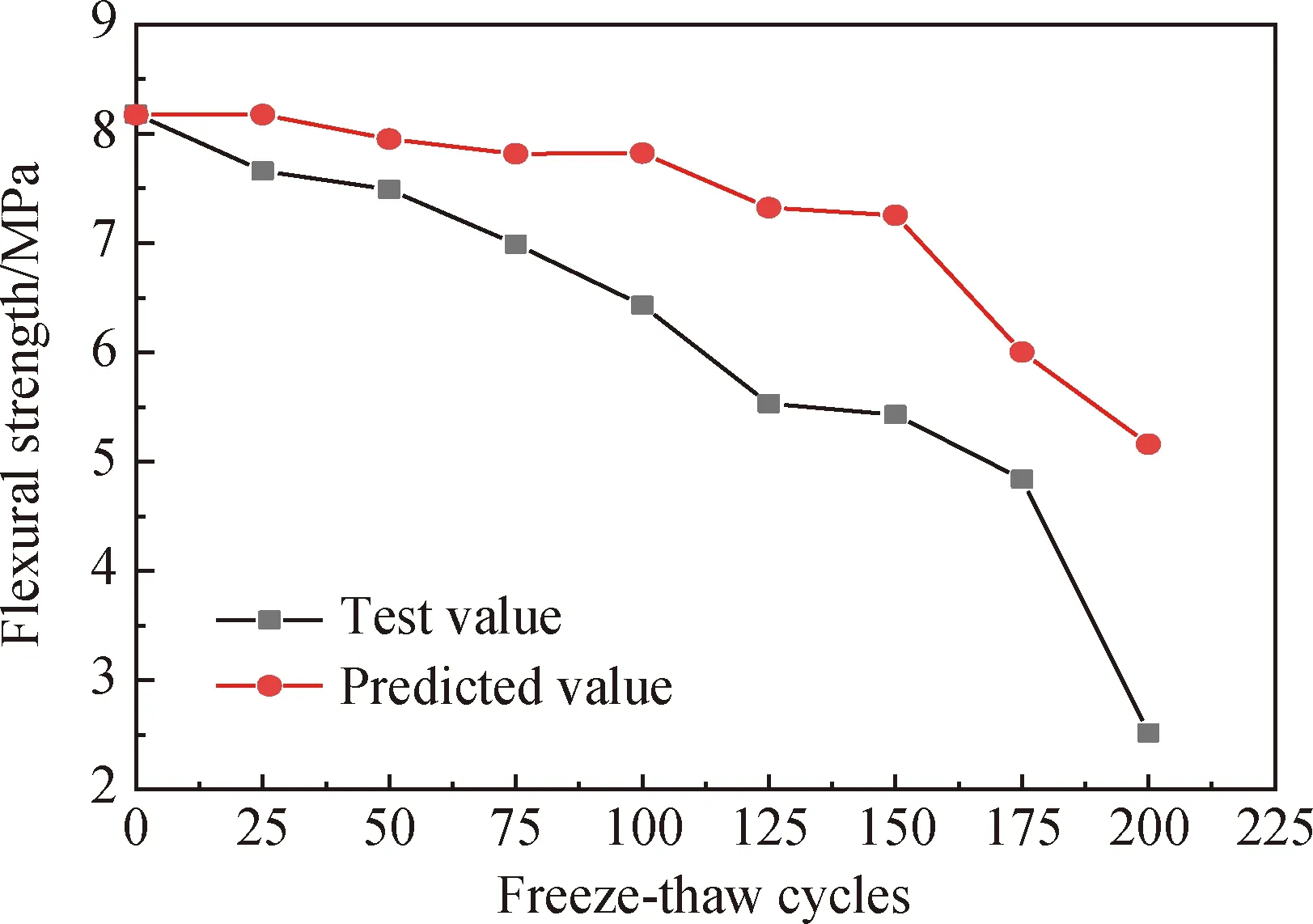
综上所述,三种纤维混凝土的试验值与预测值变化大致相同,初始阶段强度损伤预测值大于试验值,随着冻融次数的增加,强度损伤预测值小于试验值。三种纤维混凝土的抗折强度试验值与预测值平均误差率均小于5%,平均误差率大小排序为CM

3.3 模型验证

为了验证建立损伤模型的适用性和可行性,选用本课题组在青藏高原地区某高速工程项目测定的混凝土试验数据[25]进行验证。该工程位于甘南藏族自治州夏河县,海拔约3 000 m,大气压力约为70 kPa(标准大气压力101.325 kPa)。工程采用的高寒引气混凝土的配合比为m(水泥)∶m(砂子)∶m(水)∶m(碎石)∶m(引气剂)=485∶160∶633∶1 032∶0.05。拟采用高寒引气混凝土试验数据冻融循环0～200次的相对动弹性模量和0次的抗折强度进行验证,将试验数据代入抗折强度预测式(14),得到高寒引气混凝土试验数据冻融循环0～200次的抗折试验值与预测值变化,如图10所示。

图10 高寒引气混凝土抗折强度试验值与预测值

通过抗折强度损伤误差分析和图10的抗折强度试验值与预测值的变化可知,随着冻融次数的增加,高寒引气混凝土的抗折强度预测值与实际试验值的误差大小呈先增大后减小再增大的变化趋势。整体上,预测值比实际试验值偏大。冻融试验后,冻融循环50次的抗折强度试验值与预测值误差最小,误差率为5.82%;在冻融循环200次时,抗折强度试验值与预测值误差最大,误差率为51.16%;抗折强度试验值与预测值的平均误差率为17.86%,预测的高寒引气混凝土抗折强度数值整体偏大,原因是高寒引气混凝土与本试验建立的模型的试验配合比不同。高寒引气混凝土抗折强度试验值与预测值的平均误差率小于18%,表明基于动弹性损伤模型的抗折强度预测对于其他海拔下的混凝土强度劣化规律是适用且可行的。

4 结 论

1)通过分析NC、CM、PZ的冻融试验结果可以看出,CM的质量损失率最小,相对动弹性模量和超声波速下降最平缓,抗折强度最大,而PZ相反。由此可见,而掺入膨胀剂的PZ在改善抗冻性能方面较差,而掺入抗冲磨剂的CM在改善抗冻性能方面较好。

2)对基于模型的抗折强度预测方程分析,NC、CM、PZ三种材料的抗折强度预测值与试验值的变化趋势为,首先预测值大于试验值,随着冻融循环次数的增加,预测值小于试验值。三种纤维混凝土的抗折强度试验值与预测值平均误差率均小于为5%,平均误差率大小排序为CM

3)本文考虑了高原高寒地区低气压的影响,引入气压影响系数,建立了动弹模损伤模型和基于模型的抗折强度预测方程。从工程验证结果看,引气混凝土的抗折强度试验值与预测值误差最小出现在第50次冻融循环,误差率5.82%;试验值与预测值误差最大出现在第200次冻融循环,误差率51.16%;试验值与预测值平均误差率为17.86%。因此,本文建立的动弹性损伤模型和基于模型的抗折强度预测方程是合理且可行的。