钢-PVA混杂纤维增强工程水泥基复合材料弯曲性能研究

张品乐,邓 让,胡 静,吴 磊,陶 忠

(昆明理工大学建筑工程学院,昆明 650500)

0 引 言

传统混凝土材料抗拉强度低、韧性差的缺陷一方面限制了工程结构在恶劣环境下的应用,另一方面也制约了结构的整体抗震性能。工程水泥基复合材料(engineered cementitious composites, ECC)由Li等[1]在20世纪90年代研发,很大程度上克服了混凝土的以上弱点。与普通混凝土在应力条件下表现的脆性不同,ECC具有与金属材料相似的应变硬化现象,裂缝形态呈多重开裂现象,且极限拉伸应变在3%以上,是普通混凝土的300～500倍[2-3]。

相较于其他种类的合成纤维,聚乙烯醇纤维(PVA)有较高的弹性模量和抗拉强度,因此PVA纤维增强工程水泥基复合材料得到了广泛研究与应用[4]。而随着对ECC研究的深入和工程应用,发现单一纤维增强体系不能很好地适应复杂的实际工程环境,两种或多种纤维混掺制备的高延性水泥基复合材料具有显著优势,即在水泥基配比相同的情况下采用混杂纤维的力学性能明显优于单一纤维,这种现象被称为纤维混杂效应[5-6]。王振波等[7-9]通过试验研究不同纤维掺量下钢-PVA纤维ECC破坏形态和力学性能,建立了基于纤维桥接应力理论模型的混杂纤维复合材料应力-裂纹宽度关系和抗弯力学性能预测模型。曹明莉等[10-11]在钢纤维与日产PVA纤维的基础上引入微米级的碳酸钙晶须,配制出能在不同尺度上发挥多水平阻裂作用的三元混杂纤维增强水泥基材料,加入碳酸钙晶须后的水泥基材料在降低了生产成本的同时仍具有优良的应变硬化特征。

除了材料的力学性能外,ECC的材料成本对其在土木工程领域的大规模应用也至关重要。日产PVA纤维的市场价格(约260元/kg)是国产PVA纤维(约45元/kg)的6倍,这极大限制了日产PVA-ECC在工程中的应用[12]。潘钻峰等[13]和乔治等[14]对日产PVA纤维和国产PVA纤维按固定比例混合,配制出成本较低的混杂PVA-ECC材料并研究了混杂PVA-ECC材料的力学性能,但由于试验组设置较少,未能进一步研究纤维掺量对ECC材料工作性能的影响及经济性分析。所以本文基于前人的研究成果,制备了一种钢纤维(SF)、日产PVA纤维(PVA-K)、国产PVA纤维(PVA-C)多元混杂纤维增强工程水泥基复合材料(multicomponent hybrid fiber engineered cementitious composites, MFECC),研究国产PVA纤维替代率对MFECC弯曲性能的影响,评价MFECC的弯曲韧性和性价比,并建立非线性回归模型对MFECC的极限弯曲性能进行分析。

1 实 验

试验中水泥基的组成材料包括:云南华新水泥厂的P·O 42.5硅酸盐水泥,密度为3.1 g/cm3;粉煤灰采用贵州兴义电厂生产的一级粉煤灰,表观密度为2.5 g/cm3,烧失量为3.8%;砂为普通河砂,粒径大小为0.15～0.21 mm,细度模数为2.9,密度为2.66 g/cm3;拌合水为实验室自来水;外加剂为山东宏祥建筑外加剂厂生产的聚羧酸高性能减水剂,掺量为胶凝材料质量的0.3%。SF由河北衡水毛勒金属制品有限公司生产,PVA-C由江苏天怡工程纤维有限公司生产;PVA-K是日本Kuraray公司生产的REC-15型PVA纤维。纤维的性能参数见表1。基体按照m(水泥)∶m(粉煤灰)∶m(砂)=1∶1.8∶0.6的比例混合,水胶比为0.2。本次试验共设计了11组配合比,每组配合比制备三个薄板试件,各配合比中的纤维掺量见表2。

表1 纤维的性能参数

表2 纤维的配合比

为使水泥基中的PVA纤维充分分散,采用单卧轴混凝土搅拌机搅拌,将水泥、粉煤灰和河砂干拌2 min,随后将水和减水剂倒入搅拌机,搅拌3 min,然后依次均匀加入PVA-K、SF和PVA-C,每种纤维加入时间间隔为2 min,最后将拌合物搅拌3 min后获得新拌混杂纤维水泥基材料,整体搅拌时间为12 min。拌合物装入模具时模具置于振动台上边振动边加入拌合物,振捣3 min,等待1 d后脱模并在温度为(20±2) ℃水中养护28 d后取出试件进行弯曲性能试验。

四点弯曲、单轴拉伸和立方体抗压试验同步进行。单轴拉伸试验狗骨形试件尺寸如图1所示,立方体抗压试件尺寸为100 mm×100 mm×100 mm,四点弯曲薄板试件制作参照《玻璃纤维增强水泥性能试验方法》(GB/T 15231—2008),尺寸为400 mm×100 mm×15 mm。单轴拉伸和四点弯曲试验在CSS-44100型电子万能试验机上进行加载,二者均采用位移控制方式加载,其中单轴拉伸试验加载速率为0.15 mm/min,通过布置在试件测试段前后的两个引伸计采集数据并取平均值,四点弯曲试验加载速率为0.30 mm/min,通过布置在试件下方的位移计(LVDT)采集试件的跨中挠度,如图2所示。立方体抗压试验在液压式压力机上进行。

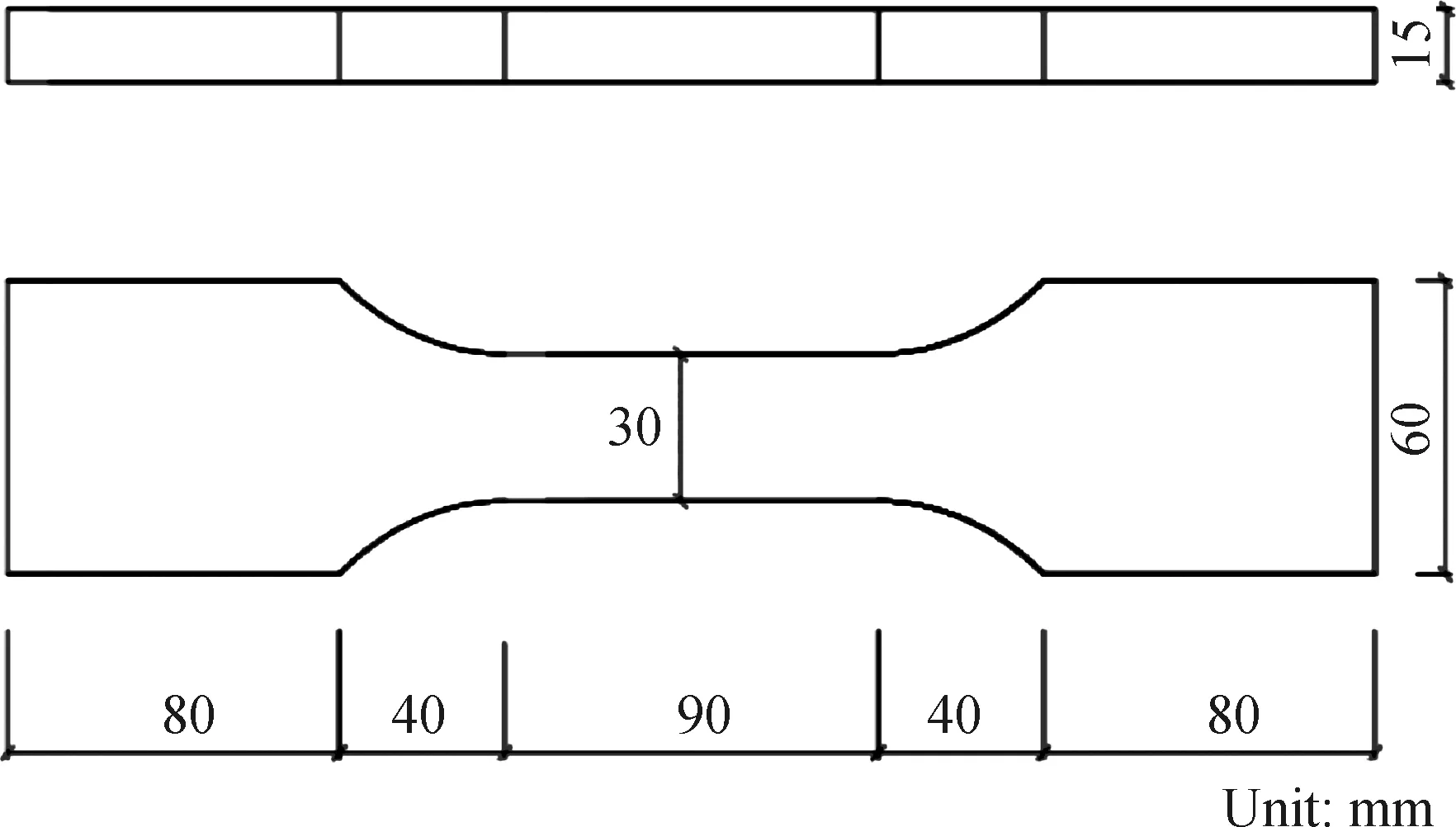
图1 单轴拉伸试验试件

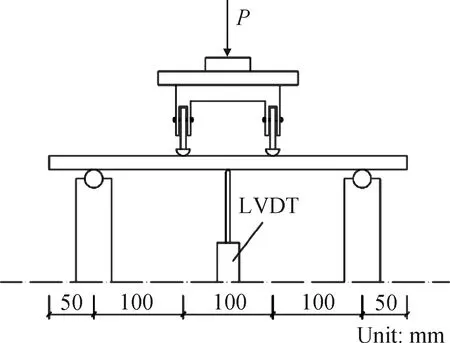
图2 四点弯曲试验示意图

2 结果与讨论

2.1 MFECC单轴力学性能

MFECC的单轴力学性能如表3所示。由表3可知,当SF掺量增加时,MFECC的抗压强度呈先下降后上升的趋势,当PVA-C替代率为25%、SF掺量为0.2%和0.4%(文中掺量均为体积分数)时试件的抗压强度最低。当PVA-C纤维替代率为75%和100%时抗压强度最高。当PVA-C替代率为75%和100%时,PVA纤维与SF能够产生较好的协同作用,MFECC的抗压强度得到提升。当PVA纤维总体积掺量为2.0%时,PVA-C替代率为0%、75%或100%时的抗压强度最高,而当替代率为25%时,抗压强度反而下降。

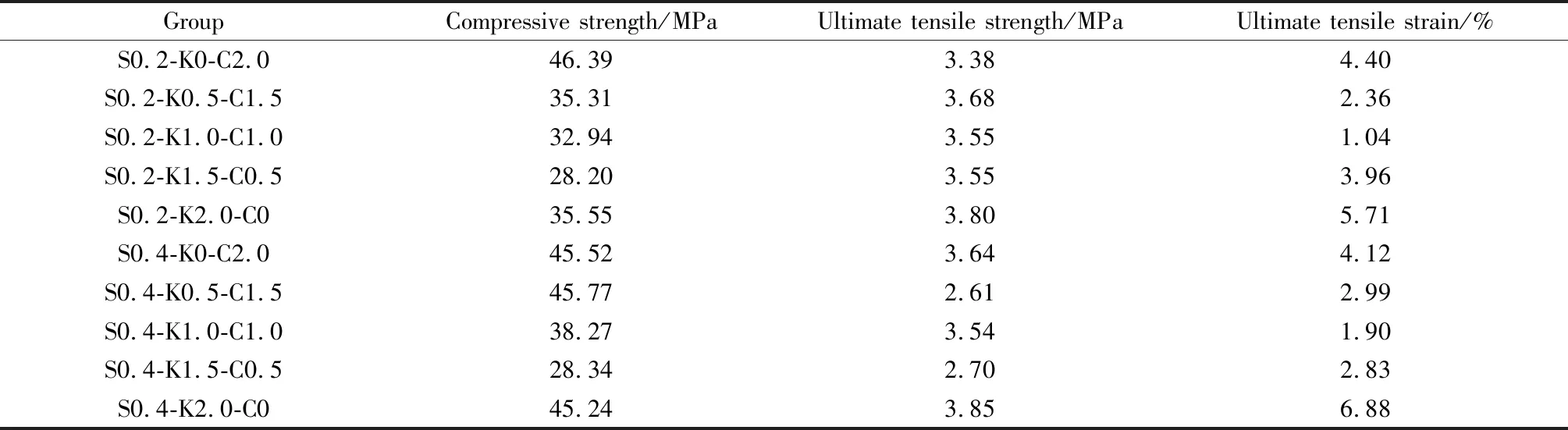
表3 MFECC单轴力学性能

当SF掺量为0.4%时,MFECC的极限拉伸应变最高为6.88%(S0.4-K2.0-C0),最低为1.90%(S0.4-K1.0-C1.0)。其中S0.4-K0-C2.0组的极限拉伸应变为4.12%,极限抗拉强度也可达3.64 MPa。当SF掺量为0.2%时,MFECC的极限拉伸应变最高为5.71%(S0.2-K2.0-C0)。其中S0.2-K0-C2.0组的极限拉伸应变为4.40%,且极限抗拉强度为3.38 MPa。综上所述,PVA-C与SF混杂时,MFECC的极限拉伸应变可达3%,在适当的工程应用条件下,可以选择使用PVA-C代替PVA-K与SF混合,从而降低成本,促进MFECC的应用。

2.2 MFECC荷载-挠度曲线

图3～5为各组配合比试件的荷载-挠度曲线,初裂点为薄板试件荷载-挠度曲线上非线性段的起点。表4为各组配合比试件的弯曲性能指标,包括初裂抗弯强度(初裂强度)和初裂抗弯强度对应的挠度值(初裂挠度)、极限抗弯强度(极限强度)和极限抗弯强度对应挠度(极限挠度)的数据统计。

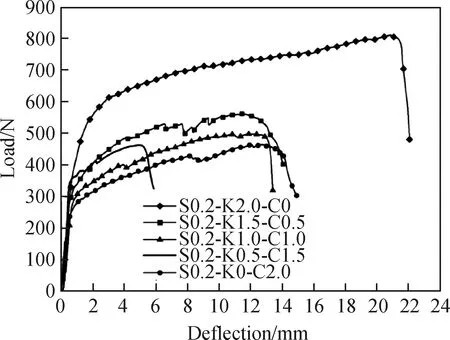
图3 SF掺量为0.2%时MFECC的荷载-挠度曲线

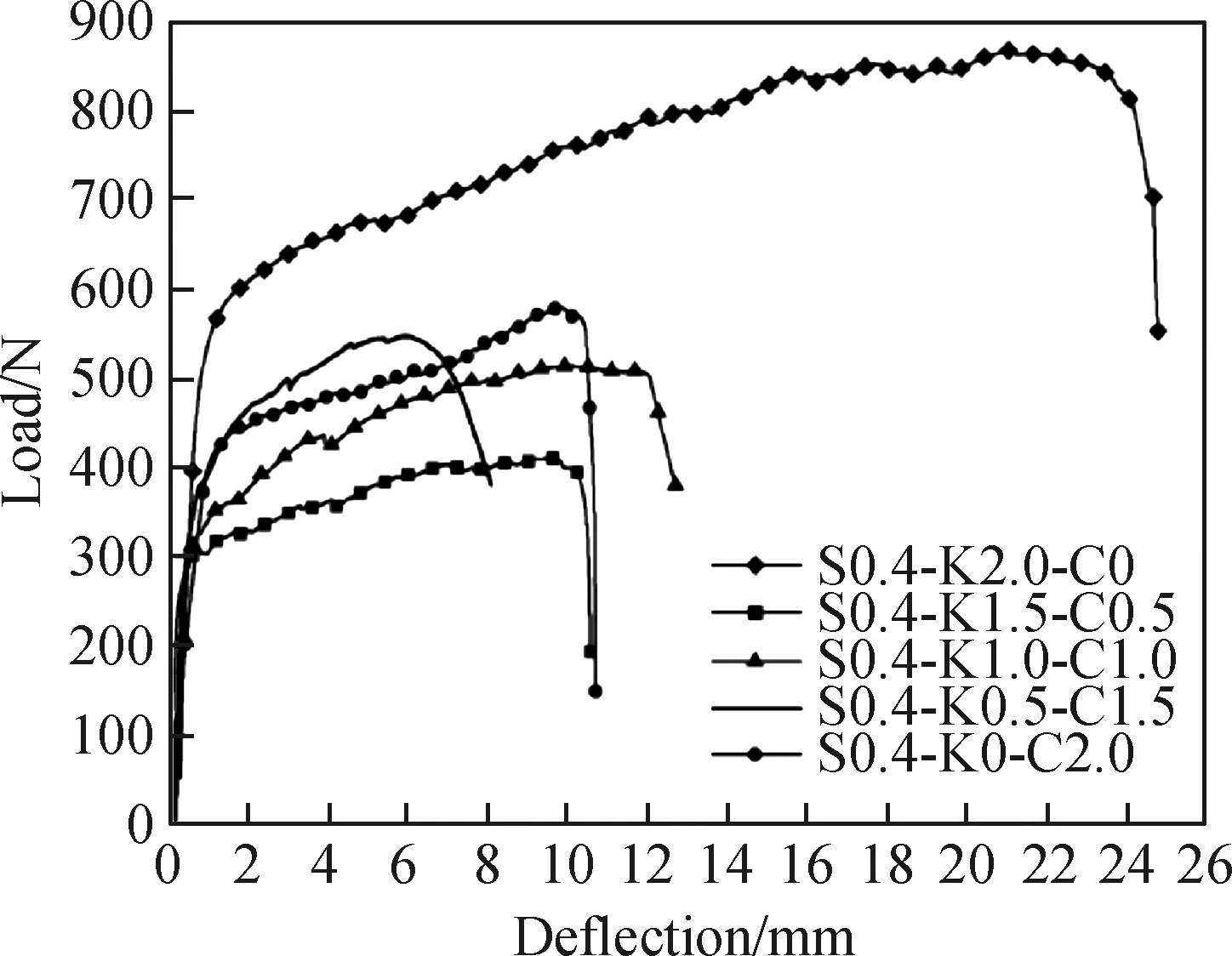
图4 SF掺量为0.4%时MFECC的荷载-挠度曲线

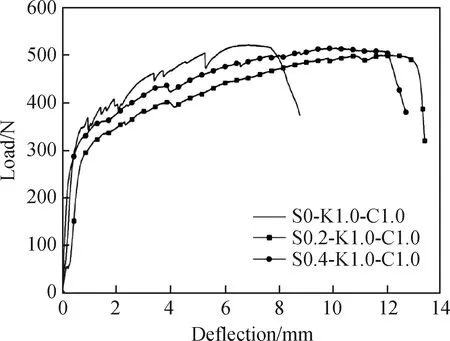
图5 不同SF掺量时MFECC的荷载-挠度曲线

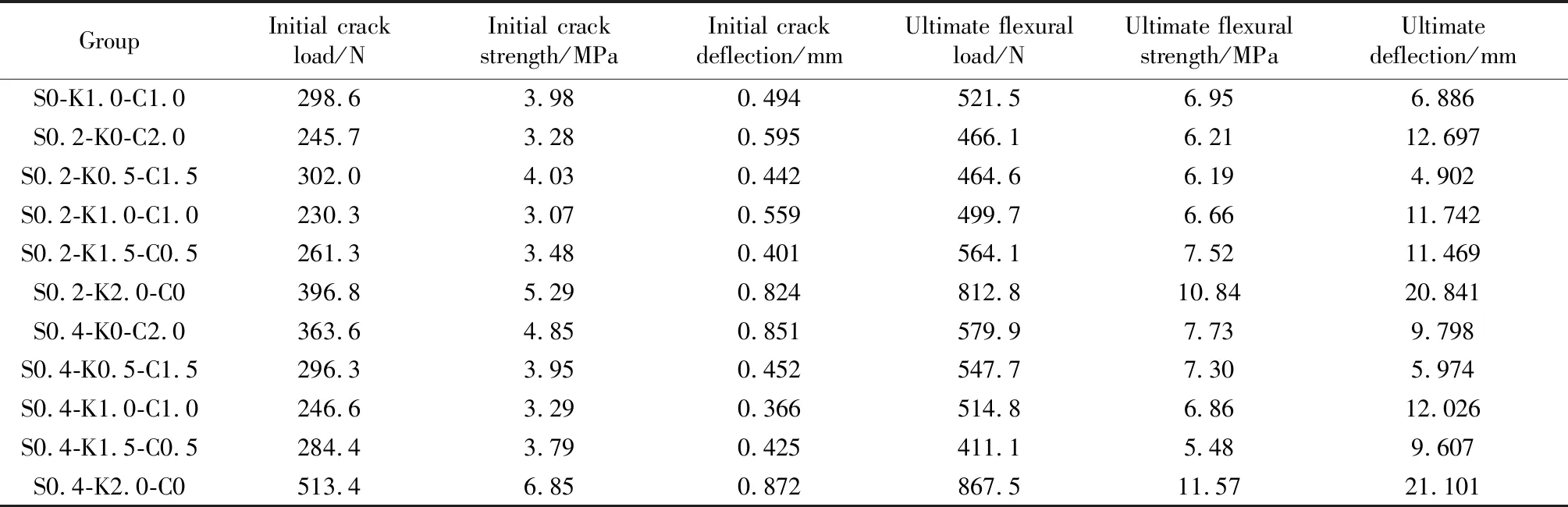
表4 MFECC薄板的弯曲性能指标

不同钢纤维掺量下的MFECC试件荷载-挠度曲线均表现出显著的应变硬化特征,表明两种PVA纤维在MFECC材料的弯曲应变硬化行为中起控制作用。

当PVA-C纤维替代率为0%时,MFECC的弯曲性能最优,而S0.4-K0.5-C1.5和S0.2-K0.5-C1.5组的弯曲性能最低,这是因为相较于PVA-C,PVA-K在表面进行了涂油处理,降低了基体和PVA纤维之间在水化过程中产生的化学粘接,有利于PVA纤维在试件开裂过程中从基体内拔出[15],但PVA-K在经过涂油处理后不仅降低了其亲水性,还增加了纤维的弹性模量,这导致在高替代率下PVA-K(掺量为0.5%)被容易结团的PVA-C包裹,当微裂缝产生时,与2%掺量的PVA-C相比,有效纤维桥接应力偏低[16],所以低掺量PVA-K的MFECC的弯曲性能下降较多。

当掺入0.2%和0.4%SF后,MFECC的极限挠度较未掺SF的S0-K1.0-C1.0分别提升了74.6%和70.5%。这是由于在MFECC体系中,大刚度、高弹性模量的SF掺入后一方面能在搅拌过程中破坏胶凝材料的絮状结构,对成团的PVA纤维起到分散作用[8]。另一方面,PVA纤维还能解决钢纤维在基体中的沉底问题,使SF在MFECC中的分布更加均匀。SF和两种PVA纤维间的正协同作用[17]能在裂纹间发挥良好的桥接作用,从而提高MFECC材料的延性。

2.3 弯曲破坏的裂缝形态

图6为各组试件发生弯曲破坏后纯弯段的裂缝形态。可以看出,MFECC薄板试件在弯曲破坏中表现出了明显的多缝开裂特征,各组试件的弯曲裂缝形态与对应的荷载-挠度曲线所表现出的规律是一致的,随着PVA-K掺量的增加,试件的裂缝宽度和间距明显减小,当PVA-K掺量为2%时,弯曲裂缝极为密集。当PVA-C掺量为2%时,在加载过程中仅有1～2条贯穿型裂缝伴随较少的微裂缝产生,随后贯穿裂缝迅速扩展,试件承载力迅速下降。当掺入PVA-K后,加载条件下薄板试件的纯弯段先形成大量微裂缝,再随着微裂缝的扩展和局部相互贯通,最后形成贯穿型大裂缝,导致试件丧失承载力。就主裂缝的开展情况来看,当PVA-K掺量较多时,贯穿的主裂缝为水平裂缝。当PVA-C掺量较多时,试件的主裂缝路径发生了明显的偏转。这是由于当PVA-C掺量较多时,柔性的PVA-C纤维更容易结团,在试件内部形成缺陷,从而影响主裂缝的发展路径。

图6 MFECC的弯曲破坏形态

2.4 基于弯曲韧性评价的性价比分析

2.4.1 弯曲韧性评价

材料的韧性指数是评价其韧性强弱的重要指标,材料的韧性表示材料在抵抗塑性变形和断裂过程中吸收能量的能力。采用典型的ECC弯曲韧性计算方法计算韧性指数[18],即定义韧性指数为薄板试件弯曲破坏的断裂能与初裂能的比值,能量的大小用荷载-挠度曲线所围成的面积表示,根据荷载-挠度曲线上的初裂荷载和极限荷载所围成的面积可求得初裂能和断裂能。指定弯曲挠度下的弯曲韧性计算与上述方法相同,用T0表示初裂能,T5和T10表示薄板试件跨中挠度为5和10 mm时所吸收的能量,Tf表示断裂能。用公式(1)计算MFECC试件的弯曲韧性指数ηf。

(1)

表5是不同纤维配合比下MFECC的弯曲韧性指标值。由表5可知:

1)对比各试验组试件在不同挠度下的断裂能,从T0到T5和T10的断裂能均稳定增长,表明MFECC试件具有稳定的应变硬化特征。当SF掺量为0.2%和0.4%、PVA-K掺量为0%时试件的初裂能均高于PVA-K和PVA-C混掺时的初裂能,这是因为亲水的PVA-C在纤维基体内不易被拔出,在试件开裂时需要吸收更多的能量。

2)对于ηf而言,MFECC薄板试件的弯曲韧性指标与荷载-挠度中极限弯曲性能的变化情况不一致,S0.4-K2.0-C0组的断裂能明显高于S0.4-K1.5-C0.5组,然而两组的弯曲韧性指数仅相差5.827 4。在试验过程中发现S0.4-K2.0-C0组试件在出现裂缝时的荷载-挠度曲线仍然处于线性增长段,这是因为随着PVA-K掺量增多,试件韧性随之增强,在弯曲荷载作用下早期裂缝多为细密的裂缝(见图4),试件每次开裂所释放的能量也较小,只有当裂缝开展后释放的能量增加,曲线才表现出明显的应变硬化特征,因此荷载-挠度曲线上的初裂挠度与初裂荷载是比实际值偏大的,最终导致试件的弯曲韧性指标偏低。

3)当SF掺量为0.2%时,MFECC的弯曲韧性指数平均值为78.96,大于在SF掺量为0.4%时的弯曲韧性指数平均值58.95,说明在钢纤维体积掺量为0.2%和0.4%的两个系列中,前者的整体弯曲韧性更好。

2.4.2 性价比分析

价值工程(value engineering, VE)是以产品或者作业的功能分析为核心,以提高产品或作业的价值为目的,力求以最低寿命周期成本实现产品或者作业必要功能的一项有组织的创造性活动[19]。材料成本和材料的功能(性能)是建筑材料在应用过程中的决定性因素,因此本文将VE应用于建筑材料的生产阶段,基于弯曲性能对MFECC材料进行性价比分析。根据价值工程的基本原理,价值、性能和成本的关系如式(2)所示[19]。

(2)

式中:V为MFECC材料的价值系数,价值系数越高,性价比越高;F为MFECC材料的性能;C为材料的生产成本。MFECC薄板四点弯曲的荷载-挠度曲线中对初裂强度和初裂挠度的选取主观性较强,所以初裂点的选取存在较大误差,由式(1)可知,初裂点的选取误差对弯曲韧性指数有较大影响,因此对于公式(2)中的F在本文中用断裂能Tf表示。对于材料的生产成本C,由于基体配合比相同,对MFECC价值的影响因素仅为不同纤维的掺量,纤维的成本采用价格比CPVA-K∶CPVA-C∶CSF=260∶45∶7.8表示,并根据不同配合比下的纤维掺量进行加权计算。由于试件的断裂能较小,为直观地表现MFECC材料的价值系数变化趋势,对计算结果的价值系数进行放大处理。

图7表示不同纤维配合比下MFECC的价值系数,PVA-C全部替代PVA-K时的价值系数在同SF掺量系列中最高,这说明PVA-C在MFECC体系内的力学性能远不如PVA-K,但其经济性优于PVA-K。而随着PVA-C对PVA-K的替代率降低(PVA-C掺量由1.5%降低到0%),MFECC的价值系数整体呈增长趋势,尤其在SF的掺量为0.2%时,价值系数分别增长了60.05%、31.59%和173.53%。故PVA-C替代PVA-K配制的MFECC材料仍然具有一定的性价比。

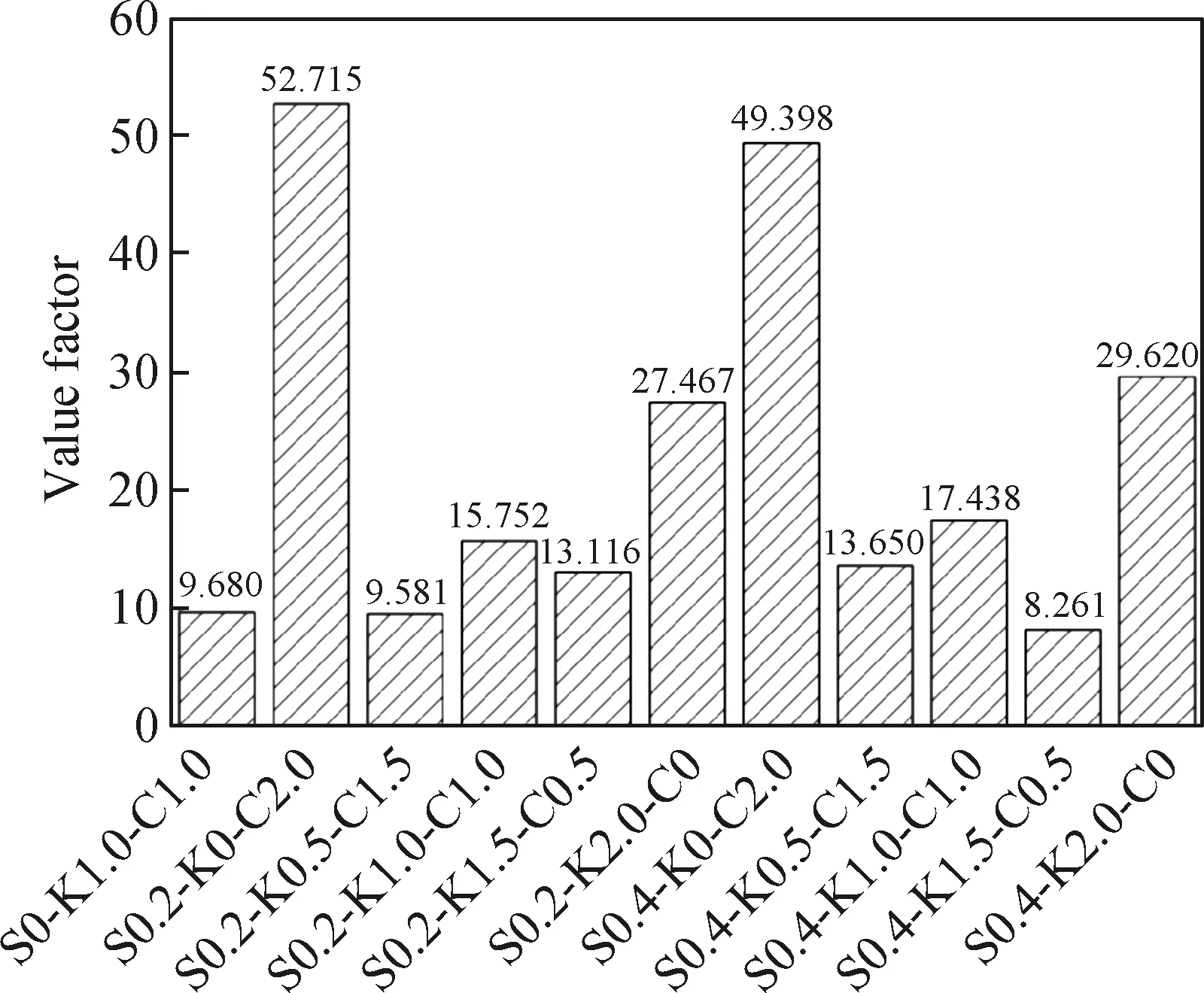
图7 不同纤维配合比下MFECC的价值系数

综上所述,若仅考虑MFECC材料在弯曲荷载作用下的力学性能,使用PVA-C替代PVA-K具有良好的经济性,当PVA-C完全替代PVA-K时具有最佳性价比,S0.2-K0-C2.0组的性价比最高。需要说明的是,建筑材料的成本与力学性能之间的关系不是线性的,存在明显的边际效用递减规律,即当力学性能超出一定的提升范围后,材料成本将迅速增加,因此MFECC的性价比分析需要考虑工程应用中的力学性能需求。

2.5 极限弯曲性能的回归分析

2.5.1 建立预测模型

由于MFECC薄板四点弯曲的初裂点选取存在较大误差,本节中仅对试件的极限弯曲强度与极限挠度进行回归分析。所采用的分析方法为非线性回归分析法,此方法是通过计算机语言对所建立的预模型进行多次数据迭代,迭代的步骤和数量取决于试验中自变量的数量。本试验中所涉及到的自变量为PVA-K掺量、PVA-C掺量和SF掺量,由于PVA-C和PVA-K的总体积掺量为2%,所以本节中选取的自变量为PVA-K掺量和SF掺量。在许开成等[20]的研究基础上经过多次对比,确定以下预测模型。

对于极限抗弯强度,建立的预测模型如式(3)所示。

模型1:

y=a1+b1α5+c1β5+d1α4+e1β4+f1αβ

(3)

对于极限挠度,建立的预测模型如式(4)所示。

模型2:

z=a2+b2α2+c2β2+d2α+e2β+f2αβ

(4)

式中:y为MFECC极限抗弯强度预测值;z为MFECC极限挠度预测值;α为SF掺量;β为PVA-K纤维掺量;ai,bi,ci,di,ei,fi(i=1,2,分别代表模型1、模型2)为预测模型参数,均为常数值。

2.5.2 预测模型结果

经过SPSS软件对模型1进行非线性回归分析后,其数学表达式如式(5)所示。

y=956.191α5+0.459β5-362.455α4-0.578β4-2.413αβ+7.069R2=0.903 00

(5)

图8为模型1的残差图。由图8可知,数据点均匀地随机分布在0附近,且预测值的相对误差最大值为12.04%,在可接受的误差范围(15%)内[20]。图9为模型1的试验值与预测值的对比图。极限抗弯强度的试验值和预测值的数据点拟合曲线斜率为0.934 168,接近1,且R2为0.905 46,表明模型1的预测值能准确地预测弯曲强度试验值。

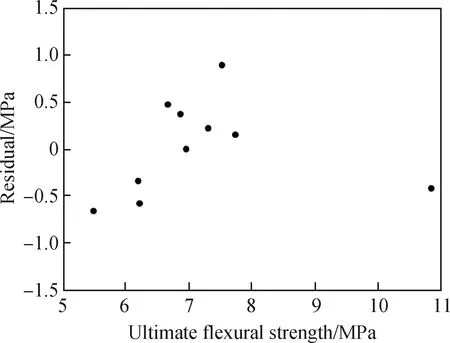
图8 模型1的残差图

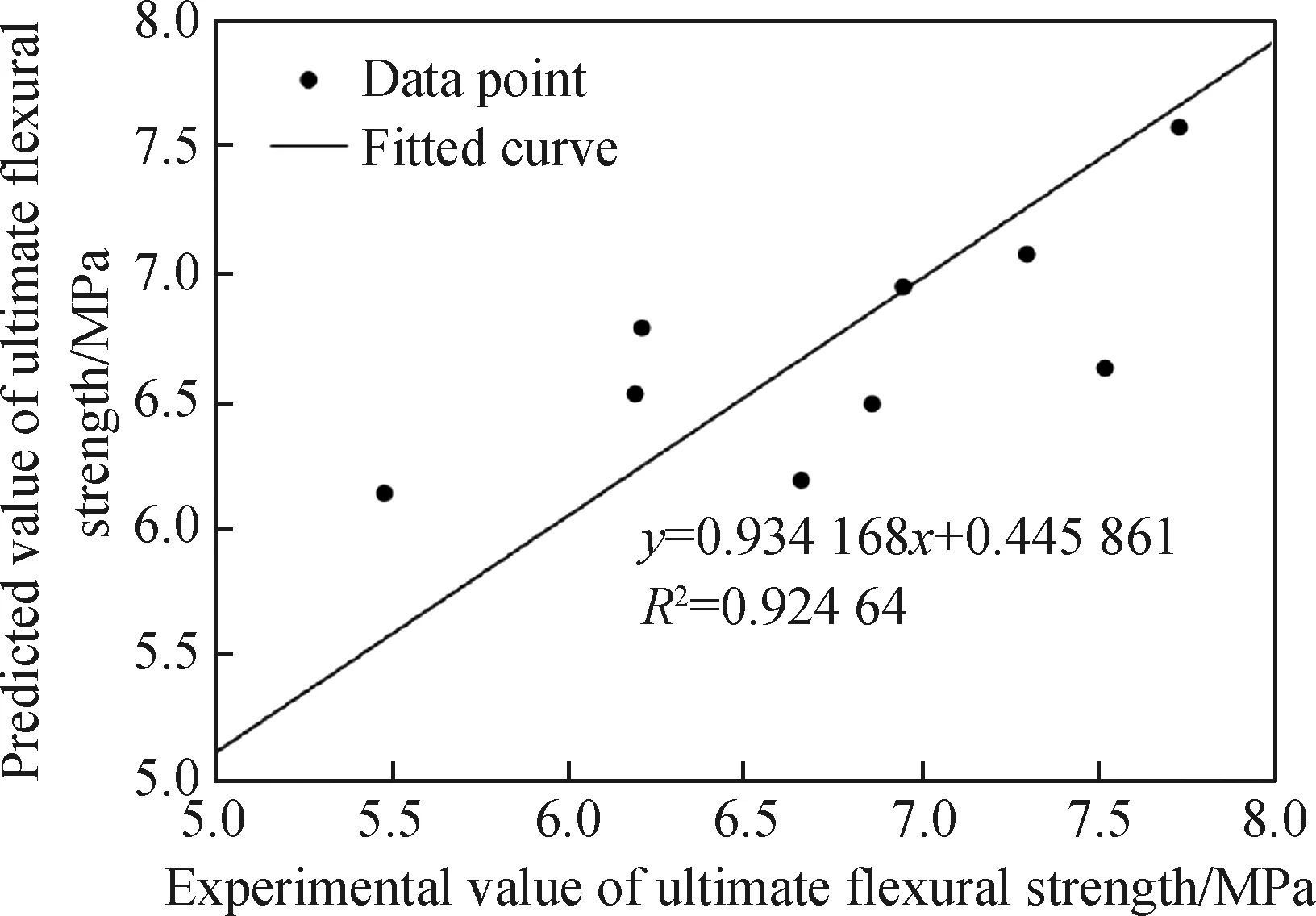
图9 模型1的试验值与预测值对比

模型2回归后的数学表达式如式(6)所示。

y=-31.752α2+7.056β2+12.521α-10.219β+3.39αβ+10.054R2=0.824 00

(6)

图10为模型2的残差图,其残差分布与模型1相似,仍随机分布在0的附近,但分布较模型1分散。可见模型2虽然能用于MFECC的极限挠度的预测,但精度有所下降。图11为模型2的预测值与试验值对比图。预测值和试验值对比数据分布在斜率为0.916 222的直线附近,拟合出的直线R2为0.949 27,因此模型2也具有较高的预测精度。

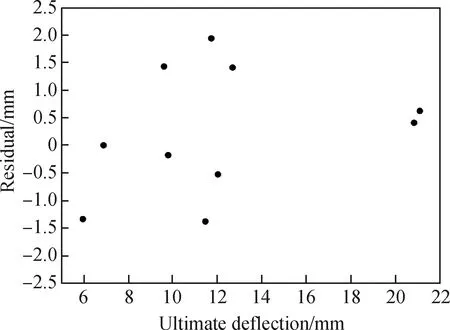
图10 模型2的残差图

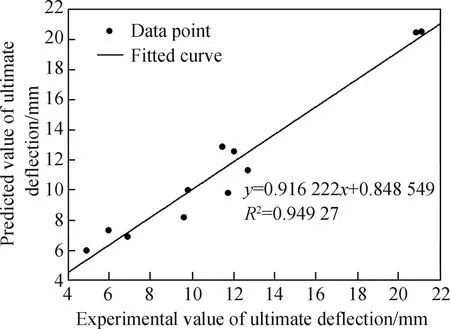
图11 模型2的试验值与预测值对比

综上所述,基于SPSS软件建立的MFECC材料极限弯曲性能预测模型对弯曲试验结果具有良好的拟合度。

3 结 论

1)在MFECC体系中日产PVA纤维对弯曲性能起控制作用,钢纤维对MFECC材料弯曲性能的增强作用明显。

2)MFECC材料表现出显著的应变硬化力学行为,薄板试件多缝开裂现象随着国产PVA纤维替代率的降低而增强,当国产PVA纤维的替代率为0%时,MFECC试件呈多缝开裂现象,具有极高的延性和弯曲强度。

3)MFECC材料中使用国产PVA纤维部分替代日产PVA纤维具有良好的性价比,在一定的材料性能范围内,当钢纤维、日产PVA和国产PVA纤维体积掺量分别为0.2%、0%和2.0%时,MFECC的性价比最高。

4)建立的MFECC极限弯曲性能非线性回归模型有较高的拟合精度。