考点早知道,知识全掌握——基于函数模块的应用

■江苏省海门中学 陆莉婷

函数是贯穿整个高中数学知识体系的一条主线,成为历年高考数学试卷中的一大重要知识点与考查点。函数模块的考查,是基于基本初等函数,借助函数的概念、定义域与值域,函数的表示与图像,函数的基本性质,分段函数与抽象函数,函数的零点与函数的实际应用等各个方面,从不同知识点来切入与设置。下面结合2023年高考真题,就函数模块的常见考点加以剖析,使同学们对高考考点早知道,函数知识全掌握。

一、函数的定义域或值域

例1(2023 年高考数学上海卷·5)已知f(x)=则f(x)的值域是____。

分析：根据题设条件,通过分段函数对自变量在不同情况下确定对应函数的取值情况,综合归纳来确定函数的值域。注意分段函数场景下的函数值域是各自情况下的函数值域的并集。

解：当x＞0时,f(x)=2x＞20=1;

当x≤0时,f(x)=1。

综上可知,函数f(x)的值域为[1,+∞)。

点评:求解函数的值域问题,可根据函数的解析式,结合一些常见的值域求解方法来分析与处理。这里涉及分段函数的值域问题,要注意分类讨论,并与集合的运算加以联系与综合。

二、函数的图像

例2(2023 年高考数学天津卷·4)函数f(x)的图像如图1所示,则f(x)的解析式可能为( )。

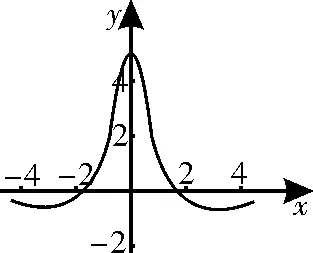
图1

分析：根据题设条件,借助函数的图像的对称性来确定函数的奇偶性,由此排除一些不满足条件的选项;在此基础上,借助函数的图像与y轴的交点坐标,可得f(0)=5,又可以进一步排除不满足条件的选项,从而达到目的。

解：由图1可知,函数f(x)的图像关于y轴对称,所以函数f(x)为定义域上的偶函数,由此可以排除选项A、B;而f(0)=5,由此可以排除选项C。

故选D。

点评:解决涉及函数图像的综合应用问题,往往要从函数的图像入手,抓住函数图像的结构特征,从图像的对称性、图像的最高点与最低点、图像的增减变化趋势等层面入手,进行正确分析与判断。往往可以借助特殊值思维、极限思维等加以渗透与应用。

三、函数的基本性质

例3(2023 年高考数学新高考Ⅰ卷·4)设函数f(x)=2x(x-a)在区间(0,1)上单调递减,则a的取值范围是( )。

A.(-∞,-2] B.[-2,0)

C.(0,2] D.[2,+∞)

分析：根据题设条件,合理分拆题设中的复合函数,从复合函数的单调性入手,巧妙结合指数函数、二次函数的图像与性质,合理构建相应的不等式,进而得以确定参数的取值范围。

解：依题知,函数f(x)=2t在区间(0,1)上单调递增。结合复合函数的单调性,可知函数t=x(x-a)=在区间(0,1)上单调递减。结合二次函数的图像与性质,可知对称轴x=≥1,解得a≥2,即a的取值范围是[2,+∞)。

故选D。

点评:常见的函数的基本性质主要包括奇偶性、单调性、周期性、对称性等,问题的设置,有时单一性质直接考查,有时多个性质综合考查。而涉及复合函数的基本性质问题,也是考查中的一个重点与难点,要加以高度重视。

四、函数的零点

例4(2023 年高考数学新高考Ⅰ卷·15)已知函数f(x)=cosωx-1(ω＞0)在区间[0,2π]上有且仅有3个零点,则ω的取值范围是____。

分析：根据题设条件,由函数的零点问题转化为相应的方程,结合自变量的取值限制,余弦函数的图像与性质确定方程的解的取值问题,数形结合确定变量的取值情况,进而确定参数的取值范围。

解：令f(x)=cosωx-1=0,则cosωx=1。因为x∈[0,2π],所以ωx∈[0,2ωπ]。要使得函数f(x)=cosωx-1(ω＞0)在区间[0,2π]上有且仅有3 个零点,则cosωx=1在ωx∈[0,2ωπ]上有且仅有3 个解,所以4π≤2ωπ＜6π,解得2≤ω＜3,即ω的取值范围是[2,3)。

例5(2023 年高考数学全国乙卷文科·8)若函数f(x)=x3+ax+2存在3个零点,则a的取值范围是( )。

A.(-∞,-2) B.(-∞,-3)

C.(-4,-1) D.(-3,0)

老三这时也看到了孔老一，连滚带爬冲了过来，也不说话，见面就跪：“哥，哥，咱爸过山去了。”说罢便伏地嚎啕大哭说罢便伏地号啕大哭。

分析：根据题设条件,通过求导,结合参数的取值情况加以分类讨论,并结合函数的单调性与极值的确定,利用函数存在3 个零点,构建相应的涉及极大值与极小值的不等式组,进而得确定参数的取值范围。

解：依题得f'(x)=3x2+a。

若a≥0,则f'(x)≥0,函数f(x)在定义域R上单调递增,故不存在3个零点,不符合题意,舍去。

所以a的取值范围是(-∞,-3)。

故选B。

点评:涉及函数的零点问题一直是高考中考查的一个基本知识点,涉及零点个数的确定,零点所在区间的判断,参数的最值或取值范围等问题。特别对于以上函数的零点问题,经常转化为相应的方程的根、函数的图像的交点等相关问题来化归与转化。

五、抽象函数问题

例6(2023 年高考数学新高考Ⅰ卷·11)(多选题)已知函数f(x)的定义域为R,f(xy)=y2f(x)+x2f(y),则( )。

B.f(1)=0

C.f(x)是偶函数

D.x=0为f(x)的极小值点

分析：根据题设条件,结合抽象函数的关系式,利用特殊值的赋值法处理来分别确定选项A、B、C 的真假;并结合关系式的特征,借助特殊函数的构建来举例说明其是错误的,由此判断正确选项。

解：令x=y=0,则f(0)=f(0)+f(0)=2f(0),解得f(0)=0,故选项A 正确;

令x=y=1,则f(1)=f(1)+f(1)=2f(1),解得f(1)=0,故选项B正确;

令x=y=-1,则f(1)=f(-1)+f(-1)=2f(-1),解得f(-1)=0,单令y=-1,则f(-x)=f(x)+x2f(-1)=f(x),即f(x)是偶函数,故选项C正确;

综上分析,故选ABC。

点评:该题是抽象函数的判断与应用问题,选项A、B、C 三者层层递进,这也是问题设置的一个合理安排,给考生一个思维过程与深入研究过程。而对于选项D 的判断,还可以直接举例:取常值常数f(x)=0,此时满足条件,而此时函数f(x)不存在极小值点,其是错误的。

六、函数的实际应用

例7(2023 年高考数学新高考Ⅰ卷·10)(多选题)噪声污染问题越来越受到重视。用声压级来度量声音的强弱,定义声压级Lp=20×,其中p0(p0＞0)是听觉下限阈值,p是实际声压。表1 为不同声源的声压级:

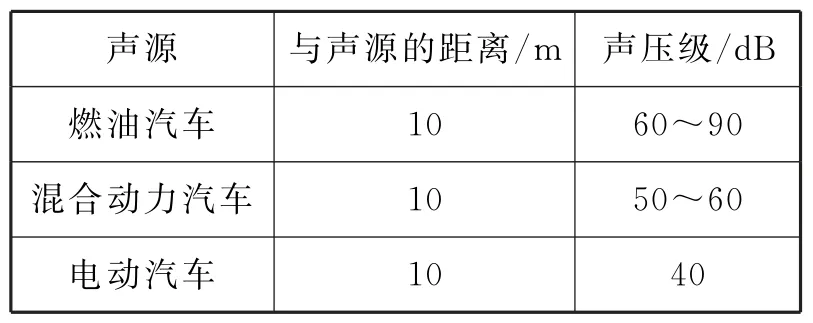
表1

已知在距离燃油汽车、混合动力汽车、电动汽车10 m 处测得实际声压分别为p1、p2、p3,则( )。

A.p1≥p2B.p2＞10p3

C.p3=100p0D.p1≤100p2

分析：根据题设条件,通过创新定义声压级的对数关系式,结合相应的数据信息,通过作差法,并结合对数运算及不等式的性质来分析与求解,逐个判断相关选项的真假情况,进而得以实际应用。

综上分析,故选ACD。

点评:解决涉及函数的实际应用问题,关键在于正确阅读理解并挖掘题目的内涵与实质,结合函数、不等式等的应用来分析。破解此类实际应用问题要注意把握其中的基本问题,同时要符合生活实际。

历年高考对函数模块知识的考查,往往都是以二次函数、幂函数、指数函数和对数函数等基本初等函数为载体,借助运算、解析式、图像、性质、应用等来合理设计,巧妙交汇与整合一些相关知识点,主要出现在选择题或填空题中,难度属于较易或中等。