“集合和常用逻辑用语、函数、导数及其应用”跟踪练习参考答案
一、单选题
1.B 2.C 3.A 4.B 5.D 6.C
7.C 8.A 9.D 10.A 11.D 12.D
13.C 14.D 15.D 16.D 17.C
18.C 19.D 20.C
二、多选题
23.AD
24.AD 提示:由f(x)的图像关于x=2对称可得f(x+4)=f(-x),再由f(x)为偶函数可得f(-x)=f(x),故f(x)=f(x+4),即f(x)的周期为4,故A 正确。当x∈[0,2]时,由f(x)=x2可得f(x)在[0,2]上单调递增,故f(x)在[8,10]上单调递增,故B 错误。又f(0)=0,f(2)=4,故f(x)的值域为[0,4],故C 错误。在同一坐标系下画出函数y=f(x)与y=4loga(x+5)(a>1)的图像,如图1所示。由图可知,要使y=f(x)与g(x)=4loga(x+5)在[-4,6]上恰有5个不同交点,只需解得7<a<11,即a的取值范围为(7,11),故D 正确。
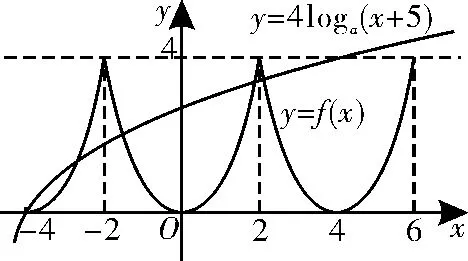
图1
三、填空题
26.1 27.8 28.24x-y-32=0
29.-1或1 30.①②③ 31.(-∞,0)
32.[1,+∞) 33.m≤-1或m>
34.6 35.4 36.3 37.3
43.②③④ 提示:因为f(x)=x(x-3)2,所以f'(x)=3x2-12x+9=3(x-3)·(x-1)。令f'(x)>0,解得x>3或x<1,所以f(x)的单调递增区间为(-∞,1)和(3,+∞);令f'(x)<0,解得1<x<3,所以f(x)的单调递减区间为(1,3)。又f(0)=0,f(3)=0,f(1)=4,故f(x)(x≥0)的图像如图4所示。设f(a)=f(b)=f(c)=t,则0<t<4,0<c<1<b<3<a<4,故①错误。又f(x)-t=(x-a)(xb)(x-c),故x(x-3)2-t=(x-a)(x-b)(x-c),即x3-6x2+9x-t=x3-(a+b+c)x2+(ab+ac+bc)x-abc,对照系数得a+b+c=6,故③正确。abc=t∈(0,4),故④正确;因为3<a<4,所以3<6-(b+c)<4,解得2<b+c<3,故②正确。
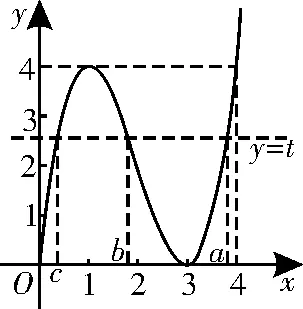
图4
四、解答题
45.(1)由x2-7x-18≥0,解得A=(-∞,-2]∪[9,+∞)。
由4-3x-x2>0,解得B=(-4,1)。
由∁UA=(-2,9),可得(∁UA)∩B=(-2,1)。
(2)因为A∩C=C,所以C⊆A。
当C=∅时,m+2≥2m-3⇒m≤5;
当C≠∅时,可得或解得m≥7。
综上可得,实数m的取值范围为(-∞,5]∪[7,+∞)。
46.(1)若p为真命题,则m≤x2-2x在x∈[0,2]上恒成立。因为当x∈[0,2]时,(x2-2x)min=1-2=-1,所以m≤-1,即实数m的取值范围为(-∞,-1]。
(2)对于q,当x≥0 时,2x+3≥1+3=4,要使2x+3=m成立,只需m≥4即可,即m∈[4,+∞)。
由于p,q只有一个为真命题,则可以分类讨论:
当p真q假时,由得m≤-1;
当p假q真时,由得m≥4。
综上所述,实数m的取值范围为(-∞,-1]∪[4,+∞)。
47.(1)由题意易知,f(-x)=f(x),则[f(-x)]'=[f(x)]',即-f'(-x)=f'(x),故f'(x)为奇函数,故g(x)=为奇函数。
因为f(x)+g(x)=2x+1,所以f(-x)+g(-x)=f(x)-g(x)=2-x+1,两式相加得f(x)=2x+2-x,所以g(x)=2x-2-x。
(2)由2[f(x)]2-3g(x)≤8,可得2(2x+2-x)2-3(2x-2-x)≤8,所以2(22x+2+2-2x)-3(2x-2-x)≤8,即2[(2x-2-x)2+4]-3(2x-2-x)≤8。
(2)因为f(mx2-1)+f(2-mx)>0,所以f(mx2-1)>-f(2-mx),因为f(x)为奇函数,所以f(mx2-1)>f(mx-2),所以mx2-1>mx-2,即mx2-mx+1>0。
①当m=0 时,不等式为1>0 恒成立,符合题意;
②当m>0时,有Δ=m2-4m<0,解得0<m<4。
综上可得,实数m的取值范围为[0,4)。
当b≤0时,f'(x)=-x2+b≤0,此时f(x)在R上单调递减,f(x)在R上只有1个零点,不合题意。
所以实数b的取值范围是(0,+∞)。
当a=2,b=-3 时,f(x)=+2x2-3x-6,f'(x)=-x2+4x-3。令f'(x)=-x2+4x-3≥0,解得1≤x≤3,易知x=1是f(x)的极小值点,与题意不符。
当a=-2,b=5 时,f(x)=-2x2+5x-10,f'(x)=-x2-4x+5。令f'(x)=-x2-4x+5≥0,解得-5≤x≤1,易知x=1是f(x)的极大值点,符合题意。
故a=-2,b=5。
因为x∈[-1,3],所以f(x)在[-1,1]上单调递增,在[1,3]上单调递减。
50.(1)已知f(x)=lnx-kx+1,求导得f'(x)=-k(x>0)。
当k≤0时,f'(x)≥0 恒成立,f(x)无极值;
综上可得,当k≤0 时,f(x)无极值;当k>0时,f(x)有极大值=-lnk,无极小值。
(2)若g(x)≥f(x),则x(ex-2)-lnx+kx-1≥0在x>0 时恒成立,所以k≥-ex+2恒成立。
令ω(x)=xex(x>0),则ω'(x)=(x+1)ex>0,故ω(x)在(0,+∞)上单调递增。
所以当x∈(0,x0)时,h(x)单调递增,当x∈(x0,+∞)时,h(x)单调递减,所以h(x)max=h(x0)=+2=+2=1。
所以k≥h(x0)=1,即k的取值范围为[1+∞)。
51.(1)已知x∈R,若f(x)在R上是增函数,则f'(x)=ex-ex-a≥0,即a≤exex在x∈R上恒成立,所以a≤(ex-ex)min。
令g(x)=ex-ex,x∈R,则g'(x)=ex-e,当x>1 时,g'(x)>0,当x<1 时,g'(x)<0,所以g(x)≥g(1)=0,所以a≤0。
(2)已知a∈,不妨设m>n,由题意知f'(x)=0有2个不同的解m,n。
由(1)可知n<1<m,且f'(m)=f'(n)=0,要证<e-1,即证f(m)-(e-1)m<f(n)-(e-1)n。
构造函数h(t)=f(t)-(e-1)t=et--at-(e-1)t,则h'(t)=et-et-a-(e-1)。
因为f'(0)=e0-a>0,f'(2)=e2-2e-a>0,所以0<n<1<m<2。
令m(t)=h'(t),则m'(t)=et-e。
当t>1时,m'(t)>0;当t<1时,m'(t)<0。所以h'(t)在(1,2)上单调递增,在(0,1)上单调递减。又h'(0)=2-a-e<0,h'(2)<0,所以h'(t)<0,所以h(t)在(0,2)上单调递减。
所以h(m)<h(n),即原命题得证。
52.(1)由题意知,f'(x)=(x2-1)exa(x2-1)=(x-1)(x+1)(ex-a)。
若a≤1,则当0<x<1时,f'(x)<0;当x>1时,f'(x)>0。所以f(x)在(0,1)上是减函数,在(1,+∞)上是增函数。
若1<a<e,即0<lna<1,则当0<x<lna或x>1 时,f'(x)>0;当lna<x<1时,f'(x)<0。所以f(x)在(0,lna)上是增函数,在(lna,1)上是减函数,在(1,+∞)上是增函数。
若a=e,则f'(x)≥0 恒成立,所以f(x)在(0,+∞)上是增函数。
若a>e,即lna>1,则当0<x<1或x>lna时,f'(x)>0;当1<x<lna时,f'(x)<0。所以f(x)在(0,1)上是增函数,在(1,lna)上是减函数,在(lna,+∞)上是增函数。
综上所述,当a≤1 时,f(x)在(0,1)上是减函数,在(1,+∞)上是增函数;
当1<a<e时,f(x)在(0,lna)上是增函数,在(lna,1)上是减函数,在(1,+∞)上是增函数;
当a=e时,f(x)在(0,+∞)上是增函数;
当a>e时,f(x)在(0,1)上是增函数,在(1,lna)上是减函数,在(lna,+∞)上是增函数。
当0<x<x0时,h(x)<0,即g'(x)>0;当x0<x<1时,h(x)>0,即g'(x)<0;当x>1时,h(x)>0,即g'(x)>0。
所以g(x)在(0,x0)上是增函数,在(x0,1)上是减函数,在(1,+∞)上是增函数。
因为g(1)=<0,g(2)=e2-2+ln 2>0,所以g(x)在(1,+∞)内有且只有一个零点。
综上所述,g(x)有且只有一个零点。
①当a≤0 时,f'(x)>0,f(x)单调递增,所以f(x)的单调递增区间为(0,+∞),无单调递减区间。
综上可得,当a>0时,f(x)的单调递增区间为,单调递减区间为;
当a≤0时,f(x)的单调递增区间为(0,+∞),无单调递减区间。
(3)由(2)可得,当a≤0时,f(x)单调递增,则f(x)至多一个零点。
若-lna-1<0,即a>,则方程f(x)=0无解。
若-lna-1>0,即0<a<,则方程f(x)=0有两个不等解。
由于x>0,不妨令x1>x2>0,则有lnx1=ax1,lnx2=ax2,所以lnx1+lnx2=a(x1+x2),lnx1-lnx2=a(x1-x2),所以a=。
因为t>1,所以g'(t)>0 恒成立,所以g(t)在(1,+∞)上单调递增。
54.(1)由题可知f(x)的定义域为(-1,+∞),f'(x)=-a。
若a≤0,则f'(x)>0 恒成立,所以f(x)在(-1,+∞)上单调递增,且f(0)=0,所以f(x)存在唯一零点。
当a∈(0,1)时,h'(a)<0,h(a)单调递减;当a∈(1,+∞)时,h'(a)>0,h(a)单调递增。
所以h(a)≥h(1)=0,故当a-1-lna=0时,a=1。
综上可得,当f(x)存在唯一零点时,实数a的取值范围为a≤0或a=1。
(2)由(1)知,当a=1时,f(x)=ln(x+1)-x在(0,+∞)上单调递减,所以f(x)<f(0)=0,即ln(x+1)<x在(0,+∞)上恒成立。
令x=3-n,n=1,2,3,…,则ln(1+3-n)<3-n,所以ln[(1+3-1)(1+3-2)(1+3-3)…(1+3-n)]=ln(1+3-1)+ln(1+3-2)+ln(1+3-3)+…+ln(1+3-n)<3-1+3-2+3-3+…+3-n=。
所以ln[(1+3-1)(1+3-2)(1+3-3)…(1+3-n)]<。
所以当n∈N*时,(1+3-1)(1+3-2)(1+3-3)…(1+3-n)<。

