2023 年高考新课标Ⅱ卷数学第22 题的解法探究及溯本探源

陕西省榆林市吴堡中学 (718200) 郭蒙

1 试题呈现

题目1(2023 年高考新课标Ⅱ卷第22 题)

(1) 证明: 当0＜x＜1 时,x-x2＜sinx＜x.

(2) 已知函数f(x) = cosax-ln(1-x2),若x= 0 是f(x)的极大值点,求a的取值范围.

此题是2018 年全国卷Ⅲ理科数学第21 题的姊妹题,该题目是:

溯源1(2018 年全国卷Ⅲ理科第21 题) 已知函数f(x)=(2+x+ax2)ln(x+1)-2x,(1)略;

(2)若x=0 是f(x)的极大值点,求a的取值围.

2018 年导数题号称当年最难的一道压轴题,今年这道高考题,立意更新颖,内容更丰富,考察函数单调性、极值等相关问题,将对数函数、三角函数、函数奇偶性与单调性等紧密联系在一起,全面渗透了逻辑推理、数学运算等核心素养,体现了基础性、综合性、创新性和应用性的考察要求,发挥数学科目在人才选拔中的重要作用,是全面发展的素质教育,育人理念,是高考从知识立意、能力立意到素质立意的转变,故而是一道非常精彩的压轴题,难度较大,创新性极高,具有很强的选拔性[1].

2 解法探究

2.1 第(1)问的证明

证明设g(x) = sinx-(x-x2) = sinx-x+x2,x∈(0,1),g′(x) = cosx-1+2x,g′′(x) = 2-sinx＞0,因此g′(x) 在(0,1) 上单调递增,g′(x)＞g′(0) = 0, 故g(x) 在(0,1)上单调递增,g(x)＞g(0) = 0, 即x-x2＜sinx. 设m(x) =x-sinx,x∈(0,1), 因为m′(x) = 1-cosx≥0,所以m(x) 在(0,1) 上单调递增,m(x)＞m(0) = 0, 因此sinx＜x,综上,原不等式成立.

评注第一问常规题型,突出对基础知识和基本性质的考察要求,第一问的结果为第二问作铺垫,可以降低第二问的难度.

2.2 第(1)问的解答

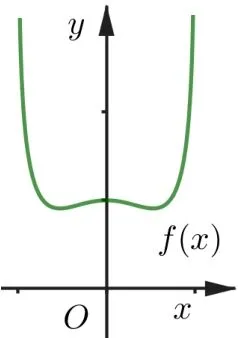
当x∈(0,x0)时,h(x)＜0,f′(x)＜0,因此f(x)在(0,x0)上单调递减,因为f(x)为偶函数,所以f(x)在(-x0,0)上单调递增,符合题意,图象如右图所示.

(2)当a=0 时,

f(x)=1-ln(1-x2)≥1-ln 1=1=f(0),不满足题意,舍去.

评注由于f(x)为偶函数,只需讨论f(x)在(0,1)上的情况,又cos(-ax)=cosax,只需讨论a≥0 的情形,利用第(1)问结论,将三角函数放缩为一次和二次函数,降低了试题的难度,由于函数的极值点是函数的局部性质,因此只需考虑函数在x=0 附近的情况.

其中o((x-x0)n)为(x-x0)n的高阶无穷小量,此公式又称为带有佩亚诺型余项的泰勒公式. 泰勒公式的作用在于任意一个可导函数都可用多项式函数来逼近,为解决一些复杂函数问题带来新的视角,也为高考导数压轴题提供命题的立意与背景,利用高观点对其进行溯本探源是很有必要的. 当x0= 0 时的泰勒公式称为麦克劳林公式, 常见的泰勒公式有:

极值的第二充分条件[3]设若函数f(x) 在点x0的某邻域U(x0;δ) 内一阶可导, 在x=x0处二阶可导, 且f′(x0) = 0,f′′(x0)／= 0. (i)若f′′(x0)＜0, 则函数f(x)在x0取得极大值;(ii)若f′′(x0)＞0,则函数f(x)在x0取得极小值.

极值的第三充分条件[3]设若函数f(x)在点x0的某邻域内存在直到n-1 阶的导函数,在x=x0处n阶可导,且f(k)(x0)=0,(k=0,1,2,···,n-1),f(n)(x0)／=0,则(i)当n为偶数时,函数f(x)在x0取得极值,且当f(n)(x0)＜0 时取极大值,f(n)(x0)＞0 时取极小值;(ii)当n为奇数时,函数f(x)在x0处不取极值.

评注利用大学数学分析知识,很容易得到参数a的范围,可以利用此法来探路,再利用分类讨论完美解答此题,为学生高等数学的学习做铺垫.

3 结语

今年这道高考题,考察学生对极值点概念的理解,彰显了试题综合性的要求,是一道非常精彩的压轴题,难度较大,创新性极高,发挥了数学科目在高考中的选拔功能,我们用8种方法探究问题,激发了学生的发散思维和创新精神. 用高观点来指导高中数学的教学是很有必要的,可以将问题化难为易,变得简单明了,很多问题只有在高观点下才能得到更深刻的理解,只有厘清高等数学与初等数学的结合点,深入剖析高考热点问题,才能准确把握高考命题的新方向[4]. 在高三一轮复习时,老师们应重视基础知识,强化基础知识的落实,为二轮复习做好铺垫,重视通性通法,重视知识的形成过程,淡化技巧,做完题要反思,体会出题人的意图,明确考察的知识与能力,落实数学学科核心素养,重视导数与三角函数、数列等的多元融合,适当渗透高观点去探究问题的本质,开阔解题思路,提高学生分析问题、解决问题的能力,进一步提升学生的数学学科素养,希望本文对读者的学习有一定的启发作用.