遵循概念形成路径 提升问题解决能力
张银德 李娟

解决行程问题的关键是理解速度模型。这对四年级学生来说有一定的难度。如何通过《速度、时间和路程》一课的教学,让学生更好地理解速度概念,建构速度模型,获得变式应用能力,而非仅仅学会套用相关公式呢?
一、教学内容的学理分析
《速度、时间和路程》是人教版数学四年级上册第四单元《三位数乘两位数》的内容。整个单元有5个例题和2个练习,《教师教学用书》建议用6课时教学。从课时分配来看,《速度、时间和路程》原则上只有1课时;从教材编排来看,作为与乘法相关的常见数量关系,“速度、时间和路程”与“单价、数量和总价”的地位看似相同、实则不同,对于“单价、数量和总价”,学生在生活中常常见到,有经验、有感受,而对于“速度、时间和路程”,学生是说不清道不明的;从数量关系来看,“单价、数量和总价”与个数有关,“速度、时间和路程”与物理量有关,后者的理解难度更大。
对于本课的教学,《教师教学用书》建议“结合生活实际理解概念内涵”,“结合概念意义,自主建构数量关系”;《义务教育数学课程标准(2022年版)》提出,“感悟模型中量纲(即单位)的意义,提升问题解决的能力”。笔者认为,理解速度概念和学会解决问题的方法是学生问题解决能力提升的“一体两面”,二者相辅相成、缺一不可。要想提升学生的问题解决能力,教师就要遵循概念的形成路径,引导学生把握速度概念的本质,以灵活解决不同变式的实际问题。
二、教学实施的实践路径
1.唤醒已有认知,初识概念
学生学习速度概念之前往往存在仅根据行进终点的远近判断速度快慢的认知误区。基于此,教师可以结合学生的生活经验,创设“比快慢”的问题情境,引导学生从“仅根据行进终点的远近判断速度快慢”的初始经验展开学习,并观测学生的实际认知水平,动态调整后续教学,逐步引导学生纠正、完善、深化对速度概念的认知。
课堂上,笔者出示如下行程图,引导学生依次思考以下4个问题。
①通过看图,你能判定小牛和小熊谁跑得快吗?②如果小牛7分钟跑了700米,小熊7分钟跑了900米,你能判定小牛和小熊谁跑得快吗?③如果小牛跑350米用5分钟,小熊跑350米用7分钟,你能判定小牛和小熊谁跑得快吗?④如果小牛5分钟跑了300米,小熊10分钟跑了600米,你能判定小牛和小熊谁跑得快吗?这4个问题紧扣主题、逐层深入:问题①仅有“路程”一个量,问题②有“时间、路程”两个量且“时间”相同,问题③有“时间、路程”两个量且“路程”相同,问题④有“时间、路程”两个量且均成倍数关系。这样的问题情境符合学生的认知基础,能唤醒学生的已有经验,使学生通过对比、辨析,初步感知速度概念,认识到比快慢的前提是要“对齐”一个量,即固定时间或固定路程。同时,在笔者的点拨下,学生还意识到这与度量中的零刻度对齐、计算中的数位对齐道理相通。
解决以上问题的过程中,笔者重点关注的不是学生获得问题本身的结果,而是学生思维素养的提升。想明白比较快慢的道理是学生后续解决稍复杂行程问题的基础。
2.复杂问题驱动,建立标准
维果茨基认为,概念的学习有“迁移、给概念下定义、在新情境中解决问题”三个困难。要深化学生对速度的认知,教师还要创设更复杂的问题情境,将学生的思维引向深入。
课堂上,小牛、小熊的故事还在继续。此处,笔者引入了一个新朋友——小象,创设了如下图所示的稍复杂的问题情境。
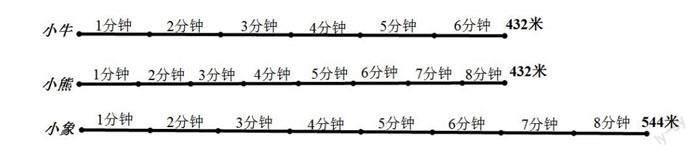
怎样用数学的方式表达问题情境中的数学信息是学生首先要解決的问题,也是学生提升问题解决能力的关键。笔者引导学生先根据路程画出3条线段,再分别根据时间把线段平均分段,并标注相关数据(如下图)。
从线段图中可以看出,小牛和小熊的路程相同、时间不同,小熊和小象的时间相同、路程不同。笔者引导学生通过“对齐”一个量展开分析,解决“小象和小熊”“小牛和小熊”谁跑得快的问题,以强化学生对速度的认知。随着“小牛比小熊跑得快”“小象比小熊跑得快”结论的揭晓,新的问题“小牛和小象谁跑得快”产生了。面对新问题,学生的原有认知既是学习支架又可能成为学习障碍。基于此,笔者帮助学生解构旧概念,建立更完善的评判速度快慢的标准。
具体如何做呢?笔者引导学生观察表示时间的数字(6和8)特征,想办法“对齐”时间这个量。学生提出可以比较24分钟内小熊和小象所跑的路程:小象8分钟跑了544米,24分钟应跑“544×3=1632”米;小牛6分钟跑了432米,24分钟应跑“432×4=1728”米。这说明小牛比小象跑得快。
教学设计从最初只考虑路程这一个量过渡到对比相同时间内的路程,学生通过稍复杂问题的解决,加深了对速度、时间和路程之间关系的理解。
3.提升价值定位,提炼模型
一般地,我们认为这节课是问题解决的课型,为什么笔者的教学设计更倾向于概念教学呢?因为速度相关问题的解决过程就是学生形成速度概念的过程。学生需要在解决简单问题的过程中初步感知概念,然后在解决稍复杂问题的过程中深入理解概念、建立思考模式,再在变式问题的对比分析中提炼基本模型,形成计算公式。这是速度概念形成的基本路径。
在学生学会分析、解决稍复杂问题后,笔者呈现变式问题:小猫4分钟跑了20米,小狗7分钟跑了56米,小猫、小狗谁跑得快?笔者引导学生观察之前小牛、小熊、小象跑步情况的线段图,学生发现“6分钟”是由6个1分钟累加起来的,“8分钟”是由8个1分钟累加起来的。笔者进一步引导学生尝试比较单位时间内的路程,即比较小猫和小狗1分钟所跑路程的长短,以此判定速度快慢。小猫4分钟跑了20米,平均每分钟跑了“20÷4=5”米;小狗7分钟跑了56米,平均每分钟跑了“56÷7=8”米。所以小狗比小猫跑得快。这个问题的解决基于“每分钟跑5米”与“每分钟跑8米”的对比。
从最初只考虑路程这一个量到对比相同时间内的路程,再到对比单位时间内的路程,学生采用归纳的学习方式将速度概念的本质提炼出来,理解了“速度是单位时间内走过的路程”的真正含义,建构了“速度=路程÷时间”的模型,并由此变式得出“路程=速度×时间”“时间=路程÷速度”的模型。
后续,笔者引导学生通过画一画的方式表示“5米/分”。在学生只画1段线段表示1分钟走5米的情况下,笔者引导学生画2段、标注“2分钟走10米”来表示,画3段、标注“3分钟走15米”来表示,使学生深度体会到“速度是单位时间内走过的路程”。
(作者单位:张银德,枣阳市王城镇中心学校;李娟,枣阳市教学研究室)
责任编辑 刘佳

