基于强化学习的改进NSGA-II 算法的城市快速路入口匝道控制

陈 娟, 郭 琦

(上海大学悉尼工商学院, 上海 201800)

近年来, 随着我国社会经济的飞速发展, 城市居民人口逐年增加, 汽车保有量也在不断攀升, 而交通基础设施的供应却相对滞后, 由此产生了严重的城市交通拥堵问题. 交通拥堵使得快速路的利用率不高, 目前上海市快速路瓶颈点常发性拥挤占整个系统拥挤的50% 以上[1].交通拥堵还会进一步引发环境污染问题, 延长个人出行时间, 造成一定程度的经济损失. 因此,采取控制方法提高路网通行效率, 缓解交通拥堵, 具有非常重要的现实意义.

研究表明, 城市快速路普遍存在着拥挤和堵塞现象, 而瓶颈点则是快速路能否运行畅通的关键. 匝道入口、匝道出口和出口下游连接区域是快速路的瓶颈区域, 是拥堵现象的高发区,匝道汇入区也是常发性瓶颈中的一种[2]. 在快速路已经建成的现有条件下, 由于经济和环境原因, 通过增建基础设施的传统举措往往在短期内无法实现. 通过改善匝道汇入方法以缓解交通拥堵已成为最具现实意义和研究意义的举措. 快速路交通控制研究经验也表明, 匝道控制是达到缓解交通拥堵这一目的最直接和最有效的控制方法.

已有的对快速路匝道信号控制方法的研究主要分为静态控制、单点动态控制和动态协调控制. 静态控制是根据历史数据制定不同时段内各个匝道的协调控制策略, 并预置在控制机中, 但不会针对实时检测信息做出响应. 典型方法有线性规划[3], 具有简单易行, 但灵活性较差的特点. 单点动态控制的基本目的是解决单个匝道的交通拥挤问题, 控制范围为某一处匝道,利用匝道及其相邻路段的实时检测或预测数据代替历史数据作为控制决策的基础. 经典方法有ALINEA 方法[4], 具有控制灵活性较大, 但仅局限于单个匝道控制的特点. 动态协调控制兼具协调控制与动态控制的特征, 控制范围为高速道路系统所有或局部区域部分匝道, 利用实时检测或预测数据代替历史数据作为控制决策的基础. 动态协调控制分为系统最优协调控制、状态调节器控制和启发式协调控制[5], 能够控制多个匝道, 但在实际应用中难以实现整个路网的系统最优.

本工作结合强化学习方法和非支配排序遗传算法(non-dominated sorting genetic algorithm II, NSGA-II) 解决城市快速路入口匝道控制问题, 将基于竞争结构的深度Q 网络(dueling deep Q network, Dueling DQN)、深度循环Q 网络(deep recurrent Q network,DRQN) 和NSGA-II 算法结合用于匝道控制, 并与无控制情况和NSGA-II 算法进行了比较.

本工作的主要贡献如下: ①基于交通流METANET 模型、宏观尾气排放和燃油消耗VTMacro 模型, 考虑最小化总花费时间(total time spent, TTS)、总尾气排放(total emissions,TE)、总燃油消耗(total fuel consumption, TF), 将Dueling DRQN-NSGA-II 算法用于城市快速路入口匝道控制问题; ②提出的Dueling DRQN-NSGA-II 算法, 首次将NSGA-II 算法和基于强化学习的Dueling DQN、DRQN 算法相结合, 有效提高了NSGA-II 算法的多样性; ③与无控制情况、Q 学习-NSGA-II (Q-NSGA-II)、深度Q 网络-NSGA-II (DQN-NSGA-II)、基于竞争结构的深度Q 网络-NSGA-II (Dueling DQN-NSGA-II)、深度循环Q 网络-NSGA-II(DRQN-NSGA-II) 算法以及NSGA-II 算法比较, 本工作提出的Dueling DRQN-NSGA-II 算法控制效果表现最优. 实验结果表明: Dueling DRQN-NSGA-II 能有效改善路网通行效率、缓解环境污染、减少能源损耗; 相对于无控制情况, TTS 减少了16.14%, TE 减少了9.56%, TF得到了43.49% 的改善.

1 文献回顾

匝道控制是解决城市快速路拥堵问题的重要措施, 通过对匝道汇入车辆的管理和调节, 能够确保快速路的高效运行.

由于快速路环境复杂, 若要更加全面地考虑快速路的效率, 达到更好的控制效果, 就无法避免多个控制目标的存在. 由于有些目标之间存在冲突, 因此需要考虑多目标控制方法来协调控制多个目标, 以取得多个目标之间的最优解. Meng 等[6]指出NSGA-II 算法设立的目标是不仅使总系统延迟最小化, 而且使与路段相关的公平指数最大化. 该算法能够寻求帕累托(Pareto) 最优解. Maldonado 等[7]提出了一种多目标NSGA-II 算法, 可显著提高交通流量. Tam´as 等[8]研究中的标准H∞控制能够通过缩短车辆所花费的总时间来优化交通性能,减小CO2的排放因子. Xie 等[9]考虑了匝道控制和可变限速策略, 提出了多目标粒子群优化算法. 该算法有效提高了路网的移动性, 降低了车辆碰撞风险, 减少了碳排放. Yu 等[10]针对多个匝道的高速公路考虑了不同车型, 提出了可变限速策略, 并使用遗传算法求解该问题. 该算法能有效提高路网运行效率、减少排放. Chen 等[11]提出了一种基于聚类预测的动态多目标优化算法, 能有效缓解交通拥堵, 减少尾气排放与能源消耗, 但运算效率较低. 陈娟等[12]考虑到快速路的多种车型, 提出了模糊非支配排序遗传算法, 有效改善了环境和道路通行效率.Kotsialos[13]将协同运行模式策略设计为最优控制问题, 并使用随机搜索算法求解静态问题.结果表明, 所采用的算法是合理的, 可以减少TTS, 减少路网的总排放, 但需要大量计算时间才能收敛到足够质量的解.

在仅考虑单个匝道的情况下, Davarynejad 等[14]提出了一种基于Q 学习的密度控制方法.但该方法未与其他匝道控制方法进行比较, 不能判断其优劣. Veljanovska 等[15]的研究虽然没有考虑实际场景, 但方法简单, 不需要对交通参数进行预测. 典型的强化学习方法考虑使用离散状态表示, 但这会导致复杂问题的缓慢收敛, Rezaee 等[16]采取k 近邻时域差分来表示连续状态空间. 但该研究仅考虑了单匝道控制方法, 没有协调多智能体情况, 无法达到整体的性能最优. Lu 等[17]的研究考虑了交通事故, 所提出的间接强化学习方法在大多数场景下性能更优,且学习速度更快. Fares 等[18]设计了一种基于密度控制智能体的强化学习方法, 平衡了快速路的需求和容量. Ivanjko 等[19]使用VISSIM 作为仿真软件, 将最大入口匝道队列长度限制在一定上限, 对Q 学习进行调参后, 与无控制和未调参情况比较, 匝道控制效果更好. 段荟等[20]结合了协同运输管理(collaborative transportation management, CTM) 模型和Q 学习对匝道汇入率进行调节. 但该研究是在假设驾驶员对限速的遵从度为100% 的基础上进行的, 没有考虑不同驾驶员对限速的实际遵从情况, 没有探讨不同的参数选取及函数设置下策略的学习控制效果. Wu 等[21]提出的基于深度演员-评论家的差分变速限制策略可有效提高快速路通行量, 减少排放, 增强安全性. 由于路网上的交通摄像机可以覆盖更大的区域, 提供更详细的交通信息, Liu 等[22]提出了一种深度强化学习方法, 以探索交通视频数据在提高匝道控制效率方面的潜力. 该方法能有效缩短主线行驶时间和入口匝道车辆排队时间, 并增加了流区下游的通流量.

2 问题描述

在研究快速路交通控制问题时, 通常使用TTS 来衡量路网通行效率. 此外, 本工作还考虑了路网中车辆通行对环境和能源消耗的影响, 将TE 和TF 设置为性能指标. TE 和TF 主要参考了Zegeye 等[23]研究中的METANET 模型和VT-Macro 模型.

2.1 METANET 模型和VT-Macro 模型

2.1.1 宏观交通流METANET 模型

METANET 模型是由Papageorgiou 等[24]于1990 年在对巴黎南部某地区进行交通模型构建及控制时提出的. 该模型是一种在时间和空间上都离散的二阶模型. 它将快速路的连续路段离散化分成若干路段, 流量参数可能因路段的不同而有所差异. 划分的路段数越多, 每条路段的平均长度就越短, 就能更加准确地表示路段间交通流参数的互异性.

(1) 车辆守恒方程描述的是流量与密度的关系, 即

式中:k表示第k个时间间隔;i表示第i个路段;T(h)表示离散时间间隔;ρi(k)(veh/(km·lane))表示第k个时间间隔路段i的车辆密度;Li(km) 表示第i个路段的长度;λi表示第i个路段的车道数;qi(k) (veh/h) 表示第k个时间间隔路段i的平均车流量.

(2) 流量密度方程描述的是每路段的驶出交通量等于车流密度、平均速度以及车道数的乘积这一基本关系, 即

式中,vi(k) (km/h) 表示第k个时间间隔路段i的车辆平均速度.

(3) 动态速度密度方程为

式中:τ、υ、κ和δ表示路网交通特性的相关参数, 依次为时间相关常数、期望常数、修正常数和匝道汇入影响系数;V(ρi(k)) (km/h) 表示驾驶员的平均期望速度, 也称为稳态速度;qo(k)(veh/h) 表示第k个时间间隔从入口匝道o处汇入主路的平均车流量.

(4) 稳态速度密度方程描述的是稳态速度与路段密度之间的关系, 即

式中:αi表示模型参数;vf,i(km/h) 表示快速路路段i的自由流速度;ρcr,i(veh/(km·lane))表示路段i的临界密度.

(5) 起点排队模型主要用于描述起始路段(主路起始路段或入口匝道) 处的车辆排队情况.起点排队模型包括匝道排队模型以及匝道汇入主线模型. 匝道排队长度表达式为

式中:do(k) (veh/h) 表示入口匝道o处第k个时间间隔的平均到达车流量;wo(k) (veh) 表示入口匝道o处在第k个时间间隔的车辆排队长度.

上述匝道排队长度中的qo(k) 可由以下式子求得, 即

式中:ro(k)∈[0,1] 表示入口匝道汇入率, 若ro(k) = 1, 则表示没有实施匝道控制, 若ro(k) = 0, 则表示不允许车辆从匝道汇入主路;Qo(veh/h) 表示入口匝道饱和流量;ρmax(veh/(km·lane)) 表示主路路段的最大车流密度; 最大输出量(k) (veh/h) 是由入口匝道流量需求(k) (veh/h) 和相连快速路路段的最大可用容量(k) (veh/h) 决定的.

2.1.2 宏观尾气排放和燃油消耗VT-Macro 模型

为了权衡模型的预测精度与计算时间, 可以采用VT-Macro 模型来计算尾气排放量与燃油消耗量. VT-Macro 模型是结合METANET 模型和VT-Micro 模型产生的, 能够动态反映整体汽车尾气排放量和燃油消耗量[23]. 首先, 基于METANET 模型的平均速度等交通状态给出加速度算式. 其次, 构建尾气排放量和油耗量与车辆平均速度、平均加速度的回归方程模型.

VT-Macro 模型的第k个时间间隔路段i的车辆时间加速度(k) (km/h2) 表示为

对应的快速路路段i上的车辆数(k) (veh) 为

第k个时间间隔从路段i到路段i+1 的车辆时空加速度(k) (km/h2) 表示为

对应的从路段i到路段i+1 的车辆数(k) (veh) 为

除在同一道路连续路段上行驶车辆的时空加速度外, 入口匝道处的平均时空加速度aon,o(k) (km/h2) 和对应的车辆数non,o(k) (veh) 分别为

式中,qon,o(k) (veh/h) 为实际入口匝道流量qo(k).

综合上述车辆平均速度、加速度和车辆数, 可以得到宏观车辆尾气排放和燃油消耗的VT-Macro 模型. 以时间加速度为例, 第k个时间间隔路段i的车辆燃油消耗或尾气排放量为

式中:y ∈{CO,HC,NOx,FC}, 其中CO、HC、NOx为常见的尾气污染物, FC 为燃油消耗;Py表示参数矩阵[23]. 其余两种加速度的指标算式(k)、Jy,on,o(k) 与上式类似. 快速路路段i在k个时间间隔的车辆燃油消耗或尾气排放量为

式中: on 表示入口匝道;(k) 表示主路在第k个时间间隔路段i上正常行驶产生的尾气排放或燃油消耗量;(k) 表示主路在第k个时间间隔路段i上因停车而产生的尾气排放或燃油消耗量;Jy,o,on(k) 表示在第k个时间间隔入口匝道o上产生的尾气排放或燃油消耗量.

2.2 性能指标

2.2.1 总花费时间

TTS 主要包括路网中车辆的总行程时间(total travel time, TTT)与入口匝道车辆排队的总等待时间(total waiting time, TWT). TTS 最小化是指在路网中花费的时间最小化. TTS(veh·h) 具体计算方式表示为

式中,wo,i(k)(veh) 表示第k个时间间隔路段i上第o个入口匝道的排队长度.

2.2.2 总尾气排放与总燃油消耗

TE 是指一定时间内通过既定路网的所有车辆产生的尾气量总和. TF 是指一定时间内通过既定路网的所有车辆消耗的燃油总量. 根据VT-Macro 模型, 本工作主要关注的尾气为CO、HC、NOx. 各类尾气的TE (kg) 与TF (L) 的计算公式为

为了环保和低耗, 因此设置最小化尾气排放量和燃油消耗量. 由于TE 和TF 是两种不同类型与量纲的指标, 不能直接相加, 本工作先将其标准化处理后再相加, 即将式(21) 转变为

式中:JCO、JHC、JNOx三者之和表示TE;JFC表示TF;Jnc,emission(kg) 和Jnc,FC(L) 分别表示无控制情况下的路网尾气排放总量和燃油消耗总量, 均可以通过后续的仿真实验得到具体的数值.

图1 为本工作算法模型的交互框架. 本算法由Dueling DRQN 和NSGA-II 组成. Dueling DRQN 从NSGA-II 中获得解间距值, 得到状态后由Dueling DRQN 将动作种群比例参数输出给NSGA-II. Dueling DRQN-NSGA-II 将METANET 模型和VT-Macro 模型[23]转化成最小化TTS、TE 和TF 问题, 之后再将匝道控制率给到METANET 模型和VT-Macro 模型,使得匝道车辆能够汇入主路.

图1 算法模型交互框架Fig.1 Algorithm model interaction framework

本工作对多目标问题适应度函数设计如下: 根据对TTS、TE 和TF 这3 个性能指标的描述, 尽可能地减小TTS、TE 和TF. 因此本工作采用如下的NSGA-II 算法的适应度函数:

式中:J1(k)、J2(k) 分别表示第k个时间间隔的TTS、TE 和TF;Jnc,1(k) (veh·h) 表示无控制情况下的TTS;ω1,ω2表示各目标的重要程度, 分别为0.5、0.5.

3 基于强化学习的改进NSGA-II 算法Dueling DRQN-NSGA-II

3.1 强化学习问题描述

本工作将NSGA-II 中的种群视为智能体, 最终目标是种群比例参数的学习. 智能体通过感知种群多样性变化来控制种群比例参数, 进而控制种群进化方向. 当解间距相较于初始种群减小时, 说明种群比例设置是合理的.

3.1.1 状态描述

间距S反映了算法获得帕累托前沿(Pareto front, PF) 的均匀性. 一般而言, 间距越小,说明算法得到的最优解集在目标空间越接近等间距分布.

设算法搜索到的具有Pareto 性的前沿解的个数为|A|, 则定义解间距指标Sp为

式中:其中表示di的平均值,M表示目标函数的个数.Sp越小说明得到解的分布越均匀, 种群多样性越好.

状态空间由种群解间距值变化划分为9 个, 具体定义如表1 所示, 其中分别表示初始种群1 和初始种群2 的解间距,分别表示第t代种群1 和种群2 的解间距.

表1 状态定义及意义Table 1 States definition and significance

3.1.2 动作描述

强化学习Agent 的动作是对种群比例参数的调整, 包含增加、不变、减少3 种, 具体计算公式为

式中,a(t)、a(t-1) 分别表示第t和t-1 代种群的分割比例参数.

3.1.3 奖赏函数描述

依据解间距变化决定Agent 的奖赏, 目标是学习最优的比例参数β(t).、分别表示第i个种群第t代的解间距和初始种群i的解间距, 具体计算公式为

3.2 基于竞争结构和深度循环的Q 网络Dueling DRQN

本工作结合Dueling DQN[25]和DRQN[26], 提出了改进DQN 算法, 称为基于竞争结构和深度循环的Q 网络(Dueling DRQN) 算法.

Dueling DQN 将原有的DQN 算法的网络输出分成了两部分——即值函数V和优势函数A, 在数学上表示为

式中,α、β表示两个全连接层网络的参数.

Dueling DRQN 与DQN 算法的不同之处在于, 将DQN 中第1 个全连接层的部件替换成了长短期记忆单元(long short-term memory, LSTM), 并且把Q值更新分开成两个部分: 一个是值函数; 一个是独立于状态的动作优势函数.

Dueling DRQN 算法伪代码的具体表示如下.

3.3 Dueling DRQN-NSGA-II 强化学习问题描述

本工作提出的Dueling DRQN-NSGA-II 算法主要包括3 个部分: 基于竞争结构的深度Q网络(Dueling DQN)、深度循环Q 网络(DRQN) 以及基于NSGA-II 的主算法. 算法流程如图2 所示.

图2 基于强化学习的改进NSGA-II 算法流程图Fig.2 Flow chart of the improved NSGA-II algorithm based on reinforcement learning

本工作提出的Dueling DRQN-NSGA-II 算法步骤如下.

步骤1 初始化参数, 设置算法相关参数: 种群迭代次数G; 种群规模N; 交叉概率Pc; 变异概率Pm; 初始化回放记忆D; 可容纳数据条数N; 学习率α以及折扣率γ; 利用随机权重θ来初始化动作行为值函数Q.

步骤2 产生初始种群, 计算初始种群解间距值.

步骤3 对种群进行快速非支配排序和拥挤度计算.

步骤4 初始按照比例0.5 拆分种群, 后续按照动作拆分种群, 通过双种群进化策略获得新一代种群.

步骤5 判断是否达到最大迭代次数. 如果是, 则结束迭代; 否则, 执行步骤6. 计算种群的解间距, 获得状态s.

步骤6 计算奖励值R, 根据3.2 节的Dueling DRQN 算法更新Q值表.

步骤7 采用ε-贪心策略选择动作a, 更新种群比例参数, 转到步骤3.

4 实 验

4.1 实验设置

本工作建立的测试单入口匝道路网如图3 所示. 该路网的快速路主路包括3 个车道, 总长为1 500 m. 将该路网划分为3 个路段, 每条路段长为500 m. 在路段2 处有一个入口匝道, 匝道为单车道. 本工作采用METANET 模型和VT-Macro 模型, 分别模拟路网的交通行为及计算尾气排放量与燃油消耗量, 模型参数参考文献[27]. 主路和入口匝道的交通需求量如图4 所示, 通过模拟一个早高峰现象, 设置主路及入口匝道的通行能力分别为2 000 和1 500 veh/(km·lane).

图3 单匝道快速路网Fig.3 Freeway network with an on-ramp

图4 主路和入口匝道的交通需求量Fig.4 Traffic demands of the mainline and the on-ramp

4.2 实验结果

4.2.1 算法参数设置

为了验证本算法的有效性, 首先在Dueling DRQN-NSGA-II 不同超参数下测试, 选择最优超参数.

在其他超参数都相同的条件下, 分别测试了折扣因子GAMMA 值为0.90、0.95、0.99, 以及学习率(learning rate, LR) 为0.01、0.001 和0.000 1 时的收敛情况, 并以解间距作为训练收敛的评估指标. 图5 为不同超参数下的解间距值图. 可以看到: 折扣因子和学习率的不同均能影响算法的收敛; 很显然, 当折扣因子为0.95, 学习率为0.001 时, 种群的解间距能够快速降低并保持在较小的范围内, 说明此时得到的解更加均匀.

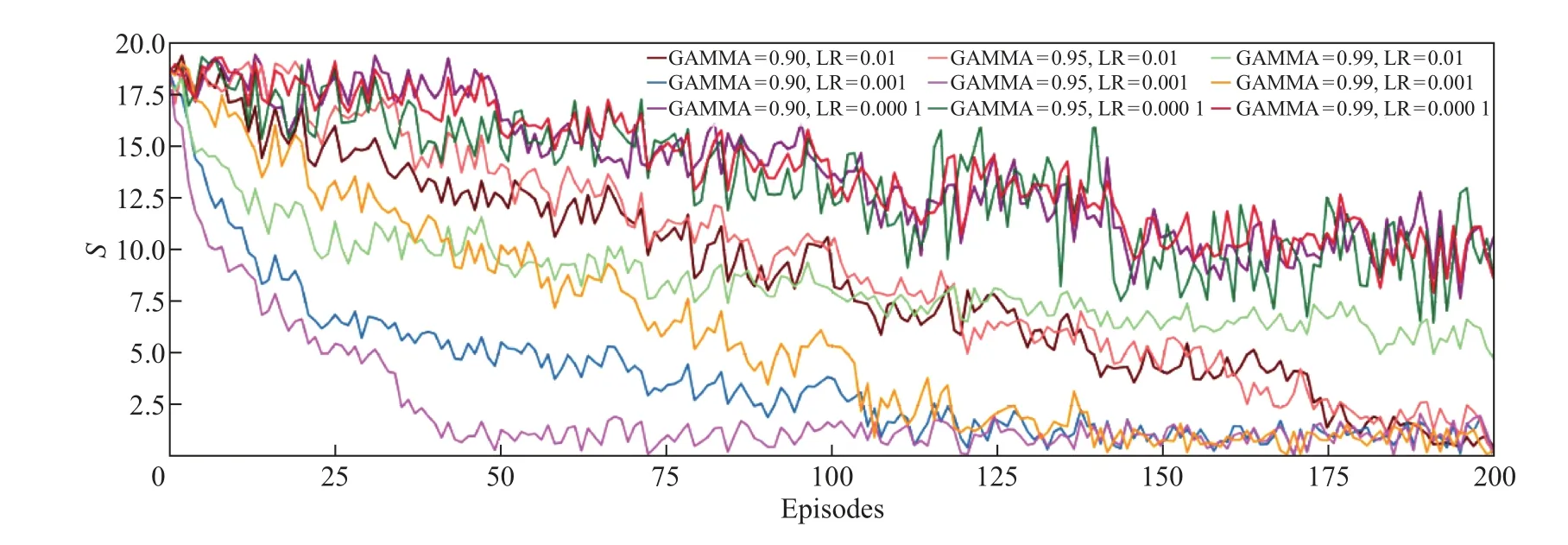
图5 不同超参数下的解间距值Fig.5 Solution spacing values under different hyperparameters

此外, 为了验证Dueling DRQN-NSGA-II 算法改进部分的有效性, 以TTS、TE、TF 目标函数之和为适应度值, 分别采用NSGA-II、Q-NSGA-II、DQN-NSGA-II、Dueling DQNNSGA-II、DRQN-NSGA-II、Dueling DRQN-NSGA-II 算法进行求解, 得到如图6 所示的算法收敛性对比图.

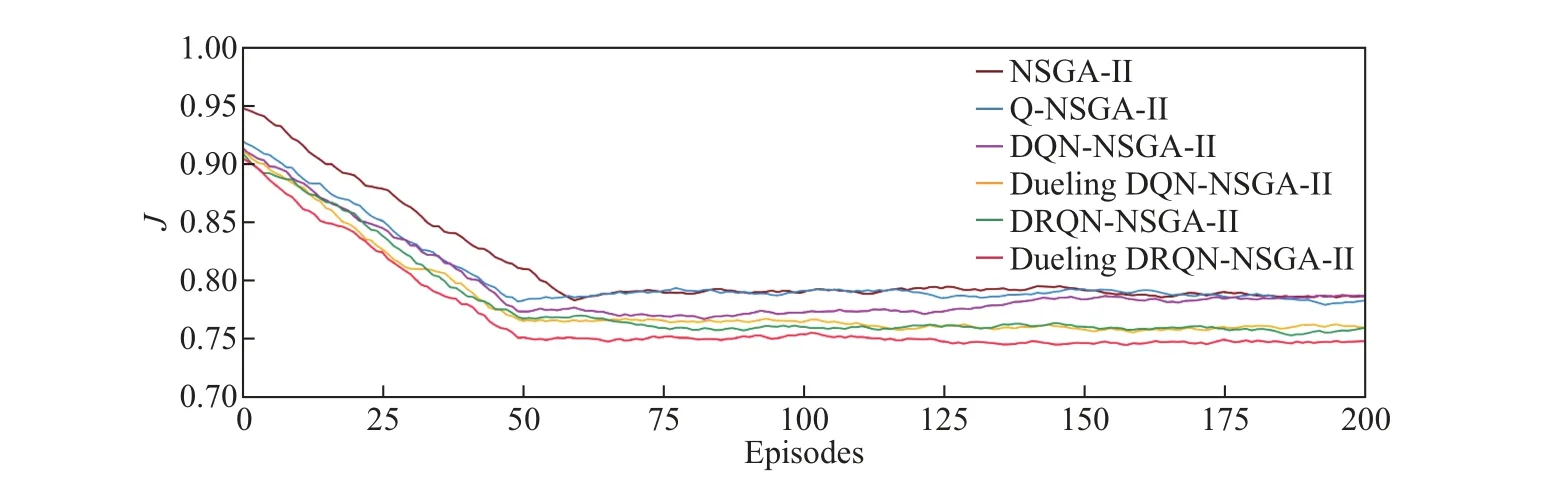
图6 算法收敛性对比Fig.6 Comparisons of algorithm convergence

由图6 收敛曲线的对比分析可知, 将强化学习方法与NSGA-II 算法结合后, 可提升算法的收敛速度; 使用本工作提出的Dueling DRQN-NSGA-II 算法, 可使收敛速度更快, 种群适应度值更优, 并由此证明了Dueling DRQN-NSGA-II 算法可以改善NSGA-II 算法的收敛性.

4.2.2 实验结果分析

为了便于实施仿真和分析仿真结果, 本工作假设仿真路网中驾驶员对限速的遵守率为100%, 即a= 0; 仿真时长取3 h; 采样周期取10 s; 控制周期取1 min. 本工作从路网主路的交通状态及匝道排队, 分别对无控制、NSGA-II 控制、Q-NSGA-II 控制、DQN-NSGA-II 控制、Dueling DQN-NSGA-II 控制、DRQN-NSGA-II 控制和Dueling DRQN-NSGA-II 控制这7 种控制算法进行对比分析, 最后根据仿真结果对这7 种控制算法的路网整体性能指标进行分析说明.

(1) 各控制算法下的交通状态分析.

图7 为无控制、NSGA-II 控制、Q-NSGA-II 控制、DQN-NSGA-II 控制、Dueling DQNNSGA-II 控制、DRQN-NSGA-II 控制和Dueling DRQN-NSGA-II 控制这7 种控制算法下路段2 的交通状态变量图. 图7(a) 为这7 种控制算法下路段2 的车流量. 可以看出: 相对于无控制情况, 另外6 种控制算法在前1 小时仿真时间内能够使路网中有更多的车辆通行. 图7(b)为这7 种控制算法下路段2 的车辆密度. 可以看出: 无控制情况下的车辆密度甚至会超过临界密度(35 veh/(km·lane)), 易造成拥堵; 而在另外6 种控制算法下则表现良好, 始终将密度控制在临界密度以下. 图7(c) 为这7 种控制算法下路段2 的车辆速度. 可以看出: 无控制情况下车辆速度有较大波动, 而在另外6 种控制算法下的车辆速度比较均匀, 且能够以较高速度通过路段2.

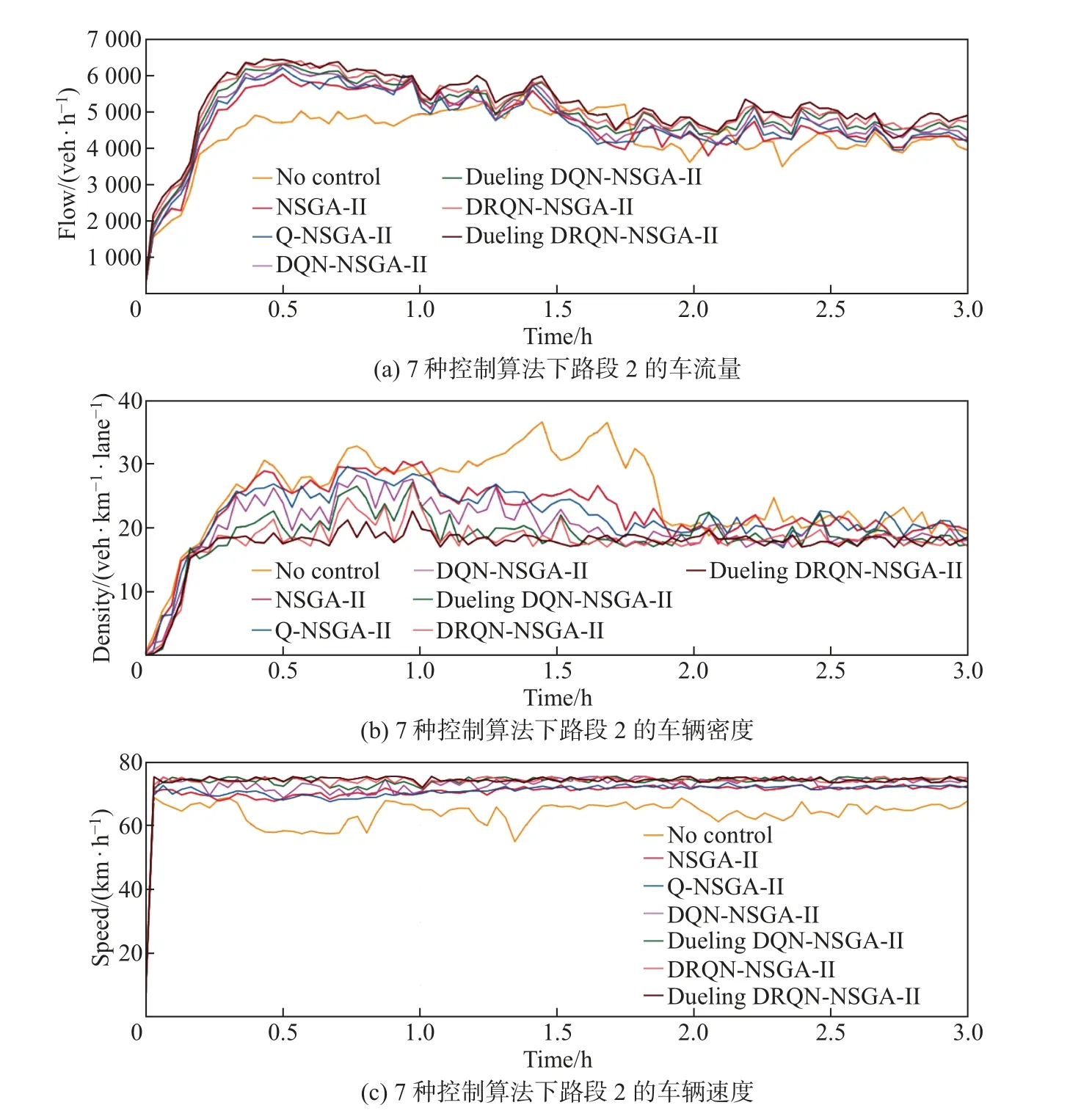
图7 7 种控制算法下路段2 的交通状态变量Fig.7 Traffic conditions of segment 2 using 7 control algorithms

图8 为无控制、NSGA-II 控制、Q-NSGA-II 控制、DQN-NSGA-II 控制、Dueling DQNNSGA-II 控制、DRQN-NSGA-II 控制和Dueling DRQN-NSGA-II 控制这7 种控制算法下的匝道排队长度. 可以看出: 无控制情况下的匝道排队长度最长, 造成拥堵, 甚至会造成近100 辆车的排队; 而其他6 种控制算法有效缓解了拥堵, 且排队长度均不超过30 辆车, 说明这6 种控制算法能够有效解决匝道控制问题.

图8 7 种控制算法下的匝道排队Fig.8 Queue length of the on-ramp with 7 control algorithms

(2) 路网性能指标评价.

本工作选取了TTS、TE 和TF 这3 种评价路网的性能指标, 其中TTS 代表路网的运行效率, TE 体现了仿真时段内路网中通行车辆对环境的影响, TF 则显示了交通控制在经济效益上的作用. 表2 为7 种控制算法下单匝道快速路网性能的评价指标.

表2 7 种控制算法下单匝道快速路网性能的评价指标Table 2 Evaluating indicators of single ramp expressway network with 7 control algorithms

由表2 可知, 在没有实施匝道控制情况下, TTS、TE 和TF 在6 种控制算法下均为最大值. 这说明在无控制情况下路网的运行效率较差, 路网中通行车辆对环境污染较多, 且燃油消耗多, 加重了经济上的负担. 在NSGA-II 算法控制下, TTS、TE 和TF 均得到了有效改善, 其中TTS 减少了9.73%, TE 减少了5.32%, TF 减少了39% 以上. 与无控制和NSGA-II 控制算法相比, 结合强化学习和NSGA-II 算法的另外5 种算法控制效果更好, 各项指标均优于无控制情况, 其中Dueling DRQN-NASGA-II 算法表现最好, TTS 减少了16.14%, TE 减少了9.56%, TF 得到了43.49% 的改善.

5 结束语

在考虑环境和能源指标的情况下, 本工作提出的Dueling DRQN-NASGA-II 算法能够有效解决城市快速路交通拥堵问题. 为了验证本算法的有效性, 首先对Dueling DRQN-NSGA-II算法进行调参, 选取最适合的超参数. 接着, 通过与NSGA-II 算法的对比, 验证了5 种算法的有效性. 之后, 分析了无控制、NSGA-II 控制、Q-NSGA-II 控制、DQN-NSGA-II 控制、Dueling DQN-NSGA-II 控制、DRQN-NSGA-II 控制和Dueling DRQN-NSGA-II 控制这7 种控制算法下路段2 的车流量、车辆密度、车辆速度和匝道排队情况.

总体而言, 相对于无控制情况, NSGA-II 算法能够缓解拥堵问题, 而结合了强化学习后的算法比NSGA-II 表现更优. 另外, Q-NSGA-II、DQN-NSGA-II、Dueling DQN-NSGAII、DRQN-NSGA-II 和Dueling DRQN-NSGA-II 控制算法也在一定程度上改善了TTS、TE和TF. 在包括NSGA-II 算法的6 种控制算法中, 效果最好的是Dueling DRQN-NSGA-II. 该控制算法使得路段2 的车流量最大、密度最小、速度最快.

此外, 本工作研究的是单入口匝道控制, 但在实际情况下, 城市快速路大多为多入口匝道.因此, 如何将深度强化学习算法应用于多匝道控制, 是未来的研究方向之一.