用角的关系,求动点的坐标

甘肃省武威第十中学(733000) 郑利年 陈国玉

二次函数为载体的与角度有关的这类问题,是近几年中考的热点之一,这类题综合性强,有利于提高同学们的解题能力. 下面将这类问题中的常见题型归纳如下,供同学们学习时参考.

1 用特殊角求动点的坐标

例1如图1,已知顶点为C(0,-3)的抛物线与x轴交于点A,B,直线y=x+m过顶点C和B.

(1)求函数y=ax2+b的解析式;

(2)抛物线上是否存在点M,使得∠MCB= 15°,若存在,求出点M的坐标;若不存在,请说明理由.

分析: (1)先将C点坐标代入y=x+m中即可求出m的值,再求出直线y=x+m与y轴的交点B的坐标,然后将B,C点坐标代入y=ax2+b中,利用方程组即可求出解析式;(2)分M在点B的上方或下方两种情况. 利用特殊角,求出直线CM与x轴的交点的坐标,从而求出直线CM的解析式,联立解析式y=ax2+b,即可求得点M的坐标.

解: (1) 将C(0,-3) 代入y=x+m, 得m= -3; 直线y=x-3 与x轴交于点B, 当y= 0 时可得x= 3,点B的坐标为(3,0),将(3,0),(0,-3)代入y=ax2+b中得∴二次函数的解析式为

(2) 存在, 如图2, ∵B(3,0),C(0,-3),∴OB=OC,∴∠OCB=45°. 分以下两种情况:

2 用两角相等,求动点的坐标

例2如图3, 直线y= -x+3 与x轴、y轴分别交于B、C两点,抛物线y=-x2+bx+c经过点B、C,与x轴的另一交点为A,顶点为D.

(1)求抛物线的解析式;

(2) 在抛物线的对称轴上是否存在一点P, 使得∠APB= ∠OCB? 若存在, 求出P点坐标; 若不存在, 请说明理由.

分析: (1) 先利用方程求出点B与点C的坐标, 代入y= -x2+bx+c中即可求得解析式;(2)分P在x轴上方或下方两种情况讨论. 由题意可知ΔBOC是等腰直角三角形,得到∠APB=45°,通过构造直角三角形,利用勾股定理建立方程即可求出点P的坐标.

解:(1)直线y=-x+3 与x轴、y轴分别交于B、C两点,则点B、C的坐标分别为(3,0),(0,3),将点B、C的坐标代入二次函数y=-x2+bx+c解析式,得解得故函数的解析式为y=-x2+2x+3;

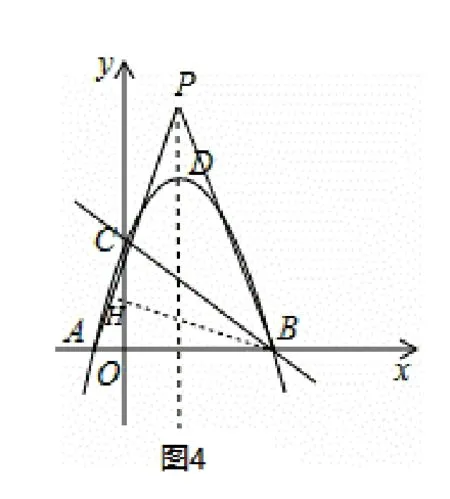
(2)存在. 因为A点与B点(3,0)关于直线x= 1 对称,所以点A(-1,0)

3 用两角和的关系,求动点的坐标

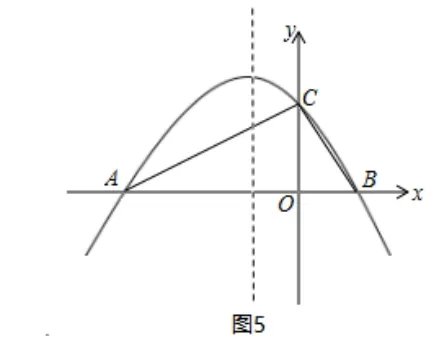
例3如图5, 已知抛物线y=ax2+bx+c与x轴交于点A,B,与y轴交于点C. 其中A(-6,0),B(2,0),C(0,3),连接AC,BC.

(1)求抛物线的解析式;

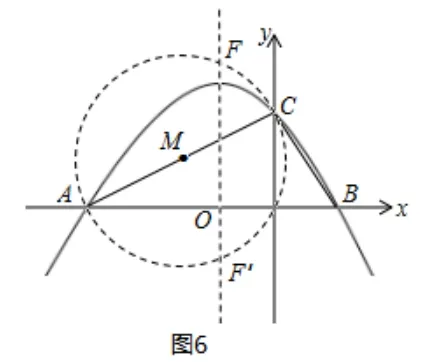
(2)抛物线的对称轴上是否存在一点F,使得∠FAC+∠FCA= 90°? 若存在,求出点F的坐标;若不存在,请说明理由[2].

分析: (1)利用交点式y=a(x-x1)(x-x2)即可求得解析式;(2)使得∠FAC+∠FCA= 90°,联想到“直径所对的圆周角为90°”和“直角三角形中,两锐角互余.”可以AC为直径作圆,与对称轴的交点即为F结合勾股即可求解.

解: (1) 抛物线与x轴交于点A,B, 设其解析式为y=a(x-x1)(x-x2), 将A(-6,0),B(2,0) 代入, 得y=(x+6)(x-2),再将C(0,3)代入,解得所以抛物线的解析式为

4 用两角倍的关系,求动点的坐标

例4已知二次函数y=ax2+bx+6 的图像开口向下,与x轴交于点A(-6,0)和点B(2,0),与y轴交于点C.

(1)求二次函数的关系式;

(2)如图7,该函数图像的顶点为D,在该函数图像上是否存在点E,使得∠EAB=2∠DAC,若存在请求出点E的坐标;若不存在请说明理由.

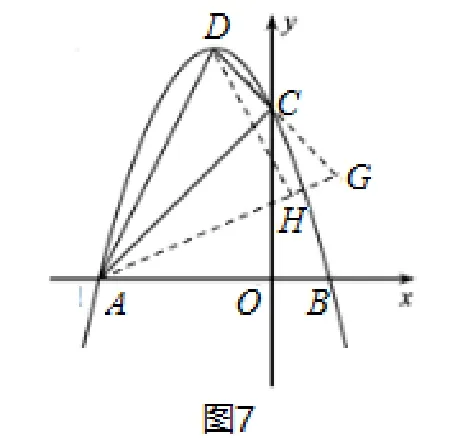
分析: (1)将点A和点B的坐标代入抛物线的解析式中,求得a,b的值,即可得到解析式;

(2) 根据勾股逆定理证得∠ACD= 90°, 延长DC至G, 使CG=DC, 连接AG, 过点D作DH⊥AG, 得到∠DAG= 2∠DAC, 利用面积法求出DH的长, 再求得sin ∠DAG= sin ∠EAB,进而得出tan ∠EAB,利用一次函数的性质得到一次函数的解析式,再与抛物线的解析式联立方程组即可求解.

总之,以二次函数为载体的角度相关问题,通常要构造直角三角形,利用勾股定理建立方程求解;或利用三角函数求出一次函数的解析式,再联立抛物线的函数式,通过解方程组求解;或通过特殊角构造直角三角形进行求解.