《鸡兔同笼》结构化教学的实践与反思

作者简介：张彦伍（1981～），男，汉族，吉林扶余人，广东省东莞市南城阳光第七小学，研究方向：小学数学教育。

摘 要：《鸡兔同笼》问题是一道经典的数学趣题，教学中培养学生解决问题能力的同时，重在理解和应用假设思想。然而“一题多解”的解题策略教学中，一节课下来师生取得的效果并不理想，学生不理解假设从何来，且用假设法解决问题的方法过于模式化。在新课标的指导下，开展结构化教学，侧重假设法学习和理解，借助思维导图呈现可视的结构，“深度”掌握数学模型，促进学生思维发展。

关键词：结构化教学；鸡兔同笼；假设思想

中图分类号：G623.5

文献标识码：A

文章编号：1673-8918（2023）32-0100-04

《义务教育数学课程标准（2022年版）》在设计体现结构化特征的数学课程内容中指出：“重点是对内容进行结构化整合，重视数学结果的形成过程；根据学生的年龄特征和认知规律，适当采取螺旋式的方式，逐渐拓展和加深课程内容，适应学生的发展需求。”结构化教学体现了学科内容整体性和一致性，学生从学习的内容关联中体会到核心概念，并在其后学习中进行反复运用和强化，进而促进核心素养的发展。《鸡兔同笼》是一道经典的数学趣题，引导学生在感受数学文化魅力的同时，培养学生解决问题的能力，重在假设思想。对此，如何帮助学生梳理与《鸡兔同笼》相关的知识，更好地理解和掌握假设思想，呈现完整的结构化学习过程，促进学生的思维发展呢？文章笔者将以《鸡兔同笼》一课为例，尝试开展结构化教学实践。

一、课前思考，分析学情

笔者回顾教学中发现师生在本节课学习中遇到的困难如下：从学生角度来看：一是假设从何而来？在教学中往往“假设”一词都是教师提出，引导学生进行解题，学生不理解为什么要进行“假设”；二是模型的掌握固化，即学生对《鸡兔同笼》系列数学模型更多的是一种“公式”的掌握，无法变通解决“鸡、兔”以外的相关问题。教学中我们引导学生掌握一定的数学模式是有必要的，但不能是模式化。从教师角度来看：人教版教材提倡“一题多解”，让学生体验解决问题的多样化，了解列表法、假设法和画图法等，然而一节课下来多种方法的呈现，学生掌握并不理想。调查发现，在实际解决《鸡兔同笼》问题中，学生在多种解题方法中用到假设法的约占80%以上。因此，笔者将用学生已有学习经验和需求进行教学，设计符合学生的学习情境感知“假设”的由来，在新旧知识对比中掌握数学模型，面对多种解法中采取“任弱水三千，我只取一瓢”，即側重假设法教学。

二、寻找关联，梳理结构

经笔者对教材的知识梳理，与本节课相关联的知识点包括以下：第一，三年级上册《多位数乘一位数》和三年级下册《除数是一位数的除法》的学习中学生已经掌握了乘除法计算能力，能够结合“单一”的数学信息解决相应的数学问题，为《鸡兔同笼》问题中乘除法计算解决问题作了铺垫；第二，三年级上册《测量》中《吨的认识》这节课学生学习了列表法解决问题，而且题目中大小车和课后的练习题大小船与《鸡兔同笼》中的鸡兔问题基本相同。因此，这些已有的学习经验不仅为本节课解决问题的方法提供了帮助，也为《鸡兔同笼》问题的数学模型形成提供了依据。

据此，《鸡兔同笼》的教学定位：一是从“单一”信息（笼子里全是鸡或全是兔）导入新知，为假设的由来作好铺垫；二是在观察与对比“单一”信息与《鸡兔同笼》问题中，初步形成《鸡兔同笼》数学模型；三是回顾与《鸡兔同笼》的相关知识，即《吨的认识》例题，引出列表法解决问题，并借此优化方法。同时用大小车、大小船等知识的回顾及引导学生尝试列举，逐步加深数学模型认知和运用，由浅入深，从而更好地发展学生的核心素养。

三、实践课堂，呈现结构

（一）引问新知，回顾旧知

师：同学们，你知道《鸡兔同笼》问题吗？能介绍下吗？（生答）

师：你们知道的可真多，为你们点赞。可是当初我没有学的时候，想得很简单，同学可别笑话我，知道我是怎么想的吗？

课件出示（一个笼子里全是鸡，或者全是兔）

师：我当时就认为很多只鸡在同一个笼子，很多只兔在同一个笼子。这样的问题多简单，你们看如果笼子里有35只鸡，能算出有多少只脚吗？

生1：能，一共70只，用35×2就可以了。

师：为什么要乘2呢？

生：因为一只鸡有2只脚。

师：是的。如果笼子的鸡脚一共有60只，能知道有多少只鸡吗？

生：30只。

师：笼子里有35只兔子，知道有多少只脚吗？

生2：一只兔子4只脚，一共有35×4=140只脚。

师：真棒。如果笼子里共有80只脚，有多少只兔子呢？

生3：80÷4=20只兔子。

师：同学们，你们看，这样的鸡、兔同笼问题多简单。

（二）新旧关联，理解假设

1. 数学文化

师：《鸡兔同笼》问题是1 500年前我国古代名著《孙子算经》中记载的一道数学趣题。（出示课件）

师：在生活中产生的数学问题，可以看出当时我们的先辈对数学的热爱和他们的智慧，能读懂题的意思吗？

2. 巧引假设

师：见到真正的《鸡兔同笼》问题，再和我想象的对比下，有什么感觉？

生：变难了。

师：是啊！有鸡也有兔，混合在一起多难算啊！所以我就在想：笼子里装的……就好了。同学们，你知道我在想什么吗？

生1：你肯定在想如果笼子里全是鸡就好了。

师：哇！你真懂我的心思。

生2：还有，笼子里全是兔子也行。

师：谢谢，我们已经是知己了。我当时的确就是这样想的。

师：那笼子里能全是鸡或者全是兔子吗？

生：不能，题中都说了鸡和兔同笼的。

师：是啊，这只不过是我的个人想法，不是真的。在数学中像老师这样的想法，称为假设。

师：这样的假设能解决鸡兔同笼问题吗？

生：不知道。

师：那我们不妨试一试，敢于想象，敢于尝试，或许会有新的收获。

3. 运用假设

师：假设笼子里全是鸡会有什么结果呢？

生：腿数不够。

师：为什么不够？

生1：因为差兔子啊，把兔子当成了鸡，一只兔子就少算了2只脚。

师：确实，兔子肯定也为难了。那一共少多少只脚呢？你们知道吗？

生：一共少24只。

师：怎样计算的？

生2：因为一只鸡2只脚，35只鸡一共有35×2=70只脚，题中说一共有94只脚，还差24只。

师：为了便于我们更好地理解，也可以借助画图的方法演示，一起看下。（课件演示）

师：老师用算式把这个过程记录下来。那24只脚是谁的呢？

生3：是兔子的呀，因为刚才不是说了把兔子看成鸡。

师：明白了，那现在把脚还给兔子吧，应该怎么去还呢？

生4：给一只鸡加上2只脚，就变成兔子了。

师：为什么加2只脚？

生5：因为一只兔子比一只鸡多了2只脚。

生6：他的意思是说，假设笼子里全是鸡，那兔子也变成了鸡，一只兔子就少算了2只脚，所以24要除以2，是12只兔子的脚数。

师：谢谢你这么详细的解释。原来这个“2”是一只兔子和一只鸡相差的脚数，利用这样的数量关系，我们算出了笼子里兔子的只数共有12只，那鸡就是多少只？

生7：用35-12就是鸡的只数了，鸡有23只。

师：笼子里有23只鸡，12只兔，这个只数到底对不对呢？大家能验算下吗？

生8：12×4+23×2=94，说明是正确的。

师：真好！看来运用假设这个方法还能解决问题呢。

4. 自主探究

师：同学们，再来一起看下假设全是鸡的计算过程，我们先计算了35只鸡的总脚数，再用笼子里鸡兔的总脚数94-70得出了少的脚数，因为把兔子看成了鸡，一只兔子就少算了2只脚，所以用24÷2就得出了兔子的只数，最后也就得到了鸡的只数。

师：如果假设全是兔，你能像这样列式解决吗？请大家试一试。（学生完成后汇报）

生1：假设笼子里全是兔，笼子里共有35×4=140只，140-94=46表示比笼子里规定多出的脚数，这次假设全是兔，就是把鸡也当成了兔，一只鸡就多出2只脚，所以用46÷2=23只就算出了鸡的只数，用35-23=12只就是兔子的只数了。

师：为他完整地解答鼓掌！那结果对不对呢？

生2：不用计算了，和上面假设全是鸡的答案一样，所以计算是正确的。

师：真棒！通过刚才大家的计算，再次验证了假设法的确不错。

（三）对比分析，形成模型

1. 初识模型

师：同学们，我们一起来对比下，老师想象的“鸡、兔同笼”问题和真正的《鸡兔同笼》问题，它们之间有什么不同的地方？

生1：老师想的笼子里全是鸡或者全是兔，而《鸡兔同笼》里既有鸡也有兔。

生2：想的题比较简单，而《鸡兔同笼》问题比较难。

师：从哪里看出了簡单和难呢？

生3：全是鸡或全是兔，就给一个数学信息，《鸡兔同笼》既有鸡，也有兔的比较复杂。

师：是的，我想象的问题中给出的数学信息是单一的，而《鸡兔同笼》问题就像是把这两个单一不同的条件合在了一起。其实像这样的问题，我们也并不陌生，三年级的时候就遇到过。

2.优化列表

师：（出示课件，如图1）同学们，能看出这题中的“鸡”和“兔”吗？

生：大车是兔子，小车是鸡。

师：还记得怎样解决这道题的吗？（课件出示列表法）当时我们是用列表法解决。

师：我们也用列表法来解决下今天学习的《鸡兔同笼》问题吧。（出示表格）如果鸡有1只，兔子就要有34只，一共有多少只脚呢？

生：1×2+34×4=138

师：是的，如果鸡有2只，兔子就要有33只，一共有136只脚。如果鸡有3只，……以此类推，要算到哪里呢？

生：鸡有23只，兔子有12只。

师：对的。运用列表法解决你有什么感觉？

生：太麻烦了。

师：不过，这里面也有简便的地方，你发现了吗？

生1：我发现了，多一只鸡，少一只兔子，总脚数就少2只。

师：真是善于观察的孩子！如果反过来看，又有什么发现？

生2：多一只兔子，少一只鸡，总脚数就多2只了。

师：了不起！所以我们也可以运用这样的规律去解决鸡兔同笼问题。但和假设法对比，可能假设法略胜一筹。大家选择自己喜欢的方法就可以。

3. 深化模型

师：课后还有一题，大家请看。（出示课件，如图2）

师：能看出这题中的谁是“鸡”，谁是“兔”吗？

生：大船是鸡，小船是兔。

师：是的，它们都和鸡兔同笼问题一样，里面都是由两个不同的数学信息组成。笼子装的是鸡和兔，就可以叫作《鸡兔同笼》问题，那同学们再想下，刚刚这两道题其实也可以有自己的名字，叫什么问题呢？

生1：卡车问题。

生2：大小船问题。

师：鸡兔同笼是一个代表性的问题，只要像它们这样，将两个不同的数学信息融合在一起，就可以设计出一道问题来。同学们，大胆地思考下，生活中还有什么样的相似问题呢？你能举例说一个吗？

生3：5元钱和1元钱放在一起，可以组成金钱问题。

生4：八爪鱼和兔子放在一起，鱼兔问题。

生5：牛和鸡在一起，牛鸡问题。

……

师：真是爱思考的孩子，为你们点赞。像这样的问题在我们生活中有很多，只要将两个不同的“单一”数学信息放在一起，就可以组成是“鸡兔同笼”问题了。

四、反思教学，解析结构

通过结构化教学的开展，加深了学生对《鸡兔同笼》问题的数学模型的理解，并能更好地运用假设法解决相关的问题。

（一）以旧知引新知，搭建认知结构

人的认知规律特点是“温故知新”，尤其对学生更加適合。本节课的教学从学生角度出发，设计适合学生的学习情境，以教师初学时猜想的“单一”数学信息（即一个笼子里全是鸡或全是兔）的导入回顾旧知，唤起学生已有的学习经验。在这个学习过程中，沟通了新旧知识的关系，为假设思想解决问题作好了铺垫，激发了学生尝试探究新知、获取新知的需求，提高学生“主动学习”的积极性。以旧知引出新知学习的方式，体现了“降维思想”，从学生已有的学习经验和生活经历中开展教学，搭建符合学生认知的桥梁，符合结构化教学要求。

（二）用关联比不同，探究模型结构

《鸡兔同笼》是一道典型的逻辑推理问题，部分学生学习后只识“鸡兔”，不识“模型”。为了更好地让学生在学习中认清“模型”，教学中联系学生已有的学习“单一”数学信息问题与鸡兔同笼问题进行对比不同，发现鸡兔同笼问题好比将两个不同的“单一”数学信息捏合而成，在对比中学生初步感知模型结构。再回顾三年级上册《吨的认识》中例题大小卡车和课后练习题大小船，寻找“鸡”和“兔”，深化模型的探究，引导学生感知《鸡兔同笼》只是一个典型的代表，还可以有“大小卡车问题”“大小船问题”，以此让学生列举相关的问题。在这个学习过程中，学生探究《鸡兔同笼》问题的模型结构是由浅入深、螺旋上升的方式，体现了深度学习，为学生解决《鸡兔同笼》的相关问题打下了良好的基础。

（三）理知识画导图，呈现可视结构

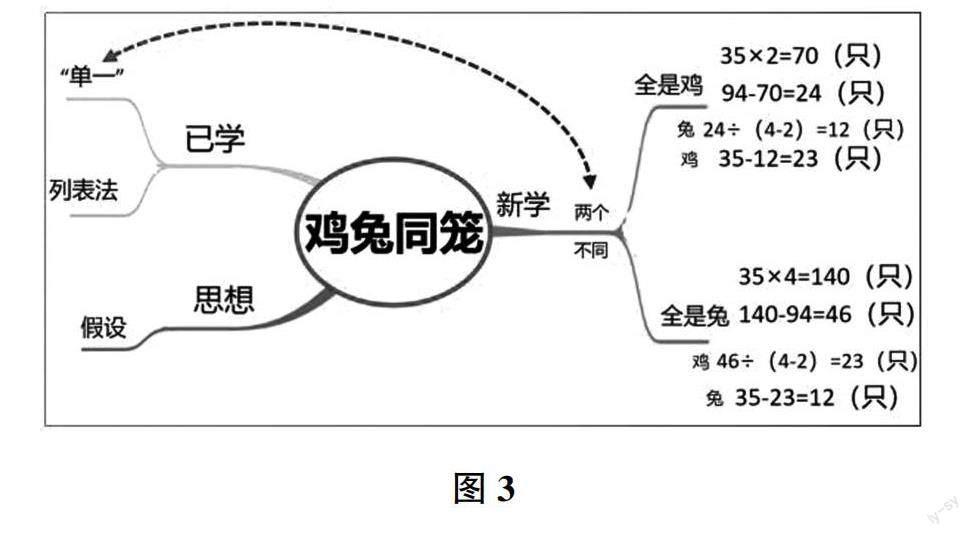
开展结构化教学实现了整体意义关联，思维结构发展，致力于将碎片化知识连点成线，将割裂化的方法关联成体，将浅表化的思维引向深刻。然而在平常的教学中，这样的知识结构多数是隐形的，不可见的，教师努力构建和表达，学生却无法感知和获取。因此，在教学中为了更好地让学生掌握好知识结构，笔者借助思维导图作为板书设计（如图3），将隐形的知识结构直观地呈现出来，借助板书看到知识结构的“前”与“后”，这种方式利于学生对整体的知识结构深度理解和应用。（文章由广东省王金发名师工作室指导）

参考文献：

［1］中华人民共和国教育部.义务教育数学课程标准［M］.北京：北京师范大学出版社，2022：2-3.

［2］吴玉国.指向学习经验生长的结构化学习策略［J］.江苏教育研究，2022（29）：26-30.