钢管煤矸石混凝土的徐变模型及长期变形计算方法

王庆贺,张 岩,张玉琢,张信龙,岳 崇

(1.沈阳建筑大学土木工程学院,辽宁 沈阳 110168;2.哈尔滨工业大学结构工程灾变与控制教育部重点实验室,黑龙江 哈尔滨 150090;3.中国建筑第二工程局有限公司,北京 100000)

煤矸石作为混凝土骨料以解决固废利用由来已久。研究发现,与普通混凝土相比,煤矸石混凝土力学性能有一定程度的欠缺,且变异性较大,使其在结构工程推广应用中受到了一定的限制[1-4]。为更好地解决困扰自燃煤矸石应用的难题,在自燃煤矸石混凝土外部增设钢管,制成钢管煤矸石混凝土,充分利用钢管的约束作用改善煤矸石混凝土的力学性能,为煤矸石资源化利用提供了有效途径[5-8]。徐变引起的结构变形和内力重分布等问题,直接影响到结构的长期使用性能[9-11]。全取代的煤矸石骨料混凝土的弹性模量降低了30%,使得煤矸石混凝土徐变增长显著[12]。李永靖[13]、刘德慧等[14]通过数据拟合得出考虑煅烧温度、取代率、水灰比的煤矸石混凝土徐变模型,并说明了各因素对煤矸石混凝土徐变的影响程度从大到小依次为煅烧温度、煤矸石取代率、水灰比。Z.P.Bazant[15]分析了混凝土徐变的影响因素,提出了水泥净浆和骨料体积分数对混凝土徐变系数的影响规律。其他学者通过引入不同影响系数在各自领域对公式进行修正,证实了公式对于徐变性能预测的可靠性[16-17]。目前,针对自燃煤矸石混凝土,尚无适用的徐变模型可供参考。此外,钢管煤矸石混凝土中核心混凝土徐变量的增加导致构件长期力学性能发生变化,应当对于钢管煤矸石混凝土的徐变性能进行深入研究。

综上所述,笔者基于Bazant徐变模型,考虑煤矸石取代率和骨料体积分数的影响,提出煤矸石混凝土徐变增大系数,并引入普通混凝土徐变模型,得到煤矸石混凝土徐变模型,通过参数分析确定影响煤矸石混凝土徐变性能的关键影响因素;采用基于龄期调整的有效模量法对钢管煤矸石混凝土徐变变形进行预测,并与逐步积分法所得预测结果进行比较,提出钢管煤矸石混凝土柱长期变形的计算方法,提高预测模型的可靠性和安全性,为煤矸石混凝土的工程应用提供更可靠的理论依据。

1 煤矸石混凝土徐变预测模型

1.1 煤矸石混凝土徐变模型

考虑到煤矸石混凝土与普通混凝土差异在于粗骨料,将骨料体积分数具体到粗骨料体积分数,得到了水泥砂浆徐变系数、粗骨料体积分数对普通混凝土徐变系数影响的关系式,如式(1)～式(2)所示:

(1)

(2)

将普通混凝土徐变影响关系类比到煤矸石混凝土,得到了煤矸石混凝土的徐变系数影响关系式,如式(3)～(4)所示:

(3)

(4)

联合式(1)～式(4),可以得到煤矸石徐变增大系数κ:

(5)

通过与普通混凝土弹性模量关系得到煤矸石混凝土弹性模量[12]:

ESCGAC=(1-0.3r)ENAC.

(6)

式中:r为煤矸石粗骨料取代率。

考虑弹性模量与体积的Voigt模型[18]:

ENAC=VCAENCA+ENM(1-VCA).

(7)

煤矸石粗骨料弹性模量则需要确定取代率对弹性模量的影响,用式(7)对等效煤矸石粗骨料弹性模量进行预测,并基于测定的骨料弹性模量关系ESCGA=1/3ENCA[12,19],得到等效煤矸石骨料弹性模量:

(8)

式中:r为煤矸石粗骨料取代率;ΕNM为砂浆弹性模量。

根据文献[20]可以得到混凝土弹性模量与混凝土骨料弹性模量关系。

ENAC/ENCA=0.5.

(9)

依据文献[21]的研究成果,煤矸石骨料与普通骨料泊松比相近,即μSCGAC=μNAC=0.2,由式(2)、式(4)和式(5)可得到煤矸石取代率和粗骨料体积分数综合影响下的徐变增大系数:

(10)

1.2 各模型预测结果及参数分析

目前国际上常用的徐变模型主要有欧洲规范EC2、美国规范ACI 209、GL2000以及B 3模型[22]。将煤矸石混凝土徐变增大系数引入到徐变模型中,得到4种煤矸石混凝土徐变模型。参考文献[13]的配合比对煤矸石混凝土徐变性能进行对比,其中水灰比为0.45,水泥用量350 kg/m3,砂率采用0.35,抗压强度为30 MPa,煤矸石粗骨料取代率分别取0、50%、100%。构件理论厚度为50 mm,首次加载龄期为28 d,相对湿度为60%环境下持续加载50 a,得到徐变预测结果(见图1)。可以发现,随着煤矸石骨料取代率增加,各模型预测的徐变系数均呈增加趋势,且增加速率逐渐加快,50%取代率煤矸石混凝土相比普通混凝土(取代率为0)徐变系数增幅在10%以内;100%取代率煤矸石混凝土相比普通混凝土徐变系数增幅约为30%。此外,初期徐变系数增长迅速,之后增长逐渐减缓,以100%取代率煤矸石混凝土为例,在EC 2、ACI 209、GL 2000、B 3模型预测结果中,持续加载5a煤矸石凝土徐变系数约为持续加载1a煤矸石凝土徐变系数的1.26、1.28、1.49、1.82倍。

图1 徐变系数随时间变化规律Fig.1 Development laws of creep coefficient with time

为分析混凝土配置中常用参数对煤矸石混凝土徐变性能的影响,选取参数范围如下,砂率为30%～40%,相对湿度为30%～80%,抗压强度为30～60 MPa,构件厚度为20～1 500 mm。图2为各参数对煤矸石混凝土徐变系数的影响。可以发现,徐变系数与相对湿度、抗压强度、砂率、构件尺寸呈负相关,其中相对湿度和抗压强度为主要影响因素。以取代率为100%煤矸石混凝土为例,砂率由30%增至40%时,采用EC 2、ACI 209、GL 2000、B 3模型预测的徐变系数分别降低了7.6%、5.3%、7.6%和8.0%。相对湿度由30%增至80%时,徐变系数分别降低了43%、31%、38%和36%。抗压强度由30 MPa增至60 MPa时,采用EC 2、B 3模型预测的徐变系数分别降低了46%和20%。当构件厚度小于500 mm时,徐变系数下降幅度较快;构件厚度为500 mm时,采用EC 2、ACI 209、GL 2000、B 3模型预测的徐变系数下降幅度可达到大尺寸构件(构件厚度为1 500 mm)下降幅度的87%、99%、55%和97%;当构件厚度超过500 mm以后,构件厚度对徐变系数影响大幅减少,徐变系数基本保持平稳趋势。

图2 各参数对煤矸石混凝土徐变系数的影响Fig.2 Influence of parameters on creep coefficient of CGAC

2 钢管煤矸石混凝土长期变形

2.1 长期性能分析方法

钢管煤矸石混凝土构件在长期荷载作用下,核心混凝土所承担的荷载会随时间增长不断降低,发生应力重分布现象。考虑混凝土时效作用[23],在变荷载作用下的核心混凝土长期变形可通过下式计算:

εc(tk)-εsh(tk)=σc(t0)J(tk,t0)+

(11)

式中:εc(tk)为tk时刻核心混凝土的总变形量;εsh(tk)为tk时刻混凝土收缩应变;σc(t0)为t0时刻核心混凝土的应力;J(tk,t0)为从t0开始加载到tk时刻的混凝土徐变函数。

直接计算式(11)中的积分部分比较困难,可采取逐步积分法(SSM)或基于龄期调整的有效模量法(AAEM)进行计算。

2.1.1 逐步积分法

逐步积分法在进行徐变计算时,将时间t离散为t0,t1,t2,…,tk,共k个时间段[24],利用缩短时间间隔的方法来控制误差,因此所得到的计算结果较为精准,得到的徐变计算公式如式(12)～(15)所示:

εc(tk)-εsh(tk)≅σc(t0)J(tk,t0)+

(12)

Ec1kεsh(tk).

(13)

(14)

Ec2kj=

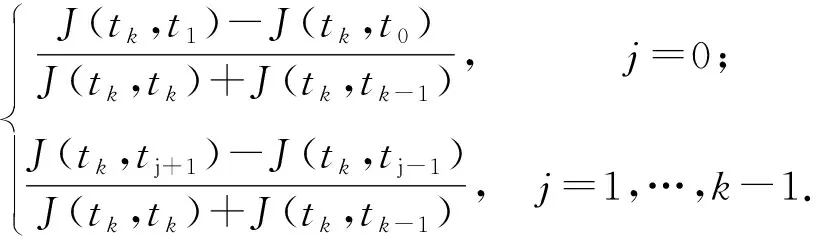
(15)

式中:εc(tk)为tk时刻核心混凝土的总变形量;εsh(tk)为tk时刻混凝土收缩应变;σc(tk)为tk时刻核心混凝土的应力;J(tk,tk-1)为从tk-1开始加载到tk时刻的混凝土徐变函数。

2.1.2 基于龄期调整的有效模量法

发生线性徐变时,混凝土徐变大小取决于应力与弹性模量变化,基于龄期调整的有效模量法[25-26]考虑了混凝土初始加载应力及持荷过程中的应力变化,并在混凝土弹性模量上增加了老化系数,以考虑混凝土老化对徐变终值的影响,得到的徐变计算公式如式(16)～(17)所示:

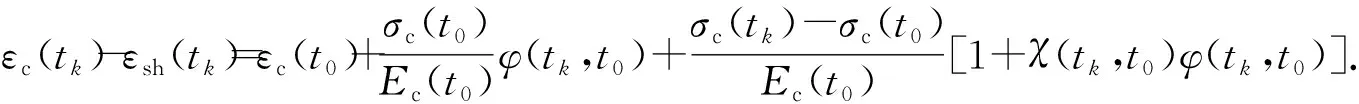
(16)

χ(tk,t0)=[1-exp(-(0.09+

0.686φ(tk,t0))]-1-[φ(tk,t0)]-1.

(17)

式中:φ(tk,t0)为从t0开始加载到tk时刻的混凝土徐变系数;χ(tk,t0)为从t0开始加载到tk时刻的混凝土老化系数。

采用逐步积分法进行构件长期变形分析时,虽然计算精度较高,但如式(12)所示,计算第k步变形时,需调用前k-1步核心混凝土应力、应变进行迭代计算,计算相对繁琐,不便在实际工程中使用。与逐步积分法不同,基于龄期调整的有效模量法对迭代计算进行了代数近似求解,是目前常用的计算钢管混凝土徐变变形的方法,由于煤矸石混凝土徐变高于普通混凝土,需要对比各徐变模型下基于龄期调整的有效模量法与逐步积分法的差异。

2.2 徐变预测模型对比分析

按照参考文献[13]参数配合比配置钢管煤矸石混凝土,并增加轴压比为0.4、含钢率为10%两个条件。使用逐步积分法和基于龄期调整的有效模量法预测钢管混凝土长期力学性能,得出钢管煤矸石混凝土徐变应变结果(见图3～图6)。随着煤矸石骨料取代率增加,各模型预测的钢管混凝土徐变应变均呈增加趋势,且增加速率逐渐加快。EC 2、ACI 209、GL 2000、B 3模型中50%取代率钢管煤矸石混凝土相比钢管普通混凝土(取代率为0)徐变应变增幅约为17%;100%取代率钢管煤矸石混凝土相比普通混凝土徐变应变增幅约为50%。相对于煤矸石混凝土徐变系数,钢管煤矸石混凝土徐变应变中融入了骨料弹性模量的影响,放大了不同取代率钢管煤矸石混凝土之间徐变应变的差异。

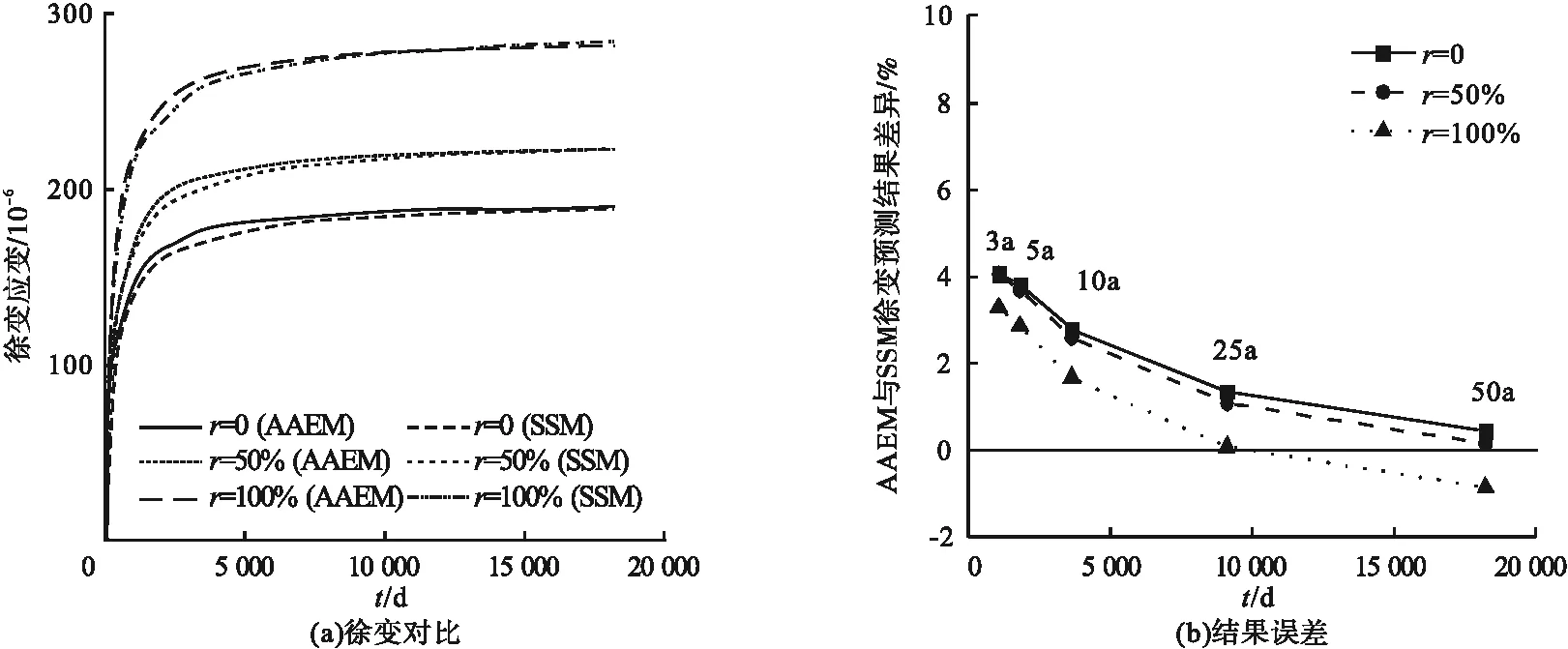
图3 EC 2模型的有效模量法与逐步积分法预测结果对比Fig.3 Comparison of AAEM and SSM prediction results of EC 2 model

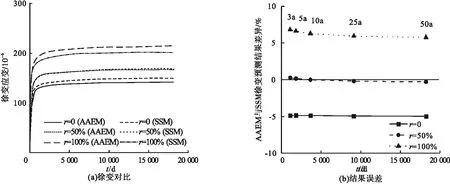
图4 ACI 209模型的有效模量法与逐步积分法预测结果对比Fig.4 Comparison of AAEM and SSM prediction results of ACI 209 model

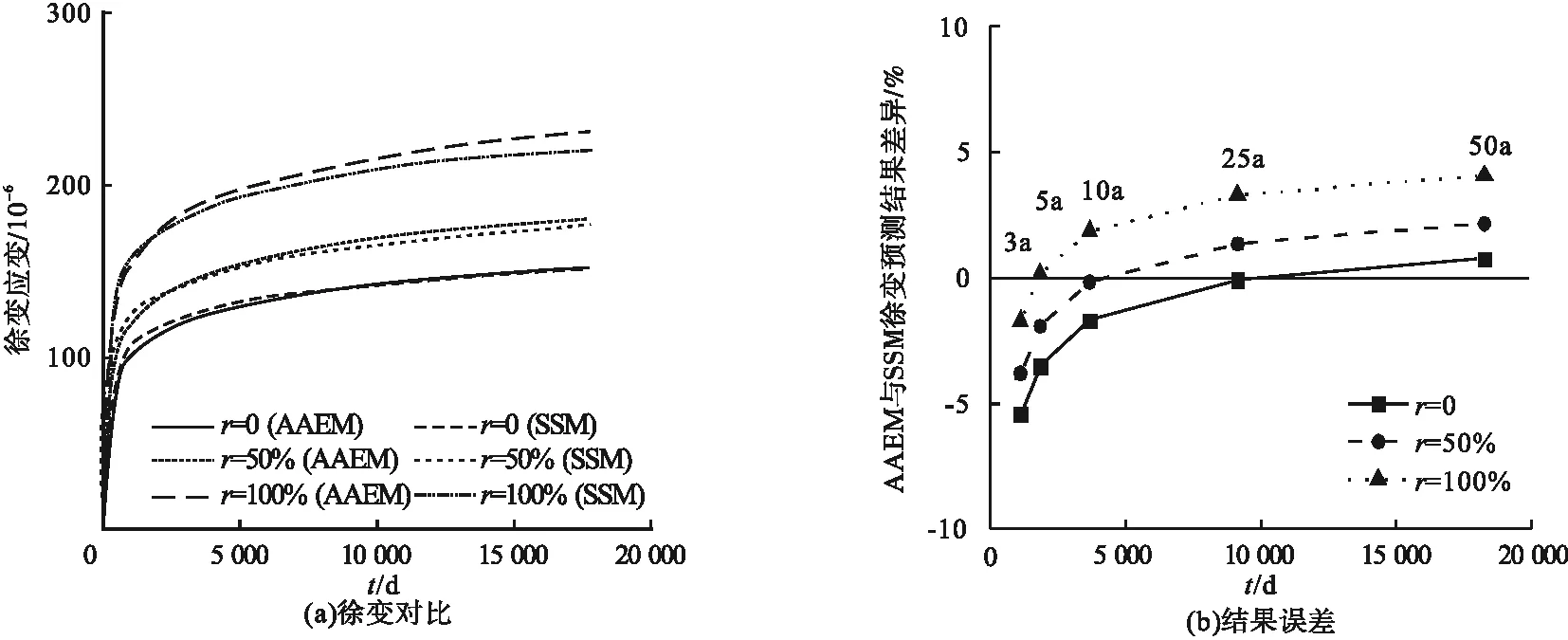
图5 GL 2000模型的有效模量法与逐步积分法预测结果对比Fig.5 Comparison of AAEM and SSM prediction results of GL 2000 model

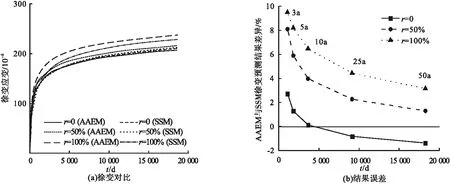
图6 B 3模型的有效模量法与逐步积分法预测结果对比Fig.6 Comparison of AAEM and SSM prediction results of B 3 model

由图3～图6可知,随着时间的增长,基于龄期调整的有效模量法预测精度逐渐提高,但取代率的增加会放大两种方法预测结果的偏差。基于龄期调整的有效模量法在预测钢管煤矸石混凝土徐变应变时与逐步积分法之间的差异均在10%以内,相比钢管普通混凝土构件6%左右的最大偏差有所增加[23]。对于持荷50 a钢管煤矸石混凝土徐变应变的预测结果,四种模型误差均在6%以内,EC2模型差异最小,约为1%;ACI209模型差异最大,为5.74%。基于龄期调整的有效模量法与逐步积分法预测结果较为吻合,可使用基于龄期调整的有效模量法替代逐步积分法应用于钢管煤矸石混凝土徐变应变计算。

3 结 论

(1)煤矸石混凝土徐变性能与普通混凝土徐变性能的差异可以通过煤矸石取代率和粗骨料体积分数进行计算。

(2)煤矸石混凝土的徐变系数与取代率呈正相关,与相对湿度、抗压强度、砂率、构件尺寸呈负相关。相对湿度和抗压强度为主要影响因素,50%取代率的煤矸石混凝土较普通混凝土徐变系数增幅约为10%,100%取代率的煤矸石混凝土增幅约为30%;相对湿度由30%增至80%时,徐变系数约降低40%;抗压强度由30 MPa增至60 MPa时,徐变系数约降低40%;构件厚度达到500 mm以后,对徐变系数影响不显著;外部钢管可有效降低煤矸石混凝土的徐变变形。

(3)基于龄期调整的有效模量法与逐步积分法预测结果差异在10%以内,由于前者更方便快捷,因此,在工程中可采用基于龄期调整的有效模量法对钢管煤矸石混凝土徐变性能进行预测。