基于XFEM钢桥面板-U肋焊缝疲劳裂纹扩展规律及其影响因素分析

王占飞,韩迎秋,何志成,王 维

(1.沈阳建筑大学交通与测绘工程学院,辽宁 沈阳 110168;2.珠海交通工程技术有限公司,广东 珠海 519060;3.中建铁路投资建设集团有限公司,北京 102627)

近年来,正交异性钢桥面板因其具有轻质高强且便于施工等优点被广泛使用[1]。但由于正交异性钢桥面板本身构造特点易引起面板、纵肋、横肋的面外变形,从而在循环载荷下产生疲劳开裂的问题[2]。据统计,在服役期间大约 90%的正交异性钢桥面板结构失效是由疲劳开裂引起的[3]。因此,对现役钢桥疲劳细节的裂纹扩展路径和裂纹疲劳寿命预测是一个至关重要的问题。

扩展有限单元法(Extended Finite Element Method,XFEM)作为一种新兴模拟裂纹扩展的数值方法,不仅保留了传统有限单元法的优点,并且克服了传统有限单元法在裂纹扩展过程中需要对裂纹尖端的网格进行重划分的缺点[4]。因此该方法受到众多学者关注。殷晓磊等[5]应用XFEM研究了高强钢丝的裂纹扩展规律。H.Zarrinzadeh等[6]应用XFEM分析了复合材料中不同裂纹取向的管道断裂行为。刘占生[7]基于XFEM模拟了舰船蒸汽轮机叶片裂纹萌生和扩展情况。林铁军等[8]应用XFEM模拟研究了钻杆裂纹扩展的过程。上述国内外学者的研究表明,XFEM在模拟裂纹扩展的问题中具有一定的可行性和准确性。基于此,笔者基于XFEM研究正交异性钢桥面板-U肋焊缝处疲劳裂纹扩展规律,利用ABAQUS有限元软件建立了3U肋正交异性钢桥面板数值分析模型,将复杂的三维问题简化为平面问题,并通过改变初始裂纹长度、面板厚度和应力比(应力幅值曲线中最小应力与最大应力的比值)等变量研究不同条件下钢桥面板-U肋焊缝的疲劳裂纹扩展规律,系统探究了各因素对其疲劳性能的影响,为探明钢桥面板疲劳裂缝问题提供参考依据。

1 XFEM分析及模型验证

1.1 扩展有限元

在疲劳分析中,裂纹模拟是一个复杂的问题。传统的有限单元法是基于牵引分离准则模拟裂纹扩展,而其应用的前提是保证材料的连续性。因此,基于传统有限单元法模拟的裂纹,其只能沿网格边界传播,而不能直接穿过单元,故降低了裂纹的模拟精度。除此之外,为保证材料在裂纹尖端的连续性,有限单元法还需在每次迭代计算前重新划分其裂纹尖端的富集区域网格,这也极大提高了计算成本。

T.Belytschko[9]于1999年首次提出了扩展有限单元法。该方法包含了传统有限元法优点的同时,兼具了跳跃函数和裂纹增强函数来提高裂纹的模拟精度。此外,为使裂纹能够在单元上扩展,引入了具有虚拟节点的内聚分段法来解决裂纹扩展引起的不连续性问题,从而提高裂纹扩展的精度。如图1 所示,在分析前对每个原始节点施加了虚拟节点,单元尚未开裂前,虚拟节点被严格约束在原始节点上。随着裂纹的扩展,裂纹将单元一分为二,此时单元的连续性也被破坏。而由于预先设置虚拟节点,故这两个不连续的区域将分别包含一组原始节点和虚拟节点。因此,由裂纹扩展引起的不连续问题也将转化为两个连续问题来解决。

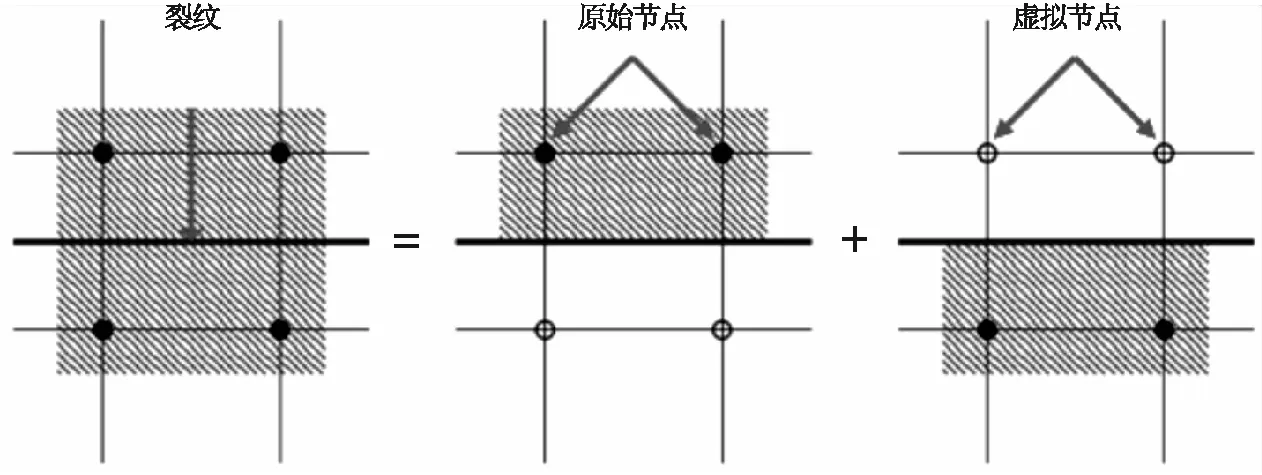
图1 扩展有限单元法基本原理Fig.1 Basic principles of extended finite element method

1.2 基于XFEM的有限元模型及验证

为验证基于XFEM的有限元分析方法能够准确预测面板与U肋焊缝的裂纹扩展路径及疲劳寿命,笔者参照文献[10] 中的正交异性钢桥面板与U肋焊缝疲劳加载试验,利用ABAQUS软件建立了与试验试件相同尺寸的有限元分析模型。试验试件采用Q345qD钢制作,顶板厚度16 mm、U肋厚度8 mm,面板与U肋为单面焊接,熔透率为80%。具体尺寸及加载方式见图2,Q345qD钢材料参数见表1,基于XFEM的有限元模型如图3所示。网格设置:主要区域网格长×宽为3 mm×3 mm,而裂纹扩展区域网格长×宽加密为0.1 mm×0.1 mm。疲劳载荷工况:应力比R=-1的拉-压正弦波作为加载频率,并分别考虑了100 MPa、80 MPa、55 MPa三种应力幅值进行加载。

表1 Q345qD材料参数Table 1 Material parameters of Q345qD

图2 正交异性钢桥面板与U肋焊缝疲劳试验试件尺寸Fig.2 Fatigue test specimen size of welds between orthotropic steel bridge deck and U-rib

图3 扩展有限元模型Fig.3 Extended finite element model

面板-U肋焊缝在三种应力幅值下的疲劳裂纹扩展路径如图4所示。图4(a)为试件试验时的裂纹扩展情况,在三种应力幅值下的裂纹扩展路径一致。图4(b)、图4(c)、图4(d)分别为应力幅值为100 MPa、80 MPa、55 MPa有限元分析得到的疲劳裂纹扩展情况。由图4可知,模型中裂纹最先萌生于焊跟处,并沿板厚基本呈垂直方向扩展,应力幅值大的,裂纹扩展较快。

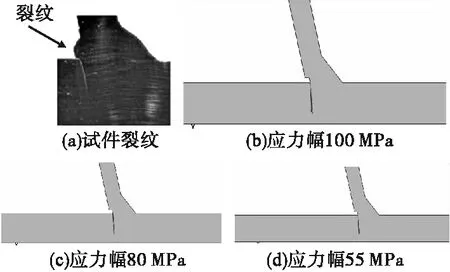
图4 试验试件与XFEM疲劳裂纹扩展路径Fig.4 Comparison of fatigue crack propagation path between test specimen and XFEM

有限元分析所得三种应力幅值下面板-U肋焊缝的疲劳寿命与试验结果对比如图5所示。裂纹萌生寿命和断裂寿命分别依据参考文献[10]:以疲劳细节处裂纹开始扩展时的加载次数作为裂纹萌生寿命,以裂纹扩展至面板厚度70%时的加载次数作为断裂寿命。由图5可知,XFEM分析所得的面板-U肋焊缝断裂寿命与试验结果误差小于3%,所预测的裂纹萌生寿命与试验结果误差也在10%之内。表明基于 XFEM 的有限元分析方法可以较精确地预测面板与 U 肋焊缝疲劳细节的裂纹扩展路径、疲劳裂纹的萌生寿命及断裂寿命。

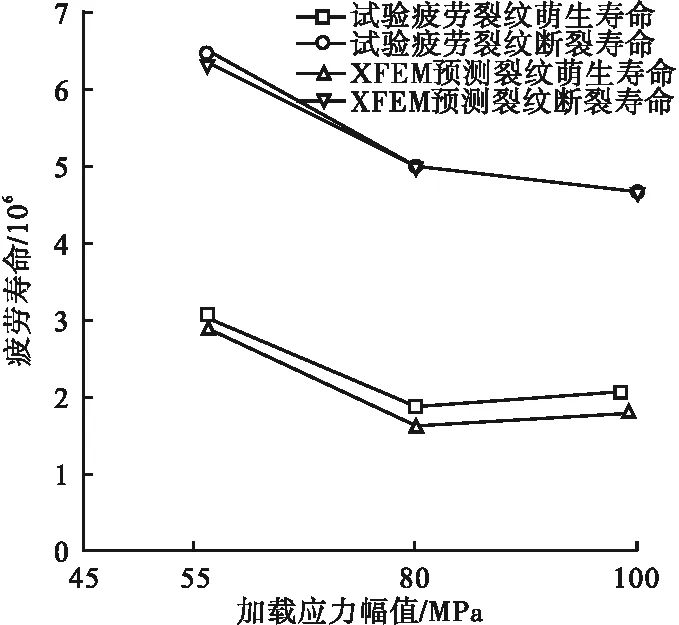
图5 XFEM与试验疲劳寿命Fig.5 Comparison of fatigue life between XFEM and test

2 面板-U肋焊缝疲劳裂纹扩展研究

2.1 正交异性板XFEM有限元模型

正交异性板纵、横肋布置较为密集,因此其受载后具体疲劳细节处的应力影响线通常较短。其中,纵向影响线约为3 000 mm,横向影响线约为750 mm。考虑车辆轴距往往大于该影响区域,因此在建立模型时通常可忽略车辆数量及车辆轴距的影响[11-12]。笔者基于国内某钢桥正交异性板的构造尺寸,建立以横桥向为X方向、U肋高度的方向为Y方向的三U肋正交异性板二维有限元模型(见图6)。模型选用的材料属性及网格划分与1.1节中相同。加载时,在顶板两侧约束X方向和Y方向的刚性位移条件,即Ux=0,Uy=0。

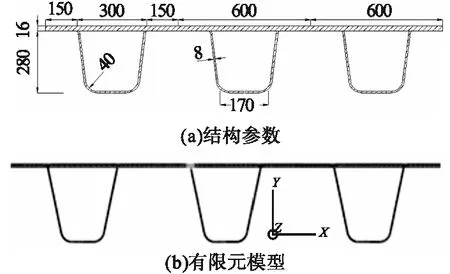
图6 三U肋有限元分析模型Fig.6 Three U-rib FEA model

2.2 加载工况

加载制度参考《公路钢结构桥梁设计规范》(JTG D64—2015)规定[13]:桥面系构件疲劳分析时采用如图7所示的疲劳荷载计算模型Ⅲ。基于建立有限元模型的结构尺寸与正交异性板的受力状态,笔者选取长×宽为600 mm×200 mm,轴重为60 kN的一侧单轮作为疲劳荷载,同时选取应力比为R=0.1的正弦曲线作为加载频率。

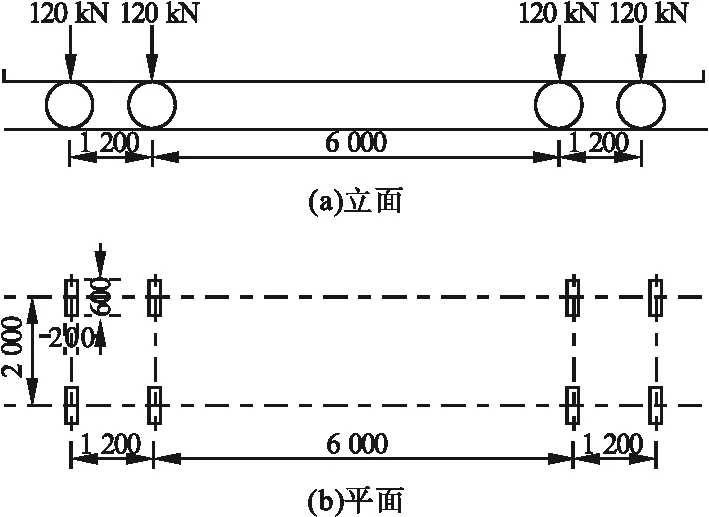
图7 Ⅲ型疲劳荷载立面、平面参数Fig.7 Elevation and plane dimensions of type Ⅲ fatigue load

由于轮载的横桥向作用位置对正交异性板构造细节的应力循环特征有显著的影响,为了确定最不利的加载位置,笔者考虑轮载的最大横向分布概率,确定了如图8所示的三种加载工况,即轮载中心分别作用于U肋上方(工况一)、U肋腹板上方(工况二)及U肋肋间(工况三)。基于建立的有限元模型,分别计算三种工况下正交异性板的受力状态。三种工况下U2肋与面板焊缝焊趾处应力和位移影响线如图9所示。由图可知,在工况一、工况二、工况三加载下,关注位置处的最大应力分别为28.3 MPa、28.1 MPa、24.3 MPa,竖向最大位移分别为4.77 mm、4.69 mm、4.07 mm。因此,在以U2肋与面板焊缝位置为关注位置时,最不利的加载位置为U肋正上方(工况一)。

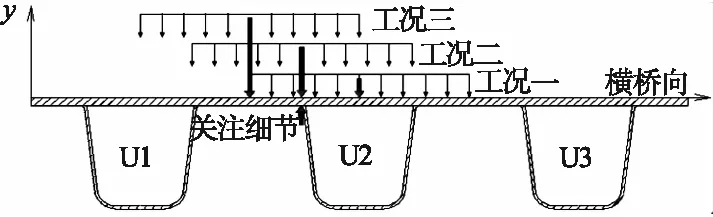
图8 横桥向加载工况Fig.8 Transverse loading conditions

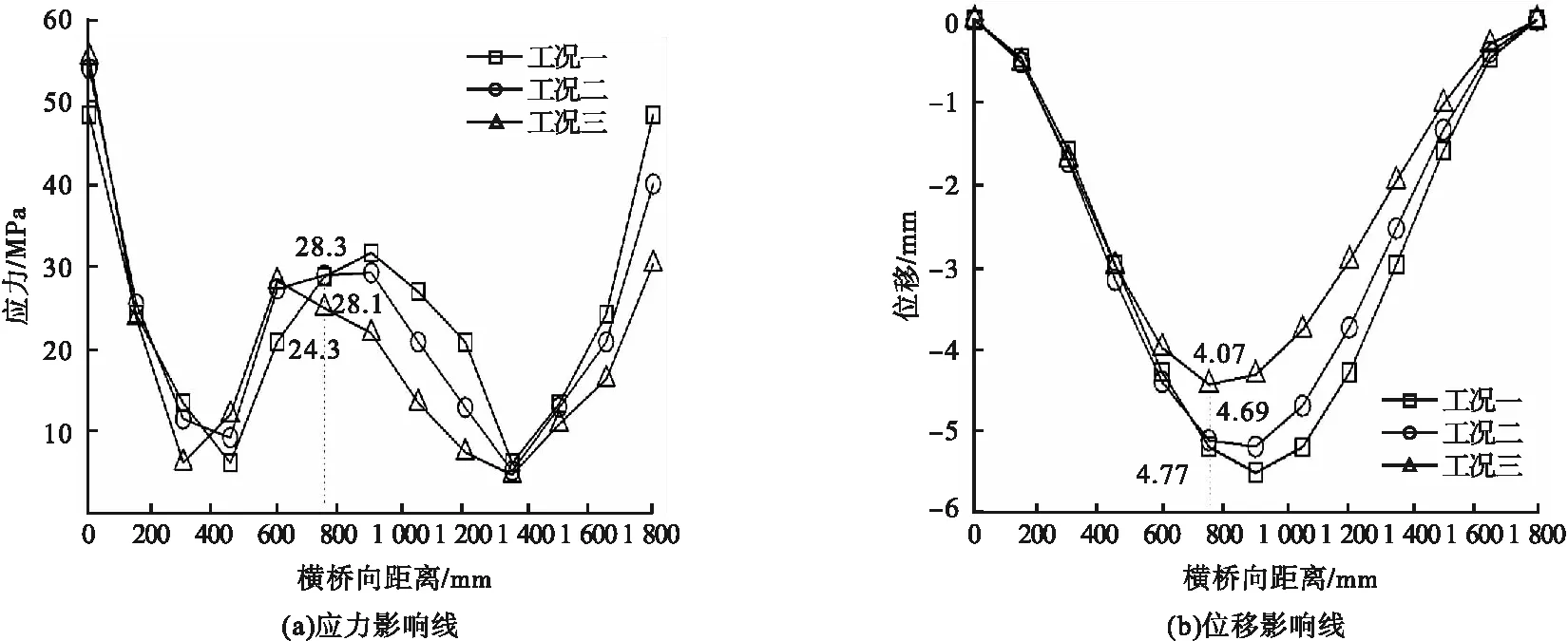
图9 横桥向应力及变形影响线Fig.9 Stress and deformation influence lines of transverse bridge direction

2.3 裂纹扩展

在面板-U肋焊缝的焊趾、焊跟处分别预设长度为1 mm的初始裂纹(见图10),并通过有限元分析得到焊趾、焊跟处的裂纹扩展路径、裂纹扩展速率及应变能释放率,结果分别如图11、图12和图13所示。

图10 焊趾、焊跟处预设1 mm初始裂纹Fig.10 1 mm initial crack at the weld toe and heel

图11 焊趾、焊跟疲劳裂纹扩展路径Fig.11 Crack propagation path at weld toe and root

图12 焊缝裂纹扩展速率曲线Fig.12 Weld crack propagation rate curves

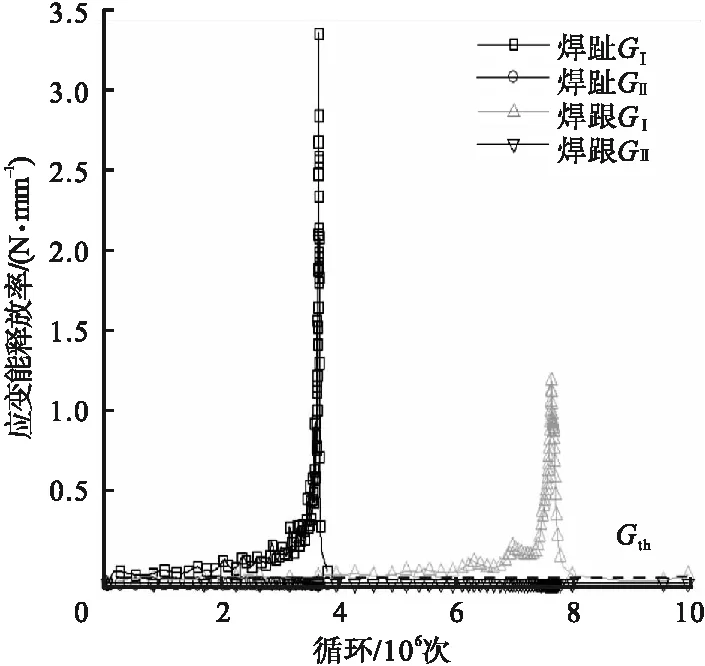
图13 焊缝裂纹应变能释放率曲线Fig.13 Strain energy release rate curves of weld crack

由图11可知,焊趾、焊跟处疲劳裂纹以接近垂直于板厚方向向顶部扩展,当疲劳荷载加载到362万次时,焊趾处裂缝长度达到70%的面板厚度即11.2 mm;当疲劳荷载加载到763万次时,焊跟处裂缝长度达到11.2 mm。

由图12可知,焊趾处疲劳裂纹的扩展速率显著大于焊跟处。此外,依据面板70%厚度的失效标准,计算焊趾的疲劳寿命N为362万次、焊跟处疲劳寿命N为763万次。可见,焊跟处抗疲劳性能要优于焊趾,这一结果与文献[14]中在面板-U肋部分熔透焊缝细节疲劳破坏试验所观察到的最易开裂位置一致。

由图13可知,面板与U肋焊缝细节焊趾、焊跟处的疲劳裂纹均是以Ⅰ型张拉裂纹为主导的Ⅰ-Ⅱ型混合裂纹。当GⅠ大于应变能释放率阈值Gth时,裂纹开始扩展;焊趾、焊跟处的裂纹分别扩展至13.2 mm、11.5 mm时,GⅠ达到峰值,此厚度约为面板厚度的72%～82%。这表明裂纹扩展临界长度取70%的钢板厚度是偏于安全的,GⅡ值则普遍小于应变能释放率阈值Gth,几乎可以忽略不计,GⅠ约为GⅡ的数百至数千倍,表明GⅠ是控制疲劳裂纹扩展的关键参数。

3 疲劳裂纹扩展影响因素分析

基于能量准则的Paris公式为

(1)

式中:a为裂纹长度;N为寿命;C3、C4为材料参数;ΔG为应变能释放率幅值。

对式(1)取积分可得疲劳寿命为

(2)

由式(2)可知,影响钢桥面板-U肋焊缝细节疲劳裂纹扩展的因素有初始裂纹长度a0、面板厚度h、应力比R等。笔者基于建立的有限元模型及加载制度,进一步分析各因素对焊跟及焊趾处裂纹扩展速率及其疲劳寿命的影响。

3.1 初始裂纹长度

大量钢桥面板焊接节点疲劳试验研究表明,初始焊接缺陷导致的疲劳抗力劣化效应是决定钢桥面板焊接细节疲劳性能的关键因素[2-3]。因此,在疲劳性能的研究中,对初始裂纹长度的选取十分重要。笔者在焊跟和焊趾处分别预设了六种初始裂纹长度a0,分别为0.50 mm、0.65 mm、0.80 mm、1.00 mm、1.20 mm、1.50 mm。

不同初始裂纹长度下,焊跟和焊趾处的裂纹扩展速率如图14所示。由图可知,随初始裂纹长度增加,焊趾和焊跟处的裂纹扩展速率显著提升。值得注意的是,初始裂纹主要是影响疲劳裂纹前期的扩展速率,对后期并无较大影响。说明随初始裂纹减小,焊趾和焊跟处疲劳寿命会明显提高。因此,在工程中严控制初始焊接缺陷是提高钢桥疲劳性能的有效途径[15]。

图14 裂纹扩展速率随初始裂纹长度变化曲线Fig.14 Curves of crack growth rate with different initial crack length

当裂纹扩展至面板厚度70%时,焊趾、焊跟的疲劳寿命如图15所示。对比初始裂纹长度为0.50 mm时的疲劳寿命,当初始裂纹长度分别为0.65mm、0.80 mm、1.00 mm、1.20 mm及1.50 mm时,焊趾处的疲劳寿命分别减少了7.87%、20.3%、29.7%、37.6%、46.6%,焊跟处的疲劳寿命也分别减少了14.55%、31.4%、41.8%、42%、51.2%。由此可知,随初始裂纹长度的增加,面板与U肋焊缝的疲劳寿命会显著下降。

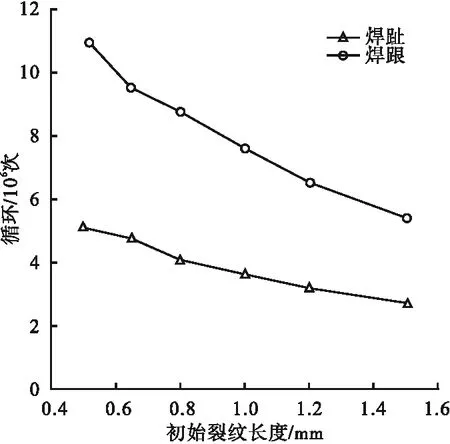
图15 不同初始裂纹长度下的断裂寿命Fig.15 Failure life under different initial crack length

3.2 面板厚度

面板-U肋采用部分熔透焊接时,面板厚度会对焊缝细节的疲劳性能产生较大影响[16-17]。本节在焊趾及焊跟处预设1 mm的初始裂纹,面板厚度h分别选取为14 mm、16 mm、18 mm和20 mm,分析板厚对其疲劳性能的影响。

焊趾及焊跟在不同面板厚度下的裂纹扩展速率如图16所示。由图可知,增加面板厚度,焊趾和焊跟处的裂纹扩展速率会明显降低:适当加厚面板厚度,有利于抑制疲劳裂纹扩展。板厚为14 mm、16 mm、18 mm和20 mm时,焊趾及焊跟的疲劳寿命如图17所示。相较于面板厚度14 mm时的疲劳寿命,其他三种厚度下焊趾的疲劳寿命分别提高了133%、403%、797%,焊跟的疲劳寿命也分别提高了72%、199%、425%。但在工程中,增加板厚提高疲劳性能时,应充分考虑板厚对焊接性能的影响及钢材的“板厚效应”。

图16 裂纹扩展速率随面板厚度变化曲线Fig.16 Curves of crack growth rate with panel thickness

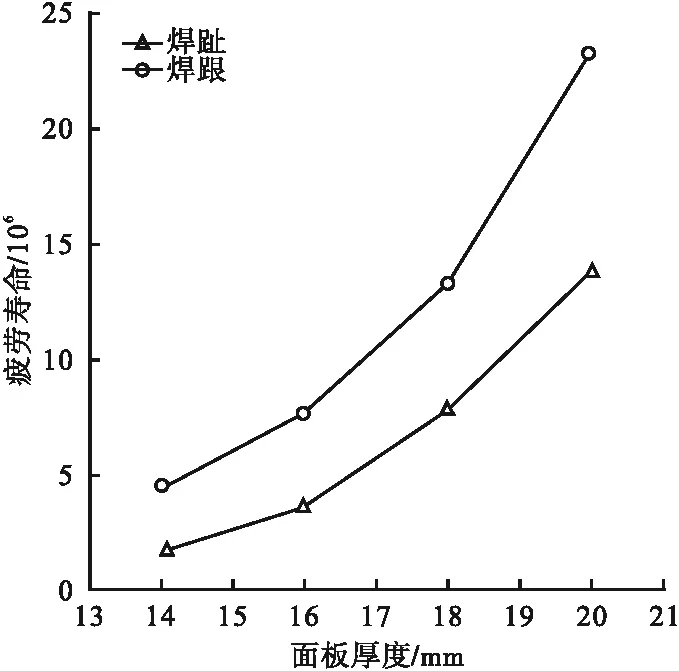
图17 不同面板厚度情况下疲劳寿命变化趋势Fig.17 Variation trend of fatigue life under different panel thickness

3.3 应力比

笔者分别考虑应力比R为0.1、0.3、0.5、0.8对正交异性板面板-U肋焊缝疲劳性能的影响[18-21]。图18为有限元分析所得的不同应力比下焊趾及焊跟的裂纹扩展速率。由图可知,以应力比R=0.5为界限,当应力比小于界限值时,焊趾及焊跟的裂纹扩展速率较快,且随应力比增加,裂纹扩展速率仅略有降低;但是,当应力比大于界限值时,焊趾及焊跟的裂纹扩展速率大幅降低,且对裂纹扩展表现出明显的抑制作用。

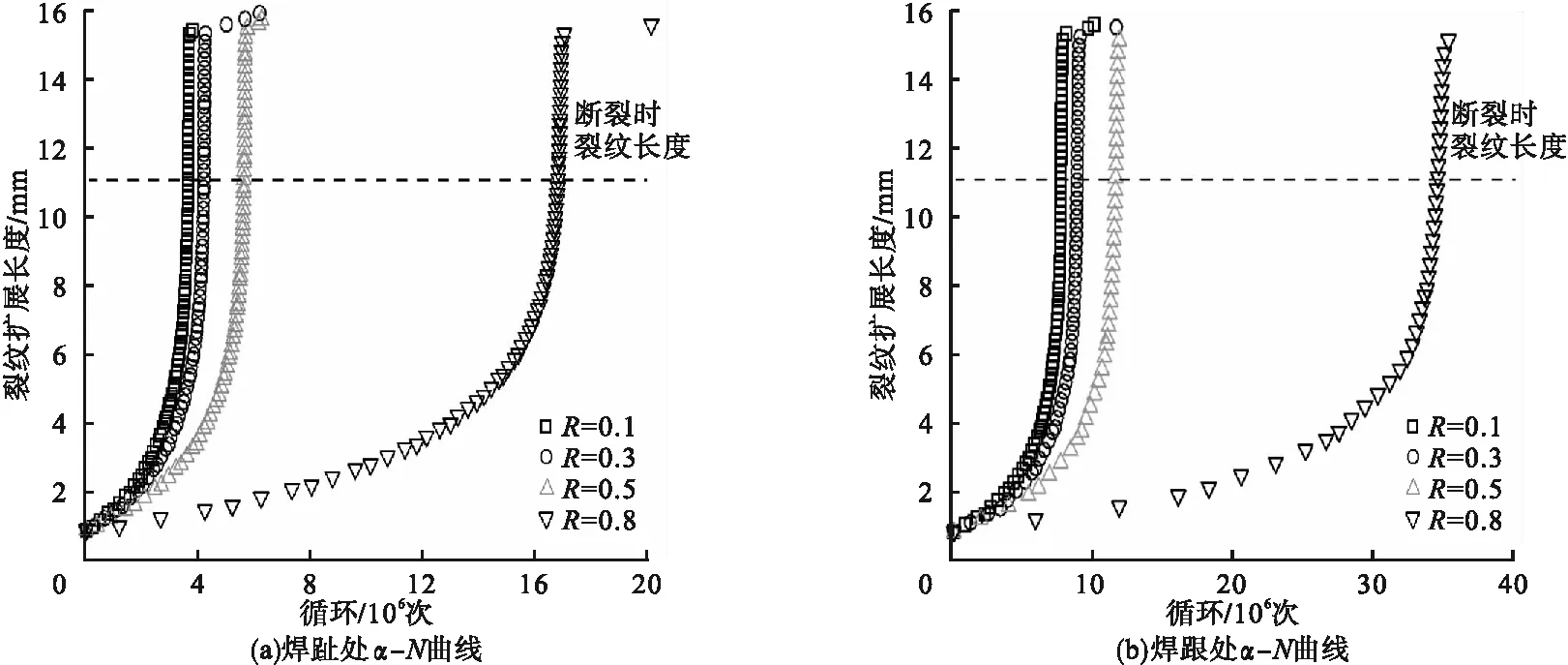
图18 裂纹扩展速率随应力比变化曲线Fig.18 Curves of crack growth rate with different stress ratio

裂纹扩展至面板临界厚度时,焊趾及焊跟的疲劳寿命如图19所示。由图可知,与裂纹扩展规律相似:当应力比小于临界应力比时,随应力比增加,焊趾及焊跟处的疲劳寿命略有增加;但当应力比大于临界应力比时,增加应力比,焊趾及焊跟处的疲劳寿命会显著提升。

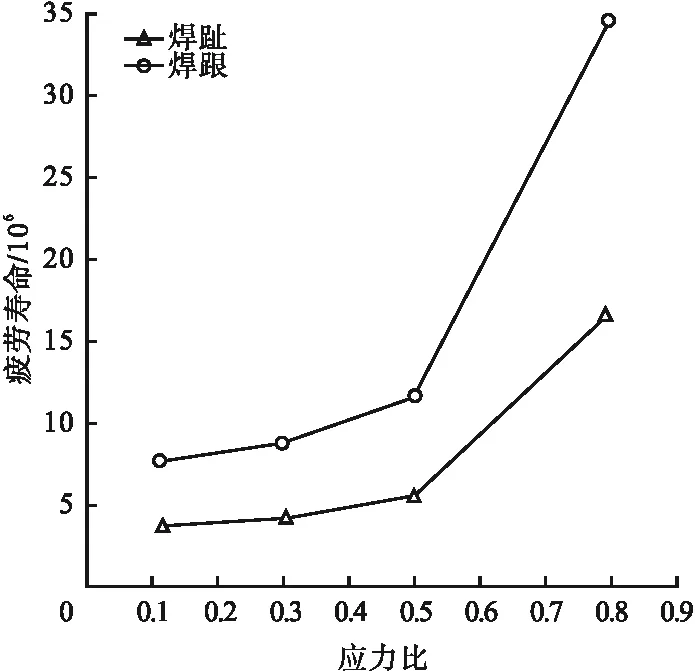
图19 不同应力比情况下疲劳寿命变化趋势Fig.19 Variation trend of fatigue life under different stress ratio

4 结 论

(1)基于断裂力学的扩展有限单元法能较为精准地预测顶板-U肋焊缝细节的疲劳裂纹扩展路径、疲劳裂纹的萌生寿命及断裂寿命。

(2)对于正交异性板面板与U肋焊缝细节,焊趾处裂纹扩展速率显著快于焊跟处,且焊趾的疲劳寿命显著低于焊跟处,说明源于焊趾处的疲劳裂纹更危险。

(3)正交异性板面板-U肋焊缝疲劳裂纹是以Ⅰ型裂纹为主导的Ⅰ-Ⅱ混合型裂纹,裂纹扩展方向主要取决于Ⅰ型裂纹应变能释放率。

(4)对面板-U肋焊缝细节,初始裂纹长度越大、面板厚度越小、应力比越小,其疲劳裂纹的扩展速率愈快、疲劳寿命相应减小,反之,则疲劳裂纹的扩展速率愈慢,有利于提升该细节处的疲劳寿命。