近零能耗建筑围护结构多目标优化研究

冯国会,陈 菲,常莎莎

(沈阳建筑大学市政与环境工程学院,辽宁 沈阳 110168)

目前,建筑能耗占全社会总能耗的比重约为40%,建筑能源消耗强度高、碳排放量大。在建筑运营阶段,碳排放在全社会总碳排放量中所占的比重达到了22%[1-3]。近零能耗建筑的发展对降低能源消耗、减少碳排放、保护环境有着促进作用。N.Abdou等[4]对摩洛哥六个气候区建筑进行改造,使其满足近零能耗建筑的要求,找到同时满足建筑生命周期成本、节能和热舒适的最佳解决方案,借助MOBO优化工具与TRNSYS软件联合使用,对建筑朝向、窗型、窗墙比、墙体和屋面的保温渗水率等进行了多目标优化。M.Fesanghary等[5]提出了一种基于和声搜索算法的多目标优化模型,使生命周期成本和碳排放量最小化,以找到一种最佳的建筑围护结构组合。霍海娥等[6]在成都某既有建筑墙体的节能改造设计中,建立了数值计算法和多目标遗传算法NSGA-II的优化模型,对墙体单位面积的年总能耗和保温材料的成本进行优化。余镇雨等[7]将MATLAB和TRNSYS能耗模拟软件联合运行,对近零能耗建筑全生命期的运行一次能耗和全生命期成本进行多目标优化,给出了不同气候区典型城市多目标优化均衡解。国内外学者虽已开展近零能耗建筑和可持续建筑的多目标优化设计研究,但研究中同时考虑建筑能耗全生命周期碳排放和经济性的三目标优化设计研究较少。

因此,笔者以沈阳市某一近零能耗示范建筑为例建立模型,基于对近零能耗建筑的全生命周期运行能耗、碳排放以及成本进行多目标、多参数的优化研究,利用NSGA-Ⅱ遗传算法,并使用MOBO优化工具和EnergyPlus模拟软件耦合模拟计算;再利用加权和法通过给目标函数分配不同的权重因子来线性量化转换成单目标问题,以得到多目标问题的最优解。

1 多目标优化方法

1.1 NSGA-Ⅱ遗传算法

NSGA-II算法是在多个优化目标的约束下,逐步在帕累托前沿解的方向上进行优化,通过多代的遗传操作,算法能够自动进行设计方案的空间搜索和优化,尝试不同的设计决策,不断细化建筑设计方案,并逐步到达帕累托前沿解。该算法能够有效地避免设计方案陷入局部最优状态,实现全局最优果[12]。

1.2 MOBO优化平台

MOBO软件可处理具有连续变量和离散变量的单目标和多目标优化问题,可以自动改变需要优化的参数,实现迭代操作过程。通过对连续变量和离散变量数量的函数的关系来进行评估,选择适当的算法和参数,如表1所示。

表1 NSGA-II遗传算法相关参数Table 1 NSGA-II genetic algorithmparameters

整个搜索空间仅通过6×150=900个建筑围护结构参数配置来迭代计算,避免计算次数过多,节省了大量时间。

1.3 目标函数

多目标优化问题是研究多个目标函数(n≥2)在满足一定约束条件下实现最优化的问题,其数学模型描述:

Min {F1(x),F2(x),F3(x)}.

(1)

式中:F1,F2,F3为目标函数,x=[x1,x2,…,xn]。

第一个函数(F1)为全生命周期建筑运行能耗,定义为建筑采暖能耗、制冷能耗、设备能耗之和。在建筑的全生命周期内,建筑使用阶段的能耗占90%以上,因此能耗计算限定于建筑的使用阶段。建筑照明能耗、生活热水能耗不受优化变量影响,因此不考虑在内,同样也没有考虑这部分的碳排放和成本。其计算式可表示为

E=n×(Eh+Ec+Ee).

(2)

式中:Eh为建筑年供暖能耗,J;Ec为建筑年制冷能耗,J;Ee为建筑年均设备能耗,J;n为建筑设计使用寿命,取50 a。

第二个函数(F2)为全生命周期碳排放量,包括生产阶段碳排放和运行阶段碳排放,采用排放因子法进行计算,即按照每个阶段碳的来源,整理出碳排放清单,然后将数据和与其对应的碳排放因子相乘即为某一排放渠道的碳排放量[10]。电力碳排放系数采用东北电网平均碳排放因子0.776 9 kg CO2/(kWh),建筑使用寿命取50 a。其计算式可表示为

LCCE=Cp+Cr.

(3)

Cp=∑δiηiβiAi.

(4)

Cr=EβCen.

(5)

式中:Cp为建材生产阶段碳排放量,kg;Cr为建筑运行阶段碳排放量,kg;δi为第i种材料的厚度,m;ηi为第i种材料的密度,kg/m3;βi为第i种材料的碳排放系数;A为各围护结构的面积,m2;E为建筑供暖空调年耗电量,J;βe为电力碳排放系数。

第三个函数(F3)为全生命周期成本,包括建筑初投资及全生命周期内运行费用折合成现值的总和[8]。对于建筑围护结构的优化设计,建筑初投资只计算了建筑围护结构生产阶段所用到的建材成本。运行阶段是全生命期内空调系统、设备系统的运行费用折合成现值的总和。其计算式[7]可表示为

LCC=TCi+TCo.

(6)

TCi=∑φi×Mi.

(7)

(8)

r=(R-e)/(1+e).

(9)

式中:TCi为初投资成本,元/m2;TCo为使用阶段成本,元/m2;φi为第i种材料的单价,元/m2;Mi为第i种材料的消耗量,m3;Ei为建筑供暖空调年耗电量,(kW·h)/m2;Pe为电价,元/(kW·h);r为贴现率;R为名义利率,取0.07;e为能源价格增长率,取0.02。n为建筑设计使用寿命,取50 a。

1.4 目标优选

在实际应用中,通过多目标优化计算可以筛选出一系列最优解方案,如何进行寻优是关键,最优解的选择主要取决于设计者自身或者其研究目的。为了从Pareto解中确定多目标优化问题的最优解,采用加权和法,将多准则优化问题转化为单准则优化问题,通过为对目标赋予权重系数,构建新的目标函数,以得到不同决策重心下的参数组合。函数定义为

Min[u(F1(x),F2(x))]=

(10)

式中:Fi min和Fi max分别为第i个目标函数的最大值和最小值;w1、w2为反映目标函数相对重要性的权重系数;∑wi必须等于1,在无偏好的情况下,对标准化处理后的目标函数平均分配权重。

使用节能率(ESR)、碳排放量节约率(CESR)、成本节约率(CSR)与建筑初始值进行比较,以评价确定的最优解[4],公式如下:

ESR=1-(F1opt/F1bc).

(11)

CESR=1-(F2opt/F2bc).

(12)

CSR=1-(F3opt/F3bc).

(13)

式中:Fopt为最优解的目标函数值;Fbc为建筑初始目标函数值。

2 多目标优化模型

2.1 模型建立

以沈阳建筑大学近零能耗示范建筑为例,根据设计图纸基础信息,对建筑平面、外立面及屋顶样式进行了适当简化,借助OpenStudio软件建立基准模型。该建筑能源供应系统以地源热泵为主,以太阳能供热系统为辅。由于EnergyPlus是通过热工区域来模拟建筑能耗,因此将该两层建筑分为10个热区(见图1)。

图1 建筑热工分区图Fig.1 Thermal zoning of the building

2.2 气候参数

案例建筑所处地区辽宁省沈阳市,年平均气温为14.6 ℃,年太阳总辐射量为2 262.84 W/m2。按现行标准《公共建筑节能设计标准》(GB50189—2015)[15],该建筑处在严寒C区,冬季室内计算温度设定为20 ℃,夏季室内计算温度为26 ℃。

2.3 决策变量

通过对近零能耗建筑围护结构影响因素的调查分析后,选取5种围护结构,共7个变量参数,包括外墙保温层厚度、屋面保温层厚度、地面保温层厚度、Low-e窗户参数(外层玻璃厚度、中间层玻璃厚度和玻璃间距)以及保温材料类型。表2列出了建筑围护结构的输入参数以及参数初始值和变化范围,其中外墙、屋面、地面保温层厚度为连续变量,玻璃厚度和玻璃间距为离散变量,而不同类型的保温材料会有不同的传热系数、密度及比热,需要改变的参数过多,因此无法同时模拟,其优化结果单独列出。聚苯板(EPS)、挤塑板(XPS)、聚氨酯(PU)三种保温材料的导热系数分别为0.033 W/(m·K)、0.028 W/(m·K)、0.023 W/(m·K)。

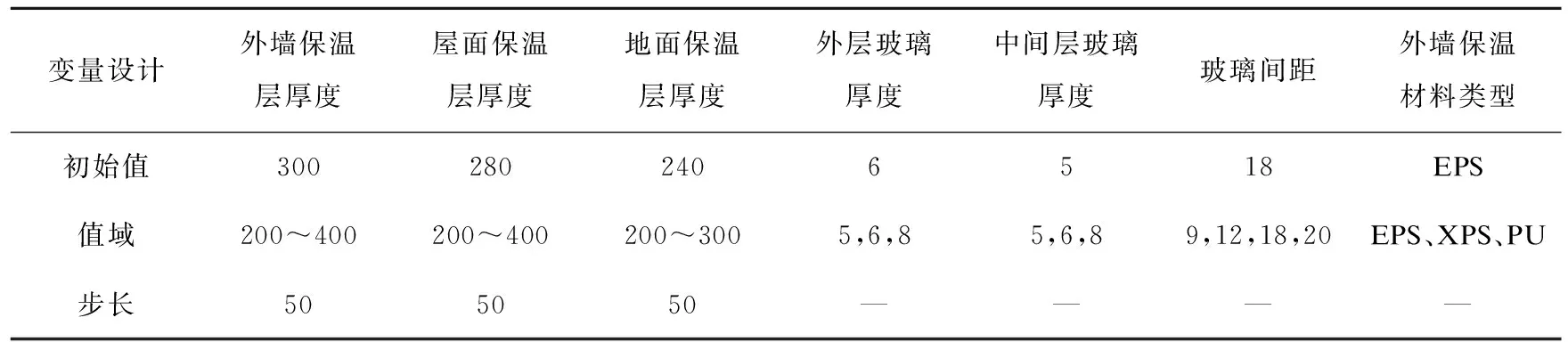
表2 优化变量的相关参数设定Table 2 Relevant parameter settings of optimization variables mm

3 多目标优化结果与分析

3.1 双目标对比分析

多目标优化的解决方案并不唯一,而是给出一组折中的权衡解决方案,称为帕累托前沿解。对建筑能耗、碳排放及成本三个目标函数两两组合,进行对比分析,得出建筑能耗-成本、碳排放-能耗、碳排放-成本的寻优结果(见图2～图4)。

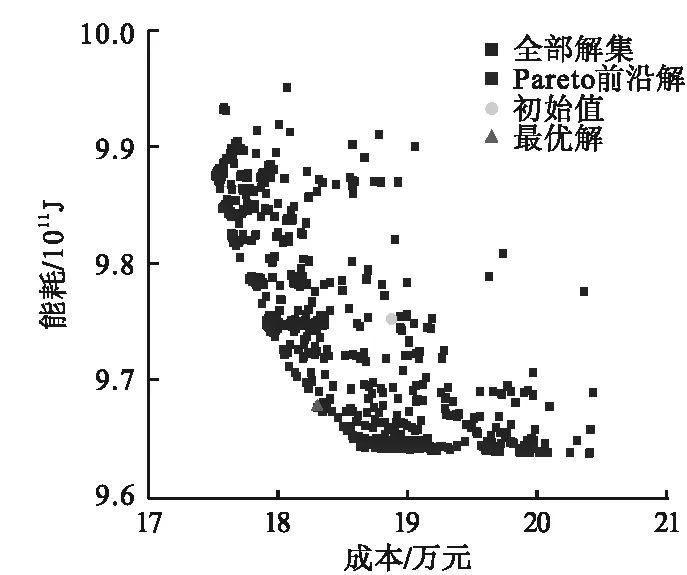
图2 能耗-成本目标优化结果Fig.2 Target optimization results ofenergy-cost

由图2可以看出,全生命周期能耗及成本两个目标函数之间呈帕累托分布,结果呈反比。随着成本的增加,能耗呈下降趋势,原因是决策变量的改变与成本直接相关。采用保温性能一般的墙体虽然会降低建筑成本,但是建筑能耗必然会增大。

图3中,全生命周期碳排放和能耗两个目标函数之间也呈帕累托分布,但是随着能耗的增加,碳排放量有小范围增加,因运行能耗的增加导致运行阶段的碳排放量也随之增加。

图3 碳排放量-能耗目标优化结果Fig.3 Target optimization results of carbon emissions-energy consumption

图4中,由于全生命周期碳排放和成本目标函数使用相似公式进行评估,因此两目标并不是冲突目标,结果并未获得帕累托分布,所寻的最优解也是互相重叠,趋近于极值点。

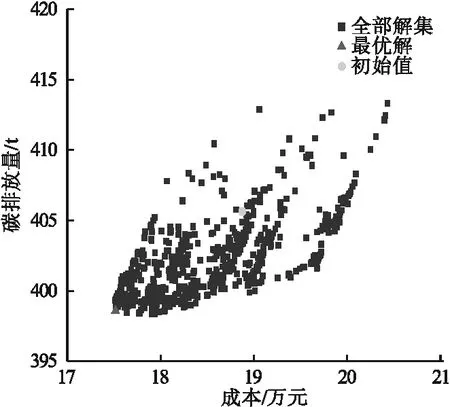
图4 碳排放量-成本目标优化结果Fig.4 Target optimization results ofcarbon emissions-cost

3.2 三目标优化结果分析

为了实现近零能耗建筑的低能耗、低成本以及低碳排量,将三个目标最小化的多目标优化结果如图5所示。目标函数增加到了3个,因此此时的帕累托前沿解将不再是一条曲线,而是一个曲面,筛选出的最优解均分布在帕累托前沿上。

加权和法除了筛选出的最优解,另外分别给出了能源最优、低碳最优、成本最优时的情况,分别与案例建筑初始性能进行比较。

表3为近零能耗建筑围护结构优化结果。从表3中可以看出,最优解相对于初始状态来说,外墙保温层厚度增加了40 mm,屋顶保温层厚度减少了80 mm,地面保温层厚度减少了40 mm,外层玻璃厚度减少了1 mm,中间层玻璃厚度增加了3 mm,玻璃间距不变。与建筑初始状态相比,最优解下的建筑能耗、碳排放量及成本均有降低。

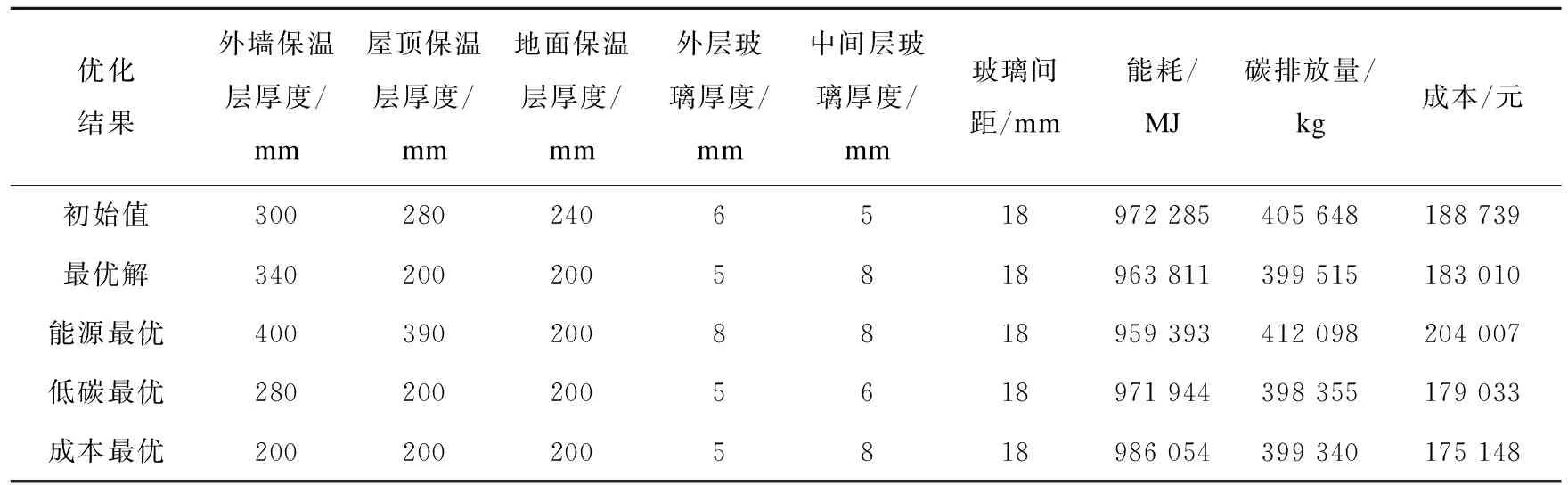
表3 近零能耗建筑围护结构优化结果Table 3 Optimization results of building envelope structure of near zero energy consumption

对近零能耗建筑各优化结果进行ESR、CESR、CSR三目标评估(见图6),从图6中可以看出,优化后的建筑围护结构与初始状态相比得到了改进。在最优解下,建筑的节能率为0.87%,全生命周期碳排放节约率为1.51%,全生命周期成本节约率为3.04%。能源最优的情况下,节能率为1.33%,但是全生命周期碳排放节约率和全生命周期成本节约率却是-1.59%和-8.09%,说明当优先降低能耗时碳排放和成本均增加,此时外墙保温层厚度达到了400 mm,在节能的同时,成本大幅度增加。在低碳最优的情况下,节能率为0.04%,全生命周期碳排放节约率为1.80%,全生命周期成本节约率为5.14%。在成本最优的情况下,节能率为-1.42%,全生命周期碳排放节约率为1.56%,全生命周期成本节约率为7.20%。采用加权和法确定的最优解能兼顾建筑的节能性、成本性和环保性,单项最优解却有一定的局限性,在优化某一个目标时可能会导致其他目标不尽如人意。

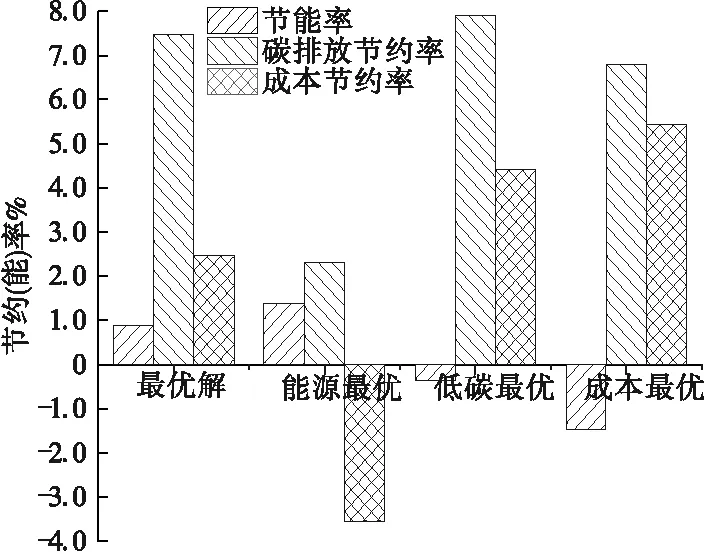
图6 优化后近零能耗建筑三目标评估结果Fig.6 Three objective evaluation of net zero energy building after optimization

3.3 外墙保温材料类型的影响结果

在非透明围护结构中,外墙所占的热损失比例是最高的,因此,近零能耗建筑围护结构一般采用保温性能高的保温材料,能耗虽然降低,但也会相应增加建筑碳排放以及建筑的初始成本。选择3种常用建筑外墙保温层材料,进一步分析建筑的各方面性能。通过多目标优化模拟计算得到的一系列解集(见图7)。最优解A,B,C分别为当建筑外墙保温层材料为EPS,XPS,PU时对应的最优结果。

图7 外墙保温材料的三目标优化结果Fig.7 Three objective optimization results of exterior wall insulation materials

表4为不同外墙保温材料类型围护结构的优化结果。建筑外墙初始保温层材料为EPS,由表4可以看出,相较于选择EPS,选择XPS为保温材料时,外墙保温层厚度减少130 mm,中间层玻璃厚度减少3 mm;选择PU为保温层材料时,外墙保温层厚度减少120 mm,中间层玻璃厚度减少2 mm。但是相应的,其能耗及碳排放均有不同程度增加。

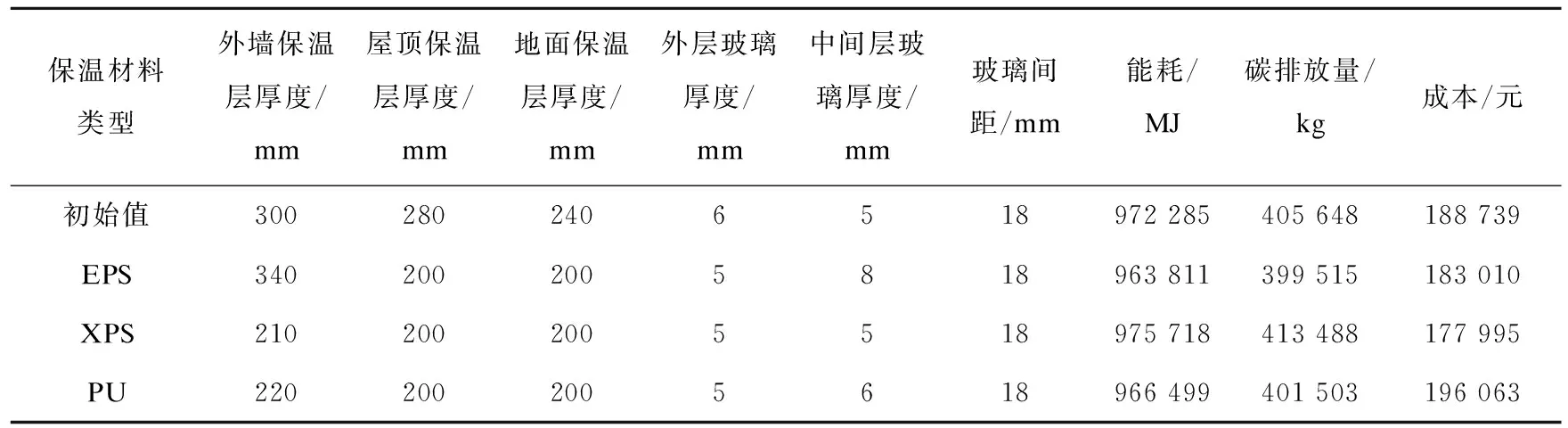
表4 不同外墙保温材料类型围护结构优化结果Table 4 Optimization results of envelope structure with different types of external wall insulation materials

更改外墙材料参数后,对建筑进行三目标函数评估(见图8),由图8可看出,与建筑初始状态比较,当外墙保温层类型为EPS时,建筑的节能率和碳排放节约率均为最高,分别为0.87%和1.51%,成本节约率为3.04%;当外墙保温层类型为XPS时,建筑节能率为0.35%,碳排放节约率为-1.93%,成本节约率为5.69%,虽然建筑成本有所减少,但是能耗变化不明显,并且增加了建筑的碳排放;当外墙保温层类型为PU时,建筑节能率为0.60%,碳排放节约率为1.02%,成本节约率为-3.88%。由此可见,当同时考虑建筑能耗、碳排放及成本时,EPS外墙保温材料为最优。

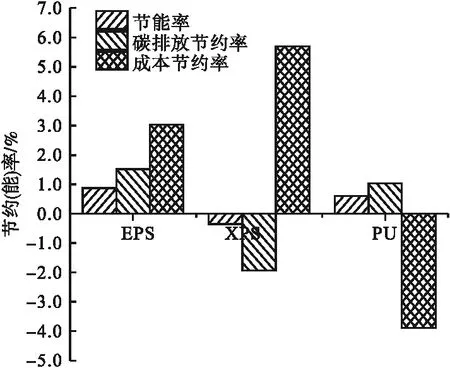
图8 不同材料类型的三目标评估结果Fig.8 Three objective evaluation of different material types

4 结 论

(1)通过对不同类型保温材料分析,综合考虑建筑能耗、碳排放等多个目标,外墙保温层类型为EPS时,建筑的节能率和碳排放节约率均为最高。与初始状态相比,三个目标均得到了改进,最优解下净零能耗建筑节能率、碳排放节约率和成本节约率分别为0.87%、1.51%和3.04%。

(2)近零能耗建筑围护结构参数最佳组合为外墙保温层厚度340 mm、屋顶保温层厚度200 mm,地面保温层厚度200 mm、外层玻璃厚度6 mm,中间层玻璃厚度5 mm、玻璃间距18 mm。