布袋注浆桩复合地基固结方程解析解

彭仪普,汤致远,邓湘洋,李 剑,李子超

(中南大学土木工程学院,湖南 长沙 410075)

在我国东部沿海部分地区,地貌表现为全新世晚期滨海淤积平原地貌,该地区土体性质较差,均为软土地基。目前常用的地基处理方法有换填、强夯等加固天然地基处理方式和水泥搅拌桩等置换处理方式。基于软土特性,这些地基处理方式存在适用性差、效果不明显的特点。而通过土工织物袋或尼龙袋以及水泥等注浆液形成柱状或葫芦状硬化体挤密加固土体的软土地基处理方法受到越来越多的关注。

布袋桩由于布袋排水特性可以加快土体固结,缩短工期[1],就复合地基固结理论,诸多学者对其进行了研究。1948年,R.A.Barron[2]提出了砂井地基径向轴对称固结理论,后续学者不断对Barron固结理论中的假定进行修正,极大促进了砂井地基固结理论的研究。杨涛等[3]将整个复合地基视为均质的复合材料,采用复合模量法对荷载瞬时施加和单级施加的黏结材料桩复合地基线弹性固结理论进行了研究。谢康和等[4-5]通过两种不同的方法对复合地基固结模型进行了修正。部分学者对考虑桩体和土体发生二维变形情况下的固结理论进行了研究[6-8]。T.Yang等[9]在卢萌盟等[10-11]提出的轴对称固结模型的基础上,进一步提出未打穿不透水桩复合地基的固结解析解,使对不透水桩复合地基固结问题的研究又得以拓展。D.W.Zhang等[12]按照渗透系数将塑料排水板和土体等效为均质土体,利用K.Terzaghi[13]提出的天然地基一维固结模型计算组合桩复合地基固结度。陈蕾等[14]利用砂井地基理论研究了组合桩复合地基固结问题。

以上学者采用理论分析和试验等方法对复合地基固结理论进行了深入研究,促进了对复合地基固结理论的认识和了解,然而其理论研究大多是基于一定的条件假设及模型简化,对更为复杂的情况只能通过数值求解的方法进行计算。基于此,笔者针对布袋注浆桩特性,考虑土体水平渗透系数的三种模式以及附加应力延深度的非均匀分布,首次推导布袋注浆桩复合地基固结控制方程,并求出在不同加载情况下的固结解析解,为软土地基处理的设计计算方法提供参考。

1 固结控制方程推导

布袋注浆桩复合地基在正方形布桩时,为方便计算,参照碎石桩复合地基,布袋注浆桩复合地基单桩分担地处理地基面积的等效圆直径de=1.13s,其中s为复合地基桩间距(见图1)。

图1 布袋桩复合地基布桩图Fig.1 Pile layout of bag pile composite foundation

1.1 基本假定

笔者以轴对称固结模型为基础[11],桩周土体存在竖向水流,并考虑土体的水平向渗透系数,且水平向渗透系数沿径向发生变化。由于布袋注浆桩其特有属性,桩体为不排水且桩-布袋边界为不排水边界,布袋-土界面为弱排水界面,所取单元的径向外边界即影响区边界为不排水界面。

考虑到现场环境的复杂性,采用固结简化模型(见图2),基于以下假定:

图2 布袋注浆桩复合地基固结模型Fig.2 Consolidation model of composite foundation with cloth bag-grouting-pile

①桩体为不透水桩,桩体内不存在超静孔隙水压力;

②布袋注浆桩所采用布袋的水平渗透系数和竖直渗透系数不变,分别为khb和kvb;

③等应变条件成立,即桩体、布袋和土体均受侧向约束,并且竖向变形相等;

④无竖向压力作用时,常仕维等[15-17]运用修正的达西定律去描述土工织物的渗透特性,认为当流速较小时,水流进入孔隙或从孔隙流出时产生的局部水头损失相对于水流通过由织物形成的孔隙时产生的水头损失可以忽略,表现为层流。因此假定复合地基内水的渗流和流动符合Darcy定律;

⑤外部荷载在地基中引起的平均附加应力σ(z,t)为深度与时间的函数。

1.2 推导过程

笔者在进行布袋注浆桩复合地基固结控制方程推导时考虑扰动效应(涂抹效应),将桩周土分为扰动区和未扰动区,并假定扰动区土体的渗透系数小于未扰动区土体,且布袋的水平渗透系数和竖直渗透系数不变,分别为khb和kvb。根据扰动区土体渗透系数随位置变化模式的不同,考虑扰动效应的方法主要包括模式一、模式二、模式三(见图3)。模式一:假定扰动区土体渗透系数保持不变,此模式为最早考虑扰动效应,造成的误差较大,适用于扰动区较小的情况;模式二:假定扰动区土体渗透系数沿径向线性变化;模式三:假定扰动区土体渗透系数沿径向抛物线变化,此模式是通过大量试验结果和实测结果拟合出来的近似变化模式。

图3 扰动区土体水平渗透系数三种变化模式Fig.3 Three variation modes of soil horizontal permeability coefficient in disturbed area

复合地基水平渗透系数kr(r)和复合地基竖向渗透系数kv(r)均是一个关于径向距离r的分段函数(见图3、图4),令kr(r)=khf1(r)、kr(r)=khf2(r),图中kh为复合地基未扰动区土体水平渗透系数。

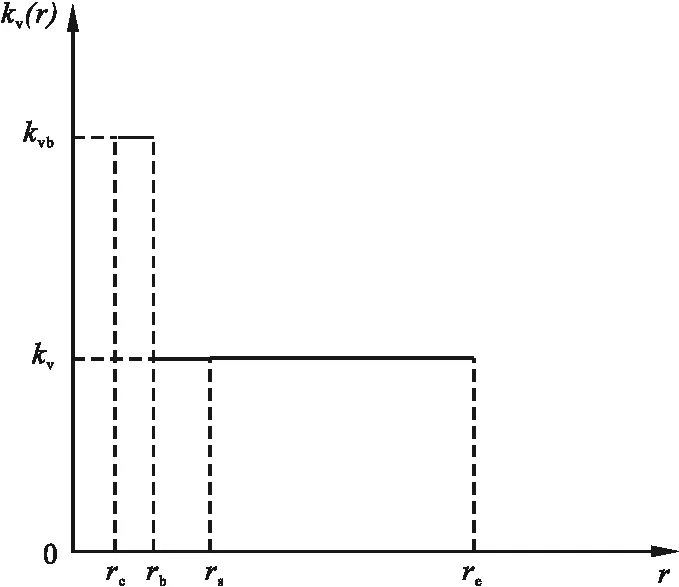
图4 复合地基竖向渗透系数变化模式Fig.4 Vertical permeability coefficient variation pattern of composite foundation

根据图2所示固结模型及布袋注浆桩桩体不透水,由等应变假定及平衡方程可得:

(1)

竖向应变关于时间t的偏导数为

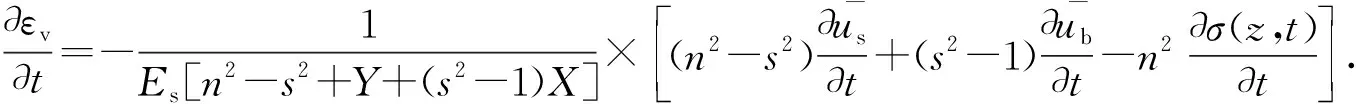
(2)

式中:n为桩径比,n=re/rc;s=rb/rc;X=Eb/Es;Y=Ec/Es。

地基土体内、布袋内以及布袋和土体内的平均孔压分别为

(3)

(4)

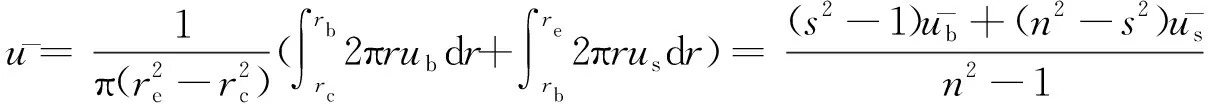
(5)

由式(2)和式(5)得:

(6)

由于布袋注浆桩复合地基的布袋-土界面为排水界面,而桩-布袋边界和单元体外边界不排水,所以得出径向边界条件为

(7)

根据谢康和等[18]在对称情况下考虑土体径向及竖向渗流时研究的固结方程作微分和积分,并结合式(7)对应的边界条件,得:

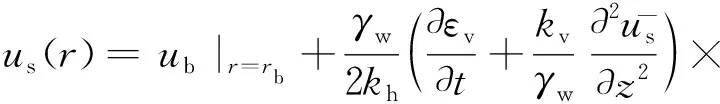
(8)

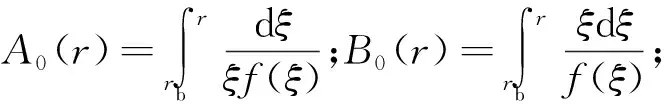
rb≤r≤re。

(9)

式中:kv为土体竖向渗透系数;γw为水的重力密度。

将式(8)代入式(3)、式(9)代入式(4),并将两式相减后联合式(5)、式(6)得:

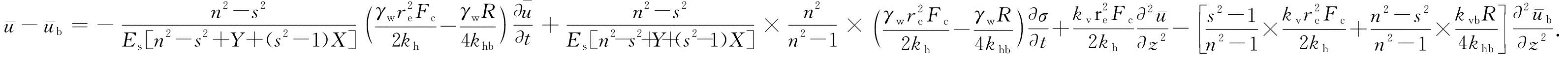
(10)

对式(8)和式(9)关于r微分,代入式(7)对应的边界条件,并结合式(5)、式(6)得:

(11)

其中,

将式(11)代入式(10)得:

(12)

其中,

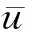
由于地基顶面排水,底面不排水,可得竖向边界条件为

(13)

2 固结控制方程求解

2.1 荷载瞬时加载条件下方程求解

由于在初始时刻土体和桩体没有发生变形,将等应变假定代入固结模型平衡方程,结合式(5)可得初始条件为

(14)

图5 瞬时加载情况下复合地基中附加应力随时间变化图Fig.5 Variation of additional stress in composite foundation with time under instantaneous loading

(15)

式中:

(16)

(17)

(18)

amλmcos(λmH)=0.

(19)

由于λm和am不能为零(否则解为零解),可知λm=M/H,M=(2m-1)π/2(m=1,2,…,),将条件带入式(16)解出βm,将式(15)、式(17)结合式(14)可得最终解:

(20)

(21)

复合地基的固结度可以定义为

(22)

把式(14)和式(20)代入式(22),得到瞬时加载情况下的布袋注浆桩复合地基固结度解析解:

(23)

2.2 荷载单级施加条件下方程求解

地基内附加应力是一个可以分离的变量,外部荷载单级施加且附加应力沿深度呈梯形分布(见图6),荷载非瞬时施加时,在地基内引起的附加应力为

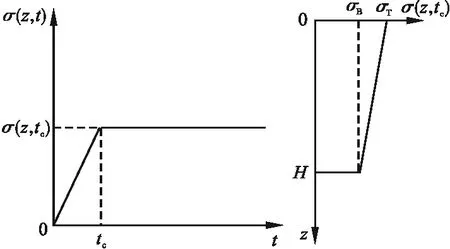
图6 荷载单级情况复合地基附加应力随时间和深度变化图Fig.6 Variation of additional stresses in composite foundations with time and depth under single-stage loads

(24)

式中:σT和σB分别为最大加载值时地基顶面和底面的附加应力值。

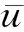
(25)

(26)

式中:

(27)

由初始时刻荷载为零结合式(25),可以得出满足初始条件Tm(0)=0的解,结合式(26)、式(27),代入式(25)得到地基内平均超静孔压:

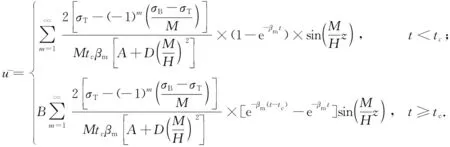
(28)

本节按应力定义的固结度来求解,布袋注浆桩复合地基固结度按应力可定义为任一时刻土体和布袋组合体内的有效应力和最终荷载即总应力之比,即:

(29)

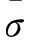
通过联合式(5)、静力平衡方程和等应变假定可得:

(30)

(31)

式中:Ez为布袋和土体组合体的等效压缩模量,G=Ec/Ez=(n2-1)Y/[n2-s2+(s2-1)X]。

(32)

3 解的验证

笔者根据布袋注浆桩的特性,采用新的求解方法及表达形式推导了布袋注浆桩复合地基在荷载瞬时施加和单级施加情况下的解析解,并且采用退化解与已有解的比较来对解析解的正确性进行验证。将常数A、C、D、F代入式(9)可解出βm的具体表达式为

(33)

式中:

令rb=rc,即不考虑布袋的影响作用,此时s=1,kvb=kv,将其代入到式(33)可得βm为

(34)

将s=1、kvb=kv代入式(32),可得到固结度解答退化为

(35)

式(35)与式(34)即为卢萌盟等[20]给出的单级荷载下附加应力沿深度非均匀分布的不透水桩复合地基的固结解答。

令σB=σT,式(35)退化为

(36)

式(34)和式(36)即为卢萌盟等给出的单级荷载下附加应力沿深度均匀分布的不透水桩复合地基的固结解答。

令tc→0,则式(36)中t≥tc对应的固结度解答退化为

(37)

式(34)和式(37)即为卢萌盟等给出的瞬时荷载下不透水桩复合地基的固结解答。也验证了笔者给出的瞬时荷载下布袋注浆桩复合地基固结解的正确性。

如果令n→∞(即rc→0),假设状体不存在,则式(34)的βm退化为

(38)

式(37)和式(38)即为Terzaghi一维固结解。显然,经过四重退化(rb=rc,σB=σT,tc→0和n→∞)即可退化为Terzaghi一维固结解。

4 复合地基固结特性分析

为分析影响布袋注浆桩复合地基固结的参数,对固结解答做进一步探讨,笔者采用控制变量法和取特殊值法,通过函数图形的比较,在六种不同参数的工况条件下对固结的影响进行分析,以期更为直观地对布袋注浆桩复合地基固结性状进行研究。文中取H=22 m,rc=0.2 m,布袋注浆桩复合地基桩间距为1.3 m,其余参数见表1。

4.1 布袋注浆桩复合地基固结度分析

对式(23)进行分析,绘出在瞬时加载时,扰动区土体水平渗透系数保持不变情况下(模式一),布袋注浆桩复合地基固结度与加载时间(U-lgt)的曲线(工况一)如图7所示,并与Terzaghi天然地基固结解、卢萌盟等[10]给出的散体材料桩复合地基和一般不透水桩复合地基固结解进行地基固结速率的比较。其中,取布袋桩渗透系数kvb=0.864 m/d,土体的渗透系数kv=8.64×10-5m/d,为了使曲线对比更加直观,取散体材料桩的渗透系数kc=0.864 m/d。

图7 四种地基形式的固结速率比较Fig.7 Comparison of consolidation rates of four foundation forms

由图7可知,在桩体压缩模量相同的前提下,四者的固结速率:散体材料桩复合地基的固结速率远大于不透水桩复合地基的固结速率,不透水桩复合地基的固结速率远大于天然地基,而布袋注浆桩由于布袋的排水作用,其复合地基固结速率远大于一般不透水桩复合地基的固结速率,模式二和模式三结果相似。但在工程应用中,布袋注浆桩并不以加速地基土固结为主要目的,而是为了提高地基承载力和减小地基沉降。

对式(32)进行分析,分别取σT/σB=0,σT/σB=0.4,σT/σB=1,σT/σB=2.5,σT/σB→∞进行布袋注浆桩复合地基固结度的计算。在荷载单级线性施加时,模式一情况下复合地基中附加应力分布形式对固结度的影响(工况二)如图8所示。从图中曲线可以看出,地基固结随着地基顶面和底面的附加应力比值的增大而加快。因为假定排水面设置在地基表面时,接近排水面处的附加应力越大,地基固结越快。

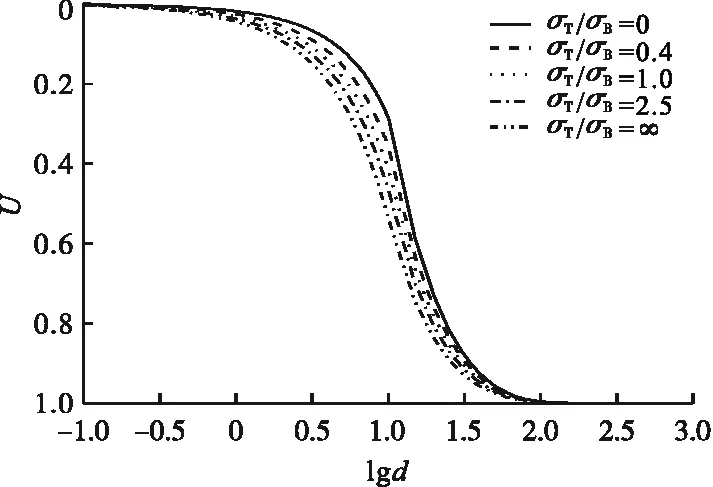
图8 附加应力分布形式对固结的影响Fig.8 Effect of additional stress distribution on consolidation

图9为扰动区土体水平渗透系数呈模式二变化时,加载历时对地基固结的影响(工况三)。从图中可知,加载历时越长,荷载施加得越慢,固结也就越慢。

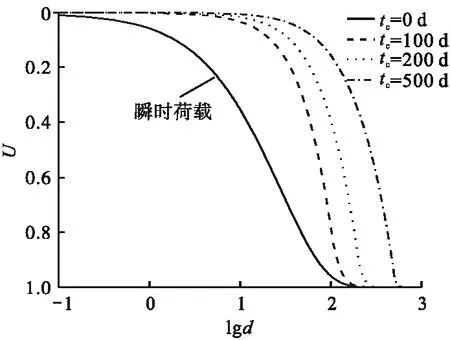
图9 加载历时对固结的影响Fig.9 Effect of loading elapsed on consolidation

图10为扰动区土体水平渗透系数呈模式二变化时,布袋注浆桩复合地基布袋渗透系数对地基固结的影响(工况四),分别取kvb=0.216 m/d,kvb=0.432 m/d,kvb=0.864 m/d,kvb=1.296 m/d,kvb=1.728 m/d进行计算。从图中可以看出,地基固结速率随着布袋渗透系数的增大而加快;当布袋渗透系数增大到一定程度,复合地基固结速率减缓,此时布袋渗透系数对地基的固结速率产生的影响很小,因此在设计布袋注浆桩复合地基时应合理选择布袋类型。

图10 布袋渗透系数对地基固结的影响Fig.10 Effect of cloth bag permeability coefficient on foundation consolidation

4.2 布袋注浆桩复合地基孔压分析

图11 某一时刻地基平均孔压沿深度分布形式Fig.11 The average pore pressure of the foundation at a certain time is distributed along the depth

图12为扰动区土体水平渗透系数呈模式二变化时,布袋注浆桩复合地基在单级线性加载情况下,加载历时对地基内平均孔压消散的影响(工况六),分别取tc=0,tc=5 d,tc=10 d,tc=20 d,tc=50 d,z/H=0.5进行复合地基平均孔压计算。从图中可以看出,当荷载非瞬时施加时,孔压首先由零逐渐增大,当荷载施加到最终荷载时,孔压也同时达到最大,随后开始减小直至孔压最终消散为零。另外随着加载历时增加,地基内的最大孔隙水压力值变小,因此为了减小地基内产生较大的孔隙水压力而导致的渗流破坏,可考虑采用减缓加载速率的方式来使荷载达到最终值。

图12 加载历时对地基内平均孔压消散的影响Fig.12 Effect of loading time on average pore pressure dissipation in the foundation

5 结 论

(1)在计算条件相同的情况下,散体材料桩复合地基的固结速率大于布袋注浆桩复合地基固结速率,布袋注浆桩复合地基固结速率大于不透水桩复合地基的固结速率,不透水桩复合地基的固结速率远大于天然地基。

(2)地基固结随着地基顶面和底面的附加应力比值的增大而加快,且接近地表的附加应力越大,固结越快。

(3)加载历时对地基固结的影响较大,加载历时越长,荷载施加得越慢,固结也越慢;外部荷载瞬时施加,此时地基固结最快,然而加载历时越久,地基内的最大孔隙水压力值越小。