轴压下三面受火中空钢管混凝土叠合长柱耐火性能研究

张 波,徐光朋,任庆新,3,秦笑笑

(1.沈阳建筑大学土木工程学院,辽宁 沈阳 110168;2.辽宁清创高科建筑工业化咨询有限公司,辽宁 沈阳 110179;3.佛山科学技术学院交通与土木建筑学院,广东 佛山 528225)

中空钢管混凝土叠合柱是一种由核心钢管和外围钢筋混凝土组成的新型组合构件,在高层建筑发展中具有十分重要的作用。李国强[1]和韩林海[2]对钢-混凝土组合结构的耐火性能进行研究。项凯[3]、L.Xu[4]和周侃[5]对均匀受火作用下钢管混凝土叠合柱的耐火性能进行了试验研究,指出试件在荷载和高温作用下的破坏模态呈现整体屈曲,且角部混凝土发生剥落现象,外围钢筋混凝土能够有效避免钢管发生局部屈曲,提高构件的耐火性能。侯舒兰[6]进行了考虑火灾降温作用下钢管混凝土叠合柱耐火性能理论研究,指出钢管混凝土叠合柱在降温阶段仍有可能发生破坏。H.Lu[7]和韩林海等[2]对均匀受火作用下中空夹层钢管混凝土柱的耐火性能进行了试验研究,指出试件均发生整体屈曲破坏,内置圆钢管时未发生局部屈曲现象。发生火灾时,由于结构柱所处位置不同,受火边界条件也不相同,有的结构柱处于非均匀受火状态[8],非均匀火灾作用下,构件会出现不均匀的挠曲变形和附加偏心距,降低了构件的耐火性能。叶友林[9]和张玉琢等[10]对三面受火方钢管约束钢筋混凝土柱耐火极限进行了研究,指出试件均发生整体屈曲破坏。王明涛[11]指出非均匀受火作用下钢管混凝土叠合柱外围混凝土开始降温时,核心钢管混凝土仍处于升温阶段,温度滞后明显。L.Xu等[12]对三面受火钢管混凝土叠合柱耐火极限进行了研究,提出了耐火极限实用计算公式。张玉琢等[13]对三面受火中空夹层钢管混凝土柱耐火极限进行理论研究,指出荷载比、长细比和界面尺寸是影响构件耐火极限的主要参数,并提出了耐火极限实用计算公式。其他学者也对构件非均匀受火进行理论研究,分析了影响构件耐火极限的主要参数,提出了剩余承载力实用计算公式[13-19]。

综上所述,笔者继续开展研究,利用ABAQUS有限元分析平台,选取合理的热工参数和材料本构模型对轴压下三面受火中空钢管混凝土叠合长柱的耐火性能进行分析,并提出了耐火极限简化计算公式。

1 有限元分析模型

1.1 模型建立

采用“热-力顺序耦合”的方法对轴压下三面受火中空钢管混凝土叠合长柱耐火性能进行分析。在温度场计算模型中,材料的热工参数按照T.T.Lie[20]的建议取值;假定中空钢管混凝土叠合长柱三面全高度受火,采用ISO-834标准升温曲线[21],初始温度设为20 ℃;钢管和混凝土采用DC3D8单元,纵筋和箍筋采用DC1D2单元;钢管与混凝土的接触面采用Tie约束,钢筋笼采用内嵌于混凝土中;受火面和背火面的热对流系数分别取25W/(m2·℃)和9W/(m2·℃),综合辐射系数取0.5[6]。

在力学性能计算模型中,钢管和混凝土采用C3D8R单元,纵筋和箍筋采用T3D2单元;钢管与混凝土相互作用在法向上定义为“硬接触”,在切向上采用摩擦系数为0.6的库伦摩擦[6];参考点RP1和RP2分别与中空钢管混凝土叠合长柱底表面和柱顶表面耦合;初始偏心距为1/1 000L。中空钢管混凝土叠合长柱的网格划分和受火方式如图1所示。

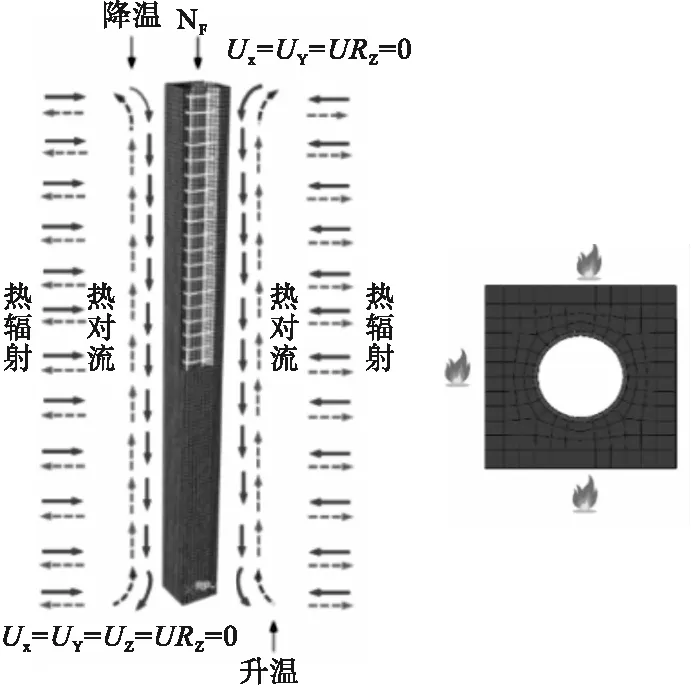
图1 网格划分与受火方式Fig.1 Meshing and fire mode

1.2 常温性能验证

为验证常温下中空钢管混凝土叠合长柱力学有限元分析模型的正确性,与文献[22-23]的空心钢管混凝土叠合柱轴压力学性能试验结果进行对比。图2为极限承载力计算值与试验结果对比曲线,Nuc/Nue的平均值为0.941,均方差为0.062,可见有限元模型可较好地预测轴压极限承载力。图3为轴向荷载-应变关系计算值与试验结果对比曲线,通过对比发现有限元模型可较好地预测空心钢管混凝土叠合柱轴向荷载-应变关系曲线的发展趋势。

图2 极限承载力计算值与试验结果对比Fig.2 Comparison of calculation value and test result of ultimate bearing capacity

1.3 耐火性能验证

为验证中空钢管混凝土叠合长柱有限元分析模型的正确性,与H.Lu[7]均匀受火方套圆中空夹层钢管混凝土柱和唐贵和[24]三面受火方钢筋混凝土柱温度场试验数据进行了对比;与H.Lu[7]均匀受火方套圆中空夹层钢管混凝土柱和周侃[5]均匀受火方套圆钢管混凝土叠合柱耐火极限试验数据进行对比。

图4为温度-时间关系计算值与试验结果对比曲线,试件SC1在d=65 mm时的温差稍大,这可能是因试件中空部分密封不好导致,且对于方套圆截面的计算值偏于安全。图5为轴向位移-时间关系计算与试验结果对比曲线,可见试件SC1耐火极限计算值偏安全,试件S0-2耐火极限吻合较好。故有限元模型可较好地预测三面受火作用下方套圆组合结构柱的耐火性能,且计算值偏于安全。

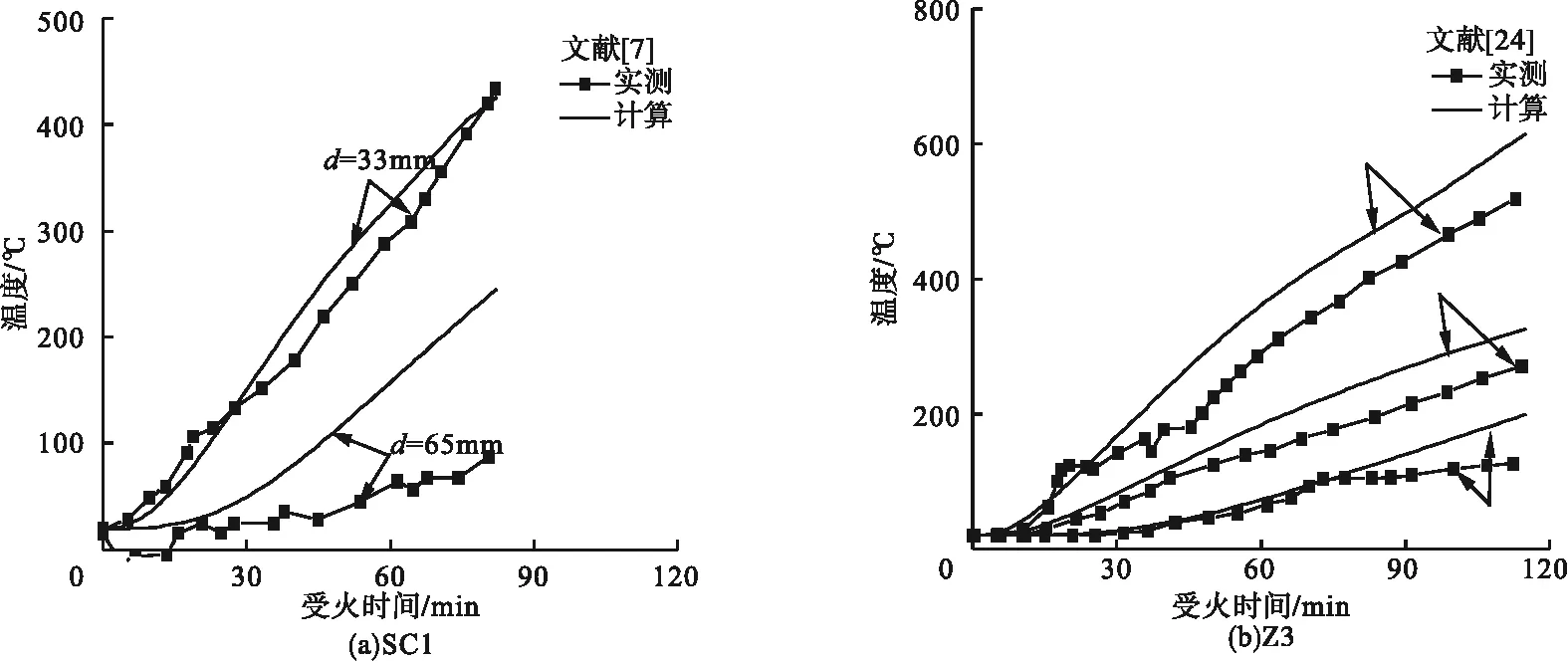
图4 温度-时间关系计算值与试验结果对比Fig.4 Comparison of the calculated value of temperature-time relationship with the experimental results

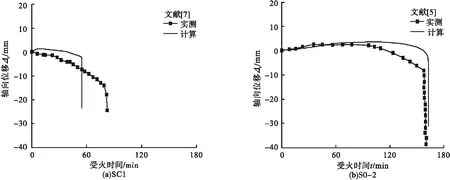
图5 轴向位移-时间关系计算与试验曲线对比Fig.5 Calculation of axial displacement-time relationship and comparison of test curves

2 受力机理分析

典型构件设计参数为B×D×t×L=300 mm×150 mm×7.5 mm×3 800 mm、火灾荷载比n=0.4、长细比λ=44、纵向钢筋为8Φ18(fy=335 MPa)、钢管牌号为Q345(fys=345 MPa)、混凝土型号为C50(fcu=50 MPa)、箍筋为Φ8@100(fy=300 MPa)。

2.1 温度-时间曲线

图6为中空钢管混凝土叠合长柱测点分布及温度-时间关系曲线。通过对测点1～5的温度对比发现,三面受火中空钢管混凝土叠合长柱截面温度从受火面到背火面有逐渐下降的趋势,钢管表面的温度要低于外围混凝土温度,说明外围钢筋混凝土对钢管起到了保护作用。

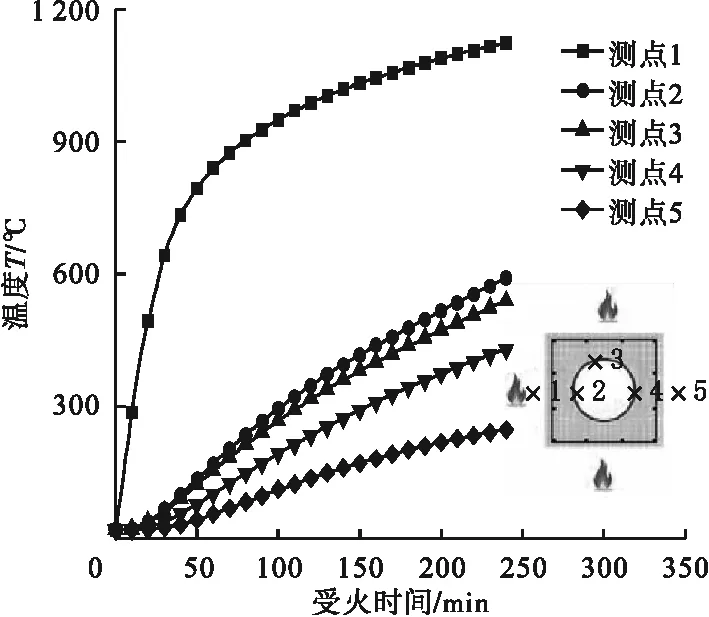
图6 温度-时间曲线Fig.6 Temperature-time curves

2.2 轴向位移-时间曲线

图7为三面受火中空钢管混凝土叠合长柱的轴向位移-时间关系曲线。三面受火中空钢管混凝土叠合柱变形主要分为3个阶段:①膨胀阶段,火灾作用初期,构件外部温度逐渐升高,随着温度升高,外部材料发生劣化,产生轴向膨胀变形;②加速变形阶段,火灾作用中后期,构件内部温度不断升高,材料劣化速率迅速增加,此时材料的压缩变形高于构件的轴向膨胀变形;③破坏阶段,火灾作用末期,构件材料劣化达到临界,构件所能承受的有效荷载小于轴向外荷载,此时构件的轴向压缩变形急速增快,轴向变形与受火时间关系曲线近似垂线。

图7 轴向位移-时间曲线Fig.7 Axial displacement time curves

2.3 破坏模态

图8为中空钢管混凝土叠合长柱的破坏模态。由图可见,轴压下三面受火中空钢管混凝土叠合长柱发生了压弯破坏,从整体破坏模态上看,构件具体表现为弯曲,柱中侧向挠度最大,破坏发生在柱中最大侧向挠度处,此区域内混凝土极易压溃、开裂。

图8 典型构件破坏模态Fig.8 Typical component failure modes

2.4 应变分布

图9为中空钢管混凝土叠合长柱在常温和升温时柱中截面混凝土纵向塑性应变分布。由图可见,常温加载结束时刻,因荷载比较小,未出现纵向塑性应变;在升温破坏时刻,因加载时考虑了初始偏心距以及温度场的不均匀分布产生的附加偏心距,柱中纵向塑性应变主要出现在高温受压区和低温受拉区,且呈偏心分布,此区域内的混凝土极易发生压溃、开裂。

图9 柱中截面混凝土纵向塑性应变分布图Fig.9 Longitudinal plastic strain distribution of concrete in column section

2.5 应力变化

图10为中空钢管混凝土叠合长柱在常温和升温时柱中截面混凝土纵向应力分布。由图可见,常温加载结束时刻,在考虑1/1 000L初始偏心距下,混凝土纵向应力呈条带分布;升温破坏时刻,因受火面材料劣化程度较大,混凝土纵向压应力主要集中在受压区靠近钢管温度相对较低处,混凝土纵向拉应力主要集中在靠近背火面温度相对较低处。

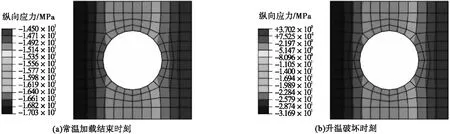
图10 柱中截面混凝土纵向应力分布图Fig.10 Longitudinal stress distribution of concrete in column section

2.6 内力变化

图11为轴压下三面受火中空钢管混凝土叠合长柱各组成部分轴力-时间关系曲线。在常温加载结束时刻(t=0),混凝土、纵筋和钢管分担的内力分别占外荷载的66.11%,10.71%和23.18%。在火灾作用初期,外围混凝土和纵筋的温度远高于截面内部钢管,高温下混凝土和纵筋热膨胀变形更大,其强度在火灾作用初期损失较小,分担的内力增大。在火灾作用中后期,混凝土和纵筋的温度不断升高,高温导致其强度损失严重,而钢管受混凝土热惰性保护,其温度较低,混凝土和纵筋卸载下来的内力由钢管分担,钢管分担的内力增大。在升温破坏时刻(t=83.87 min),混凝土、纵筋和钢管分担的内力分别占外荷载的50.98%,13.49%和35.53%。

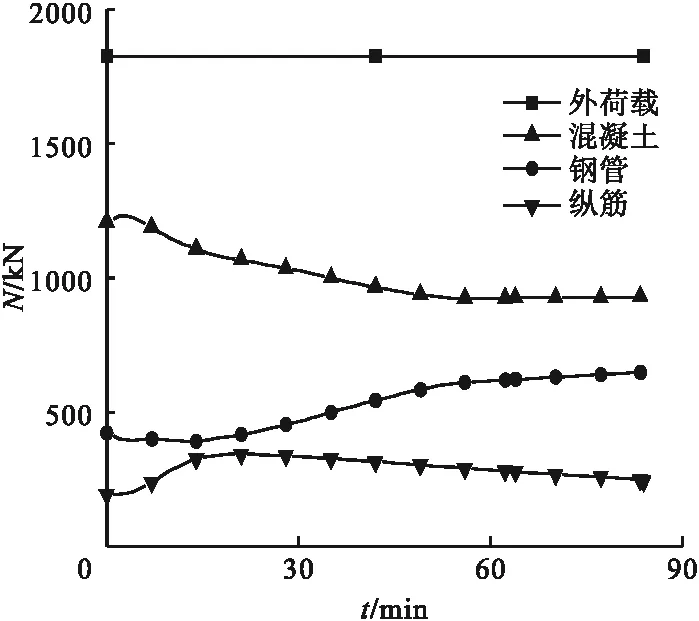
图11 各组成部分的轴力-时间关系Fig.11 Axial force-time relationship of each component

2.7 两种柱的耐火性能比较

中空钢管混凝土叠合柱可看成由钢管和外围钢筋混凝土叠合而成的一种组合构件。为了解此类组合构件在三面受火作用下是否比中空钢筋混凝土柱的力学性能更优秀,根据典型算例的设计参数,建立了无钢管的中空钢筋混凝土柱的耐火性能有限元计算模型。图12为中空钢筋混凝土柱与中空钢管混凝土叠合柱在三面受火作用下的轴向位移-时间关系曲线对比。从图中可以看到,中空钢管混凝土叠合柱的耐火极限明显高于中空钢筋混凝土柱,这是因为位于截面核心的钢管受外围混凝土的包裹,钢管在高温下的劣化程度远远小于外围混凝土,使混凝土卸载下来的荷载逐渐转移到截面核心位置的钢管上,因而,中空钢管混凝土叠合柱具有更好的耐火性能。

图12 两种柱的轴向位移-时间曲线对比Fig.12 Comparison of axial displacement-time curves of two kinds of columns

3 参数分析

空心率(χ)、截面边长(B)、长细比(λ)、荷载比(n)等参数对轴压下三面受火中空钢管混凝土叠合长柱耐火极限的影响如图13所示。

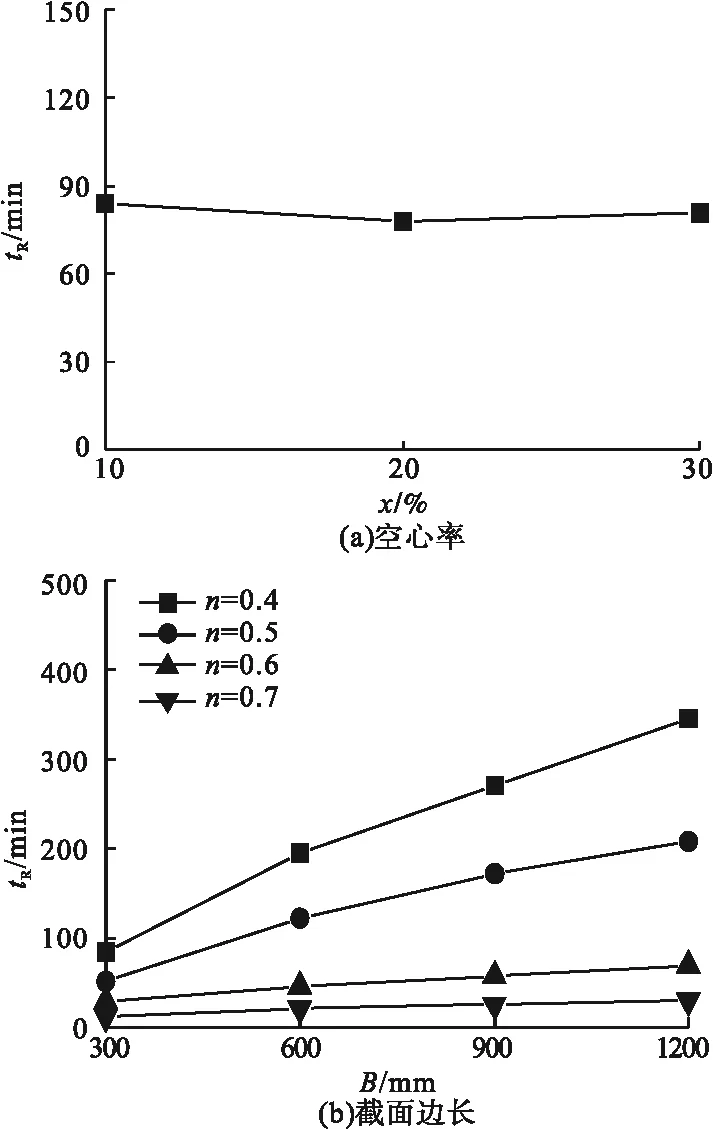
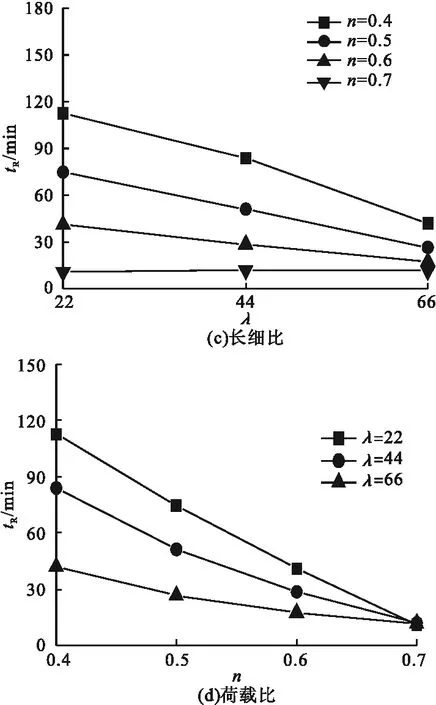
图13 参数对耐火极限的影响Fig.13 Influence of parameters on fire resistance

3.1 空心率

从图13中看出,空心率对耐火极限的影响较弱,空心率为20%时,中空钢管混凝土叠合长柱的耐火极限最低。故从实际应用和安全的角度出发,空心率设定为20%。

3.2 截面边长

耐火极限与截面边长成正比,随着截面边长的增加,基于混凝土的热惰性,导致温度向截面内传递变慢,延缓了截面内部升温,当截面边长由300 mm增加至600 mm、900 mm和1 200 mm时,耐火极限增加了131.83%、221.81%和312.02%。

3.3 长细比

耐火极限与长细比成反比。当长细比由22增加至44和66时,耐火极限分别降低了25.46%和62.77%。随长细比增加,构件破坏形式由材料劣化引起的轴压破坏变为由刚度迅速下降引起的压弯破坏。

3.4 荷载比

耐火极限与荷载比成反比。随着荷载比的增加,构件内混凝土和钢材允许劣化程度越小,当荷载比由0.4增加至0.5、0.6和0.7时,耐火极限分别降低了39.03%、65.71%和85.54%。故荷载比越大,构件的耐火极限越小。

4 实用计算方法

在参数分析的基础上,对此类构件的耐火极限进行基于非线性回归方法的曲线拟合。试件设计基本参数同典型构件设计参数,参数范围取n为0.4～0.7、λ为22～66、B为300～1 200 mm。对轴压下三面受火中空钢管混凝土叠合长柱的耐火极限简化计算,得到:

tR=(-0.031B2+85.118B-14 423.954)×λ-0.786(1-n)3.936+6.422.

(1)

图14为笔者提出的耐火极限简化计算公式计算值与有限元模型结果对比,两者比值的平均值为0.940 3,均方差为0.143 7,可见两者吻合程度较好。

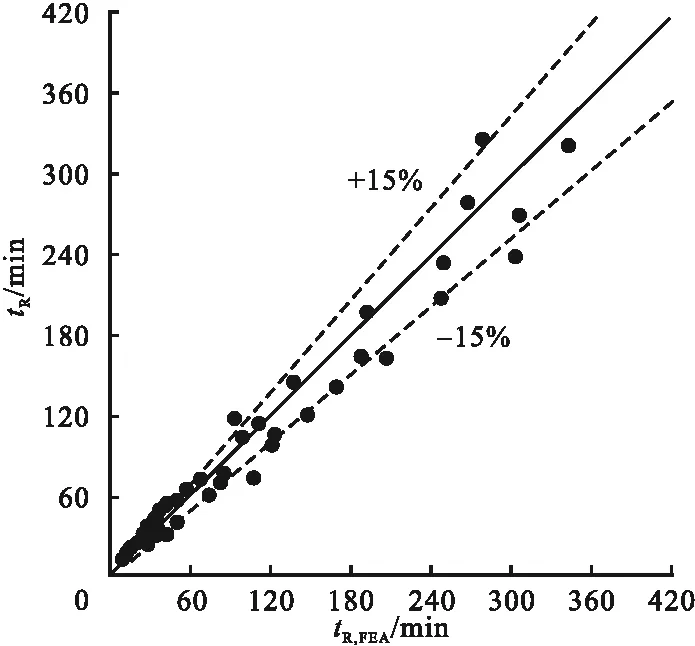
图14 耐火极限计算值与有限元结果对比Fig.14 Comparison of calculated fire resistance limits and finite element results

5 结 论

(1)因材料高温劣化和温度不均匀分布,轴压下三面受火中空钢管混凝土叠合长柱随着受火时间增加,轴向荷载逐渐向内部钢管转移,截面内力发生重分布,在升温破坏时刻构件柱均发生压弯破坏,与长细比无关。

(2)在轴向荷载和三面受火共同作用下,中空钢管混凝土叠合柱比中空钢筋混凝土柱具有更好的耐火性能。

(3)提出的耐火极限简化公式计算值与有限元计算结果吻合较好。