全栓接蜂窝梁柱端板连接空间节点梁铰机制有限元分析
贾连光,李秋镕,郑圆维,王春刚
(1.沈阳建筑大学土木工程学院,辽宁 沈阳 110168;2.中国建筑东北设计研究院有限公司,辽宁 沈阳 110006)
传统钢框架结构施工中,梁柱节点需要在现场进行大量焊接,受天气及人工等因素影响,焊缝质量难以保证,存在安全隐患。全栓接蜂窝梁柱端板连接节点,可以有效保证连接工作的可靠性,缩短施工周期,利于节能减排,所采用的蜂窝梁可以方便管道穿越其中,并能减轻结构自重,提高建筑美感。在以往的研究中,强轴向蜂窝梁H型柱连接中蜂窝梁上塑性铰的形成需要合适的开孔距离、开孔率、孔型及足够的连接刚度[1-11]。对于弱轴向的研究还很缺乏,K.Sang-dae等[12]对弱轴向3种端板连接形式的梁柱节点进行了试验研究,并对比弱轴向刚接梁柱节点,发现采用端板连接会使节点承载能力大幅下降;王湛等[13]在对全栓接弱轴节点进行试验研究中发现塑性铰易发生在端板上;徐莹璐等[14]通过设置肋板对弱轴节点进行加强,实现了塑性铰外移。
上述研究表明,强轴向蜂窝梁柱端板连接节点梁铰机制的形成需要足够的连接刚度,同时蜂窝梁需要提供足够的节点转动贡献率。由于弱轴向蜂窝梁柱端板连接的梁铰机制不明确,梁柱端板连接节点中各组件间独立变形和相互影响的特性使空间型节点、中节点及边节点的力学性能相差较大[13],因此,笔者提出一种全栓接蜂窝梁柱端板连接空间型节点,考虑强弱轴连接变形的相互作用,明确蜂窝梁柱端板连接节点强弱轴向的受力机理,研究连接刚度和连接转动贡献率对蜂窝梁柱节点力学性能、破坏形式、梁铰机制的形成及发展规律的影响,为工程设计提供参考。
1 有限元模型建立及验证
1.1 强轴向节点有限元模型验证
蜂窝梁柱端板连接有限元模型的关键是螺栓预应力的施加和孔角的应力集中,因此,笔者依照文献[15]中强轴向蜂窝梁柱端板连接节点试验建模,并进行验证,在此基础上建立空间型节点模型。试件中H型柱的截面为400 mm×300 mm×12 mm×16 mm,蜂窝梁的截面为400 mm×200 mm×8 mm×12 mm;梁腹板开孔率为60%(孔高/梁高),孔形为正六边形;螺栓采用10.9级M22高强摩擦型螺栓,试件所用钢材牌号为Q355;柱上下铰接,柱顶施加1 000 kN集中荷载,梁端通过作动器施加位移。
依照试验尺寸建立有限元模型。钢材的本构关系选用双折线模型,弹性模量为2.05×105MPa,泊松比为0.3,屈服强度为346 MPa,抗拉强度为584 MPa;高强螺栓的本构关系选用双折线模型,弹性模量为2.05×105MPa,泊松比为0.3,屈服强度为910 MPa,抗拉强度为1 020 MPa。模型的单元类型为C3D8I,螺栓预应力通过螺栓施加荷载,螺栓与梁柱试件的接触面、端板与柱面的接触面均定义为“罚摩擦”,摩擦系数为0.33;通过限制耦合点的位移与转角实现边界条件的布置。有限元与试验得到的荷载-位移曲线对比见图1(a),破坏形式对比见图1(b),由图可以看出,极限承载力相差0.6%,极限承载力所对应的位移值相差1.3%,说明有限元模型的计算精度较好。

图1 有限元模型验证Fig.1 The validation of finite element model
1.2 蜂窝梁柱端板连接空间型节点
笔者提出一种蜂窝梁柱端板连接空间型节点(见图2),由H型钢柱、强轴向端板、弱轴向环端板、蜂窝梁及高强螺栓组成。强轴向蜂窝梁与端板通过焊接形成一体,柱翼缘与环端板通过高强螺栓相连(见图2(b)),弱轴向蜂窝梁、补强板及环端板通过焊接形成一体,弱轴向环端板与柱腹板通过高强螺栓相连(见图2(c))。

图2 蜂窝梁柱端板连接空间节点Fig.2 Three dimensional beam-to-column joints with end-plate connection
1.3 蜂窝梁柱空间节点有限元模型建立
在上述建模技术的基础上建立蜂窝梁柱端板连接空间节点有限元模型(见图3(a)),梁柱截面、强轴向端板截面及各试件尺寸与试验试件一致,弱轴向环端板尺寸见图3(b)。端板的厚度将主要决定连接刚度,开孔距离与开孔率对蜂窝梁的节点转动贡献率影响较大,因此,考虑上述因素,采用正交试验方法共设计36个蜂窝梁柱端板空间节点模型,节点模型的相关尺寸见表1。试件编号命名为DCECxyz,x表示端板厚度,分别取8 mm、12 mm、16 mm;y表示开孔距离与梁高的百分比,即开孔距离分别为200 mm、300 mm和400 mm,分别定义为50、75、100;z表示开孔率,即开孔高度与梁高的百分比,分别定义为55、60、65、70。如编号DCEC805055的试件表示端板厚度为8 mm、开孔距离与梁高比为0.50、开孔高度与梁高比为55%。建模方法及边界条件与1.1节中一致,同轴向两侧梁端的加载方式为等值反向加载,采用位移控制加载,强弱轴向梁端施加竖向位移绝对值之比为1,柱顶施加1 000 kN集中荷载,模拟空间节点在遭受水平荷载作用时的实际工况。

表1 模型几何尺寸Table 1 Dimensions of the model mm

图3 蜂窝梁柱端板连接空间节点有限元模型Fig.3 Finite element model of three dimensional beam-to-column joints with end-plate connection
2 参数化分析
2.1 破坏形式
弱轴向环端板抗弯刚度较小时,即连接刚度较小时,环端板承担大部分弯矩,以力偶的形式通过补强板和螺栓传递给柱翼缘,节点域上下柱翼缘发生剪切错动,在轴向荷载作用下,柱发生严重弯曲,腹翼缘屈服,蜂窝梁几乎没有变形,将此破坏模式定义为RSF1。环端板抗弯刚度较大时,即连接刚度较大时,柱节点域剪切错动相对较小,柱的弯曲程度相对严重,同时蜂窝梁对节点转动有一定贡献率(即蜂窝梁自发变形带动节点转动),此时柱翼缘、蜂窝梁翼缘发生屈服,将此破坏模式定义为RSF2。当环端板抗弯刚度很大时,即连接刚度很大时,节点域整体变形较小,蜂窝梁对节点转动贡献率较大,节点的破坏形式为梁端开孔截面塑性铰破坏,将此破坏模式定义为RSF3,各破坏模式见图4。端板厚度大于0.75tcw(柱翼缘厚度)时,对破坏模式的影响较小。此外,强轴向变形对弱轴的破坏形式影响较小。
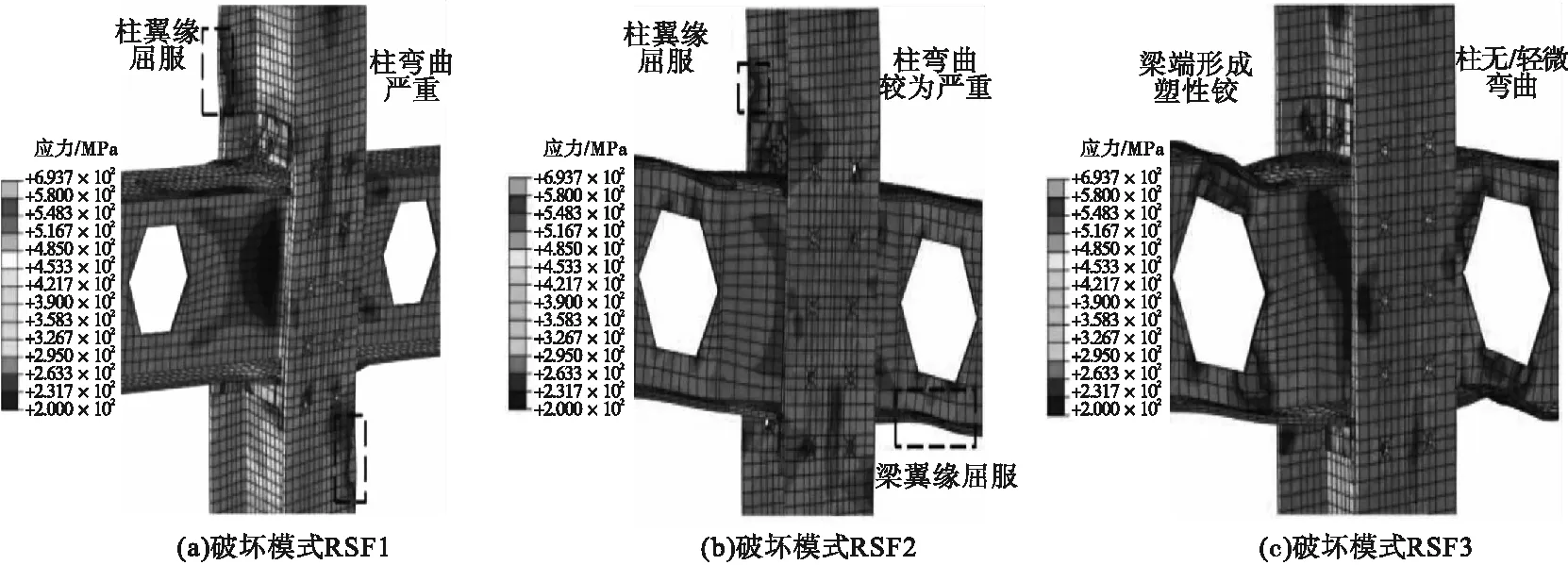
图4 弱轴向破坏形式Fig.4 The weak axial failure mode
强轴向端板连接刚度较小时,端板发生端板屈服破坏,将此破坏模式定义为QSF1(见图5(a))。端板连接刚度较大时,端板与柱翼缘可以协同变形,蜂窝梁在协同变形期间可以对节点转动作出贡献,节点发生多组件塑性破坏(见图5(b)),在试验研究中当节点发生此类型破坏时,在连接焊缝保证稳定工作的情况下,节点具有良好的变形与承载能力[15],将此破坏模式定义为QSF2。端板连接刚度足够时,柱翼缘几乎不发生强轴向的弯曲变形,此时,弱轴向的柱弯曲变形对破坏形式的影响较小,蜂窝梁上发生梁端开孔截面塑性铰破坏(见图5(c)),将此破坏模式定义为QSF3。端板厚度、开孔距离及开孔位置对强轴向的破坏模式影响很大,当端板厚度大于tcw,当开孔率大于 60%时,强轴向蜂窝梁均能形成梁铰破坏机制,此时弱轴柱变形对其破坏形式的影响很小,反之弱轴向的柱变形将对强轴向的破坏形式具有重要影响。
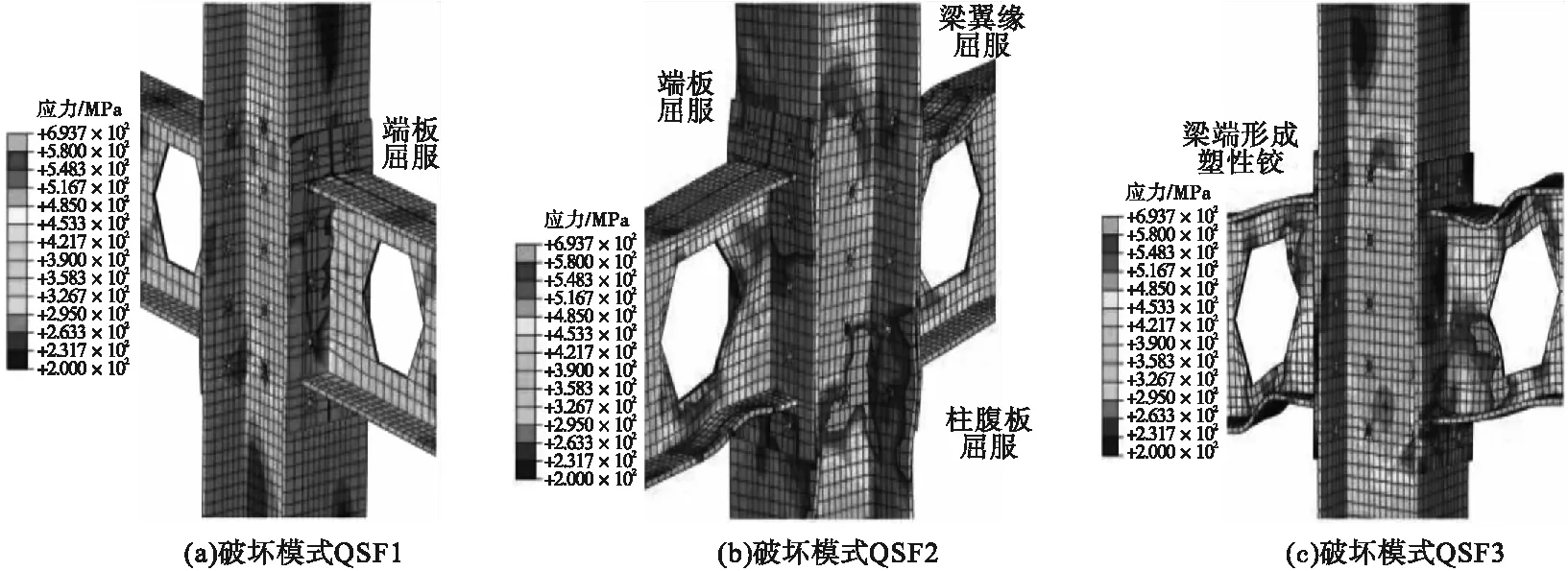
图5 强轴向破坏形式Fig.5 The strong axial failure mode
2.2 承载能力
图6为蜂窝梁柱端板连接空间节点梁端加载点荷载-位移曲线。文献[3]提出ABAQUS不能很好地模拟端板出现撕裂时的力学性能,因此DCEC8系列很难正确模拟极限荷载。对比图6(b)、(c)可以发现,端板厚度对强轴向节点的极限承载能力及延性有很大的影响,但并不是端板厚度越大,节点的承载性能越好,节点的承载性能与节点的破坏形式有密切联系。强轴向破坏模式QSF2的极限承载能力与延性在总体上要大于其他两种破坏模式,破坏模式QSF1与QSF3的极限承载能力难以比较,但破坏模式QSF3的延性相对较好。在相同破坏模式下开孔率与极限承载能力、延性呈反比关系;开孔位置也是如此,只是开孔位置的影响相对较小,当开孔率大于65%时,节点强轴向的极限承载能力下降明显,开孔率为70%的试件的极限承载力较开孔率为65%的试件最大下降23.1%;开孔位置小于0.75倍的梁高时,极限承载力同样下降明显。因此在工程设计时,强轴向蜂窝梁的开孔率(正六边形孔)不宜大于65%,开孔位置不宜小于0.75倍梁高,端板厚度宜大于0.75倍柱翼缘厚度。
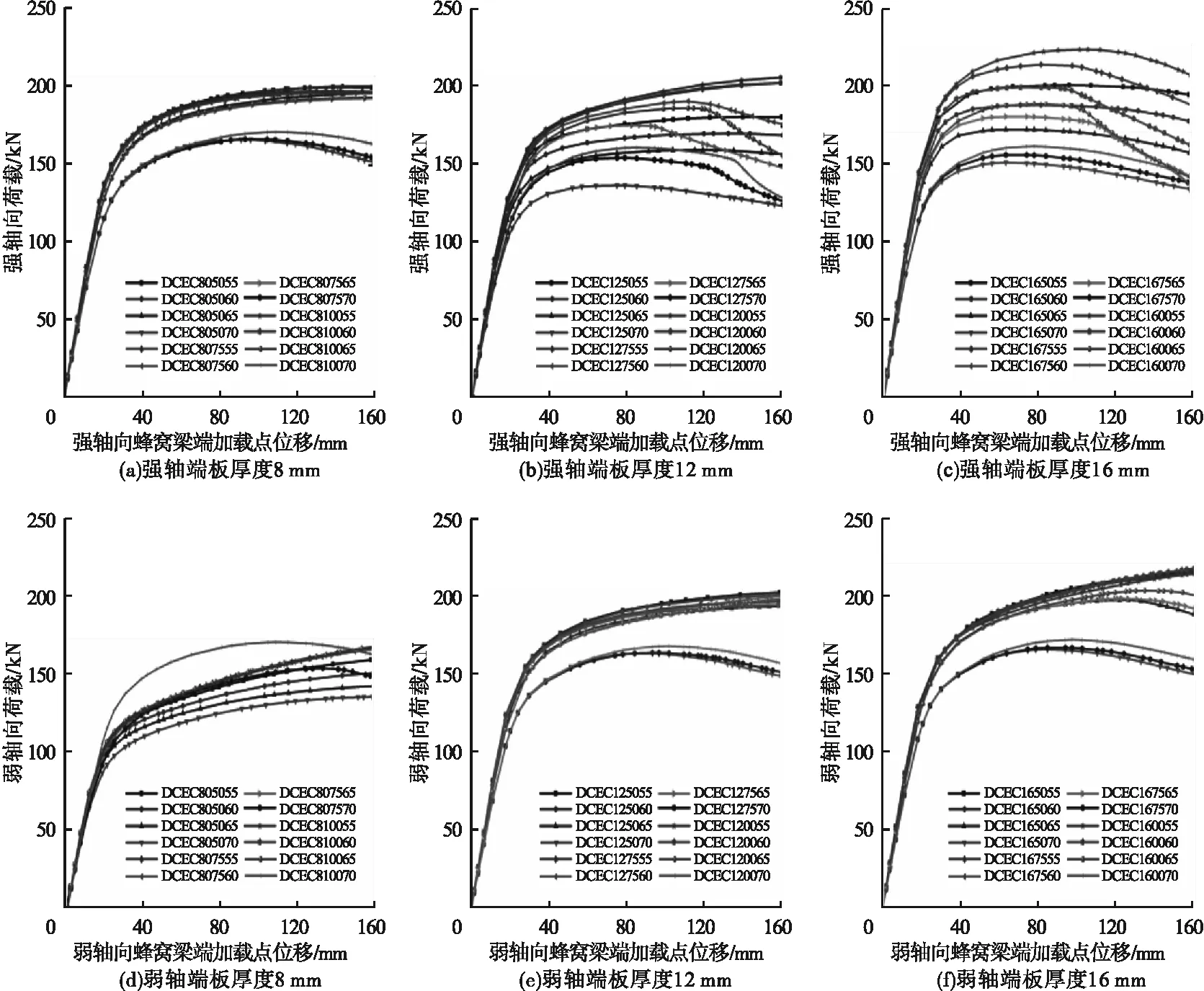
图6 荷载-位移曲线Fig.6 The loading-displacement curves
节点弱轴向的极限承载能力与环端板厚度呈非线性正比关系(见图6(d)~(f)),当环端板厚度大于0.75倍柱翼缘厚度时,随厚度增加的增长有限,此时破坏形式和开孔位置对极限承载能力的影响比较小,开孔率对极限承载能力的影响比较大,开孔率大于65%时,极限承载能力出现大幅下降。
3 弱轴向蜂窝梁节点转动贡献率计算
弱轴向对连接转动有贡献的组件如图7所示。柱腹板受弯、端板受弯、柱翼缘受剪对节点域转动θcon贡献率较大。DCEC16yz系列中螺栓没有发生明显变形(见图7(e)),DCEC8yz系列与柱翼缘相连的端板在弱轴向的变形不明显(见图7(d)),节点转动中心位于中间排螺栓孔中心(见图7(c)),由于连接板件厚度相对较大,因此,螺栓撬力的影响不被考虑在内。
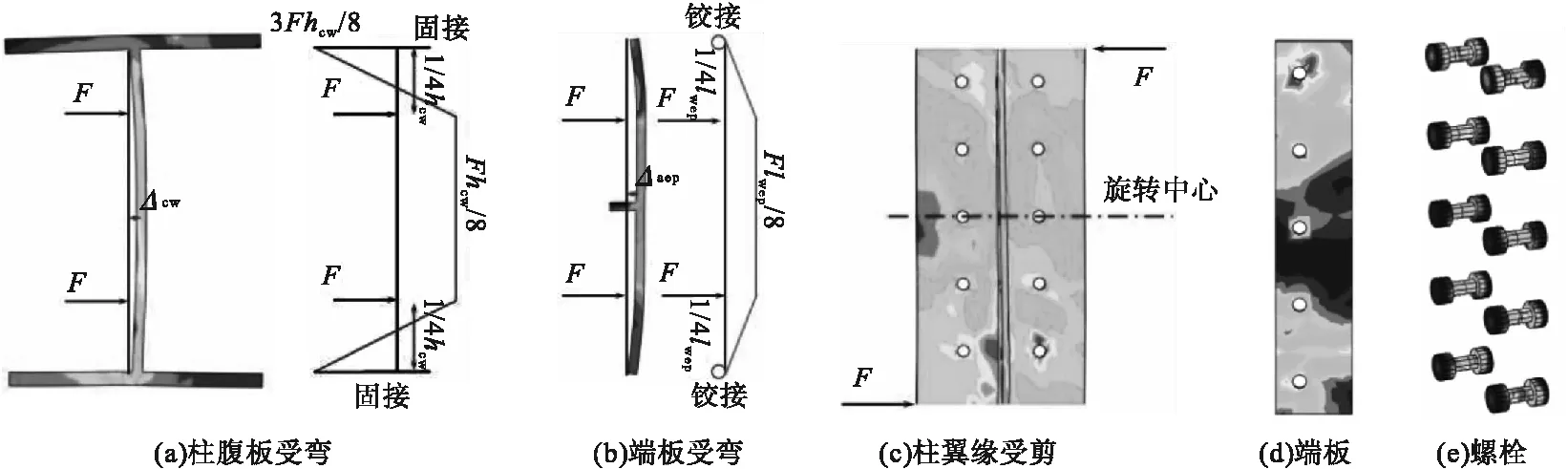
图7 组件对节点转动贡献Fig.7 The component contribution for joint rotation
将柱腹板与相连端板视作T型件的一部分,采用等效T型件法及图乘法计算抗弯刚度,柱腹板可视作两端固接梁受一对集中荷载作用(见图7(a)),根据计算得到:
(1)
式中:hcw为柱腹板高度;Icw为柱腹板截面惯性矩。
与柱腹板连接端板可视作两端铰接梁受一对集中荷载作用(见图7(b)),根据计算得到:
(2)
式中:lwep为端板宽度;Iwep为端板截面惯性矩。
弱轴向的柱腹板缺少平面外约束,在整个加载过程中,柱腹板与端板间紧密相连,因此,能与端板形成良好的协同变形。假定端板与柱腹板变形一致,得到柱腹板与端板连接部分的转动θcwep:
(3)
式中:hcb为蜂窝梁高。
柱翼缘受剪引起的节点域转动θcf,v计算式为
(4)
式中:β为与连接受剪边数有关参数,取2;Zcf为柱腹板受剪区域高度;Acf为柱两侧翼缘的有效抗剪面积。
节点域转动θcon可视作θcf,v与θcwep之和:
θcon=θcf,v+θcwep.
(5)
弱轴向蜂窝梁节点转动贡献率χ由下式计算得到:
(6)
式中:θcb为蜂窝梁的转动变形,即蜂窝梁端的挠度wcb与梁受力段长度的比值,wcb计算公式见文献[15]。
将DCEC16yz系列代入式(6)计算得到的计算值与有限元值(第一个峰值点)的对比,如表2所示。可以看出误差均在10%以内,误差平均值为4.19%,标准差为2.9%,具有较好的可靠性。
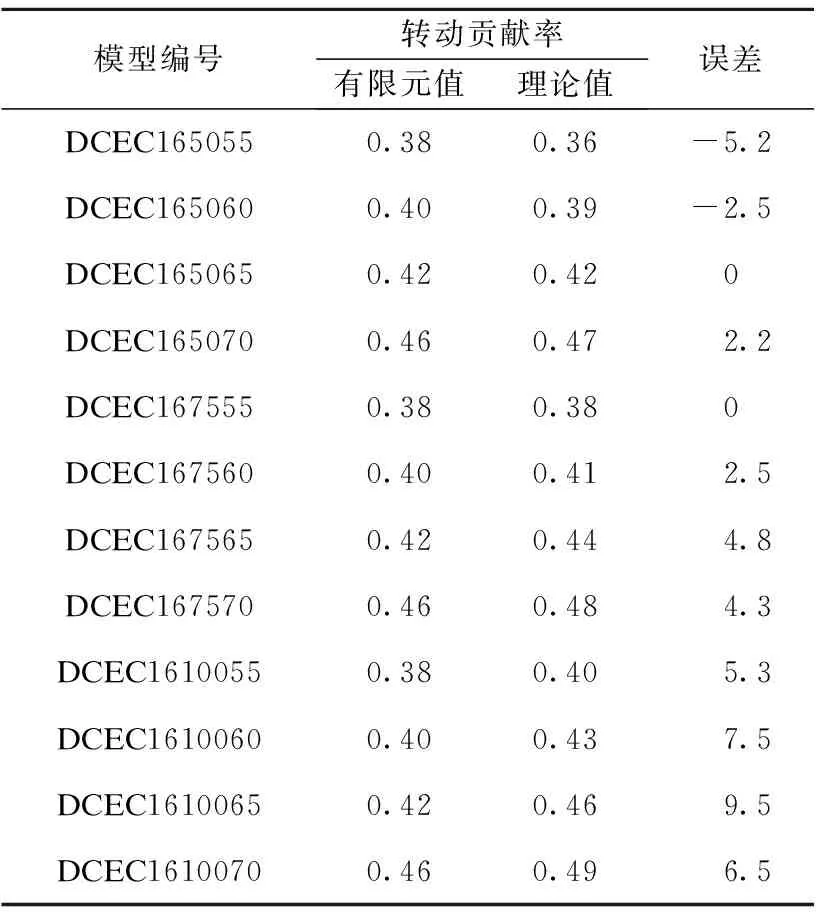
表2 理论与有限元值误差Table 2 Difference between TM and FEM %
4 结 论
(1)蜂窝梁柱端板连接空间节点强弱轴向最终均可形成梁铰破坏机制,端板连接刚度及蜂窝梁节点转动贡献率对节点的破坏形式及承载能力有重要影响,弱轴向弯曲会影响强轴向连接的力学性能,强轴向柱翼缘弯曲对弱轴向连接的力学性能及破坏形式影响较小。
(2)强轴向端板厚度应大于柱翼缘厚度,蜂窝梁开孔率建议取为60%~65%,开孔距离建议取0.75~1.0倍梁高,弱轴向蜂窝梁开孔率建议取65%~70%;受外伸补强板影响,开孔距离建议取值范围与强轴向一致,端板厚度宜大于0.75倍柱翼缘厚度;
(3)蜂窝梁节点转动贡献率可作为节点强弱轴向破坏模式的识别指标,基于等效T型件法及组件法提出了弱轴向蜂窝梁节点转动贡献率的计算方法,经验证具有良好的精度。

