基于MFBM模型对亚式期权模拟定价的研究

陈敦勇,孙玉东

(1.贵州民族大学 数据科学与信息工程学院,贵阳 550025;2.贵州民族大学 商学院,贵阳 550025)

近年来,随着金融市场的不断发展,各种理财产品层出不穷。期权是新型金融衍生品,可作为套期保值的工具。这是因为在当今的金融市场环境中,随着经济的快速发展,金融市场瞬息万变,投资风险也越来越大,而期权能有效利用对自身有利的风险来获取利润,从而起到套期保值、风险管理的作用,因此备受投资者的关注。市场大量出现的新型期权,更是满足了投资者的避险需要。如何对这些新型期权进行合理的定价一直是大家关注的问题。

期权的准确定价取决于标的资产价格的准确定价,所以,正确描述标的资产价格运动规律非常必要。多资产亚式看涨期权,其收益不是由1种资产所决定,而是依赖于多种资产共同决定。此外,亚式期权是路径依赖期权,在对冲和降低风险方面表现得更稳健,是经常被用于衡量市场风险的首选对象。自20世纪70年代布莱克-斯科尔斯(Black-Scholes,B-S)期权定价公式诞生以来,对期权定价的研究成果大量增加,但多数是在几何布朗运动的模式下进行的。另外,分数布朗运动的增量并不是独立的,当Hurst指数(H)>0.5时,分数布朗运动具有正相关增量,这意味着历史波动可能具有持久的影响。因此,分数布朗运动更适合描述金融资产的波动,并且表现出自相似和长距离依赖的特性,能够捕捉到典型的金融收益行为,比几何布朗运动更适合描述金融资产的波动。

综上所述,以往大多数研究都关注单资产期权定价(即只有1个标的资产价格),对于多资产期权研究的文献不多,基于此,提出基于MFBM模型两资产亚式期权的定价问题。其中,构造了2个标的资产所满足的偏微分方程,该方程包含2个变量(对应标的资产S1、S2),推导了MFBM模式下两资产亚式期权的定价公式,最后对无风险利率、H、资产价格的相关系数等重要参数对亚式彩虹期权价格的影响进行敏感性分析,以讨论所构造的方法对多资产期权定价的合理性和有效性。

1 分数布朗运动

定义1随机过程{Bt,t≥0}是布朗运动[13],也称为维纳过程(Wiener process),若σ=1即Bt-Bs～N(0,t-s),则{Bt,t≥0}为标准的布朗运动。除此以外还有带漂移项的布朗运动:如果随机过程{Xt,t≥0}满足dXt=μdt+σdBt,则{Xt,t≥0}为带漂移项的布朗运动,μ和σ(μ、σ可能都是时间t的函数,不一定为常数)分别为漂移系数和扩散系数。若随机过程{Xt,t≥0}满足Xt=exp(Bt),那么{Xt,t≥0}称为几何布朗运动,其满足对于∀u>t,给定Xt后,对数形式的布朗运动是正态的lnXt～N(lnXt+(α-0.5σ2)(u-t),s2(u-t))。

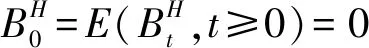
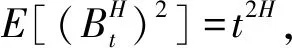
2 两资产亚式期权在MFBM模式下的定价模型

2.1 模型的建立

接着,考虑关于2项标的资产的最大值看涨亚式期权,其标的资产分别用S1、S2表示,则期权价格可由下式表达:

ψ(I1(T),I2(T),T)=max(max(P1(I1(T)),P2(I2(T)))-K,0),

(1)

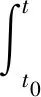
(2)

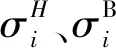
(3)

其中,E[·]代表期望。在连续时间假设下,标的资产S1和S2满足以下微分方程:

(4)

假设V(S1,S2,I1,I2,t)表示2项资产S1、S2在t时刻各自的价格,单位为元。由式(2)可知,期权价格V(S1,S2,I1,I2,t)满足以下定理:

定理1两资产亚式看涨期权价格满足偏微分方程

(5)

并有终边条件V(S1,S2,I1,I2,T)=max(max(P1(I1(T)),P2(I2(T)))-K,0)+。其中,H∈(0,1),σH为带参数H的波动率;ρ为相关系数;∂V/∂t表示期权价格V对时间t的偏微分;当年利率为2%时,无风险利率r=0.02。

证明首先对上述偏微分方程用泰勒展式展开,可得

(6)

其中,dS1、dS2可由式(2)给出,并且由上述几何平均Ii(t)可知

朱熹写过这样一句诗，“问渠那得清如许？为有源头活水来”。所谓“活水”，则是源源不断的清水。这句诗用来阐述读书的好处是再合适不过了，“活水”对于一汪清泉来说尚且是这个道理，那么它对于人创作的作用就可想而知了。读书数目和种类越多的人，把书读得越透越清楚的人，他们在创作的时候自然是“文思泉涌”，各种新颖的、秉具个人风格和特色的作品就能轻易地呼之欲出。

(7)

从文献[6,14]可知

(8)

(9)

把式(7)～(9)代入式(6),且令dt→0,那么式(6)可改写为式(10),如下:

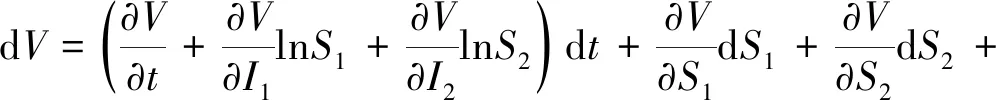
(10)

假设1个投资组合为F(t)且满足F(t)=V-L1S1-L2S2,其中,Li(i=1,2)表示在时间区间(t,t+dt)上产生的标准无套利,对于任意投资组合都满足dF(t)=rF(t)dt,有d(V-L1S1-L2S2)=r(V-L1S1-L2S2)dt,即

dV-d(L1S1+L2S2)+r(L1S1+L2S2)dt=rV。

(11)

再将式(10)代入式(11)可得式(12),如下:

(12)

且其中的投资组合F(t)是无套利机会的,选择Li=∂V/∂Si(i=1,2),再把该投资组合Li代入式(12),简化之后得到式(5),证毕。

由定理1可知,两资产亚式最大值看涨期权的收益函数V(I1,I2,S1,S2,T)满足

(13)

该式表明,当标的资产价格(S1,S2)不同时为0时,期权持有者的收益值为max(max(G1(I1),G2(I2))-K,0);若(S1,S2)当中有1个为0,或者(S1,S2)都为0时,期权持有者将变成零收益,此时该期权就丧失了本身持有的价值,期权投资者就不会对该类期权产生兴趣,更没必要去讨论定价问题。

2.2 模型的求解

(14)

(15)

(16)

(17)

(18)

即,当i=j=1,2时,式(17)(18)等式成立。

那么把式(14)～(18)代入式(5),进一步可得到式(19),如下:

(19)

为使式(19)便于讨论和计算,令

(20)

式(19)可进一步简化为

(21)

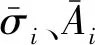
(22)

解这个方程要使用时间平均而不是时变系数,进一步可得到

(23)

接下来介绍累积概率函数。N2(Zi,Yi)表示二维变量的累积标准正态概率函数,矩阵Zi可定义为

(24)

且有

(25)

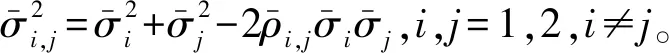
(26)

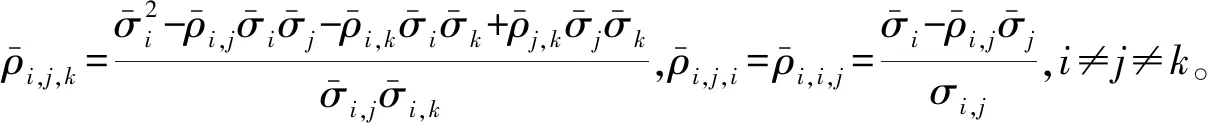
综上所述,期权价格可以表达为

U(v1,v2,T)=S1exp(-TA1)N2(Z1,Y1)+S2exp(-TA2)N2(Z2,Y2)-Kexp(-rT)N2(Z3,Y3)。

(27)

从上述的证明过程和求解过程可以看出,对两资产期权进行定价,要构造出标的资产价格满足的偏微分方程,然后通过偏微分方程的证明和求解过程得出期权定价的方法。接下来对上述结果进行数值计算,对相应的参数进行赋值,先计算出期权的价格,然后再讨论各参数对期权定价结果的影响。

3 数值分析

通过对MFBM模式下所研究的偏微分方程的构造与求解,可以看出对于2种标的资产价格所构成方程的计算比较复杂,但当使用泰勒展式、变量代换、降低维数后,还是可以将其进行证明并求解,说明构造标的资产的偏微分方程可以对多资产(含2种及以上标的资产)期权定价提供新思路。

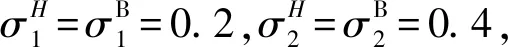
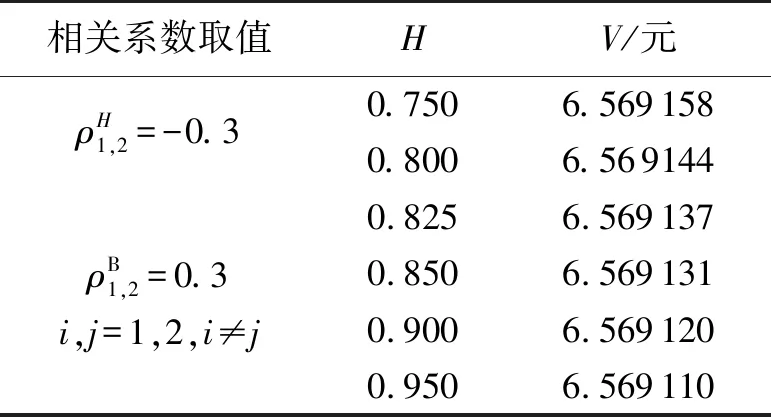
表1 MFBM模型中指数H对期权价格的影响Tab.1 Influence of index H on option price in MFBM model

由表1可知,如果其他参数不变,只考虑H的变化:当H值变大时,V值会变小,说明改变参数对期权价格有很大的影响,在MFBM模式下讨论期权价格,H有着不可忽视的作用;另外,H值越接近1,V值受其影响程度越小。因此,H值的选择要根据实际情形确定,才会使得期权持有者的收益最大化,这也是所有期权持有者的共同目标。

此外,MFBM模型中包含了多个参数,都有重要作用,因此对这些参数的讨论也很必要。假设H值不变,H=0.75,到期日取为半年(T=0.5a),其他参数变化对V值的影响如表2所示。

表2 其他参数对期权价格的影响Tab.2 Influences of other parameters on option prices

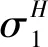
4 结论

研究两资产期权的定价问题,首先回顾布朗运动和分数布朗运动的相关定义;然后将布朗运动和分数布朗运动进行线性组合,构造出分数布朗运动模型;接着在该模型下构造含有2个自变量的偏微分方程,并对方程进行证明与求解;在求解过程中运用泰勒展式对其进行证明,进行变量变换,以使其维数降低,便于计算;最后,进一步进行数值模拟,分析H及其他参数对期权定价的影响,并做出相应的解释。结果表明,在MFBM模式下两资产亚式期权定价是合理、有效的,对多资产期权定价的相关研究有所帮助。

基于MFBM模型对亚式期权模拟定价的研究不再考虑单资产标的价格的定价问题,而是考虑了2个资产的定价问题,并且分析了各参数对期权价格的影响,在后续的研究中将会考虑将该模型推广到多个资产定价问题求解,并把这种模型应用于难以得到解析解的美式期权定价领域。