函数型数据下广义分位数回归模型的PM2.5分析

郑 禹,罗双华,周锦涛

(西安工程大学 理学院,西安 710600)

近几十年来,函数型数据分析(functional data analysis,FDA)应用范围愈加广泛。它是以曲线和图像形式储存、以函数形式表达的复杂类型数据,具有函数性、时间序列和截面数据等重要特征。其概念是由加拿大统计学家Ramsay[1]在1982年首次提出,解决了传统统计方法的参数限制,因而吸引了越来越多学者和专家的关注与研究,在国内外取得了极大的发展和应用。Wang等[2]研究了随机缺失函数型数据的非参数逆概率加权估计;Yu等[3]利用函数型数据对斜率函数进行拟合并应用在电力消耗数据中;Sang等[4]提出了函数型单指数分位数回归模型;Du等[5]提出了函数型数据主成分分析与复合分位数结合的方法;Yu等[6]将多项式样条与函数型数据、复合分位数结合,并应用于光谱数据集;严明义[7]系统地给出了函数型数据的研究意义、分析方法、模型构建及算法总结;米子川等[8]将函数型数据和函数型主成分分析用向量的思想进行解释;孟银凤等[9]将中国19类行业年平均工资进行函数型数据分析,采用聚类分析、函数型主成分分析等方法描述平均工资增长情况和现状;孙鸣茜[10]将多元分位数回归拓展到函数型数据分析中,并使用单纯形法和贝叶斯估计得到不同τ值下的函数曲线。可见函数型数据分析在国内外已经取得了大量的理论和应用研究成果。

另外,数据大多存在异方差、波动幅度较大、尾部特征不便描述等特征,传统线性模型不能解决此问题,所以众多学者将分位数、复合分位数引入函数型数据的分析中来代替最小二乘估计,但少有文献将广义分位数与函数型数据结合分析。朱佳等[11-12]将函数型数据与广义分位数回归相结合,对广州市2005-2017年PM2.5数据进行解释分析、拟合预测。PM2.5作为大气污染的一大主要污染源,是导致雾霾的关键因素,会对人体尤其是肺部带来极大伤害。随着人们对健康的重视程度逐渐提高,对PM2.5实时浓度的监测、预测、决策十分重要。借鉴文献[11]的分析方法,新引入温度、湿度2个协变量,探究其是否对PM2.5浓度有显著影响。将1年中每天的PM2.5数据转化为1条函数曲线,以曲线为最小单元进行后续分析,以期探索出能够拟合PM2.5历史数据,并能较为准确预测PM2.5未来数据的新模型,从而为大气污染的防范、治理提供依据。

1 模型与方法

1.1 函数型数据分析

进行函数型数据分析的前提是将离散数据转换为函数型数据。将离散的数据点拟合为光滑的函数,这时需要用到基函数来对数据进行修匀,即光滑处理。例如:

{xn(t):t∈[T1,T2]},

(1)

其中,xn(t)∈R为连续函数,t∈[T1,T2],n=1,2,…,N,N表示观测数据的个数。

统计中对数据进行修匀的技术很多,较为常用的方法有插值法、最小二乘法、加法光滑法和基函数法等。对于基函数的展开,选用B样条基函数为代表,基本思想是:从希尔伯特空间中选取1组基函数,它们是一些相互独立的函数集,通过赋给每个基函数不同的权重,可以对任何函数进行拟合。假定需要拟合函数为x(t),选取k个基函数:

φk(t),k=1,2,…,K,

(2)

使得

(3)

(4)

(5)

其中,K为B样条基函数的次数。得到B样条基函数之后,由式(6)可求解权重系数ck:

(6)

求解式(6)得

ck=∑φk(Tj)xT(j)∑φk(Tj)[∑φk(Tj)∑φk(Tj)T]-1。

(7)

1.2 函数型数据主成分分析

函数型数据主成分分析(functional data principal component analysis,FPCA)是函数型数据分析中最常见的降维方法,是传统主成分分析的推广,致力于将函数从高维空间转到低维空间,即用较少的基函数来表示原高维基函数,以将复杂数据简单化而得到广泛应用。目前用主成分分析方法处理函数型数据有2个方向,一是样本为N个P维向量的多元函数型数据,此时向量中每个元素为1个区间内的函数而非数值;二是样本为N的单变量函数型数据,每个研究个体只有1条函数曲线。与传统的主成分分析不同,单变量函数型数据在不同时间点的观测值可能具有一定的相关性,即它的目的是处理时间上的相关性,是样本值在时间上的协方差函数,故FPCA得到的主成分是函数形式。

(8)

其中,aij(第i个样本值在第j个主成分特征函数上的投影)为主成分得分,i=1,2,…,n,j=1,2,…,q;u(t)为均值函数,选择截断q,使得

(9)

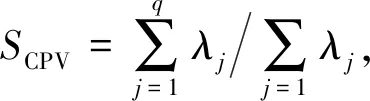
为了寻找主成分权重函数(特征函数)v1(t),v2(t),…,vq(t)和主成分得分aij,通过方差最大法,有

(10)

(11)

可以证明主成分权重函数为样本协方差函数的特征函数,如下所示:

(12)

其中,样本协方差函数为

(13)

最后求得主成分权重函数v1(t),v2(t),…,vq(t),以及主成分得分aij,i=1,2,…,n,j=1,2,…,q。

1.3 广义分位数回归模型

与分位数回归类似,广义分位数回归可以弥补最小二乘法要求误差均值为0、方差相同的限制。将传统最小二乘法的1条曲线,扩展为不同τ值对应的1组曲线,能够对数据包含的信息进行更全面地展示,也可以刻画随机变量的分布特征,本质上是分位数的改进。与分位数回归的绝对损失函数相比较,广义分位数回归的优势在于其损失函数是可微的,即损失函数由绝对损失变成平方损失,零点由不可导变为可导,曲线由不光滑变为光滑,并在计算效率上拥有更大优势,因此又被称为期望回归。相关理论最早由Newey与Powell[13]在1987年提出,通过非对称最小二乘回归来求解期望回归。对于1个随机变量Y,其分布能被函数Fy(y)刻画,对于0到1内任意的1个分位点τ,Y的分位数函数为

(14)

广义分位数函数的解定义为下式的最小化:

(15)

此时损失函数定义为

(16)

其中,I为1个示性函数;f(·)为来自函数集合F关于协变量X的非参数函数。

2 实例分析

2.1 数据说明

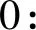
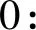
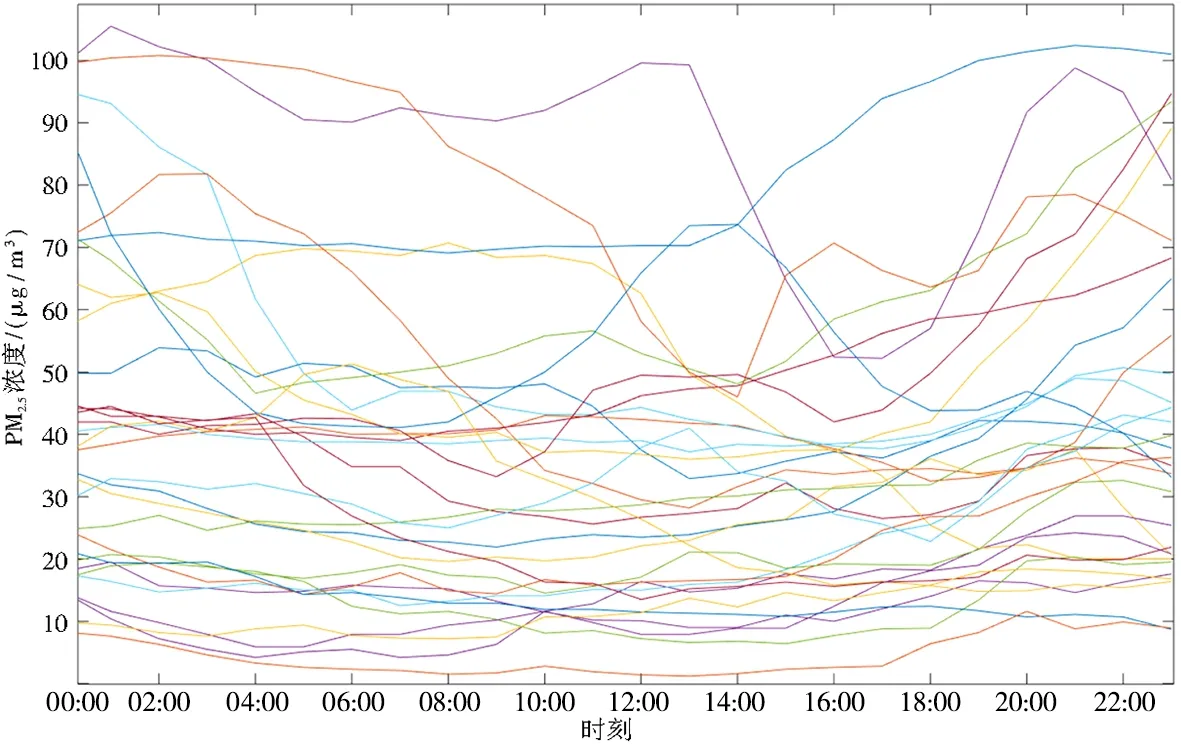
图1 2023年1月广州市PM2.5实时浓度Fig.1 Real time PM2.5 concentration in Guangzhou in January 2023

每条线表示1天24h内的PM2.5浓度的波动、走势。图1为2023年1月广州市PM2.5实时浓度图。由图1可知,广州市1月PM2.5实时浓度约为0～100μg/m3,分布较为均匀。图2为2023年1-12月广州市PM2.5实时浓度图。由图2可知,广州市2022年PM2.5实时浓度约为0～120μg/m3,并且波动幅度较大:高浓度大部分集中在冬季出现,夏季的浓度偏低。下面对以上数据进行季节分解、广义分位数回归以及在广义分位数下的函数型主成分分析。

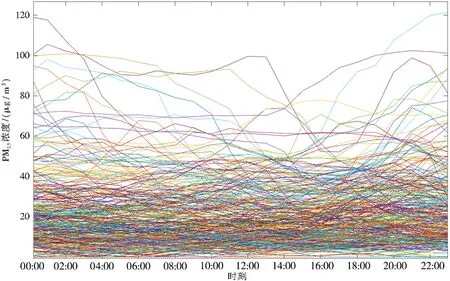
图2 2022年1-12月广州市PM2.5实时浓度Fig.2 Real time PM2.5 concentration in Guangzhou from January to December 2022

2.2 季节分解

图3为季节分解图。由图3可知,冬季PM2.5浓度最高,其次是春季、秋季,夏季PM2.5浓度相对低且变化平缓,出现很明显的季节差异,推测可能与湿度、温度、风级等因素有关,需对其进行季节分解。将PM2.5浓度数据整理为时序数据带入R软件进行季节分解,得到季节项、趋势项、随机干扰项。

图3 季节分解Fig.3 Seasonal decomposition

进行季节分解的目的是对随机干扰项进行广义分位数回归。之后分别对季节项、趋势项、拟合后的随机干扰项进行预测,再求和得到最终预测值。分解公式如下:

(17)

其中,Si,t表示第i天第t时刻的季节项;Ti,t表示第i天第t时刻的趋势项;Ii,t表示第i天第t时刻的随机项;i表示观测的总天数;t表示24h中的某一时刻。通过季节分解可以将原始PM2.5浓度数据分解为季节项、趋势项、随机干扰项3项。

通过式(18)表示季节项:

Si,t=aT+bT+c1,tsin(2πi/366)+

(18)

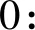
2.3 函数型广义分位数回归

由于PM2.5浓度数据波动幅度大、极有可能出现尖峰厚尾的特征,故对标准化后的PM2.5实时浓度数据进行广义分位数回归。通过文献调研与空气质量在线监测分析平台(http://www.aqistudy.cn),发现影响PM2.5的主要因素为:温度、湿度、风级。经过验证,这3个协变量的p值分别为px1=5.91×10-7,px2=1.02×10-6,px3=0.0278,均小于0.05,说明温度、湿度、风级这3个协变量对PM2.5浓度有显著影响,因此选择影响PM2.5的变量分别为:温度(x1)、湿度(x2)、风级(x3)。这里数据来源不同是由于2.1节只有PM2.5历史浓度数据,还需要在此平台中爬取3个协变量数据。

将数据整理后加载广义分位数R包,运行出广义分位数回归在不同τ值下的系数估计和区间(以τ=0.8为例),结果如表1所示。由表1可知,温度对广州市PM2.5浓度数据有显著的正影响:在其他因素不变的情况下,温度每升高1个单位,PM2.5浓度会升高2.6个单位;湿度对PM2.5也有正影响:湿度每增加1个单位,PM2.5浓度增加0.6个单位;风级对PM2.5浓度有显著负影响:在其他条件不变的情况下,风级每增加1个单位,PM2.5浓度下降2个单位,这与真实情况相符。因此,风是减少PM2.5浓度的主要因素,如果想降低城市PM2.5浓度,应该注重城市结构通风性的规划。分位数回归曲线由式(19)表示:

表1 τ=0.8系数估计与区间Tab.1 Estimated and interval of τ=0.8 coefficient

(19)

同理得到其他分位数回归曲线,如图4所示,由上到下分别为τ=0.9,…,τ=0.1。由图4可知,不同的τ值形成了1个区间,这使得对PM2.5浓度这一指标的描述更多元、更全面。将得到的各个曲线与原始数据进行相关性分析,选择相关性最高的1条曲线,由结果可知τ=0.8时的分位数回归曲线与原始数据相关系数最高,为Scor=0.6531246,因此在τ=0.8的基础上进行分析。

图4 不同τ值对应的Y函数曲线Fig.4 The curves of Y function of different τ values

2.4 函数型主成分分析

对广州市2022年PM2.5数据进行函数型主成分分析得到4个主成分。第1、2、3、4主成分分别提供了84.7%、7.9%、3.6%、1.7%的贡献率,由于前4个主成分的累积贡献率达到97.9%,所以选取4个主成分即可,即把数据降为四维数据,使用前4个主成分来反映原高维数据,以达到主成分分析的初衷:降维和解释。

(a) 第1主成分 (b) 第2主成分 (c) 第3主成分 (d) 第4主成分图5 主成分特征函数曲线Fig.5 Principal componentcharacteristic function curves

2.5 模型估计与预测

选取置信水平α=0.05,置信度为1-α=0.95,将PM2.5预测曲线与真实曲线对比,结果如图6所示。由图6可知,预测值与真实值拟合良好,且全部在95%置信区间内,这意味着真实值将有95%的概率落在置信区间内。

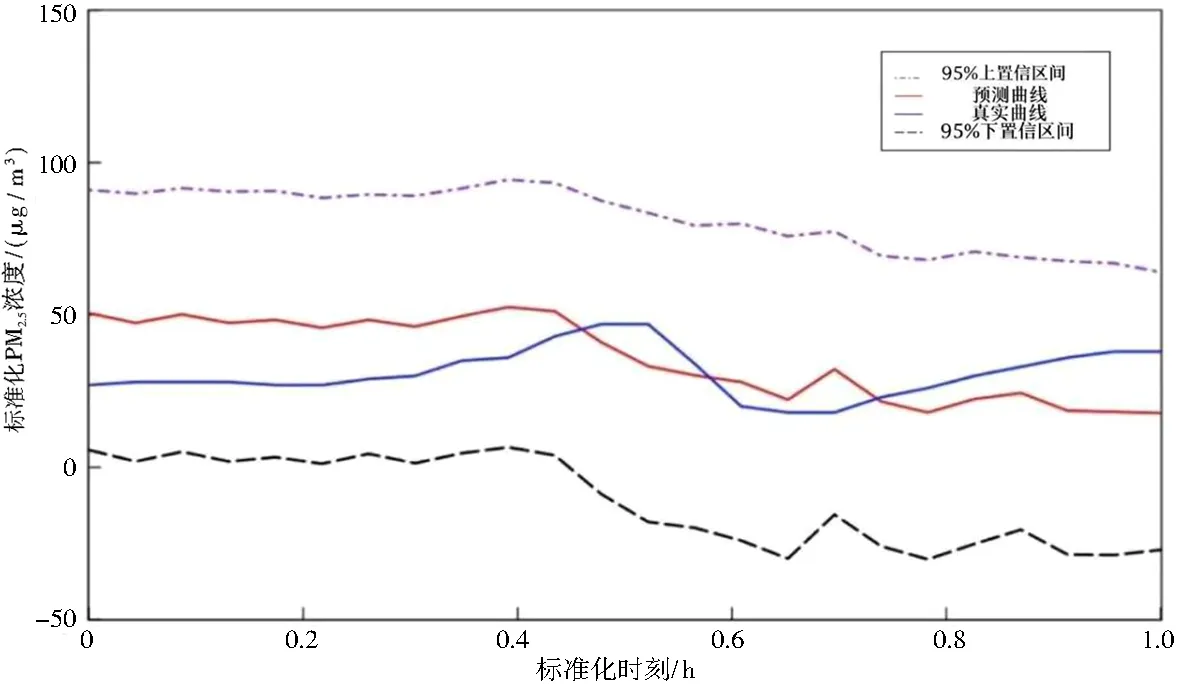
图6 PM2.5未来24h各类曲线Fig.6 PM2.5 curves in the next 24 hours

3 结论

在将离散数据转为函数型数据的研究基础上,先对数据进行光滑处理,并利用基函数展开求出系数,再引入广义分位数回归,得到不同的广义分位数函数曲线,使得当数据存在显著异方差或出现尖峰厚尾、偏态分布等情况下能有更好的稳健性。此方法与传统线性回归相比,得到的信息更稳定、全面、丰富,效果更好。以广州市PM2.5浓度数据为实例,新引入温度、湿度等协变量,得到温度、湿度、风级的p值均小于0.05,说明均对PM2.5浓度有显著影响。再利用4个主成分反映复杂且高维的PM2.5实时浓度,可以解释原始数据97.9%的方差。虽然PM2.5浓度波动幅度大,对其预测较为困难,但所用方法使得PM2.5的预测值与真实值拟合较好,真实值曲线全部在95%置信区间内。该研究能为人员出行、PM2.5防控等提供一定指导。