基于改进KNN的离散型车间物流车定位系统

朱 萌,李敬兆,李化顺,石 晴

(1.安徽理工大学 人工智能学院,安徽 淮南 232001;2.安徽理工大学 电气与信息工程学院,安徽 淮南 232001;3.淮北合众机械设备有限公司,安徽 淮北 235000)

中国工业5.0概念的提出,推动了工业产业数字化发展。近年来,制造车间数字化转型已成为未来车间建设的趋势。与数字化制造车间相关的应用多数离不开定位技术的支持。随着网络通信、全球定位系统(global positioning system,GPS)等一系列技术的飞速发展,定位技术的精确度和速度得以大幅度提升。然而,在车间内由于室内环境条件限制,阻碍了接收来自室外GPS的位置数据,使得位置精确度大大降低。因此,高精度的室内定位系统具有极高的科学研究关注度和社会应用价值。

目前,主流的室内定位算法大致分为两类:测距和非测距的空间定位算法[1]。前者是利用目标位置和参考位置之间测得的角度或距离,通过计算判断出目标点的位置,主流算法包括接收信号强度指示(received signal strength indication,RSSI)[2]、到达时间(time of arrival,TOA)[3]、到达时间差(time difference of arrival,TDOA)[4]等方法;而后者是利用网络拓扑结构信息来判断测量目标点的位置,主流算法包括距离向量算法[5]、位置指纹定位算法[6]。相较于测距定位算法,非测距定位算法具有功耗小、成本低且易实现等优点。

位置指纹定位算法是由离线和在线两阶段完成的[7]。离线阶段的任务是实现对每个参考位置不同的无线接入点(access point,AP)采集RSSI值,构建指纹信息库。在线阶段的任务是实现对目标位置的不同AP进行RSSI值采集、匹配和定位。目前,位置指纹定位的方法包括贝叶斯法、近邻法(nearest neighbors,NN)和K近邻法(K-nearest neighbors,KNN)等。向文平等[8]提出熵定权KNN算法,利用熵权法从特征数据自身调整权值,改进KNN需要人为设定权值的问题,提高了定位的稳定性和精确度,但是自适应K值在指纹库参考点稀疏区域会引入定位误差。Liu等[9]使用RSSI的平均值和AP的方差作为特征向量,利用AP和网格相关性决定算法权重,优化加权KNN算法,提高了算法精确度,但只与加权K-近邻算法(weightedK-nearest neighbors,WKNN)进行对比,算法准确性不高。吴虹等[10]在传统KNN算法的基础上,在离线阶段使用采集调频(frequency modulation,FM)和地面数字多媒体广播(digital terrestrial multimedia broadcast,DTMB)联合信号的方法构建指纹库,达到优化算法的目的,实现了良好的定位准确度,但算法采用的信号具有不稳定的特性。孙建强等[11]在Sugeno型模糊推理和距离信息中加入KNN算法,定位误差维持在10cm左右,但该算法对实验环境具有一定的要求。

传统的位置指纹算法无法解决离散型车间物流车定位精确度较低、定位速度较慢、Wi-Fi特征维度不确定等问题。因此,设计了基于余弦夹角改进KNN定位算法(cosine angle basedK-nearest neighbors,CA-KNN)的离散型车间定位系统。该系统基于M5Stack模块开发,依赖于Wi-Fi网络。系统设计断线重连机制,并利用余弦夹角优化KNN算法,通过余弦夹角划分样本空间区域,并根据余弦夹角和权重K筛选最终位置预测结果。

1 位置指纹定位算法

1.1 KNN算法

作为分类算法,KNN算法最为常用,其优势包括易于实现、无需训练等。KNN算法首先计算目标位置到所有参考位置的距离,用来作为2个节点之间的相似程度。通常采用欧式距离计算,公式为

(1)

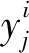
该算法选择距离目标位置最近的K个参考节点,利用合适的决策函数,得到最终目标位置的预测结果。决策函数一般有多数表决法、回归平均值法等。

1.2 基于CA-KNN的位置指纹定位算法

针对原始KNN算法应用于离散型车间时无法解决Wi-Fi特征维度不确定且定位精确度不高的问题,提出CA-KNN算法。该算法利用余弦夹角优化样本数据库,减少数据匹配时间,然后利用余弦夹角代替传统KNN算法中使用欧式距离进行相似度选择。基于CA-KNN的位置指纹定位算法流程如图1所示。由图1可知,该算法包括以下流程:

图1 基于CA-KNN的位置指纹定位算法流程Fig.1 The process of location fingerprint localization algorithm based on CA-KNN

1) 离线阶段。首先,按照车间布局,划分多个参考定位区域,然后对各个参考区域进行编号。由于Wi-Fi信号在每个参考区域有很强的波动性,因此,为了使指纹数据库中每个参考区域的特征信息可以更加准确,将对每个参考区域进行重复采样。

假设车间划分参考位置有m个,Wi-Fi热点有n个,每个参考位置重复采样t次,那么构成的指纹数据库组成如下所示:

(2)

其中,Pn为互联网协议(internet protocol,IP)地址;Fn为RSSI值。

2) 在线阶段。该阶段主要利用CA-KNN算法进行指纹数据在线匹配。指纹数据库中大量的样本数据会导致定位速度下降,因此利用余弦夹角划分样本空间分布区域。首先计算样本数据和坐标轴之间的余弦夹角,并按0.1的区间差值将样本空间划分为不同的区域,然后计算物流车当前位置和坐标轴之间的余弦夹角,并判断该位置的归属区间范围。

在此引入Wi-Fi标签匹配机制。传统的KNN算法只能在Wi-Fi特征维度确定不变的情况下实现;然而,在离散型车间中,Wi-Fi的特征维度是不确定的;因此,系统利用Wi-Fi标签匹配机制解决此问题。匹配机制如图2所示。

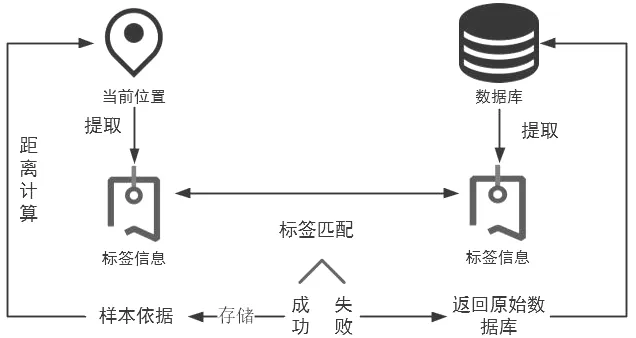
图2 Wi-Fi标签匹配机制Fig.2 Wi-Fi tag matching mechanism

由图2可知,将当前位置采集的Wi-Fi标签信息与该区间的样本数据标签信息进行匹配,筛选出与当前位置采集的Wi-Fi标签信息相同的样本数据作为最终计算距离的样本依据。将车间进行区域划分、编号后,物流车可经过的区域编号是固定且已知的。为提高定位精确度,利用余弦夹角和欧式距离相结合的方法计算目标位置预测结果。

在得到当前位置归属区间范围后,首先利用余弦夹角公式计算该位置与该区间范围内样本数据的余弦夹角,计算公式为

(3)

其中,α为数据在样本空间的向量;β为坐标轴在样本空间的向量;·表示向量间点乘。

得到区域编号、样本特征值和余弦夹角组合信息N,如下所示:

(4)

其中,tp为第p个样本归属的区域编号;Fp为第p个样本的特征值;rp为目标位置和第p个样本之间的余弦夹角。

接着,取余弦夹角较大的前k组的组合信息特征值与物流车当前位置的特征值进行欧式距离计算,计算公式为

(5)

其中,R为物流小车当前位置的Wi-Fi特征值;Fi为组合信息中第i组的特征值。

经过距离计算得到区域编号和距离的组合信息E,如下所示:

(6)

其中,tk为第k个样本归属的区域编号;dk为目标位置和第k个样本之间的欧式距离。

最后,从k个组合信息中选择距离最近的区域标签作为最终目标位置预测结果。

2 系统设计

系统流程如图3所示。由图3可知,该系统基于M5Stack模块运行,离线阶段采集每个参考位置基于Wi-Fi的特征信息,筛选指纹数据,构建指纹信息库;在线阶段利用CA-KNN定位算法计算定位结果,最终利用消息队列遥测传输(message queuing telemetry transport,MQTT)协议将定位结果发送到用户终端。

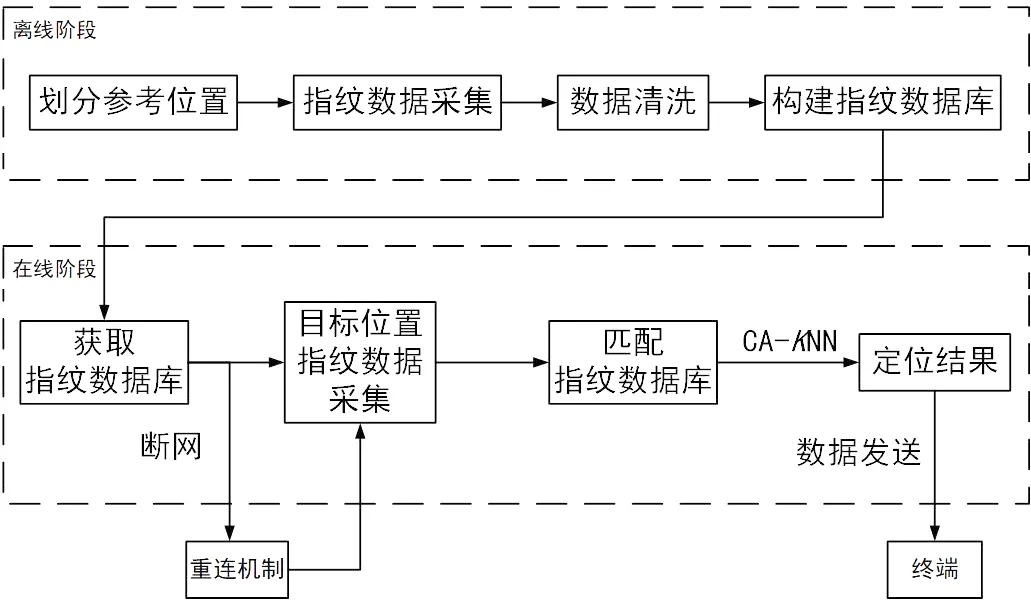
图3 系统流程Fig.3 System flow

2.1 M5Stack模块

基于乐鑫系统平台32(Espressif system platform 32,ESP32)和Micro Python开发的M5Stack微控制模块具有轻便、易操作等特点,因此适用于智能工厂、数字化车间等一系列工业化环境开发。M5Stack模块结构如图4所示。

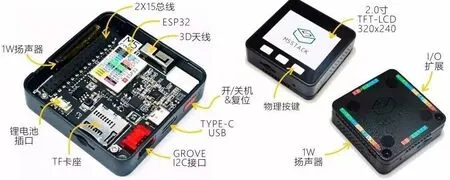
图4 M5Stack微控制器模块结构Fig.4 M5Stack microcontroller module structure

由图4可知,M5Stack模块包括1个2.0寸的液晶显示器(liquid crystal display,LCD),用以显示当前定位位置;物理按键可用于进行指纹数据采集;内置存储器可以存储采集的指纹数据;ESP32可作为系统运行所需的底层平台。综上所述,M5Stack模块较适合成为室内定位系统的载体。

2.2 数据清洗

由于车间网络环境复杂,网络易于发生变化。当网络环境发生波动时,在采集指纹数据的过程中可能会采集到与当前位置网络环境基数相差过大的数据——突变数据。该数据的产生会导致定位结果不准确,因此有必要在进行定位计算之前先进行1轮指纹数据预清洗。数据清洗过程如图5所示。

图5 数据清洗Fig.5 Data cleaning

由图5可知,首先将指纹数据库中的每个样本当作拟目标位置,与指纹数据库中其他样本进行距离计算,得出该样本在数据库环境下的位置信息;然后将得到的位置信息与该样本在指纹数据库中的位置信息进行比较,若不同则认为该样本为突变数据;最后将所有的突变数据移出指纹数据库。数据清洗环节的设计可以有效减少定位时间且提高定位精确度。

2.3 重连机制

考虑到车间可能会有断电、断网等突发事件发生,会导致系统与终端断连,即使在网络恢复后仍无法连接终端,需要手动重连的问题,系统增加了断线重连机制;该机制过程如图6所示。

图6 用户端重连机制Fig.6 Client reconnection mechanism

由图6可知,系统首先检测网络连接情况,当检测到网络连接失败无法向终端发送数据时,系统将转入断线重连机制;当系统运行过程中网络发生中断时,系统也会立刻转入断线重连机制;当系统转入断线重连机制后,系统将以每5秒1次的速度向终端发起连接请求,如连接成功则转回到主系统工作,否则继续发送请求。

3 实验及结果分析

3.1 实验场地及布局

为验证提出的CA-KNN车间物流车定位系统的效果,选择安徽淮北合众机械制造车间作为实验环境,获取指纹数据。该车间包括堆料区、作业区和几段较长的过道。车间区域划分如图7所示。

图7 车间区域划分Fig.7 Workshop area division

1) 指纹数据的采集及处理。由图7可知,按照图中所示的车间区域划分,每个区域分别进行指纹数据采集,每区采集150条数据;为减小Wi-Fi信号在室内的不稳定性,在每个区域按4个朝向平均分配采集数据。

2) 车间定位系统的部署及效果。将M5Stack模块部署在车间物流车上,对定位效果进行测试。首先测试模块在目标位置的定位准确性。将物流车移动到目标位置,车间大屏即刻显示出物流车当前所在的目标位置。车间定位系统部署及最终定位效果如图8所示。

(a) M5Stack模块位置显示 (b) 车间大屏显示小车位置图8 物流车定位效果Fig.8 Positioning effect of logistics vehicles

由图8可知,小车在位置41时的定位情况。当小车移动到目标位置时,系统读取当前位置的Wi-Fi特征值,并且与系统数据库进行计算,得出小车当前实际定位。小车装载的M5Stack模块显示出当前小车的Wi-Fi信息、Wi-Fi特征值和所在位置(见图8(a)),车间大屏即刻显示出小车当前所在位置(见图8(b))。

3.2 算法验证

安徽淮北合众机械制造车间已覆盖多个无线Wi-Fi,具体位置未知。测量过程中使用M5Stack模块进行指纹数据采集。对划分区域分别采用KNN、WKNN[12]和CA-KNN算法进行测量比较,设定K值为6,指纹数量为400,选取30个定位测试点,每个算法在各个测试点的定位误差如图9所示,定位误差对比结果如表1所示。

表1 不同算法在各测试点的定位误差对比Tab.1 Comparison of positioning errors of different algorithms at test points

图9 不同算法在各测试点的定位误差Fig.9 Positioning error of different algorithms at test points

由图9可知,相对于另外2个定位算法,CA-KNN算法定位误差有明显地降低,这是因为在进行室内定位时,使用余弦夹角结合欧式距离来计算与当前位置最相似的K个参考点,能够更准确地确定待测位置,即CA-KNN算法利用余弦夹角大大提高了定位精确度。由表1可知,CA-KNN算法在各个测试点的最小误差只有0.089m,平均误差只有0.114m;WKNN算法最小误差为0.104m,平均误差为0.129m;而KNN算法最小误差达到0.134m,平均误差达到0.154m,相较于KNN算法,CA-KNN算法平均误差降低了0.040m。

指纹数量的不同也会对定位精确度产生影响[13]。因此,设定K值为6,CA-KNN、WKNN、KNN算法在不同指纹数量下的定位精确度曲线如图10所示,定位精确度对比结果如表2所示。

表2 不同算法在不同指纹数量下的定位精确度对比Tab.2 Comparison of positioning accuracy of different algorithms in different fingerprint numbers

图10 不同算法在不同指纹数量下的定位精确度Fig.10 Location accuracy of different algorithms in different fingerprint numbers

由图10可知,随着指纹数量的增大,各个定位算法的定位精确度也在不断提升,这是因为定位样本依据的丰富程度会影响定位精确度。从曲线走向来看,CA-KNN定位算法在指纹数量为450时定位精确度达到最高,随后趋于平稳;这是因为随着样本数量增加,精确度在上升,但当样本到达一定数量后,精确度的增长会变得缓慢。由表2可知,CA-KNN算法的定位精确度最高可达92%,WKNN算法的定位精确度最高为77%,而KNN算法的定位精确度最高只有67%。但随着指纹数据量增大,M5Stack模块开始出现开机加载速度变慢、数据读取速度下降的问题。因此,最终定位区域的样本数量需要综合考虑定位需求和定位成本来决定。

K值的不同也会对定位精确度产生影响[14]。因此,设定指纹数量为400,CA-KNN、WKNN、KNN算法在不同K值下的定位精确度如图11所示。

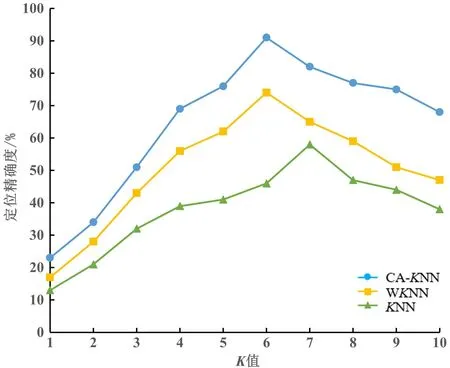
图11 不同算法在不同K值下的定位精确度Fig.11 Positioning accuracy of different algorithms under different K values

由图11可知,随着K值逐渐增大,各个定位算法的定位精确度也在逐步上升,CA-KNN定位算法在K值为6时定位精确度达到最高。当K的取值大于6时,精确度却有所下降,这是因为随着K的取值增大,相似性较低的样本也随之增多,从而使得定位精确度下降。

4 结论

针对车间Wi-Fi特征维度不确定、定位精确度较低等问题设计了基于余弦夹角改进KNN定位算法的车间物流车定位系统。该算法使用余弦夹角划分样本空间坐标,优化样本数据库,提高数据匹配速度;然后利用余弦夹角和欧氏距离组合的方法作为决策函数,提高定位结果精确度。实验结果表明,对比传统的KNN和WKNN算法,在相同的实验环境下,在各个测试点改进的CA-KNN算法优于以上算法,在测试点的最小误差为0.089m,最大精确度为92%,相比较于传统的KNN算法,平均误差减少了0.040m,最高精确度有明显提高。但由于系统依赖于M5Stack模块,在数据量过大的情况下有加载速度下降的缺点,因此响应速度有待进一步提高。