具有Beddington-DeAngelis功能反应函数的May-Nowak模型的全局动力学分析
刘丹丹,刘洪燕,蒋 敏
(贵州民族大学 数据科学与信息工程学院,贵阳 550025)
0 引言
在免疫学理论中,著名的May-Nowak微分方程模型很好地描述了病毒感染模型的动力学基本特征。首先,回顾一下May-Nowak常微分方程模型[1]:
(1)
其中,β1、k、r、d1、d2、d3为非负常数;函数u=u(t)、v=v(t)、w=w(t)分别表示t时刻未感染细胞、受感染细胞、病毒颗粒的数量;r代表健康细胞u的产生速率;ut、vt、wt分别表示u、v、w在时间上的变化。通过对模型进行深入的定性分析[1-3],知道基本再生数R0在研究系统的大时间行为过程中起到非常关键的作用,其生物意义表示在传染病发病初期(即所有人均未感染时),1个感染者在其平均患病时间内可传染的人数[4]。而系统(1)的基本再生数为R0=β1kr/(d1d2d3),当R0≤1时,病毒颗粒无法传播,系统恢复到无感染状态;当R0>1时,病毒颗粒进行传播,系统将收敛到平衡态,相关结果可参考文献[2,5-6]。
但是,系统(1)没有考虑空间效应,因此受到经典的Keller-Segel趋化模型启发,Hu等[7]提出了如下模型:
(2)
其中,∇·((u/(1+u)α)∇v)表示交叉扩散项。研究人员证明了当n=1,α>2/3和当2≤n≤4,α>(1/2)+(n2/(6n+4))以及当n≥5,α>n/4(n表示空间维数)时解的全局有界性。Winkler[8]优化了参数α的取值,得到了当n=1,α>-1和当n={2,3},α>(n-2)/(n-1)时解的有界性。黄金凤[9]证明了当(n-1)/n<α<1,且初始值(u0,v0,w0)足够光滑时解的全局有界性。接着,Bellomo等[10]考虑了如下模型:
(3)
受到文献[7,10]的启发,研究具有Beddington-DeAngelis型功能反应函数的模型,如下所示:
(4)
(5)
其中,
Du,Dv,Dw,a,α,di(i=1,2,3),β(x),h(x)>0,b≥0,
(6)
趋化敏感函数为
f(s)=(1+s)-α,s,α>0,
(7)
转化项函数满足
g(s)=βs/(1+as+bw),a,b,s,β>0,
(8)
基本再生数为
R0=βh/(ad2d3)。
(9)
研究模型(4)解的全局有界性和渐近行为,得到的结果如下:
定理1设Ω⊂n(n≥1)为光滑有界域,条件(6)成立,初值(u0,v0,w0)满足
(10)
并且
α>max{n/4,1/2+(n(n+2)/(6n+8))},
(11)
模型(4)具有1个全局经典解
且存在常数C>0使得对所有t>0,有
后文中C均表示大于0的常数,但在不同公式中取值各不相同,省去下标。
定理2设Ω⊂n(n≥1)为光滑有界域,条件(6)成立。如果
R0<1,
(12)
并且
β/(ad2d3)<1,
(13)
则对条件(10)和任意的t>0,当t→∞时,模型(4)的解满足
(14)
1 准备工作
下面给出模型(4)解的局部存在性及一些准备工作。
根据假设(5),可以找到常数L>0使得
0 (15) 接下来证明全局有界性。 (16) 引理2模型(4)的解满足 (17) (18) (19) 对于所有t∈(0,Tmax)成立。 证明将模型(4)第2个方程加到第1个方程后再关于x积分可得 对于t∈(0,Tmax),由常微分方程的比较原则可得式(19)。 后文中M均表示大于0的常数,但在不同公式中取值各不相同,省去下标。 证明根据常数变易法公式,由Neumann Laplace热半群的正则估计[11]可知,存在常数k1>0,使得对t∈(0,Tmax),有 引理4假设条件(6)(9)(10)成立,p≥1和a∈[1,∞]满足(1/p+1/a)≤1和0<β≤p,且q1,q2∈[1,∞]满足 (1/p+1/a-1/n)<1/q1,(1/p+1/a-2/n)<1/q2, (20) (21) 其中,k1>0,由条件(20)可得式(21)。 引理5假设条件(6)(8)(10)成立,p≥1和a∈[1,∞]满足(1/p+1/a)≤1和0<β≤p,设p>n/4,如果存在常数M>0,使得 则存在常数C>0,使得 证明这个引理可以用与文献[7]引理2.6相同的方式来证明,此处省略细节。 推论1设Ω⊂n(n≥1)为光滑有界域,假设条件(6)(8)(10)成立,p∈(n/2,∞],如果 则对于常数M>0,存在常数C>0使得 引理6假设条件(6)(8)(10)成立。设q0∈[1,∞],p0∈[1,∞]满足 (22) 如果存在常数M>0,使得 则存在常数C>0,使得 证明这个引理可以用与文献[7]引理2.8相同的方式来证明,此处省略细节。 引理7假设条件(6)(8)(9)成立。设p0,p∈[1,∞]满足 (23) (24) 并且假设q∈[1,∞]满足1/q>(1/p-1/n),且存在常数M>0,使得 则存在常数C>0使得 (25) 则 证明在引理7中用类似于引理5的迭代方法,可得u和∇v的有界性。结合推论1,就得到模型(4)解的一致有界性。 引理8假设条件(6)成立,p>n/2,则满足条件(10)中的初值(u0,v0,w0)有非负函数 是模型(4)的解,并且 (26) 对任何p>n/2使得u,v,w在Ω×(0,Tmax)上是非负的。 引理9假设条件(10)成立,Du,h>0,d1>1/p,如果1≤p≤2α,则存在常数C>0使得对t∈(0,Tmax),有 (27) 该式成立。 证明将模型(4)中第1个方程两边同时乘以up-1,利用Young不等式[7]得 其中,t∈(0,Tmax);C=[(d1-1/p)·p/(p-1)]1-p·p-1·hp。又由p≤2α可知up/(1+u)2α≤1,因此式(27)成立。 引理10假设条件(6)(10)成立,如果p>1+(n(n+2)/(3n+4)),则存在常数C>0使得对t∈(0,Tmax),有 (28) 成立。 证明将模型(4)中第2个方程两边同时乘以v,可以得到 其中,常数θ1=2n(q-1)/q(n+4)∈(0,1)。由Gagliardo-Nirenberg不等式的条件θ1q<2得 1 引理11[12]假设条件(6)成立,(u0,v0,w0)满足条件(12),则存在常数C>0使得 (29) 对于所有t∈(0,Tmax)成立。 引理12假设条件(6)(10)成立,如果1+(n(n+2)/(3n+4)) (30) 证明由引理9至引理11可知 令b=2+((1-p)/2Du),l=max{d1,2d2,d3-1/b},则上式变为 其中C1为正常数,由比较原理即得式(30)。 定理1的证明设p∈((n(n+2)/(3n+4))+1,2α],由引理12可知存在C>0使得模型(4)的解满足 (31) 根据引理8,如果p>n/2,可以得到2α≥p>max{1+(n(n+2)/(3n+4)),n/2,((1-α)+n)/2,(1+(1-α)+)/(1+1/n)},化简即得α>max{n/4,1/2+n(n+2)/(6n+8)},(n∈N)。由引理12和推论2可以直接证明定理1。 0≤u≤H,0≤v≤H,0≤w≤H, (32) 下面先给出证明稳定性要用到的一些引理。 引理13假设R0≤1,条件(13)成立,记u*=h/d1并且令 (33) 其中r∈[βu*/d3,d2/k], (34) 则有 F′(t)≤-δE(t), (35) 其中,δ>0。 证明将模型(4)的第1个方程两边同时乘以(1-u*/u)再积分,应用Young不等式[7],有 (36) 再对模型(4)的第2个方程和第3个方程两边分别积分可得 (37) (38) (39) (40) 假设r>0满足 βu*/d3≤r≤d2, (41) 并且根据β/(ad2d3)<1,也可以取足够小的ε>0使得 ad2/β>1/(d3-ε), (42) 整理式(37)~(40)可得 由式(40)知d2-r≥0和rd3-βu*≥0,利用Young不等式[7]可以得到 因此式(35)成立, 由式(42)知δ=min{d1/A,(u*/(4DuDv))·(β/α)(ad2/β-1/(d3-ε)),(u*/(4DuDv))·(β/α)·ε}>0。 引理14假设R0<1和式(13)成立,则当t→∞时, (43) 证明由于(u,v,w)是模型(4)的全局有界解,由抛物方程的Hölder估计可知存在θ∈(0,1)和C>0使得对t>1,有 (44) 在文献[7]的基础上增加了Beddington-DeAngelis型功能反应函数,这使得模型更通用且切合生物场景。所做的工作在任意空间维数条件下进行,当初值(u0,v0,w0)、参数α满足一定的正则性和限制条件以及基本再生数R0<1时,利用Lp估计、Young不等式、Hölder不等式、Gagliardo-Nirenberg不等式和Neumann热半群理论以及构造适当的Lyapunov函数,证明了系统(4)解的全局有界性和渐近行为,进一步丰富了偏微分方程的理论基础。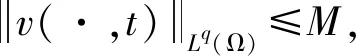




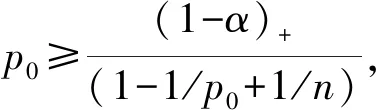
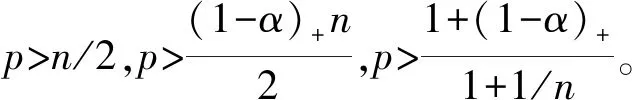

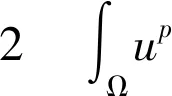
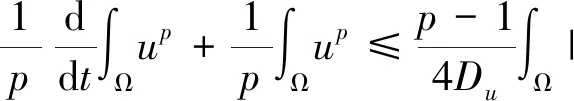
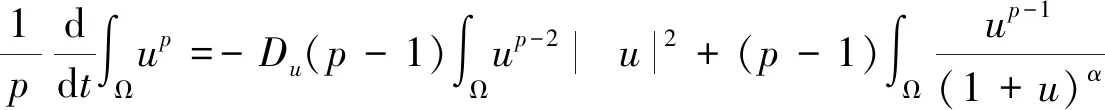





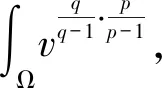


3 稳定性及定理2的证明

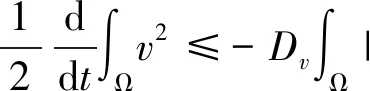


4 结论

