“赵州桥”中的传统数学文化
林琪瑜 张维忠

【摘 要】桥是表达中华优秀传统文化与数学文化的媒介,沟通人与自然的重要桥梁.基于赵州桥的历史文化,揭示了赵州桥中蕴含的数学与传统数学文化,让学生洞见古人智慧,实现今人与前人的对话,促进学生数学核心素养发展.
【关键词】赵州桥;传统数学文化;数学探究
成长至今的你走过多少桥?生活中的你又多少次用“桥”将世界联结?自古以来,桥是文人墨客们创作灵感之源,是人类最伟大的创造之一.它蕴含着建筑美、数学美、绘画美、文学美……而赵州桥是我国古代先人将人、自然、科学巧妙联系后创造的代表性杰作,充满了中华优秀传统文化与数学文化.在这里,让我们一起揭开“赵州桥”的神秘面纱,一同领略它的美,揭示其蕴含的传统数学文化及教育价值.
1 初闻“赵州桥”的故事
赵州桥(图1)坐落于河北省赵县洨河上,建于隋代公元605—618年间,由中国第一位桥梁专家李春建造.因赵县古称赵州而得名,后由宋哲宗赵煦赐名安济桥,并以之为正名.
隋朝赵县不仅是战略要地,还是南北交通的枢纽:北上可抵重镇涿郡,南下可达京都洛阳,但横亘在境内的“巨川”洨河对交通造成严重阻碍,于是巧工能匠李春受命负责设计这座大石桥.他周密考察自然环境,结合实际需要,在继承前人经验的同时,发挥智慧与才能,成功建造了这座举世闻名的赵州桥.这座屹立了1400多年的石桥,犹如一首千古绝唱,历久弥坚,它也是世界上现存年代久远、跨度最大、保存最完整的首创“敞肩拱”形单孔坦弧敞肩石拱桥.
“玉石栏杆圣人留,张果老骑驴桥上走,柴王爷推车轧了一道沟”的圣人与仙迹传说是游人津津乐道的有趣内容之一.相传著名工匠祖师鲁班为解决洨河两岸来往困难的问题,一夜之间建好了赵州大石桥,这一奇迹惊动了“八仙”之一的张果老.张果老想试一试这桥到底结实否,便在驴背的褡裢里一边装上了“太阳”,一边又装上了“月亮”,要在桥上走过.与此同时还请来了柴王爷推着载有“五岳名山”的独轮车.他俩一人骑着驴,一人推着独轮车就上了桥.不料桥被压得摇摇欲坠,鲁班急中生智跳下桥去,用手托住桥身东侧,这才使两位仙人顺利通过.
这“神仙斗法”的故事,还留下了后人“有迹可查”的仙迹:张果老的驴蹄印压出了圆坑窝;柴王爷推车过猛压出的膝盖印和车道沟(图2);以及鲁班托桥的手印.
2 探秘“赵州桥”中的数学
赵州桥长64.40米,跨径37.02米,拱矢7.23米,拱矢和跨度的比例大约是1∶5(图3).只用单孔石拱跨越洨河,由于没有桥墩,既增加了排水功能,又方便舟船往来.桥高比拱弧的半径要小得多,整个桥身只是圆弧的一段,这样的拱,也叫做“坦拱”.以此为拱桥的承重结构,可使在相同跨度情况下,大幅度地降低桥梁高度,使得桥面更加平缓,便于舟车人马通行.
赵州桥的石拱有28道拱券并列砌筑,每一拱券可独立成拱,便于后期修补.桥台基础为砌石浅基礎,基础宽度9.6 m,长度5.8 m,基础高度1.57 m,埋深2.0~2.5 m(图4).这样低拱脚、浅基础、短桥台的特征,使其桥体稳固坚实.虽然并列拱券结构易横向联系不足,需要通过护拱石、铁梁、腰铁等方式加强联系,但是赵州桥的拱脚仰角已然是基本达到最佳设计.
列出拱脚的水平推力和抗力相平衡的方程式:Tsin αtan φc+PpTcos α=K.
(其中,T为拱脚的轴向推力,α为拱脚的仰角,φc为基底综合摩擦角,Pp为基础侧面被动土压力,K表示安全系数)
当取Pp=0,K=1时,有tan α=1tan φc,可画出图5.
如图6,若拱脚的仰角α设计太小,则拱脚对基础的水平推力就会过大,不利于基础水平稳定;若拱脚的仰角α设计太大,则拱脚对基础的水平推力就会变小,但此时拱券的高就会增大,桥面愈发陡,不利于通行.而从上面的简单分析中,发现当拱脚的仰角α为40°时,基底综合摩擦角为50°,此时情况最佳,这便是赵州桥的拱脚仰角度数,可见这座石拱桥的设计充满着隋代尧山石匠的智慧与胆识!
谈及桥面平缓,这优美的曲拱,实际是用一块块直棱石料构造而成的,你是否心生疑惑了呢?直棱怎么会铺成一个圆弧曲拱呢?其实,这其中闪耀着数学曲中有直、化曲为直的思想光芒!
赵州桥的曲直与我们学的圆有什么联系呢?在推导圆的面积公式时,我们把圆分割成许多扇形,然后把这些扇形拼成接近矩形或平行四边形.分的扇形越多,扇形的弧就越接近直线,化曲为直,由此推导出圆的面积公式.公元3世纪北魏的刘徽提出的“割圆术”(图7),就体现了现代微积分的极限思想,即用圆内接正多边形的面积来逼近圆面积,也体现了曲直互化.他把极限的动态变化过程及其归宿描述得十分透彻和传神:“割之弥细,所失弥少,割之又割,以至不可割,则与圆周合体而无所失矣”(图8).用圆内接192边形的周长与直径之比作为“π”的近似值,得到了π≈3.14的世界首创.无独有偶,祖冲之利用圆内接正12288边形,得出π介于3.1415926与3.1415927之间,成为世界上第一个把π的准确值计算到小数点后七位的人[1].
3 “赵州桥”里的数学题
2013版浙教版“义务教育教科书·数学”九年级上册第三章“圆的垂径定理”节前语[2]就借赵州桥引入,并探索垂径定理:“我国历史上著名的赵州桥建于隋大业(公元605—618)年间,桥长64.40 m,是现存世界上跨径最大、建造最早的单孔敞肩型石拱桥.你知道怎样确定桥拱圆弧的半径吗?”
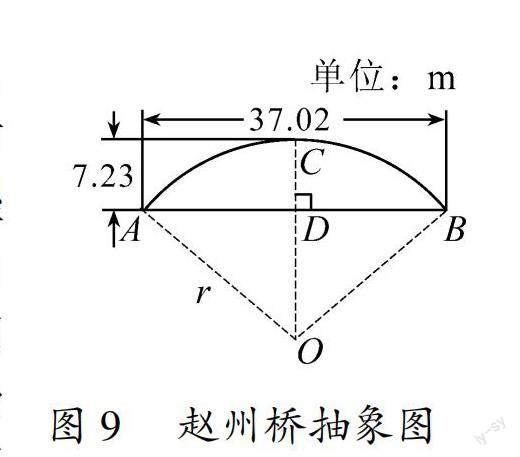
掌握了垂径定理后,解决节前语,例3:已知节前语所示的赵州桥的跨径(桥拱圆弧所对的弦的长)为37.02 m,拱高(桥拱圆弧中点到弦的距离)为7.23 m.求赵州桥的桥拱圆弧的半径(精确到0.01)(图9).
以探索现实情境为需要,解决数学问题,将所学知识巧妙融合于其中,学生既能成功求解,又能在其中感受中国古人的智慧,陶冶爱国情操.由于赵州桥只是圆弧的一小部分,我们利用圆的知识去解决时,可先设所在圆的圆心为O,半径为r(m).因为C为AB的中点,CO为半径,依据垂径定理逆定理可知CO垂直平分AB,由题意,得AB=37.02 m,CD=7.23 m,继而可知AD,用r表示OD.在Rt△OAD中,OA2=AD2+OD2,即r2=18.512+(r-7.23)2,解方程得r≈27.31.解決这一问题的关键,是根据实物画出几何图形,将具体转化成抽象,相信看到抽象图形的你能快速有效结合圆的知识去完成任务.当我们得出桥拱所在圆的半径时,可知赵州桥拱之所以能如此平缓,正是因为它所在圆十分巨大!无独有偶,2013版人教版“义务教育教科书·数学”九年级上册第24章圆的阅读材料中也为同学们介绍了圆周率π的由来[3],随着圆内接正多边形边数的成倍增多,它们的周长p越来越接近圆的周长c.现在的你肯定可以理解为何巨大的圆拱可以近似地看作一段段直边拼接而成了吧!
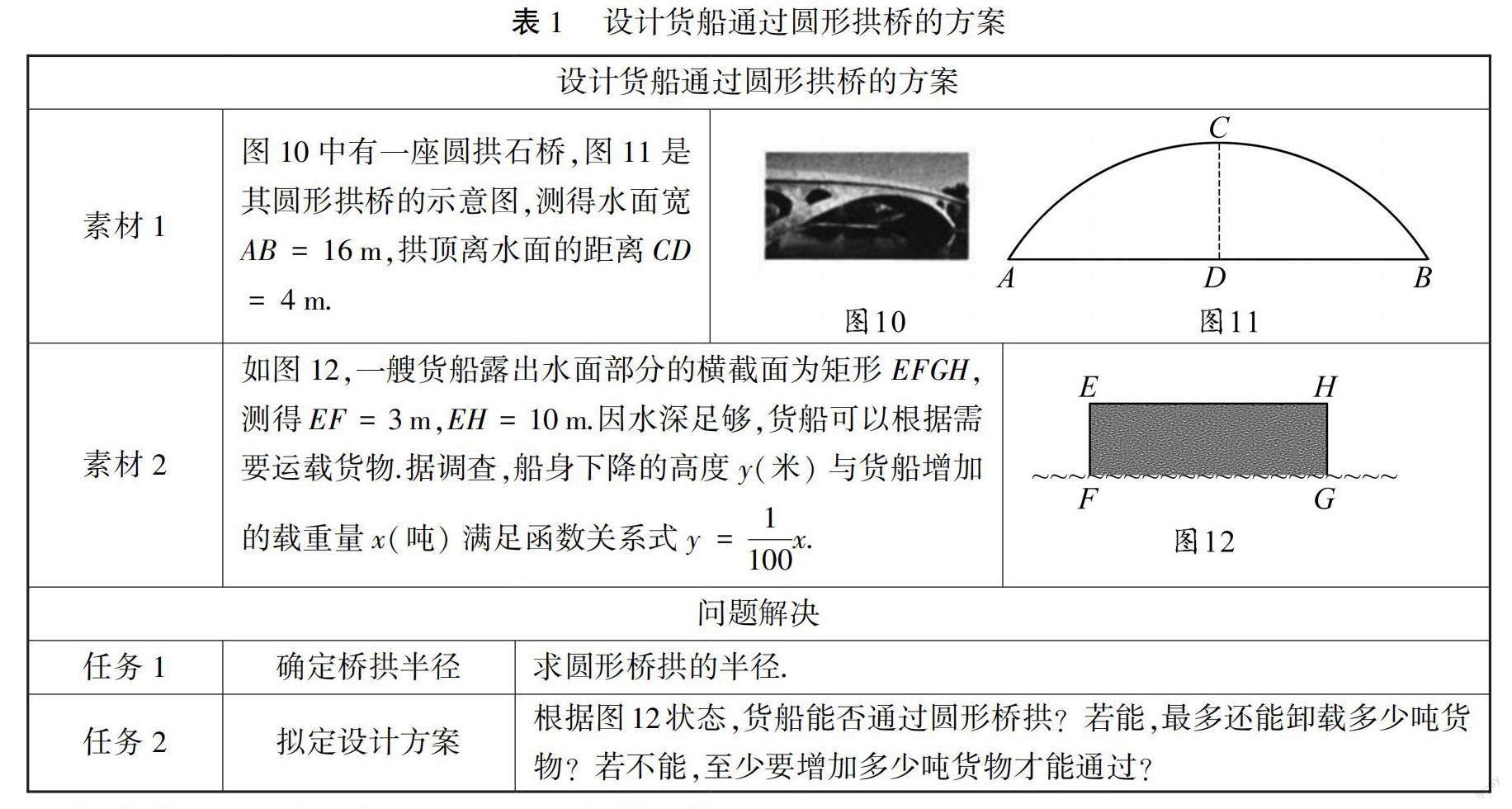
桥拱作为圆的知识教学素材,也能在数学题中找到它的影子,2022年温州九年级期末卷中,需要同学们根据素材解决问题(表1).
相较教材例题,这里增加了两次垂径定理的使用,及一个反比例函数的关系最后转化.(图13)任务1,通过垂径定理,构造Rt△ADO,列式(r-4)2+82=r2,求得半径为10米;任务2,再次利用垂径定理,在Rt△EMO中,勾股列式求解MO,后续便是结合实际情境,分析MD的长度,判断货船能否通过圆形桥拱,再借反比例函数转化求解需要货船增加货物的质量.
利用正多边形与圆的知识,刘徽首创“割圆术的应用也能在初中数学题中找到落脚点.如用圆的内接正多边形逐步逼近圆来近似计算圆的面积(图14),若用圆的内接正八边形的面积S1来近似估计⊙O的面积S,设⊙O的半径为2,求S-S1的值.熟练基本知识的你可以得到每条边(弦)所对的圆心角的度数为45°,并对连半径后分割成的8个正三角形作高求面积和,即可得到结论4π-82.相信敏锐的你也发现了这个结果表明圆内接正八边形与圆的面积实际误差已经很小了,可见古人以直代曲的思想来割圆是蕴含着极大智慧的!
圆形桥拱中有数学,又有文化,更是学生数学学习不可多得的良好素材,当我们结合数学知识去解决现实问题时,一方面需要将情境抽象化探寻现实中的数学魅力,另一方面也需要将抽象数学具象化,感受情境的内涵和其透露的艺术与生活的感染力!
参考文献
[1]张维忠.文化视野中的数学与数学教育[M].北京:人民教育出版社,2005:120-128.
[2]范良火.义务教育教科书·数学(九年级上册)[M].杭州:浙江教育出版社,2013:76-80.
[3]人民教育出版社 课程教材研究所 中学数学课程教材研究开发中心.义务教育教科书·数学(九年级上册)[M].北京:人民教育出版社,2013:109-110.
作者简介 林琪瑜(1993—),女,浙江温州人,中学一级教师;主要从事中学数学教学研究.
张维忠(1964—),男,甘肃天水人,博士,教授;主要从事数学课程与教学研究.
中学数学杂志(初中版)2023年4期
