基于STAR-CCM+的浮标锚泊系统数值研究

程 洪，王晨旭

（1.交通运输部南海航海保障中心广州航标处，广东 广州 510320；2.天津大学海洋科学与技术学院，天津 300072）

浮标锚链对浮标工作效能有较大影响，因锚链断裂造成浮标的丢失、移位等失常事件频频发生[1]。锚链由于受到环境外力及浮标往复运动的施力，关键位置容易发生疲劳磨损致使锚链断裂[2]。因此，计算浮标锚链受力对预估锚链寿命和可靠性具有重要意义。以往研究通常将锚链简化成锚泊线，通过计算锚泊线的静力平衡方程来求取锚链受力[3]，或是通过锚泊线动力微分方程进行求取[4-5]。无论静力还是动力算法，在计算浮标标体在风浪环境中受力时大多采用了经验公式[6]。例如，秦艳丹等[7]用《海港工程设计手册》给出的方法计算波浪力，并根据计算结果设计了锚链长度。聂孟喜等[8]选择莫里森经验公式计算波浪载荷，并用经验公式计算了风载荷。JIN Y 等[9]建立了计算浮标锚链的水动力特性数值模型，在考察环境载荷对锚链影响时，也选用了莫里森公式计算波浪载荷。

经验公式存在计算精度不足的问题，计算流体力学（Computational Fluid Dynamics，CFD）仿真采用更准确的描述波浪的数学方法，得到计算结果的准确度也有提升。PALM J 等[10]比较了4 种计算浮标系泊的方法，第一种是CFD 仿真，采用雷诺平均法；第二、三、四种是不同形式的莫里森公式。研究发现CFD 方法作为高保真的计算方法，可以用来评估水动力参数并依据其计算结果改进参数，而选用莫里森公式会带来力矩失准的问题。另外，浮标与锚链连接处由于存在活动空间，浮标向锚链施力时在连接处会产生力的损失，这是前人研究中较少关注到的问题。如果借助CFD 求解此问题，可以在建立物理模型时引入有针对性的计算方法，将此部分受力损失计入结果。在以往研究中为了简化处理计算，多将浮标锚链简化成单锚泊线[11]，例如SUNDARAVADIVELU R 等[12]做了单点系泊浮标在波浪中的水池实验，测定了不同浪高下锚链受到的拉力。在工程实际中通常是双股马鞍链节挂在浮标底部两侧，通过圆令与短链节相连[13]，这种连接方式也需要考虑，以便接近工程实际状况。

本文基于STAR-CCM+，采用五阶斯托克斯理论建立了3 种海况下的风、浪耦合数值流场，建立了锚链双点连接的浮标模型，并考虑了锚链与标体连接处的受力损失，在这些基础上计算了一种滚塑浮标的锚泊系统受力。

1 数值方法

1.1 控制方程

控制方程为拉普拉斯方程。

式中，鬃表示流体的速度势，应该满足的边界条件如下。

1.2 造波方法

在拉普拉斯方程控制下，基于FENTON J D[14]的研究可构建五阶VOF 波模型，五阶斯托克斯理论生成的波形相比于一阶波形更接近真实。FENTON J D 纠正了SKJELBREIA L 等[15]推导的五阶波表达式的错误，并将SCHWARTZ L W[16]所提出的两个无纲量组成的未知数ak 缩减到只有波数k 一个无量纲的未知数，这样单个非线性方程即可求解，是比较完善的五阶波求解方法。关于k 的表达式如下。

对于本文所研究的包含空气与水的二相流问题，采用欧拉方法进行模拟，界面捕捉为VOF 方法。VOF 方法在流体网格中引入了体积分数a 这一物理量，a 在0 和1 之间取值，当a 为0 或1 时，表示网格中只存在一种流体；当a 为其他值时，表示网格中存在两种流体，所有这些网格就构成了两相流体的交界面，具体到本文，即为自由表面。引入了体积分数之后，流体密度籽和动力黏性系数滋变为如下形式。

式中，q =1 和q =2 时，aq分别为空气相与水相的体积分数，且两者之和为1。体积分数还满足如下输运方程。

在计算时，如果计算区域不设置消波区域，会导致出口处的波浪反射并相互叠加，该处的波面模拟受到严重干扰。随着计算时间的增长，出口处的干扰越来越明显，就会造成波面出现异常，从而导致流场整体特征的改变，最终导致模拟的流场失真，更可能出现计算报错。因此需要在计算域两边边界处设置适当的消波区域，用以消除波浪反射。通常来说，消波区域的长度由波浪长度决定，大约为1.5 倍波长。本文采用Wave Forcing 边界消波，在指定距离内，迫使离散化纳维-斯托克斯方程的解趋向于另一种解，从而使用更小的求解域来减少计算工作量。

1.3 受力计算方法

STAR-CCM+中风阻力由伯努利方程计算而来，波力计算采用KIM J[17]的方法，即通过输运方程添加源项来获得波力。

式中，酌为力系数；籽为流体密度；准为输运方程的当前求解；准*为力求解所接近的值。

浮标锚链的张力由浮标运动产生，在GOODMAN T R 等[18]提出的方法中，将浮标在波浪中运动的频率代入锚泊线受力平衡方程组而求得系泊力。在更多的研究中，为使计算简便，将浮标受力直接传递到锚链上[6-8]。但浮标和锚链在连接处的体-体耦合作用应当予以考虑，由于物体自身重力以及在水中的阻力，致使浮标在向其施力时会产生一定量的损失。因此计算时应减去物体模型之间防止接触的力，即浮标向锚链施力时应减去接触力的法向分量fn，其表达式如下。

式中，k1为弹性系数；k2为阻尼系数；af为面网格面积；df为面形心和相对边界之间的距离；d0为有效范围；为面f 旁的边界面的法向。以上参数可根据具体计算对象的构成材料和几何形状而确定。

在路面施工中会使用到较多的大型机械设备，例如摊铺机、装载车等等，这些大型的机械设备需要在施工现场进行交叉作业，设备管理的难度增大，如果调度出现问题，可能会引发交通事故。

2 模型设置

2.1 模型建立

该浮标标体采用聚乙烯、316L 不锈钢和其他材料复合制造而成，标体各部分采用法兰螺栓连接。标体直径为3.0 m，吃水深度为2.0 m，灯焦面高度为6.043 m（图1）。其各部分重量如表1所示。

图1 滚塑浮标模型

浮标锚链模型在STAR-CCM+中以悬链线方程生成，不需要单独建模，调用悬链线模块并添加至浮标模型上，锚链连接处便可完成锚链模型的设置。

2.2 计算域设置

数值模拟的计算域与网格划分相关情况由图2、图3 给出。计算域长和宽如图2 所示，可确保波浪充分发展并消除壁面影响。因为当水深超过一半波长时，流体的运动可忽略不计，被视为无限水深，所以水深可适当选取，本文中水深为14.5 m。可利用STAR-CCM+的3-CAD-Model 模块建立的浮体全尺寸模型，需要指出的是，虽然在此处未建立防护栏与肘板的模型，但在计算浮体质量、惯性矩及重心位置时是将它们考虑在内的。图2 为计算域的尺寸图，由于采用的是重叠网格法，因此存在背景区域、重叠区域两个区域。边界中的Top Inlet 与Bottom Inlet 均为Velocity Inlet 边界条件。如图3 所示，在波浪发生区和浮标壁面周围加密，网格数量约为500 万，时间步长0.005 s。

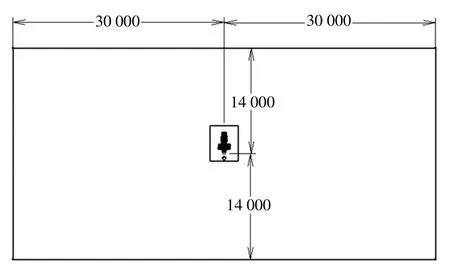
图2 计算域

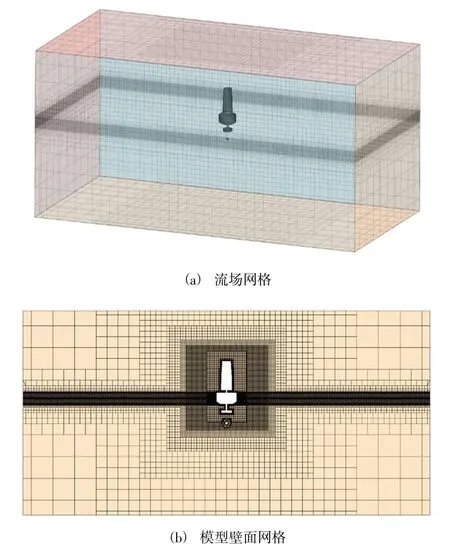
图3 网格划分

2.3 五阶波仿真验证

选择2、3、4 级海况作为计算工况，工况设置如表2 所示。

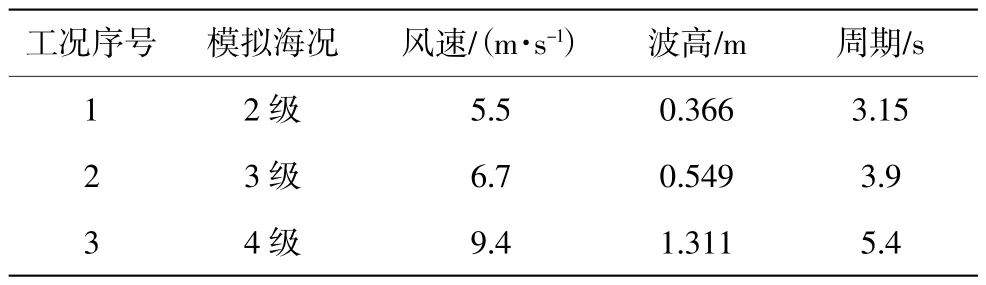
表2 工况设置

依据本文1.2 中的造波方法在3 种工况下模拟斯托克斯五阶波，数值计算结果如图4 所示。在3种工况下至少10 个周期内，波形均保持良好，整个流域长度范围内拥有5 个波形。从波浪曲线来看，完整且准确地表达出了斯托克斯五阶波的波形，这与刘红兵等[19]给出的结果相一致。由本数值水池计算得到的波形结果可以证明数值仿真过程可信，能够为得到准确的计算结果提供保障。

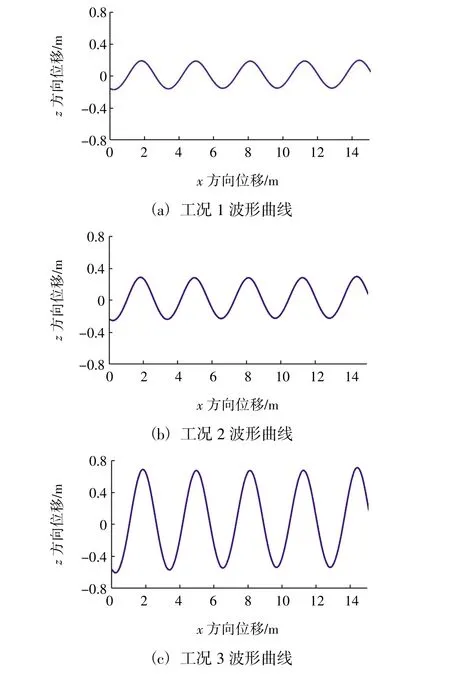
图4 斯托克斯五阶波波形曲线

3 结果分析

3.1 锚链受力分析

如图5 所示，依据式（7）用双股系缆模拟马鞍链节，以圆环模型模拟圆令，单股系缆模拟短链节及半、全链节，锚链重量依据锚链表取锚链直径50 mm 的单位重量为50 kg/m。浮标在风、浪中的阻力和锚链系泊力结果如图6、图7、图8 所示。力的法向指向水面为正，前23 s 为计算不稳定阶段。可以看出双股系缆受力并不是相等的，因为浮标转动会造成一侧锚链受力加大，但双链节所受系泊力之和等于单链节系泊力。随着浮标在规则波中的运动系缆受力在时域上呈振荡分布，在2 级海况时，系缆受力呈小幅波动状态，系缆3 最大受力绝对值为1 782 N。系缆2 为主受力双链节，它的波动频率高于系缆1，且承担了90%以上的受力，因此建议双股马鞍链节应选择与单股链节一样规格的锚链。系缆1 波动频率明显小于系缆2，其最大受力为147 N，处于比较松弛的状态。

图5 仿真计算模型

图7 工况2 时的浮标阻力和系缆张力

图8 工况3 时的浮标阻力和系缆张力

从图6（b）、图7（b）、图8（b）中可以看到系缆2 受力最大值呈小幅降低趋势，系缆1 随着总系泊力的增加开始分担更多的受力。例如4 级海况时系缆1 的最大受力较3 级海况时增加343 N，可以看出系缆3 上增加的受力更多来自系缆1，说明随着风浪作用增强，系缆1 不再是松弛的状态。

因为浮标在规则波中运动，因此从浮标和锚链的最大受力考虑受力损失。从图6、图7 和图8 中系缆最大力和浮标最大阻力对比可以得到在2、3、4 级海况时，浮标阻力损失分别为17.1%、36.6%、55.8%，由此可以看出浮标对锚链的系泊力受风浪力越大，其对锚链的系泊力损失越大。

3.2 浮标升沉运动分析

浮标随波浪上下起伏的同时还受到锚链的牵制，在计算锚链布放长度时需要将升沉造成的锚链拉伸长度考虑在内，留出弹性余量使锚链不至于太过紧绷而导致应力过度集中。因此，考察浮标升沉运动是计算锚泊系统的重要部分。如图9（a）所示，可以看出在2 级海况下，浮标的升沉运动幅度较小。将前15 s 定为计算不稳定时间，去除不稳定时间内的曲线值，浮标的平均升沉幅度为0.08 m。相比平均升沉幅度，计算锚链长度时更应关注最大升沉幅度，2 级海况时计算得出的最大升沉幅度为0.12 m。如图9（b）所示，同样去除前15 s 计算不稳定时间，得到在3 级海况下平均升沉幅度为0.21 m，最大升沉幅度为0.24 m。如图9（c）所示，在4 级海况下浮标升沉幅度有较大程度的增加，前15 s 不计在内，升沉幅度平均值为1.92m，最大值达到2.25 m。

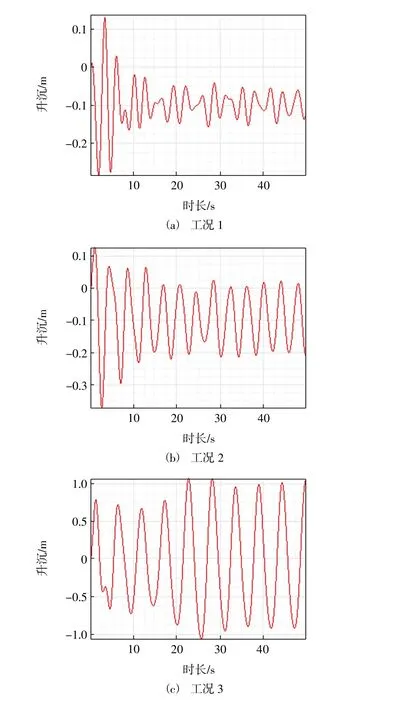
图9 浮标升沉幅度

从工况1 到工况2 浮标升沉幅度变化较小，因为波高的增大幅度所导致力的增大不足以明显地反映在克服浮标重量上。在达到工况3 时浮标的升沉幅度骤升，因为波高增大导致向上的力增大，已达到可以明显抬升浮标的程度。从FENTON J D[14]的斯托克斯五阶理论中可以进一步明确波高增大带来的力的变化。由式（3）可以得到波浪中物体上任一点的受力表达式。

式中，p 为物体表面任一点受到的压力；y*为抬升的流体高度；U 为流体水平方向的速度；c 为波速；V 为流体垂直方向的速度。

在没有设定海流的情况下，U 与c 相等是斯托克斯理论的一个假定，此时V 也是0。而波高的增加不能导致液面过多抬升，从图9 中也可以看出3种工况下y*几乎没有变化。浮标底部受波浪向上的力，可以看出底部表面任一点受到力的变化仅与波高有关，真正决定受力改变的项是（1/2着2+1/4着4）。从工况1 的波高0.366 m 增大到工况2 波高0.549 m时，p 值改变较小，而波高增大到工况3 的1.311 m时，p 值将有较大幅度增加。

浮标升沉运动影响锚链的受力，依据浮标的升沉幅度在计算锚泊系统时应留出相应的弹性余量，并设计好锚链的重量。浮标升沉的计算结果会影响锚链长度和直径的选择，需要仔细进行研究分析。

4 结 论

本文应用STAR-CCM+构建三维风浪耦合场模拟3 种海况，建立了更符合工程实际的双股马鞍链物理模型，计及浮标对锚链施力的损失，通过数值计算研究了浮标锚泊系统，得到如下结论。

（1）由于浮标与锚链之间存在体-体耦合，浮标向锚链施力会在连接处产生一定量的损失，浮标受力增加值大于锚链受力增加值。这种耦合效应随着浮标受力增加而愈加明显，这是计算时应当予以考虑的问题。

（2）双链节其中一股为主受力链节，在2 级海况和3 级海况时承担90%以上受力，因此在设计时马鞍链节应与主链节选择同等规格。随着风浪作用增强，次受力链节分担更多的系泊力。

（3）海况从2 级到3 级时，浮标升沉运动幅度微弱增大，平均升沉幅度增加了0.13 m，最大升沉幅度增加了0.12 m。当达到4 级海况时，升沉幅度有明显增大，平均升沉幅度和最大升沉幅度较3 级海况时分别增加了1.71 m 和2.01 m。因此，在设计浮标锚链时应根据海况不同将升沉幅度考虑在内，留出相应的弹性余量。

本文的锚泊系统研究建立在锚链与标体结合的整体上进行，所得结论可用于浮标锚泊系统的设计。