不同径厚比的海底管道压溃屈曲研究

冯 浩，马 超，王有发，刘 天

（1.中国石油天然气管道工程有限公司，河北 廊坊 065099；2.中国石油集团海洋工程重点实验室，河北 廊坊 065099；3.国家管网建设项目管理分公司，河北 廊坊 065001）

近年来，我国的深海油气资源开发工作快速发展，海洋油气管道的铺设水深记录也在不断刷新。随着工作水深达1 542 m 的陵水17-2 气田铺管作业的顺利实施，我国海底管道行业正式进入1 500 m水深以上的“超深水”作业范围。然而，深水的风险也随之而来，水深每增加100 m，管道外部水压便增加1 MPa，在外部巨大的静水压力作用下，管道存在压溃屈曲的风险，一旦出现泄露，将给海洋环境带来不可估量的危害。管道的壁厚是决定管道承载外部水压能力的主要影响因素，壁厚越大，管道承载外部水压能力越强。由于管道输量明确后，其管径已经固定，因此通常将壁厚指标化为径厚比，作为研究管道承载外部水压能力的主要指标。

国外对海底管道压溃屈曲的问题研究已有逾百年的历史，TIMOSHENKO S P 等[1]提出二维圆环假定，假定管道具有理想的弹塑性，由此研究出了求得屈曲压溃压力的方法。KYIAKIDES S 等[2]提出了一种新的圆环模型，该模型由连续介质构成，采用具有一定局部椭圆度的圆环，该圆环只可沿径向产生变形，用来研究管道屈曲压溃及传播。TAMANO T 等[3]通过对实验数据进行回归分析统计，建立了套管抗压溃的经验公式。YEH M 等[4]考虑了初始几何缺陷、残余应力和初始非弹性各向异性的影响，对径厚比在10耀40 之间的管道进行了实验，提出了计算压溃的通用公式。ASSANELLI A P 等[5]在对比三维有限元模型和二维模型后，发现三维有限元模型的计算精度更好，建议在建模时首选三维模型。MAHMOUD A 等[6]研究了径厚比在15耀40 的双层管道压溃屈曲特性，提出了内管的压溃屈曲公式。RUUD S 等[7]评估了DNV 规范局部屈曲公式对小径厚比管道的适用性，提出随着径厚比的降低，管道的局部屈曲压力将接近屈曲压溃压力。MAHMOUD A 等[8]评估了在管道表面增加制作纹理对压溃屈曲的影响，并给出了该管道的压溃屈曲公式。近年来，国内学者也对海底管道的压溃屈曲问题展开了广泛的研究。HE T 等[9]研究了深海管道的屈曲压溃与椭圆度、径厚比、屈服强度和材料的各向异性的关系。YU J X 等[10]考虑了材料在塑性变形阶段的硬化效应、材料的各向异性，建立了管道压溃压力计算模型。张日曦等[11]研究了压溃屈曲理论公式对于小径厚比管道的适用性。孙震洲[12]从屈曲失效压力标准值的计算理论、经验性系数的取值和复杂载荷的影响等方面开展研究，分析了深水海底管道的屈曲效应。段晶辉[13]研究了在轴力和水压作用下，不同温度和压力的加载路径对海底管道屈曲压溃的影响。李牧之[14]计算了准静态条件下的管道压溃压力及屈曲传播压力。陈达兴等[15]分析了阻尼对管道屈曲的影响，模拟管道屈曲过程并得到临界动力面载荷幅值。冯春健等[16]等以有椭圆度的钢管为研究对象，进行了均匀外压作用下管道结构压溃失效的研究。韩梦雪[17]研究了低周循环载荷下管道屈曲压溃的力学行为，探究了结构损伤失效机理。

综上所述，国内外大多数研究集中在中等径厚比的管道，对深海小径厚比管道和浅海大径厚比管道的压溃屈曲特性分析还不够全面，对工程规范是否完全适用于不同径厚比海底管道的研究也不够深入。目前海底管道领域最常采用DNV 规范计算压溃屈曲临界压力。虽然DNV 规范没有限定海底管道的径厚比，但考虑到DNV 规范将大部分管道屈曲校核公式的适用条件限定在径厚比为15耀45 的区间内，因此，一旦建设单位将DNV 规范作为工程的指导规范，设计人员便往往倾向于将可选用的管道径厚比限定在15耀45 范围内，存在无法充分利用管道材料承载性能、增加工程投资的情况。随着作业水深的增加，壁厚的增大使得管道屈曲行为呈现出了明显的非线性，PALMER A C 等[18]指出，DNV规范公式在对深海小径厚比管道的适用上存在一些问题，龚顺风等[19]也认为DNV 规范方法不适用于深海小径厚比管道，计算结果比实际值偏小。对于深水管道，即使只增加1 mm 的壁厚，也会极大提升管道的铺设难度。因此，有必要进一步核实DNV规范对径厚比在15耀45 之外的深水小径厚比管道及浅水大径厚比管道的适用情况。本文分别采用DNV规范、有限元模拟和深海压力舱试验，研究不同径厚比的海底管道、特别是深海小径厚比管道和浅海大径厚比管道的压溃屈曲特性，并就DNV 规范压溃屈曲计算公式对不同径厚比管道的适用性进行了讨论，提出了适用于不同径厚比海底管道压溃屈曲的设计方法。

1 DNV 压溃屈曲计算方法和局限性

《SubmarinePipelinesSystems》（DNVGL-ST-F101）是目前海底管道工程领域公认最广泛采用的技术规范，采用荷载抗力系数方法进行设计指导[20]。

根据DNV 规范的要求，为防止海底管道发生压溃屈曲，应满足下面的准则。

式中，pc为压溃屈曲临界压力；pel为弹性破裂压力；pp为塑性破裂压力；f0为椭圆度；pe为管道外压；pmin为管道最小内压；D 为管道外径；t 为管道壁厚；酌m 为材料抗力因子；酌SC 为安全等级抗力因子。

从式（1）等号两侧可以看到压溃屈曲临界压力一定小于两个量，分别为弹性压溃压力和塑性压溃压力。考虑到工程中海底管道通常采用API 5L X60、API 5L X65 等级别的钢材，这种材料在塑性阶段具有显著的强化性能，因此以塑性压溃压力作为压溃屈曲临界压力的上限不尽合理，根据DNV规范设计的管道壁厚值较为保守。

对于径厚比在15耀45 范围之外的海底管道压溃屈曲特性，将通过有限元模拟和模型试验进行进一步研究。

2 压溃屈曲模型试验

采用中国科学院力学研究所深海压力舱试验装置进行海底管道压溃屈曲试验。通过全尺寸试验和缩尺比试验研究海底管道压溃屈曲临界压力，验证有限元模拟的正确性，为压溃屈曲设计提供有效的参考和指导。

2.1 试验原理

采用的超大型试验装置是一个可模拟2 500 m水深环境的巨型高压舱体，设计最大水压25.3 MPa。试验装置如图1 所示，压力舱总长12 m，最大内径2 m，可容纳长度不超过10 m，直径不超过1.7 m的试样。

图1 压力舱主体外观

采用盲板法兰密封试验管道两端后，将管道放入如图2 所示的压力舱，利用高压水泵向舱体内不断注水，通过舱内的压力传感器测量压力随时间的变化曲线，如图3 所示。加压一段时间后，试验管道发生局部压溃，此时对应点A，即为试验压溃屈曲临界压力。管道短时间内发生急剧变形后，舱内水压瞬间跌落至B 点，在经历一小段压力波动之后，管道在外压作用下逐步发展成为屈曲扩展，舱内水压恢复到平稳状态。

图2 管道进舱和固定

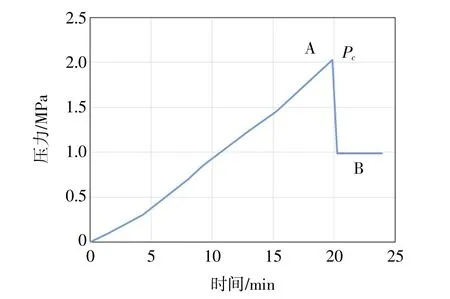
图3 压溃试验的水压-时间曲线

2.2 试验参数

2.2.1 管材参数

试验采用2 种管材，分别为缩尺比试验使用的SS304 不锈钢管和全尺寸试验使用的Q345 碳钢管，材料属性见表1。

表1 试验管道材料属性

2.2.2 管道参数

共设计19 组海底管道屈曲试验，其中缩尺比屈曲试验17 组，全尺寸屈曲试验2 组。具体的试验参数如表2 所示。试验管道编号为A、B、C 的组次分别对应小径厚比、中等径厚比和大径厚比的缩尺比试验管件。F 组次为全尺寸试验组，主要目的在于还原全尺寸海底管道的压溃屈曲特性，且在人为消除管道材料属性对试验结果的影响后，可以在一定程度上作为试验的相似性验证，检验屈曲模型试验问题的尺度效应，为本文研究结论向更大尺寸管道的应用做试验支撑。

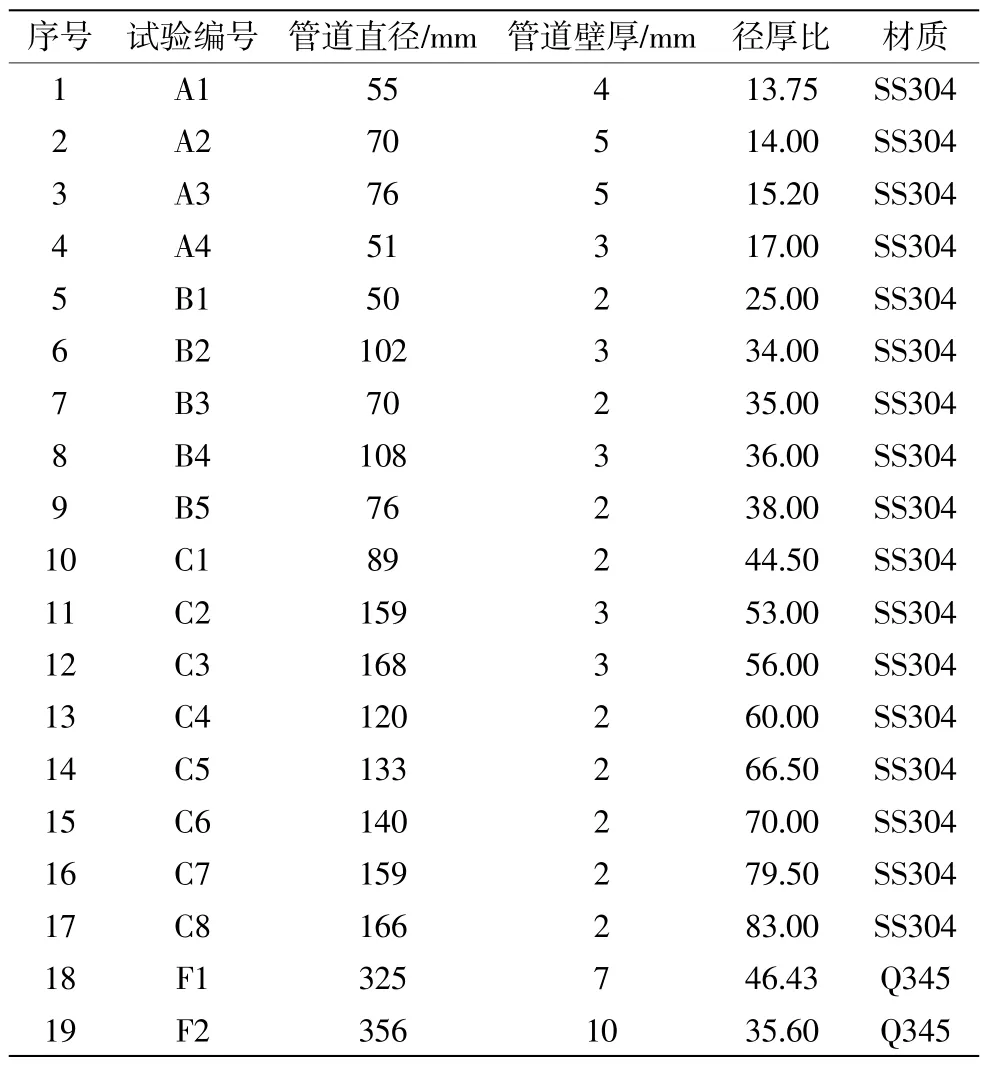
表2 试验管道的参数

3 压溃屈曲有限元分析

海底管道的屈曲问题属于非线性极值型屈曲问题。由于有限元软件ABAQUS 具有强大的非线性分析功能，因此本文采用ABAQUS 进行压溃屈曲有限元分析。在ABAQUS 有限元的计算中，采用忽略加速度的准静态增量迭代法进行求解平衡路径。在前屈曲过程与后屈曲过程的模拟中，使用Newton-Raphson 方法进行迭代求解。采用式（3）Ramberg-Osgood 曲线对管线钢的应力应变本构关系进行拟合。

式中，着为管材应变；滓为管材应力；滓s 为管材屈服强度；E 为管材弹性模量；琢和r 为Ramberg-Osgood 模型参数。

采用静水流体单元加载方法来模拟管道外部静水压力的施加，静水流体单元采用F3D4 单元，代表难压缩或不可压缩的流体，这样就可以将管道外部压力的加载过程转化为流体舱内流体体积的加载过程。当管道发生压溃屈曲时，流体舱的体积也随之变大，进而就可以确定流体作用于管道的压力大小，求得压溃屈曲临界压力。

考虑到管道屈曲的对称性，创建如图4 所示的1/8 管道和流体舱有限元模型。管道单元采用C3D8I 实体单元，流体舱由壳体和端部的壳板组成，壳体半径为管道半径的2 倍，建立在管道外部，端部壳板连接管道外表面和壳体边缘。通过建立不同径厚比、不同材料属性的海底管道模型，模拟海底管道压溃屈曲现象，得到不同条件下的压溃屈曲临界压力。

图4 1/8 管道和流体舱有限元模型

4 结果对比分析

分别采用DNV 规范、有限元模拟和模型试验对表2 的各组模型进行压溃屈曲分析，分析结果见表3。表3 中误差的计算公式如下。

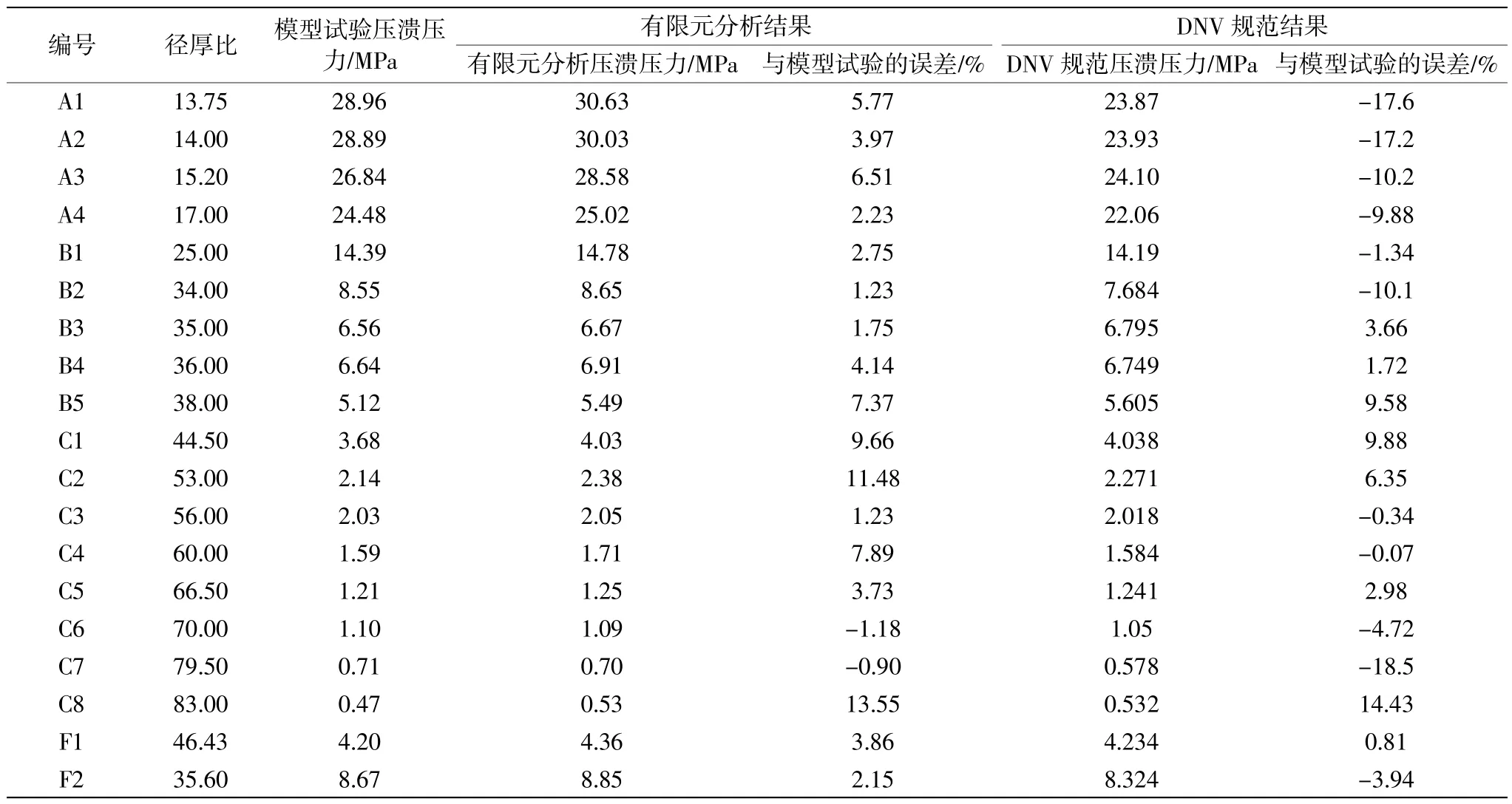
表3 压溃分析结果

经过结果整理，图5 对比展示了不同径厚比管道的分析结果，图6 展示了以模型试验结果为对比基准的分析结果。

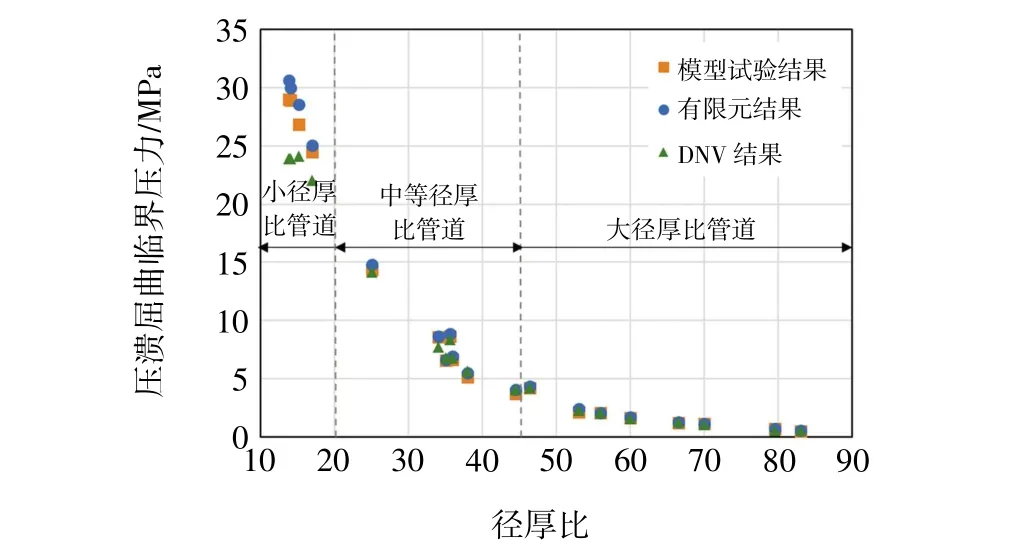
图5 不同径厚比管道的分析结果对比

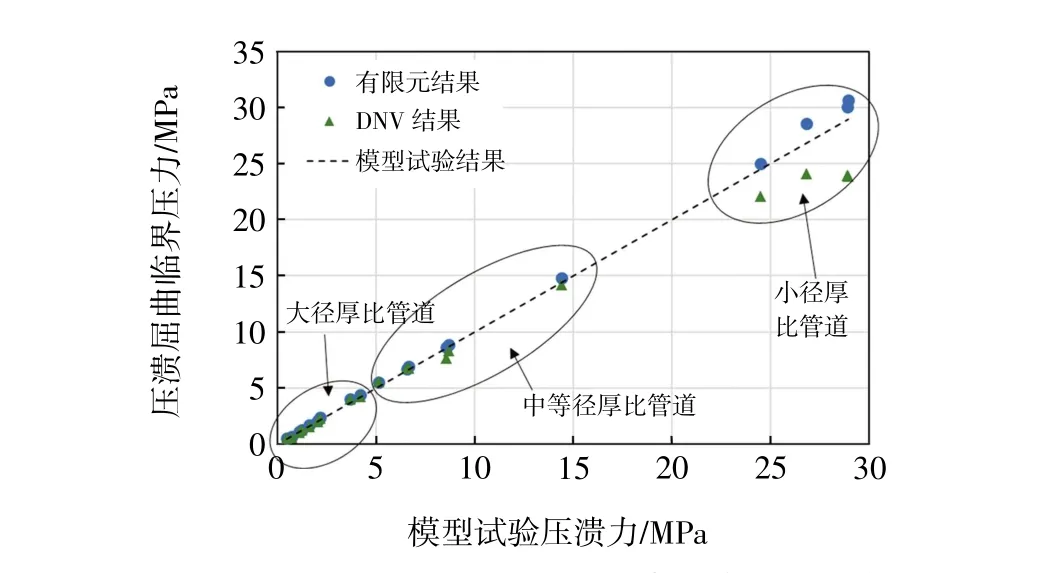
图6 以模型试验结果为对比基准的结果分布

4.1 径厚比对压溃屈曲临界压力的影响

如图5 所示，各种分析方法的结果均表明径厚比对管道的压溃屈曲有着重要影响。管道径厚比与压溃屈曲临界压力呈负相关的关系，管道径厚比越大，压溃屈曲临界压力越小，且这种规律对于小径厚比的管道更加明显，即小径厚比管道的压溃屈曲临界压力对管道径厚比的变化更敏感。因此，对于深海所需要的高水压耐受管道，提高其径厚比是一种可行的方法。

对比不同分析方法的结果，可以看出，有限元模拟结果与试验结果始终保持着较小的误差水平，平均误差为+4.57%。尽管有限元模拟得到的临界压力要普遍大于试验结果，但考虑到在测量试验管件的几何参数时难免会识别不到管件最薄弱的缺陷截面，且无缝钢管在加工制造时也存在壁厚分布不均匀的缺陷，在建立有限元模型时往往无法将这些影响管道压溃屈曲临界压力的因素完美地复现，综合这些因素，有限元模拟计算结果略大于试验结果是可以接受的。

4.2 不同分析方法的结果对比

模型试验可更准确地反映管道的实际情况，因此在图6 中以模型试验结果为对比基准，针对不同径厚比范围的试验组进行了标注。对比有限元模拟结果、DNV 规范计算结果和试验结果，可以得出如下结论。

对于大径厚比管道，有限元模拟和DNV 规范均表现出相当高的预测准确性，与试验结果的误差基本都不超过10%。虽然DNV 规范将大部分管道屈曲校核公式的适用范围限定在径厚比45 以内，但根据表3 的结果，在预测径厚比大于45 甚至达到70 的薄壁管道临界压力时，DNV 规范依旧能与试验结果较好地吻合。当径厚比达到70 以上时，C7 和C8 的结果显示DNV 规范的计算误差较大，表明DNV 规范对超大径厚比管道的适用性较差。

对于中等径厚比管道，有限元模拟、DNV 规范计算结果与试验结果的符合程度均较好，仅有B2的DNV 计算结果误差超过10%。

对于小径厚比管道，对比试验结果，有限元模拟和DNV 规范呈现两极分化的趋势。DNV 规范所得的压溃屈曲临界压力明显低于试验结果，且这种差距会随着管道径厚比的降低而逐渐扩大。相比而言有限元模拟结果依旧要略高于试验结果，但误差处在可接受的范围内（<7%）。DNV 规范推荐的公式较为保守，而有限元模拟结果则与试验值吻合程度较好。

4.3 深海小径厚比管道压溃屈曲设计讨论

根据上述对比结果，DNV 规范计算小径厚比管道的压溃屈曲临界压力较小，即DNV 的设计壁厚明显大于实际所需壁厚。虽然工程中常采用保守设计，但对于深水管道，即使只增加1 mm 的壁厚，也会极大提升管道的铺设难度，增加工程的投资。因此，在进行深海管道的压溃屈曲设计时，从降低工程投资和施工难度的角度，建议采用模型试验结合有限元模拟的方法，计算管道实际可提供的压溃屈曲承载力，设计满足实际需求的管道壁厚。

5 结 论

本文分别采用DNV 规范、有限元模拟和深海压力舱试验，研究了不同径厚比的海底管道、特别是深海小径厚比管道和浅海大径厚比管道的压溃屈曲特性，未来的工作将根据试验结果修正DNV 规范的计算公式，研究结论如下。

（1）管道径厚比与压溃屈曲临界压力呈负相关的关系，管道径厚比越大，压溃屈曲临界压力越小。小径厚比管道的压溃屈曲临界压力对管道径厚比的变化更敏感。

（2）DNV 规范在预测大径厚比与中等径厚比管道（径厚比在20耀70 范围内）的压溃屈曲临界压力时，计算结果与试验和有限元模拟结果符合较好；在预测小径厚比管道（径厚比<20）的压溃屈曲临界压力时，DNV 规范在理论上忽视了管道材料的塑性硬化效应，计算结果较小，并且伴随着径厚比的减小，这种误差不断增大，当径厚比为10 时，误差接近20%。相比而言，有限元模拟结果与试验值吻合程度较好。

（3）在进行深海小径厚比管道的压溃屈曲设计时，从降低工程投资和施工难度的角度，建议采用模型试验结合有限元模拟的方法，计算管道实际可提供的压溃屈曲承载力，设计满足实际需求的管道壁厚。