纤维系缆动刚度特性研究

张火明 洪文渊 王 强 陈阳波

（中国计量学院 计量测试工程学院 杭州310018）

引 言

近年来发展起来的新型绷紧式系泊系统凭借其在深水应用中表现出的诸多优越性而倍受关注。相比传统的悬链线系泊系统，绷紧式的系缆能够提供更大的回复力和更小的平台水平漂移响应；其次，其密度与海水接近，且张力的垂直分量更小，不仅方便了运输和安装，而且也提高平台的有效承载能力；同时，其更小的系泊半径也减小了与其他设施碰撞的危险。在新型绷紧式系泊系统中，系缆一般选用聚酯纤维缆，该材料具有复杂的非线性特性，即粘弹性和粘塑性，致使很难准确把握系泊缆在复杂海洋环境下产生的动力响应。在系缆材料表现出的非线性特性中，其轴向刚度是影响平台最大位移和系缆最大张力的主要因素，所以对合成纤维系缆在循环载荷作用下的动刚度特性进行研究势在必行。

国外已经有较多的组织和机构开展了对新型系泊缆动刚度特性的研究，技术相对成熟。

Del Vecchio［1］测试了纤维丝和直径较小的聚酯纤维缆，发现了平均载荷、载荷振幅和激振周期是影响弹性模量的主要因素，并给出弹性模量和密度的经验公式。基于该公式，Kim［2］采用迭代对动刚度进行了求解，Bosman和Hooker［3］应用子缆和全水深系缆进行实验，发现平均载荷是影响动刚度的主要因素，并提出了弹性模量关系式。

限于国内的海洋工程试验条件，无论在实验模型还是数值模拟方面，国内对于系缆动刚度特性的研究才刚刚起步。

黄维和刘海笑［4］以一艘工作于310 m水深的FPSO为例，对循环载荷作用下纤维系缆的动刚度特性进行了考察，对于悬链式与绷紧式系泊系统进行时域分析，得出了一些有意义的结论。袁梦［5］通过对应力应变为二次非线性关系的锚泊线的拉伸控制方程及任意材料特性的纤维缆的有限元静力和动力控制方程的推导，给出了纤维缆动态刚度的估值方法。林诚鑫［6］基于Schapery热动力学理论和塑性理论提出了一个粘弹性—粘塑性的模型，该模型能够反映合成纤维系缆的应力应变关系和时间变化特性以及在整个加载—卸载过程中的刚度变化。

本文对于循环载荷下纤维系缆的动刚度特性进行了分析研究，改进了系缆动刚度及其张力的计算方法，并编制了求解纤维系缆动刚度的C++程序。该计算方法较之于以往文献［7］的有限元数值分析技术更简洁易懂。并以一座工作于1 500 m水深的Spar平台为例，将理论计算结果与文献数值计算结果进行对比分析。

1 纤维系缆的非线性应力应变行为

由于纤维系缆的非线性特性由很多因素决定，如系缆构造形式、系缆材料、载荷类型等，因此很难准确把握它的非线性行为。在循环载荷作用下纤维系缆应力从0增大到一个最大值，然后再缓慢卸载到0，得到纤维系缆的应力应变滞回曲线。

如图1中曲线所示，在第一次循环载荷后存在一些弹塑性应变，这种现象导致在应力与应变之间存在一个周期性的误差。如果对纤维系缆继续施加相同的循环载荷，会形成很多的滞回环。随着循环载荷次数的增加，就会出现图1所示的弹塑性应变越来越小的现象［8］。

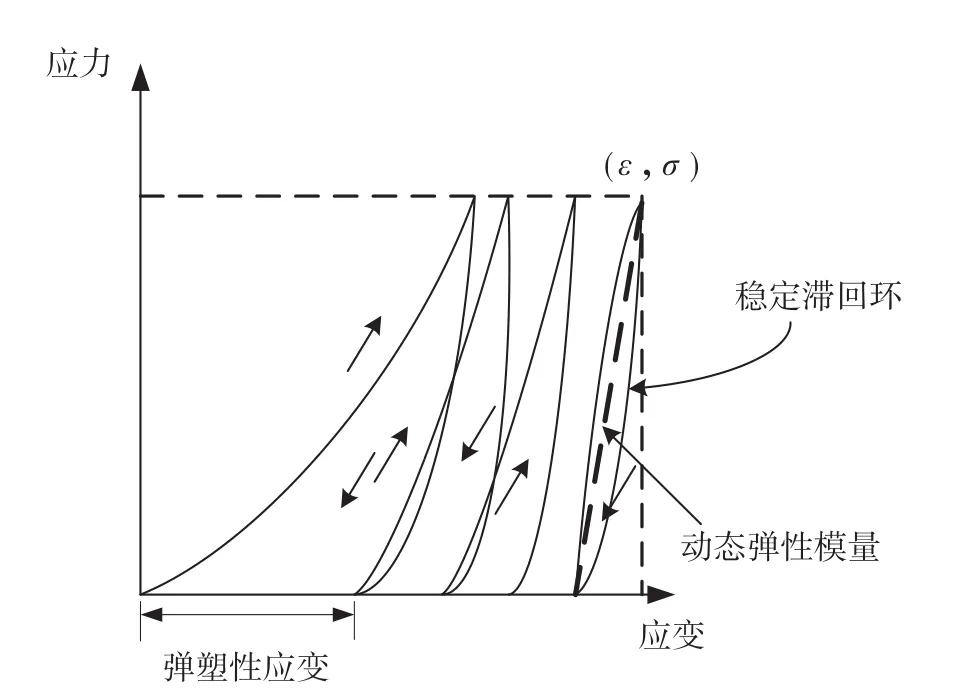
图1 纤维系缆非线性关系图

此外，当载荷次数逐渐增多时，滞回环就会有相互重叠的趋势且逐步趋于稳定。这表明可以建立一个函数来表示应力和应变的关系，该函数值即为系缆的平均弹性模量，它是稳定滞回环的中心线［9］，该值可以呈现纤维系缆对于循环载荷的平均响应。研究表明，系缆弹性模量受循环载荷下系缆的平均张力、张力变化幅值和周期及温度等因素的影响，其中平均张力对其影响较大。

2 弹性模量计算的经验公式

对于纤维系缆的实验研究表明，影响其弹性模量的主要因素是平均载荷、动态载荷及温度。Del Vecchio［1］提出了一个计算纤维系缆在不同外界环境下弹性模量的经验公式：

式中：E为弹性模量，单位为N/tex（1tex=10-6kg/m）；ρ是纤维系缆的密度；Lm为平均张力占最小破断强度的百分比；La为动态张力幅值占最小破断强度的百分比；T为动态载荷的张力变化周期；系数α、β和γ由纤维系缆的构造决定。

公式（1）两边同乘以ρ，得到

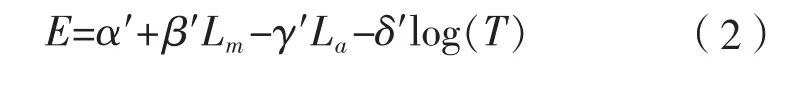
进一步的研究表明，弹性模量的主要影响因素为平均张力和张力变化幅值，而张力变化周期对它的影响非常小，可以忽略［10］。

3 纤维系缆动刚度特性计算

3.1 动刚度求解步骤及流程图

将公式（2）做如下处理［7］：两端同时乘以（MBL为最小破断强度），得到

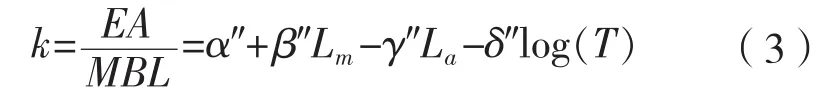
其中k为无量纲的，所以公式（3）为无量纲化动刚度经验公式。

由于前面提到张力变化周期的影响甚微，可以将其忽略不计，故公式（3）可以简化为

动刚度的求解流程如图2所示，求解步骤如下：

（1）求解平均张力。平台由于稳定的风浪流的作用力而产生漂移现象，从而使缆绳发生伸长，产生沿系缆的平均张力，我们在此应用静刚度模型计算平均张力，从而得到Lm，静刚度模型的表达式如式（5）。如果平台在平衡位置附近做简谐运动，那么系缆的平均张力等于预张力。

式中：k0为制造商提供的一个定值，它的大小和缆绳特征有关。

图2 动刚度的求解流程图

（2）迭代求解纤维系缆的动刚度。利用静刚度模型不仅可以求解系缆平均张力，同时也可以求解La。值得注意的是，在此用静刚度模型求解得到的La的值和真实动刚度下计算得到的La的值相差较大。在此我们可以用迭代求解的方法，即将Lm和La代入到（4）式中求得动刚度k，然后利用k再求得新的Lm和La，反复迭代，直到连续两次求出的k的差小于迭代容差时，计算停止，此时k的值即为要求的动刚度值。

基于以上理论开发了求解单根纤维缆动刚度的C++程序，并选取了一个工程实例来验证程序的可靠性。

3.2 系泊系统介绍

以一座工作于1 500 m水深的Spar平台为例，其各项参数如下页表1所示；系泊系统为绷紧式结构，如下页图3所示。

系统由3组聚酯纤维缆组成，3组系缆均匀布置，间隔均为120°，每组3根系缆间隔均为5°。在此假设平台在平衡位置附近做简谐振动，系缆上端点的位移随时间变化曲线为一正弦函数，如图4所示，求解各纤维缆动刚度及张力。

表1 平台各项已知参数

3.3 单根纤维缆动刚度及张力理论计算方法

图4 系缆上端点水平位移变化曲线

为计算方便，首先选取5号系缆为研究对象，如图5所示，假设平台沿x方向运动，系缆上端点随平台主体发生位移，位移随时间的变化历程为正弦函数即x(t)=x0sin(2πt/T)，在此位移幅值x0取为5 m，周期T为10 s，作为工况1。

图5 系缆上端点运动示图

本例中由于平台在平衡位置处作简谐振动故系缆平均张力等于预张力。单根纤维缆动刚度详细求解步骤为：

（1）初始化，令迭代次数n=0、kn=k0。

（2）由静刚度模型计算预张力下系缆的水平跨距。在预张力下纤维系缆伸长后的长度为：L=L0［1+F0/（kn×MBL）］；水平跨距为式中：L0为系缆初始长度，F0为初始预张力，kn为系缆刚度值。

（5）将La和Lm代入式（4），求得一个新的刚度值kn+1。

由于系缆密度与海水接近，所以不考虑纤维缆重力、流体作用力及平台浮体的浮力，根据上述动刚度求解理论计算了纤维缆的动刚度，如图6所示。将计算结果与文献7中有限元数值计算结果进行了对比，吻合较好。

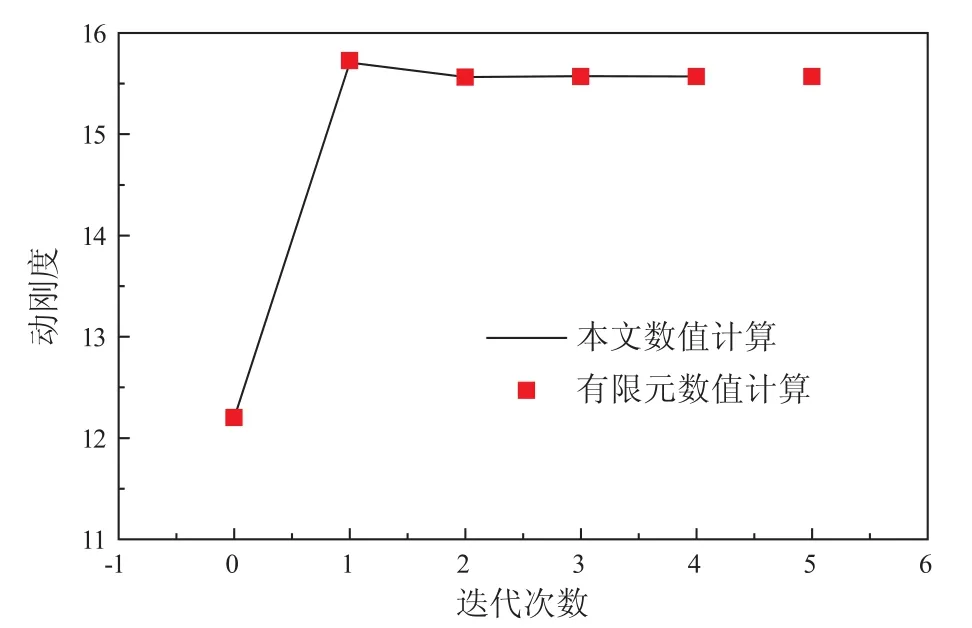
图6 缆5动刚度值

绷紧式系泊系统恢复力是由系缆伸长所产生的张力来提供的。根据纤维系缆收敛的动刚度值k，利用该刚度值的静刚度模型可以计算出一个周期内其张力在每一时刻t对应的位移点处的值，计算步骤如下：

（1）计算纤维系缆在预张力下伸长后的长度：L=L0［1+F0/（k×MBL）］，水平跨距为

（2）计算一个周期内每一时刻的水平位移x(t)=x0sin(2πt/T)。

（3）计算系缆在该时刻的伸长长度：

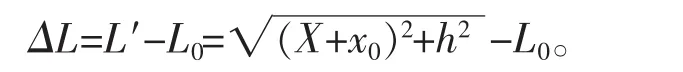
如图7所示，并将计算结果与文献数值计算结果进行了对比。

本文的目的是研究单根纤维系缆上端点在水平面内移动时其动刚度及张力变化情况，因此，为了计算方便，在平台沿x轴运动时，选取缆5作为研究对象。其他系缆的求解方法几乎完全类似，不同之处仅在于计算系缆伸长时，需考虑它与x轴正方向夹角。

图7 缆5张力变化曲线

由以上动刚度及张力求解理论不难看出，其关键技术是求解系缆上端点在位移幅值处或某位移点处系缆伸长长度 。不过应注意的是，此伸长长度是相对于原系缆长度L0而言。

以2号缆为例，某位移点处系缆伸长的长度

计算方法如下（参见图8）：o为锚系点，系缆上端点由a沿x轴正方向运动到b点，求b点处系缆长度变化 。其中，oa为预张力下初始水平投影（水平跨距），L0为系缆初始长度，α为系缆在海底平面的投影与x轴夹角，为系缆上端点沿x轴方向位移。

图8 缆2上端点运动俯视图

计算过程如下：

（2）由余弦定理可求出系缆上端点移动到b点时的水平跨距：

（4）求得b点系缆长度变化从而可以迭代求解动刚度及该刚度值下的张力。计算结果如图9和图10所示。

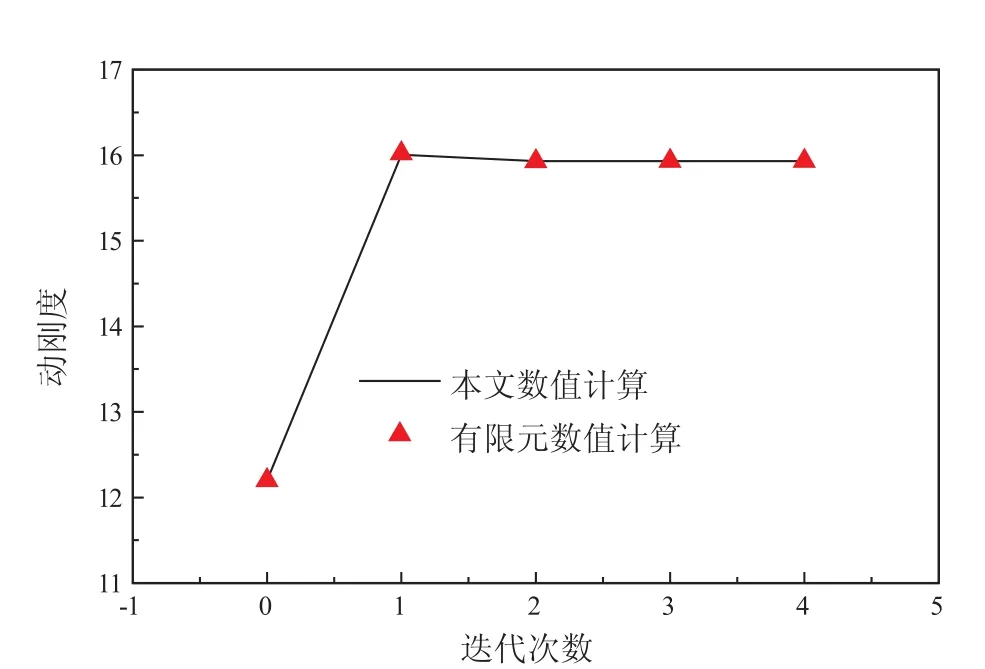
图9 缆2动刚度

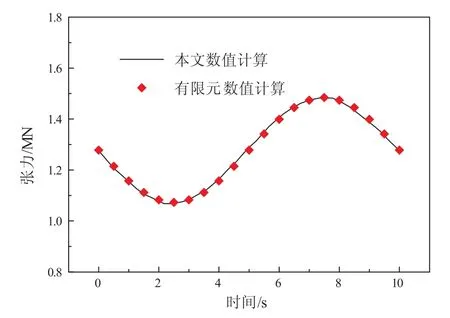
图10 缆2张力变化曲线

对于系泊系统中其他系缆的求解过程与缆2求解过程相同，只是系缆与x轴夹角不同而已。由系泊系统平面布置图（图3）可知，以x轴为对称轴，缆1和缆9对称、缆2和缆8对称、缆3和缆7对称，缆4和缆6对称。由于平台沿x轴发生位移，因此相互对称的两根系缆具有相同的张力及动刚度。

通过将缆5和缆2的动刚度及张力求解结果与文献7的数值计算结果对比，说明本文所改进的理论计算方法是可靠的，故可以用此方法计算系泊系统其他系缆动刚度及张力，计算结果如图11和图12所示。

图11 工况1各系缆动刚度迭代过程曲线

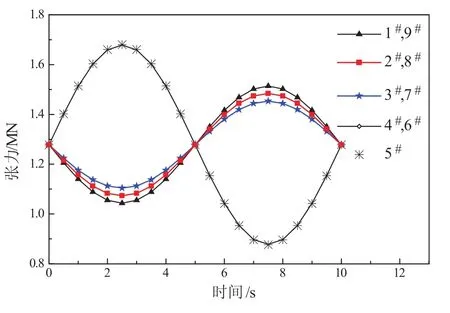
图12 工况1各系缆张力变化曲线

从图12可以看出，由于本工况下平台运动幅值较小，各系缆动刚度迭代过程较为平稳，且很快收敛。各系缆收敛的刚度值下的张力变化较小，且系缆均未出现松弛。当平台主体沿x轴发生位移时，缆5和缆4、6两组系缆与其他三组系缆张力变化趋势相反，且由于此两组系缆收敛的动刚度较小，当发生相同位移时其张力变化幅度较其他三组系缆大。由于缆5和缆4、6夹角较小，所以其刚度值及张力变化非常接近。其他三组系缆刚度值及张力变化也较为接近。

当平台运动幅值x0为50 m、周期T为200 s时，工况2各系缆动刚度值及张力如图13和图14所示。

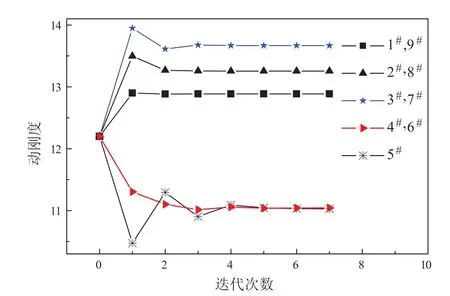
图13 工况2各系缆动刚度迭代过程曲线

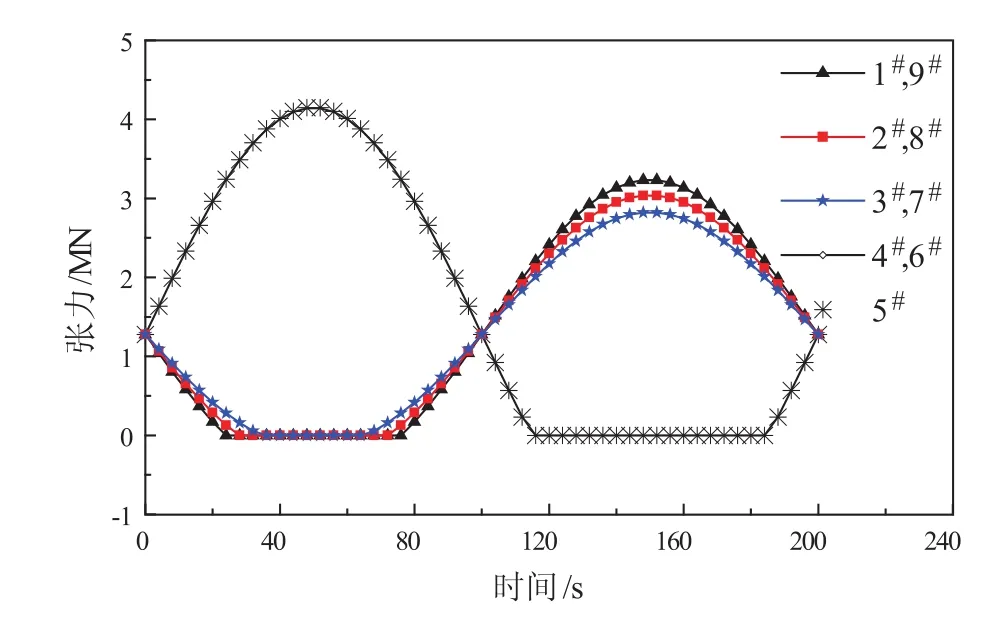
图14 工况2各系缆张力变化曲线

由上述图中可看出，当平台的运动幅值较大时，各系缆动刚度迭代起伏较大，且各系缆最终动刚度值相差较大，系缆会出现松弛的现象。在松弛状况下，其轴向张力为零，且此时系缆张力变化较大，因此张力幅值变化较大，即式（4）中的La较大。由此便知系缆的轴向刚度变小，系泊系统的系泊能力减弱。

4 结 论

本文考虑循环载荷下纤维系缆的动刚度值受平均载荷、载荷幅值及载荷周期的影响，改进了求解新型纤维缆动刚度特性的理论计算方法，此方法简单直观、容易理解。文中还详细介绍了动刚度及张力的求解步骤，将其计算结果与有限元数值计算结果进行了对比分析，发现两者吻合度较高，验证了该理论计算方法的有效性和可靠性。

本文的研究工作可以在一定程度上把握纤维系缆的非线性特性，从而了解绷紧式系泊系统在循环载荷作用下的动力响应。下一步的研究工作将考虑聚酯纤维除动刚度特性以外的其他动力特性，如蠕变、应力松弛等。

［1］ DEL VECCHIO，MENICONI L C.Light Weight Materials for Deep Water Moorings ［D］.Reading：University of Reading，1992.

［2］ KIM M S.Dynamic simulation of polyester mooring lines［D］.Houston：Texas A&M University，2004.

［3］ BOSMAN R L M，HOOKER J.The elastic modulus characteristics of polyester mooring ropes［A］.In：Offshore Technology Conference［C］.Houston，1999.40-44.

［4］ 黄维，刘海笑.新型深水系泊系统非线性循环动力分析［J］.海洋工程，2010，28（2）：22-28.

［5］ 袁梦.深海浮式结构物系泊系统的非线性时域分析［D］.上海：上海交通大学，2011.

［6］ 林诚鑫.深水系缆的动刚度特性研究及系泊分析［D］.天津：天津大学，2012.

［7］ 刘海笑，黄泽伟.新型深海系泊系统及数值分析技术［J］.海洋技术，2007，26（2）：6-10.

［8］ 潘斌，高捷，陈小红，等.浮标系泊系统静力计算［J］.重庆交通学院学报，1997，16(1)：68-73.

［9］ KENNETH R B.Dynamic Modeling of Nylon and Polyester Double Braid Line ［J］.Oceans Engieering and the Environment，1985，17 ：1344-1353.

［10］ FERNANDES A C，DEL V，CASTRO G A V.Mechanical properties of polyester mooring cables ［J］.International Journal of offshore and polar Engineering，1998，9（3）：248-254.