有效运用画图教学解题

蔡园园

一、问题的提出

不少学生解决问题的能力不强，探其原由，主要有以下几个方面。

（一）看数据凑数

比如三年级一道题：“公园里有 12 只黑天鹅，比白天鹅多6 只，黑天鹅的只数是白天鹅的几倍？”部分学生看到多就加：（12+6）÷6，部分学生把“比白天鹅多6 只”当成“白天鹅6 只”，直接12÷6，这些学生对知识表征的认识不清晰，没有建立良好的认知结构；储存的程序性知识没能达到自动化的程度，造成了解决问题时无从下手，只能看数据“脸色”凑数来列式。

（二）缺乏生活经验

比如四年级一道题：一辆正在高速公路上行驶的汽车速度最有可能是（  ）   A.1千米/秒；B.2千米/分；C.50千米/时；D.800米/时。本题正确答案是B，但调查本班43个学生，有36人选C，有4人选A，只有3人选B。与选C的学生交流，他们认为汽车的速度应该是每小时行几十千米，他们不知道高速公路最高时速与最小时速，觉得把2×60=120千米，速度太大了。从中可以看出，部分学生对所学数学知识的实际背景了解不多，缺少必要的生活体验，对来自生活的各种信息不能准确理解。

（三）缺乏系统性的训练

新教材没有把解决问题（应用题）作为一个独立的单元来教学，而是融合于各领域中有机呈现，虽随处可见，但缺乏系统性，一线教师很难把握在什么时候讲授哪类应用题，对于解题的一些方法、策略，部分教师没有很好或不知道如何系统渗透和讲授。另外在每类教学中又有各自的教学重点，部分教师会厚此薄彼，很难把握应用题练习的力度。这样下来，学生碰到这些问题，就不知道怎么解决，用什么方法、策略去解决。

如何提高学生解决问题的能力呢？小学生思维以形象思维为主。据其年龄特点，让学生自己在纸上涂一涂、画一画，借助线段图或实物图把抽象的数学问题具体化，还原问题的本来面目，能有效帮助学生理清题意和数量关系，拓展学生解决问题的思路，帮助他们找到解决问题的关键，从而提高学生解决问题的能力。

二、画图教学的思考

画图教学，是小学数学教师利用画示意图（低年级为实物图、色条图，高年级为线段图）的方式达到“化复杂为简单，化隐性为显性”的目的，让学生更直观地理解抽象、复杂的数学问题的一种教学方法。

（一）学会画图，激发学习兴趣

兴趣不仅是激发学生积极学习的内在驱动力，同时也是学习最好的老师。画图教学法具有形象、直观的鲜明特点，可以将比较枯燥的数学知识变得生动，让小学生享受学习乐趣，激发学生的学习兴趣。如：“有一队小朋友排队做操，从左边数起小红排第5个，从右边数起小红排第6个，这一队一共有多少个小朋友？”教学时，大部分学生喜欢画实物图（ ⊙⊙⊙⊙◎⊙⊙⊙⊙⊙），并理解小红数了两次，用不同的◎表示。部分学生列出算式：5+6-1=10（人），因为小红多数了一次。当教师把题目改成“有10个小朋友排队做操，从左边数起小红排第5个，从右边数起小红排第几？”结果学生发现还可以用原来的图，这时，他们高兴说：“觉得画图很有意思。”

（二）以图求解，化模糊为清晰

部分学生对于数学问题的接受和理解能力较薄弱，这时，教师可以引导他们借助图形的直观作用进行联想，帮助他们理清那些相对复杂的数学问题，从而化模糊为清晰。如教学单价数量总价问题，上课前，教师发现大部分学生能解决简单的这类问题，但当教师出示：糖：1元/颗，10元能买几颗糖？有很多学生列式：10×1=10（颗），虽然答案是10颗，但本题求数量，应用除法。这时教师提问：是10颗吗？学生：是。教师追问：是用除法吗？学生：……这时，教师让学生画线段图，具体如下：

通过线段图，这些用乘法的学生理解10元表示总价，也就是总数，1元表示单价也就是每份数，求数量就是求10元里面有几个1元，用除法计算。

（三）画图搭桥，变抽象为具体

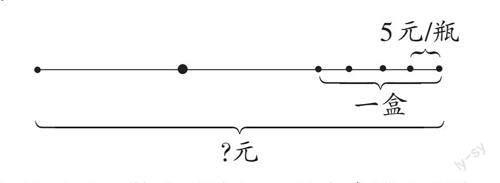
儿童的认知发展规律必须遵循：动作感知—前运算—具体运算— 形式运算，这是不可逆的过程，前后顺序是不变的。而画图教学正是符合这一客观规律的。如“每瓶可乐5元，一盒4瓶，3盒一箱，每箱可乐多少元？”学生对“一盒20元”即表示总数又表示每份数不理解。这时教师引导学生画线段图：哪两个条件是直接相联的，你能画出什么？再根据3盒一箱，你又能画出什么？

在此基礎上，学生理解20元在每瓶可乐5元，一盒4瓶中，表示4瓶的总数，在3盒一箱中，20元表示一盒的单价。在不同的情景下，数量是变化的，这时教师追问：如果5箱装一车，这时线段怎么画呢？数量又怎样表示？学生就很有兴趣。借助一个线段图，就将数学问题中的变化的数量关系直观地显示出来，将抽象的问题具体化，为正确解题创造了条件。

（四）以图促思，变复杂为简单

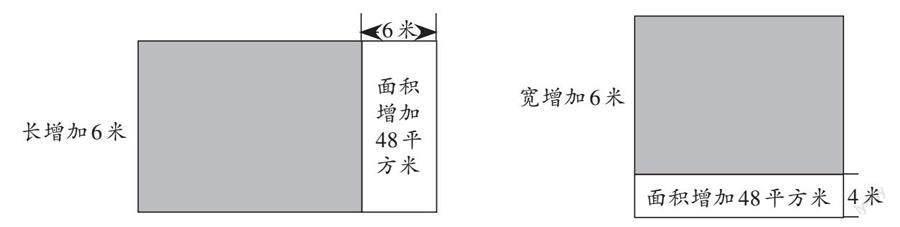
通过图形描述和分析问题可以把抽象复杂的空间几何变得简单形象，帮助学生发现数学问题的本质以预测结果。如：有一块长方形试验田。如果这块试验田的长增加了6米，或者宽增加了4米，面积都比原来增加48平方米。你知道原来试验田的面积是多少平方米吗？很多学生无从下手，因为他们觉得原来长方形的长和宽不知道。这时，教师引导学生画图，具体如下：

发现当长增加6米，面积比原来增加48平方米时，48是后来增加的长方形的面积，6是后来增加的长方形的长，就可以用48÷6=8（米），求出原来长方形的宽。同理用48÷4=12（米）求出原来长方形的长，最后12×8=96（平方米）求出原来试验田的面积是96平方米。

（五）以形助教，理解数学概念

在数学概念教学实践中，将形象的图形和抽象的概念联系起来，将数学概念的内在本质特征以合适的图形表现出来，可以更好地帮助小学生理解和掌握数学概念。如一年级我们就借助一根小棒表示1，一捆小棒表示10，又如在教学60÷3=20，学生能正确计算，但对“整十、整百、整千数除以一位数，可以把被除数看成几个十、几个百、几个千，计算出来的结果就是相应个十、百、千 ”这句话似懂非懂，这时，教师借助计数器，把6个珠子先放在十位，学生根据算式平均分成3份，每份2个珠子，也就是6个十除以3是 2个十，就是20，再依次把这六个珠子分别放在百位、千位，这时学生就发现不管是60÷3=20、600÷3=200，还是6000÷3=2000，都是6个计数单位÷3=2个计数单位，就从本质上理解了算理，而不是停留学生会口算整十、整百数除以一位数。我校教师借助计数器还教学了二进制，通过在计数器拨一拨，画一画，学生们理解了二进制的计数单位是1、2、4、8、16……

三、结语

借图促思不是一朝一夕的，是平时的教学有意识地引导才能形成的。教师要善待每一位学生的绘图“作品”，不管是“力作”还是“劣作”，都要肯定其存在的价值，在充分考虑小学生身心特点的情况下，要善于将内容化繁为简，运用有效的画图教学开展教学活动。