基于变径基圆渐开线涡旋压缩机的几何模型及优化研究

彭 斌, 刘慧鑫, 陶耀辉

(兰州理工大学 机电工程学院,兰州 730050)

涡旋压缩机具有结构简单、噪声低、效率高等优点,广泛应用于制冷、医疗、食品等行业[1].传统由基圆渐开线构成的涡旋压缩机在几何理论、热动力学模型及优化等方面的研究已经趋于成熟[2].而变径基圆涡旋压缩机较高的齿头强度、较低的齿高、较小的涡旋齿质量使得其具有更好的综合性能[3-4].

目前,对变径基圆涡旋压缩机的研究主要集中在型线设计及几何模型推导层面,田亚永[5]利用微分几何共轭曲面理论,证明了变径基圆渐开线作为涡旋型线的可行性;丁佳男等[6]推导了渐开线发生角是否在X轴起始位置的两种变基圆涡旋型线的双圆弧齿头修正几何模型;王吉岱等[7]构建了变基圆涡旋膨胀机的几何模型并推导了各膨胀腔的容积计算公式;唐景春等[8]推导了变径基圆型线齿头双圆弧加直线修正几何模型,研究了修正角度对修正齿轴向投影面积及内压比的影响.

对涡旋压缩机的优化主要集中在几何参数的研究,采用的方法主要为线性加权法、pareto支配法.陈进等[9]首次提出了利用多目标遗传算法优化涡旋型线参数的方法;彭斌等[10]推导了单涡圈双圆弧及双圆弧加直线修正齿头的几何模型,借助多目标遗传算法对各参数进行了优化分析;Peng等[11]利用改进的遗传算法对低压比的双涡圈涡旋压缩机的比功率及型线参数进行了优化选取;刘涛等[12]基于自适应的NSGA-II算法,以轴向力与内容积比为优化目标,对变截面涡旋压缩机性能进行了优化研究.

以上对涡旋压缩机的研究主要集中在等壁厚圆渐开线涡旋类型且关于变径基圆涡旋压缩机几何模型的研究,存在着模型不完善、不精确等问题.同时对变径基圆涡旋压缩机的优化研究考虑的约束较少[13].因此,本文在完善变径基圆涡旋压缩机几何模型的基础上,尝试构建一种考虑约束条件的多目标优化分析模型,为变径基圆涡旋压缩机的优化研究及定量分析提供进一步的理论参考.

1 变径基圆涡旋压缩机的几何模型

1.1 变径基圆涡旋压缩机涡旋齿的几何模型

变径基圆涡旋压缩机涡旋齿结构是由相位差为π的动静涡旋齿构成,其基本几何结构参数如表1所示,根据法向等距原理[14]推导其动涡旋齿型线方程如下.

表1 基本几何结构参数Tab.1 Basic geometric parameters

动涡旋齿外侧型线方程:

(1)

式中:c=δ0/a0.

动涡旋齿内侧型线方程:

(2)

Rob=a0(π-αin-αou)+

(3)

根据表1所示基本几何结构参数构建的齿头修正变径基圆涡旋压缩机在吸气结束时刻的动、静涡旋齿啮合几何模型如图1(a)所示,工作腔从外到内依次为第3压缩腔、第2压缩腔及中心腔, 啮合三维模型如图1(b)所示.

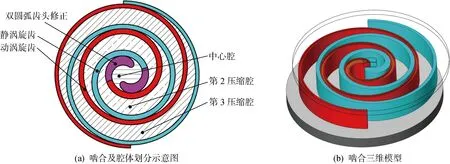
图1 动静涡旋齿几何模型Fig.1 Schematic diagram of geometrical model of orbiting and fixed scroll teeth

由于变径基圆涡旋齿在不同展角处的基圆半径及齿厚都不相同,其齿头修正方法与普通圆渐开线涡旋齿齿头双圆弧修正有一定的差异,文献[3]中给出了其修正原理示意如图2(a)所示.图中:t1,t2,t3为齿头部分3处齿厚的大小;Rin,Rou为修正圆弧及连接圆弧半径;aou为渐开线展角Φ处对应的基圆半径;ρou为外型线的曲率半径;γ,β,λ,d1为修正角度及距离参数.在此基础上,利用面积分块法推导其修正齿面积如图2(b)所示.图中,Sbj为单个完整涡旋齿未修正部分面积.

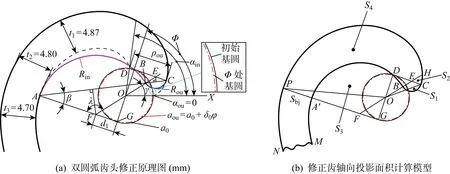
图2 双圆弧齿头修正原理及齿头面积计算模型Fig.2 Modification principle and teeth head area calculation model of double-arc modification

修正齿轴向投影面积为

Sm=S1+S2-S3+S4

(4)

式中:S1为扇形BEC的面积;S3为扇形A′FB的面积;S2为渐开线扇形EHC面积;S4为渐开线扇形OHPO与三角形POF的面积和.

1.2 变径基圆涡旋压缩机3种工作腔容积求解方法比较分析

准确且简便的涡旋压缩机工作腔容积变化规律是其几何模型及热动力学模型建立与求解的关键,目前常用的求解方法有法向等距法[15]、图解法以及格林定理法[16].利用格林定理不难推导封闭压缩工作腔的轴向投影面积为

(5)

式中:xf,in,yf,in为静涡旋齿内侧型线方程.

当φou=φe时有:

(6)

因此,单个吸气腔轴向投影面积计算公式为

As=A(φe)

(7)

压缩腔投影面积随主轴转角θ的变化规律为

A(θ)=A(φe-θ)

(8)

对表1所示涡旋压缩机的基本几何结构参数利用3种求解方法进行求解比较分析,其示意如图3所示.

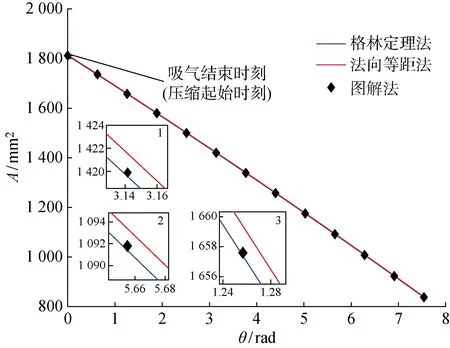
图3 不同容积求解方法计算结果对比Fig.3 Comparison of calculation results of different working chamber volume solving methods

由图3可见,利用3种方法求解的压缩腔轴向投影面积变化规律高度一致.对3个不同转角位置(如图3中1, 2, 3)所示的曲线放大观察,格林定理法与图解法的误差较小而法向等距与其两者的误差相对较大,在这3个位置处格林定理法与图解法的误差分别为 0.036%、0.055%及 0.042 3%,主要原因是作图时的测量误差;法向等距法与图解法的误差分别为0.106%、0.128%及 0.078 4%.两者产生差异的原因是格林定理法的计算过程是直接利用生成变径基圆涡旋齿的型线参数方程进行代入求解,因此,误差相对较小;而法向等距法进行了几何等效处理,在平移组成封闭工作腔的内外型线时会造成微小的面积偏移误差,格林定理法虽然精度较高,但由于组成封闭工作腔的型线类型在不断变化,对于吸气过程及后续压缩过程面积的推导极其抽象复杂[17].相反,法向等距法由于其简单易懂且精度满足要求,广泛应用于变壁厚涡旋压缩机的几何模型快速建立中.

对3组不同几何结构参数的变径基圆涡旋压缩机进行计算分析,研究其吸气结束时刻的单腔轴向投影面积的大小,计算结果如表2所示.表中几何参数1来源于表1,几何参数2和3分别来源于文献[18]和[19].

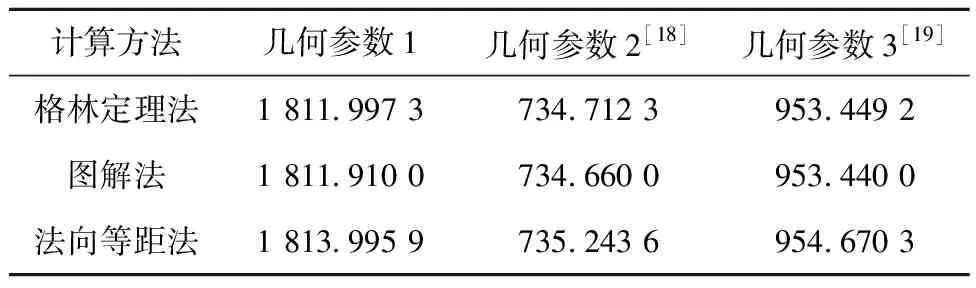
表2 单腔轴向投影面积

从表2可知,3组不同几何结构参数的变径基圆涡旋压缩机的吸气终了轴向投影面积大小满足图3所示的变化规律,再次证明了以上关于几何分析的正确性及通用性.

1.3 完整工作腔容积的变化规律

文献[15]中利用法向等距法给出了变径基圆涡旋压缩机压缩腔及排气腔容积的计算公式,对相应公式进行坐标变换及利用法向等距法推导出吸气腔的容积V0,计算公式如下.

当0≤θ≤2π时,

V0=2HRob{L0+δ0[(φe-π-θ)δ1-

(φe-π)δ1-54.789 1sinθ]}

(9)

式中:H为齿高;L0为基线长,

L0=

(10)

行程容积为

Vs=2HAs=V0(2π)

(11)

式中:V0(2π)为θ=2π时V0的函数值.

理论内压缩比为

(12)

式中:θd为开始排气角;V(θd)为θ=θd时完整工作腔容积V的函数值;k为绝热指数.

由于涡旋压缩机的实际动、静涡旋盘是沿着齿高(轴向)方向进行拉伸生成的,所以工作腔容积及涡旋齿体积的计算为相应几何体的轴向投影面积与齿高的乘积,为了使得计算量减小,令H取值为 1 mm,但不影响变径基圆涡旋压缩机工作腔容积及相应几何模型变化规律的趋势及精确程度.利用MATLAB数值计算软件对表1所示参数的变径基圆涡旋压缩机进行编程计算,得到其从吸气开始到排气结束的完整工作腔容积V变化规律如图4所示.

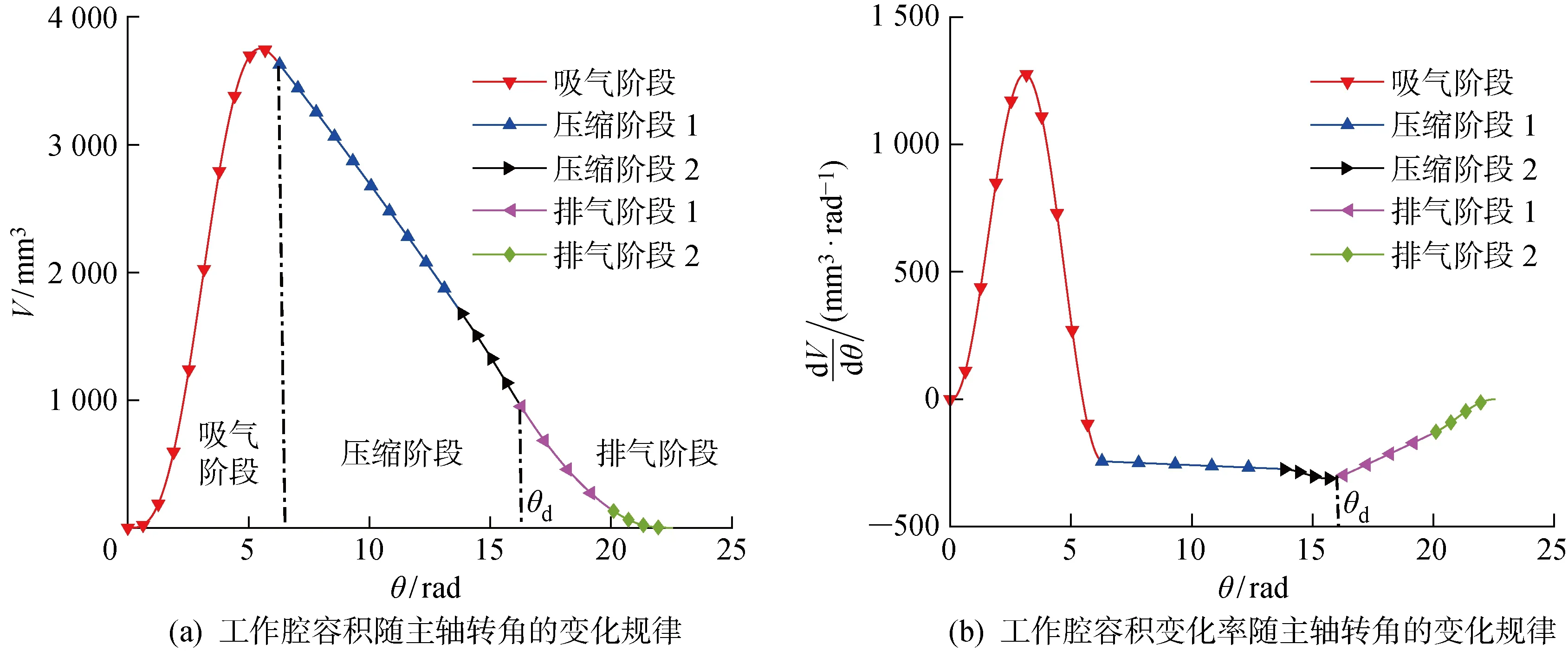
图4 工作腔容积及其变化率变化规律Fig.4 Evolution and derivative of working chamber volume with orbiting angle

图4(a)所示为变径基圆涡旋压缩机完整工作腔容积随主轴转角的变化规律.同其他类型涡旋压缩机一致,在吸气阶段,工作腔容积逐渐增大至峰值然后小幅度的减小直到吸气腔完全闭合,随着压缩阶段的逐渐进行,工作腔容积持续减小直到动静涡旋齿达到最终啮合点即主轴转角为θd时,第2压缩腔与中心腔相连通进入排气阶段,持续到排气腔容积减小为0,排气过程结束.图4(b)所示为工作腔容积的变化率随着主轴转角的变化规律.由图可知,各个阶段工作腔容积的变化速率存在明显差异,吸气阶段,工作腔容积先增加较快,当dV/dθ=0时,吸气腔容积达到最大,随后,dV/dθ<0,工作腔容积逐渐减小一直到排气过程结束.

1.4 齿面积利用率计算模型

由于变径基圆涡旋压缩机的涡旋齿壁厚逐渐变化,属于渐变壁厚涡旋类型,且涡旋齿的面积利用率能够衡量其材料的使用率[20-21],同时也能间接反映工作腔轴向投影面积的大小及汽车空调用涡旋压缩机轻量化的要求,齿面积利用率越小,耗材越少,质量越小.定义齿面积利用率ζ为动静涡旋齿的齿面积和占两者啮合所需最小盘面积的大小,计算示意如图5所示.

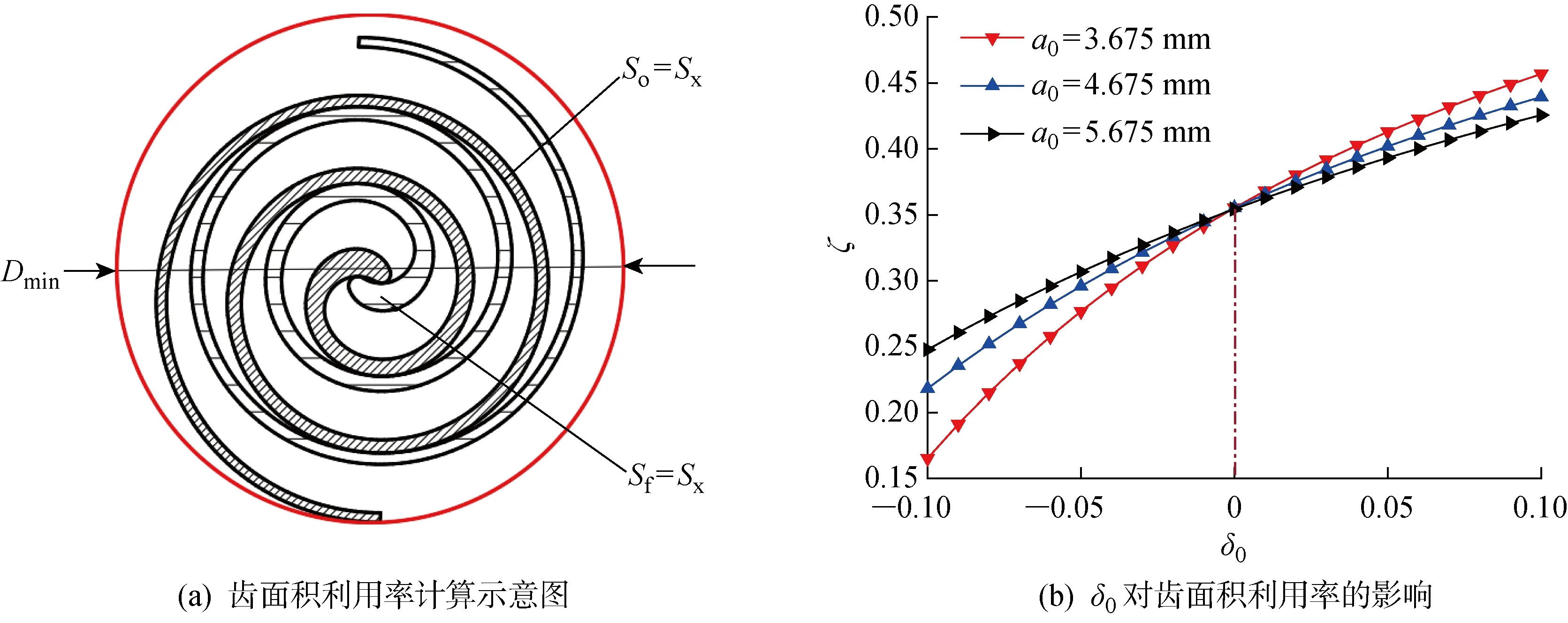
图5 齿面积利用率计算模型Fig.5 Calculation model of area utilization rate

动、静涡旋齿啮合所需最小盘径[3]:

(13)

动、静涡旋齿面积:

So=Sf=Sx

(14)

Sx=Sbj+Sm

(15)

式中:Sm为齿头采用双圆弧修正的修正齿轴向投影面积.

因此,齿面积利用率为

不同初始基圆半径a0对应的齿面积利用率随基圆半径变化系数δ0的变化如图5(b)所示.从图中可知,随着δ0的增大,齿面积利用率均呈非线性的增大趋势,且增大速率越来越慢.不同基圆半径对应的变化规律曲线汇聚于δ0=0点,δ0<0时,ζ与a0成正比;δ0>0时,ζ与a0成反比.同理,随着αin的增大,ζ也相应增大.因此,合理地选择型线参数对齿面积利用率指标有着重要影响.

2 型线参数对齿面积利用率及行程容积的影响

为了研究各型线参数对变径基圆涡旋压缩机几何性能的影响程度大小,为后续的优化分析确定最佳的决策变量,定义行程容积与齿面积利用率的灵敏度模型为

(16)

(17)

式中:Xi=[x1x2x3x4x5x6]T=[a0δ0αinΦφeH]T.

行程容积及齿面积利用率的灵敏度模型如图6所示,从图6(a)可知,a0,δ0,φe,H与行程容积之间为正比关系,αin与其为反比关系,修正展角Φ对其几乎没有影响;从图6(b)可知,a0,δ0,αin与齿面积利用率之间为正比关系,而Φ,φe,H对其几乎不产生影响,δ0,αin对两种几何性能的影响远大于其他参数,且基圆半径变化系数的影响最大.

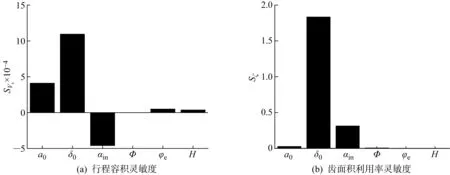
图6 灵敏度分析模型Fig.6 Model of sensitivity analysis

3 多目标优化分析模型的建立与求解

基于建立的变径基圆涡旋压缩机几何模型,对某款汽车空调用变基圆半径渐开线涡旋压缩机[18]几何结构参数及性能进行优化分析,比较不同优化算法求解性能指标的差异.

3.1 目标函数及决策变量的确定

从上述分析知,δ0,αin对行程容积及齿面积利用率的影响尤其显著,且Vs与ζ之间不能同时取得最优,存在明显的冲突关系.因此,选取Vs与ζ为优化目标,δ0,αin为优化决策变量.

3.2 约束条件的确定

(1) 变径基圆涡旋压缩机常用于汽车空调等领域[11].因此,动静涡旋齿的最小啮合盘径定为

80 mm≤Dmin≤150 mm

(18)

(2) 采用法向等距法生成涡旋齿,回转半径大小会影响齿厚大小及内外型线位置.因此,将其定为

a0≤Rob≤2a0

(19)

(3) 为了使得优化分析有意义,须保证优化分析之后的内压缩比不小于优化前的内压缩比.因此,将其定为

ε0≥ε

(20)

(4) 考虑到变径基圆涡旋压缩机在φe处涡旋齿的强度及刚度,将该处齿厚t(φe)定为

1 mm≤t(φe)=[(xm,in(φe-π)-

xm,ou(φe))2+(ym,in(φe-π)-

ym,ou(φe))2]1/2≤3 mm

(21)

(5) 为了使得涡旋压缩机的壁厚变化规律适应工质在工作腔内压力、温度向中心腔靠近逐渐增大的变化规律,将基圆半径变化系数定为

-1≤δ0≤0

(22)

3.3 求解结果及比较分析

多目标优化算法与传统的线性加权法相比,能够把可供决策者选取的多组解以非劣解集的形式可视化,更具优势.多目标遗传算法(NSGA-II)及多目标粒子群(MOPSO)算法是在传统遗传算法及粒子群算法的基础上,加入了非支配排序算子,超体积(HV)、反世代距离(IGD)、计算时间(T)能够衡量算法的优劣,HV值越大,IGD值越小,时间越短,算法越优秀.表3所示为以上两种算法求解标准测试函数BT1的相关性能指标对比.从表3可知,在相同种群数量及迭代次数的条件下,NSGA-II在计算时间、HV及IGD指标均优于MOPSO.图7所示为多目标优化算法NSGA-II及MOPSO求解标准测试函数BT1(f1,f2为其两个目标函数)的结果.由图可见,MOPSO求解[22]获得的pareto前沿均匀性及准确性均差于NSGA-II对应的求解结果.因此,对于测试函数BT1, NSGA-II更具优势.图8(a)所示为只考虑δ0,αin上下边界约束条件的求解结果,由图可知,对于较少的决策变量,MOPSO与NSGA-II能解得差异极小的非劣解集,但MOPSO对应解的分布均匀性弱于NSGA-II, 且计算时间为12.70 s,多于11.11 s.图8(b)为考虑非线性约束条件的求解结果,其计算时间为25.56 s,虽计算效率弱于图8(a)中的结果,但求解的非劣解集更精确,范围更小,决策者选取优秀的解也更容易.从图8(b)中选取一组非劣解及其对应的型线参数与优化前作对比,如表4所示.

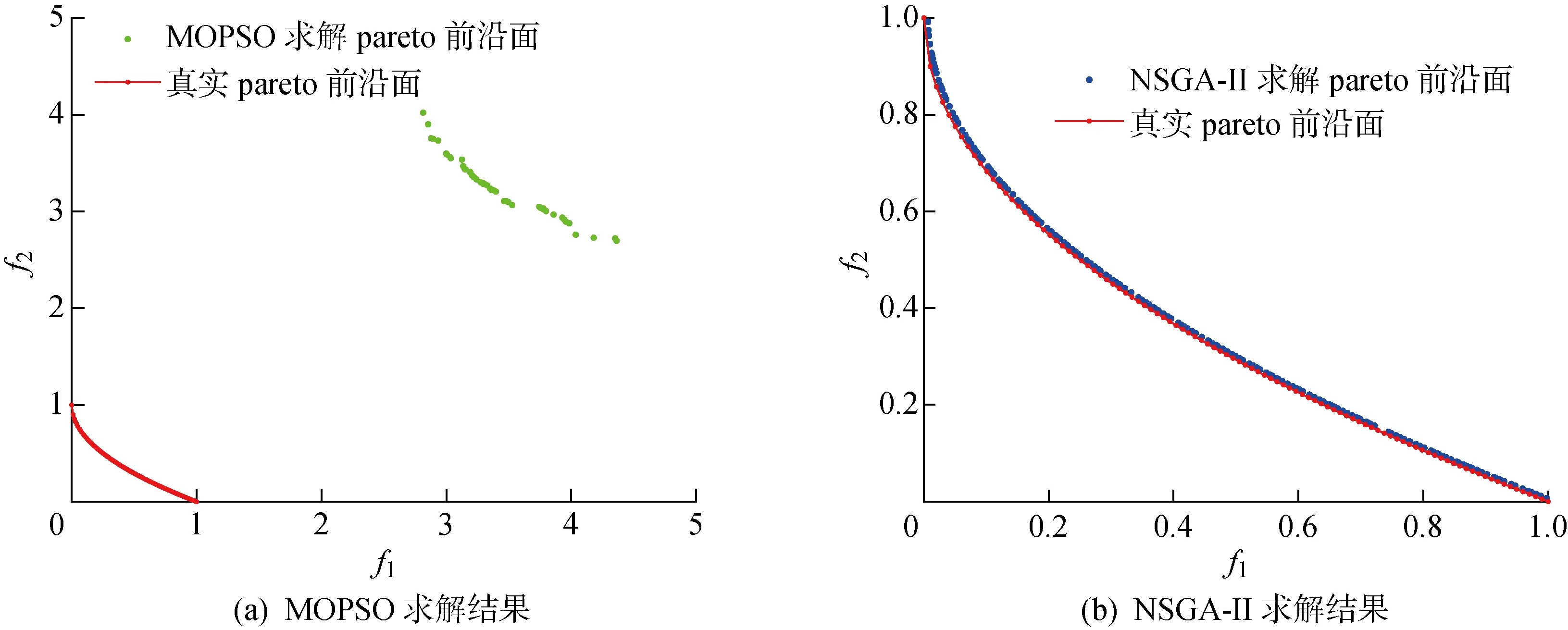
图7 测试函数求解结果Fig.7 Solutions to test function

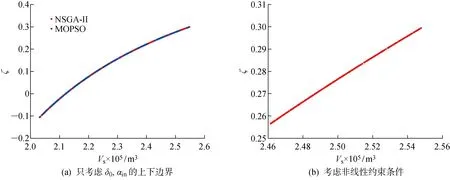
图8 优化分析模型求解结果Fig.8 Solutions to optimization analysis model

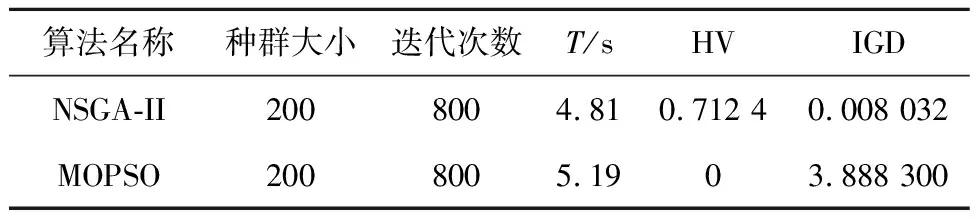
表3 性能指标对比 Tab.3 Comparison of performance indicators

表4 优化型与优化前几何性能对比

由表4可知,优化分析之后的优化型在满足内压比的条件下,较优化前,行程容积增大了6.95%,齿面积利用率下降了4.26%,证明了本优化分析模型的实用性.同时,在本优化分析模型及测试函数上,NSGA-II综合性能均优于MOPSO.

4 结语

完善了变径基圆涡旋压缩机的几何模型,给出了其完整工作过程的容积变化规律,讨论了格林定理法、图解法及法向等距法计算结果的差异性,3种方法的计算结果误差小,均可用于变径基圆涡旋压缩机几何模型的求解,但法向等距法更简单易懂.建立了变径基圆涡旋压缩机齿面积利用率的计算模型,分析了各几何结构参数对行程容积及齿面积利用率的影响程度,发现基圆半径变化系数及内侧型线发生角的影响尤为显著.构建了一种以Vs与ζ为优化目标的多目标优化分析模型,优化分析之后的性能均优于优化前,且优化算法NSGA-II较MOPSO更具优势,该模型能为变径基圆涡旋压缩机的优化研究提供进一步的理论参考.