交变工况下深海装备机械密封端面温升和磨损特性
郑思敏, 滕黎明, 赵文静, 江锦波, 王梦娇, 彭旭东
(浙江工业大学 机械工程学院, 杭州 310023)
海洋是人类发展的四大战略空间(陆、海、空、天)中继陆地之后的第二大空间,随着陆上油气资源的日益枯竭,开发我国南海深海海域的生物资源、能源、水资源和金属资源对提高我国综合竞争力、保障国家安全具有重要意义[1].深海装备是制约我国向深海进军的关键技术瓶颈.深海潜水器是开展深海科学研究的重要支撑,已成为深海装备研究的热点之一.推进器是潜水器上重要的核心部件,潜水器在水下要完成航行或悬停动作都依赖于推进器,而推进器转轴密封的性能对深海潜水器的安全可靠性具有重要影响.因深潜器需在水下停留较长时间且空间有限,故多选用接触式机械密封[2].
接触式机械密封失效主要是由于过热和磨损,故而有必要对接触式机械密封的端面温度和端面间的接触摩擦行为开展深入研究.目前,国内外针对机械密封端面温度的预测方法已有不少.Pascovici等[3]和Blasiak[4]分别建立了热流体动力润滑模型,利用解析法求解了机械密封的端面温度分布.文献[5-7]中利用有限差分法迭代求解能量方程和热传导方程,获得了密封环和液膜的温度分布.Meng等[8]提出一种准三维热力学模型,采用Petrov-Galerkin有限元方法得到了机械密封液膜的压力和温度分布.文献[9-18]中考虑了密封环的热力变形,基于热弹流润滑模型预测了端面温度分布,并研究变形对密封性能的影响.上述研究均围绕稳定工况下密封端面和液膜的温度计算,而在机械密封瞬态温度场方面,文献[19-21]中进行了探索,通过建立瞬态模型对时间项进行离散,研究了典型启动和停车工况下端面温度、泄漏率等密封性能随时间的变化规律.
针对机械密封的磨损特性,研究人员也进行了大量实验工作.Zhao等[22]利用销-盘式摩擦试验机测试了几种密封环材料在干摩擦和水润滑条件下的摩擦磨损性能.文献[23-27]中基于声发射技术,监测了密封端面的接触状态,利用双高斯分层理论预测了端面的形貌演变.文献[28-30]中研究了压力-线速度(pv)值、石墨化度、表面粗糙度等因素对机械密封摩擦学性能的影响.文献[31-32]中通过扫描电镜和红外光谱分析,探究了机械密封浸渍石墨在腐蚀环境下的磨损机理,并提出了石墨制备工艺的改进措施.
综上所述,目前对接触式机械密封端面温升和磨损特性的研究主要集中于稳定工况下,而对于瞬态工况,尤其是交变工况条件下机械密封端面温升及磨损特性的变化规律还鲜有报道.由于在深潜器的航行过程中,其下潜深度和叶轮的工作状态均会对转轴密封的工作条件造成影响,使得推进器机械密封长期服役在工况波动的环境中.在交变工况作用下,密封端面的摩擦接触状态以及热波动特征尚不明确,使得预测和评估深海涉水装备推进器用机械密封的摩擦性能和使用寿命尤为困难.
因此,利用Workbench平台建立带腔内流体的机械密封环二维轴对称模型,重点探究交变工况下其腔内耦合传热特性及密封环端面温升规律.开展机械密封拟实工况试验研究,探究交变工况对机械密封实际工作的影响,监测密封端面温度变化趋势,研究密封端面磨损特性并加以验证分析,掌握密封环磨合过程中端面温升及磨损特性的变化规律,以期为深海涉水装备推进器用机械密封的设计提供指导,对深海涉水装备密封技术的发展和机械密封使用寿命的延长具有实际价值和现实意义.
1 数值模型
1.1 网格划分与边界条件
深海涉水装备作业时承受巨大的海水压力,海水深度每增加 100 m,压力增加可达 1 MPa.深海推进器用机械密封常设计压力补偿器,其可根据海水深度自动调整补偿压力,用以减小海水压力变化对动力装置的影响,使机械密封内外侧压差小于 1.5 MPa[33-34].根据某型号深海推进器的结构参数及实际运行工况[35],本文设计的机械密封腔内耦合传热的二维轴对称有限元计算模型及网格划分如图1所示,图中R为半径.采用Workbench自带Mesh单元对模型进行网格划分,对密封环外周及动、静环接触端面进行局部网格加密.S1~S15为各点位边界,密封腔入口速度设为0.2 m/s,出口压力为 400 kPa;入口温度设为 26 ℃,密封腔内壁温度与入口温度相同.采用重整化群(RNG)κ-ε模型进行瞬态计算,动环为浮动环,动静环之间设置接触对,将动环端面WR设为接触面,静环端面WS设为目标面,密封端面摩擦因数设为0.1,产热方程通过用户自定义标量函数(UDF)程序加载到接触面处.动环材料为浸呋喃树脂碳石墨(M106K),静环材料为碳化硅(SSiC),表1为机械密封模型物性参数;表2为尺寸参数,其中rb为动环边界S2半径长度;表3为清水介质26 ℃时的性能参数.为简化计算,在计算过程中作如下基本假设.
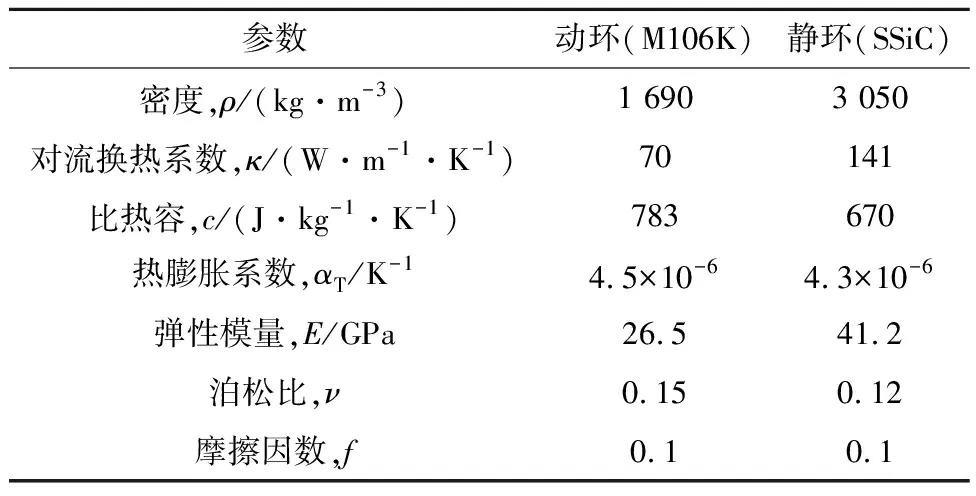
表1 密封环材料物性参数Tab.1 Material properties of seal ring

表2 密封环尺寸参数Tab.2 Dimensional parameters of seal ring
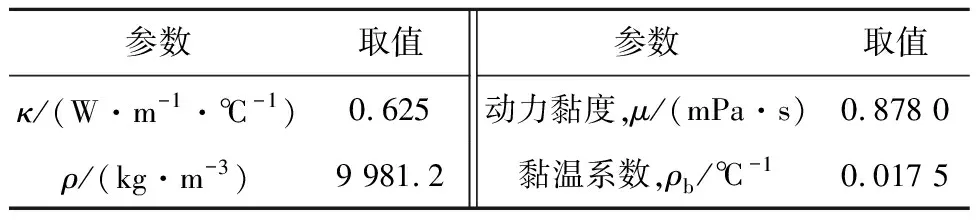
表3 清水介质26 ℃性能参数Tab.3 Properties of water media at 26 ℃
(1) 由于密封端面处的对流换热系数远大于密封环背面,故假设密封环背面S1和S11为绝热面.
(2) 假设流体域边界S12和S14表面温度均匀分布,密封环边界S2~S10与周围环境发生对流换热.
(3) 假设密封端面产生的热量均匀分布在WR和WS接触面的每一侧,且由于密封端面间液膜厚度较小,故忽略液膜的对流换热作用.
(4) 由于本案例泄漏量小于机械密封的标准要求,故忽略介质泄漏带走热量的情况.
(5) 忽略热辐射、密封介质物性随温度的变化以及流体的相态变化,此时傅里叶定律可用于密封环和界面处的工作流体.
密封端面传热和受力边界如图2所示.动环底面S1受弹簧力和密封介质压力共同作用与固定安装的静环紧密贴合,静环底面S11为绝热边界且施加固定约束.密封环外径与密封介质发生接触的边界W1~W7受介质压力po作用,且与介质进行对流换热;密封环内径与大气发生接触的边界S2~S10受大气压力pi作用,且与大气进行对流换热.
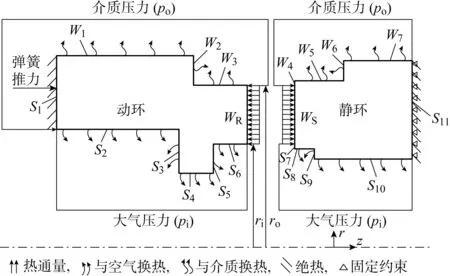
图2 密封环热力边界条件Fig.2 Thermal boundary conditions of seal ring
假设密封环与大气对流换热系数不变,其与大气接触的边界S2~S10的对流换热系数由下式确定[7],与密封介质接触的边界W1~W7采用Fluent自设参考值计算对流换热系数.静环受动环转动的影响,其对流换热系数取动环对流换热系数的1/3[8],即
(1)
式中:h为密封环空气侧的对流换热系数;kf为密封环材料的热传导数;ReD为空气的雷诺数;Pr为空气的普朗特数;D为密封环各边界的直径.
1.2 数学模型
1.2.1热源计算 在接触式机械密封实际运行过程中,密封端面大多处于混合摩擦或者边界摩擦的状态,采用Luan等[36]的表达式推导计算密封环相对运动端面所产生的热量:
Qf=pcAffωr
(2)
式中:pc为密封端面接触压力;Af为密封接触端面的面积;ω为动环旋转的角速度;f为端面的平均摩擦因数;r为半径.
当机械密封稳定运行时,密封的开启力和闭合力保持平衡,有:
Fc=Fo=Fsp+[p2B+p1(1-B)]Af=
pmAf+pcAf
(3)
式中:Fo为开启力;Fc为闭合力;Fsp为弹簧力;p1为大气压力;p2为密封流体介质压力;pm为密封端面流体平均膜压.可以推出:
pc=psp+p2B+p1(1-B)-pm
(4)
式中:psp为弹簧比压,即密封环接触端面单位面积上所承受的弹性元件作用力.
目前很多针对机械密封端面摩擦生热的研究均采用式(4)中的pc进行计算[37-38],如果采用流体平均膜压pm,则相当于等价忽略了端面摩擦状态沿径向的变化,使得流体膜压与接触压力沿径向均为常数,以此来计算端面间的摩擦生热显然不够准确,应考虑流体膜压和接触压力的实际分布情况.实际上,密封端面任一区域的生热功率应由端面接触压力与滑动速度共同决定.
图3为密封端面液膜压力的近似分布示意图.对于中等黏度的液体(如水),流体沿径向的压力近似呈线性分布,高黏度液体(如油)则呈现凸形分布,低黏度液体(如液态烃)则呈凹形分布[39].本文选用的工作流体为清水,端面液膜压力可近似认为呈线性分布.
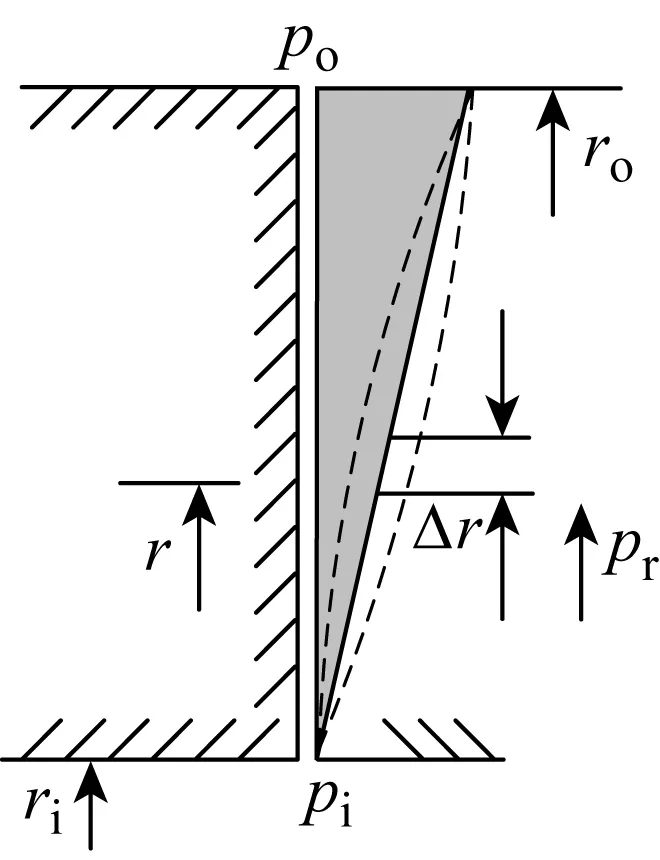
图3 密封端面液膜压力分布Fig.3 Liquid film pressure distribution on seal face
设密封接触端面沿半径方向r处,宽度为Δr的环形面积上的膜压为pr,根据相似关系,pr可表示为
(5)
式中,r1、r2为半径取值位置.
单位密封面上所承受的开启力(pr+pc)沿半径方向应均匀分布,否则密封端面间将产生倾覆力矩使密封环发生偏转.故半径r处密封端面上的接触压力为
pc=psp+p2B+p1(1-B)-
(6)
代入式(2),可得半径r处宽度为Δr的环形面积上的产热功率为
(7)
单位面积的热功率为
(8)
将上式编入UDF程序并加载到密封端面(即WR,见图1),模拟过程中将此面视为摩擦面.采用接触热导率法[40],在密封环接触单元上设置热传导率值为103,实现热量在动、静环间的自动分配.
1.2.2交变工况数学表达式 深潜器在实际下潜与上浮的运行过程中所受工况条件极为复杂,工作介质的压力、密度、主轴转速、支承弹簧力或主轴挠角均可能因下潜深度和叶轮的工作状态而发生改变.pv值是机械密封选型和设计时经常用到的重要参数之一[39],二者的乘积可以衡量机械密封承载能力的高低,故重点关注压力、线速度对深海涉水装备用机械密封性能的影响.其中,p分为两类,一是介质压力pf,二是密封端面比压pc.本文以pf为基础(下文p均指pf),考虑交变工况的具体函数表达,假定交变工况pv值的变化是线性的,分别通过机械密封介质压力或主轴转速的变化,使pv值以一定的幅值和频率上下波动,并比较二者各自的影响作用.
因假定pv值的变化是线性的,所以介质压力与转速的时变函数在每个周期内的极值点左右两侧的斜率不一致,即极值点处的导数不存在.程序设计中,可用循环与分段函数直接表达这种周期性变化,但仿真中模拟设置边界条件以及试验研究中调控工况参数时,需要以单一的数学表达式f(t)表示摩擦因数f在时域中的变化情况.
根据无穷级数理论,任何周期函数都可用正弦和余弦函数构成的无穷级数表示,称为傅里叶级数.周期为Γ的函数f(t)展开成sint和cost函数和的形式,可表示为
(9)
(10)
(11)
(12)
式中:a0/2为常数项;an、bn分别为第n项时正、余弦分量的系数.
根据傅里叶级数对深海交变工况的形式进行简化设计,假定工况摩擦因数f在初始时刻由平衡位置开始作周期性变化,故为正弦级数.在保证计算精度的前提下,展开至级数前6项,摩擦因数f关于t的表达式如下:
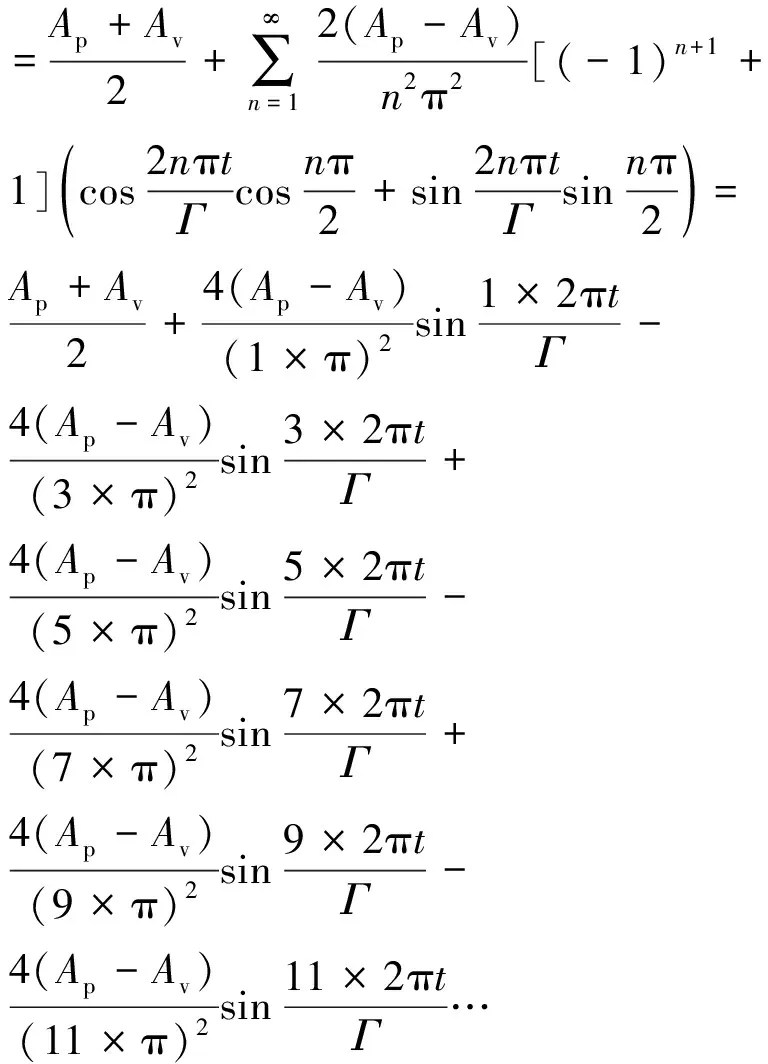
(13)
式中:Ap为参数变化过程中的波峰值;Av为参数变化过程中的波谷值.
根据深海推进器实际运行参数,设机械密封稳定运行时主轴转速n′=3 600 r/min,腔内介质压力p=400 kPa,本文采用控制其中一个参数不变,另一个参数进行有规律的周期性变化模拟深海工况条件.定义无量纲振幅M=(Ap-f0)/f0,其中f0=0.5(Ap+Av)为参数在平衡位置的值,并分别取参数变化振幅M为0.1、0.2、0.3、0.4和0.5,变化周期Γ为1.6、3.2、4.8、6.4和8.0 s.
以交变介质压力工况为例,表4展示出了交变 振幅的具体呈现形式, 表5展示出了交变周期的具体呈现形式.在稳定工况参数设置的基础上,转速恒为 3 600 r/min,介质压力发生周期性波动,振幅越大,压力波动的幅值越大,周期越小,压力波动的频率越快.同理,易得交变转速工况波动形式.

表5 交变周期形式Tab.5 Forms of alternating period
2 数值模拟与分析
2.1 网格无关性验证
考虑网格数量对计算结果精度的影响,首先进行网格无关性验证,结果如表6所示,以最后一组网格数所得端面平均温度作为对比基准,计算得到不同网格数与基准之间的相对偏差.综合考虑,本文采用的网格单元数为 14 126,节点数为 14 333,其中 流体域网格数为 7 428,节点数为 7 635,动环网格数为 4 022,节点数为 4 184,静环网格数为 2 676,节点数为 2 793,流体域近壁面无量纲参数y+值为31.08~66.16.
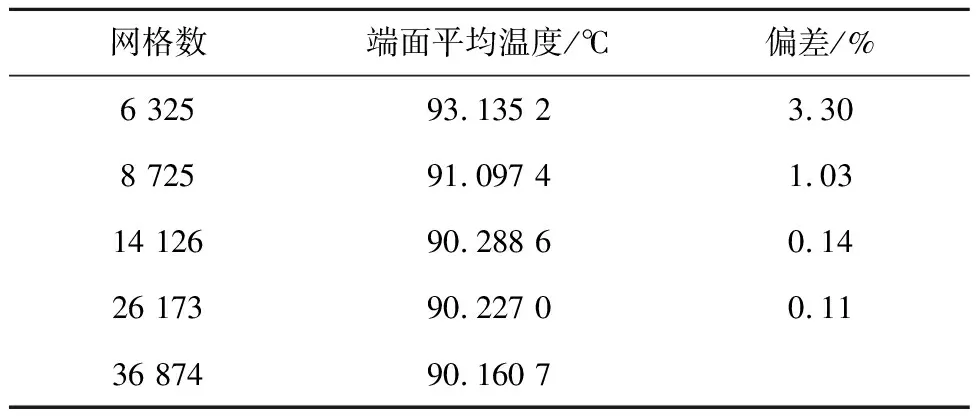
表6 网格无关性验证Tab.6 Grid independence verification
2.2 交变工况对密封端面温升的影响
图4为在振幅M=0.5,周期为3.2 s的交变工况下密封环接触端面平均温度(T)-时变曲线.其中,图4(a)为交变介质压力及其工况下端面平均温度的变化情况,图4(b)为交变转速及其工况下端面平均温度的变化情况.从图4可以看出,在交变载荷作用下,端面平均温度分布均表现出明显的瞬态交变特性,接触端面平均温度均随工况参数变化呈现波动上升的趋势,起始端面平均温度迅速上升,随着时间的推移温升速率逐渐减慢,最后达到某一稳定值后趋于动态平衡状态.对比图4(a)和图4(b)可知,当M=0.5时,相比于交变介质压力工况,交变转速工况下密封端面平均温度的交变特性更为明显,其波动幅值更大.结合式(7)可知,这可能是因为介质压力的改变,导致密封端面接触比压不断变化,从而间接影响端面摩擦生热,而摩擦热与转速大小呈正相关.同时可以看出,由于瞬态积分效应的影响,端面平均温度的峰值相比于交变介质压力和交变转速均表现出一定的滞后性.
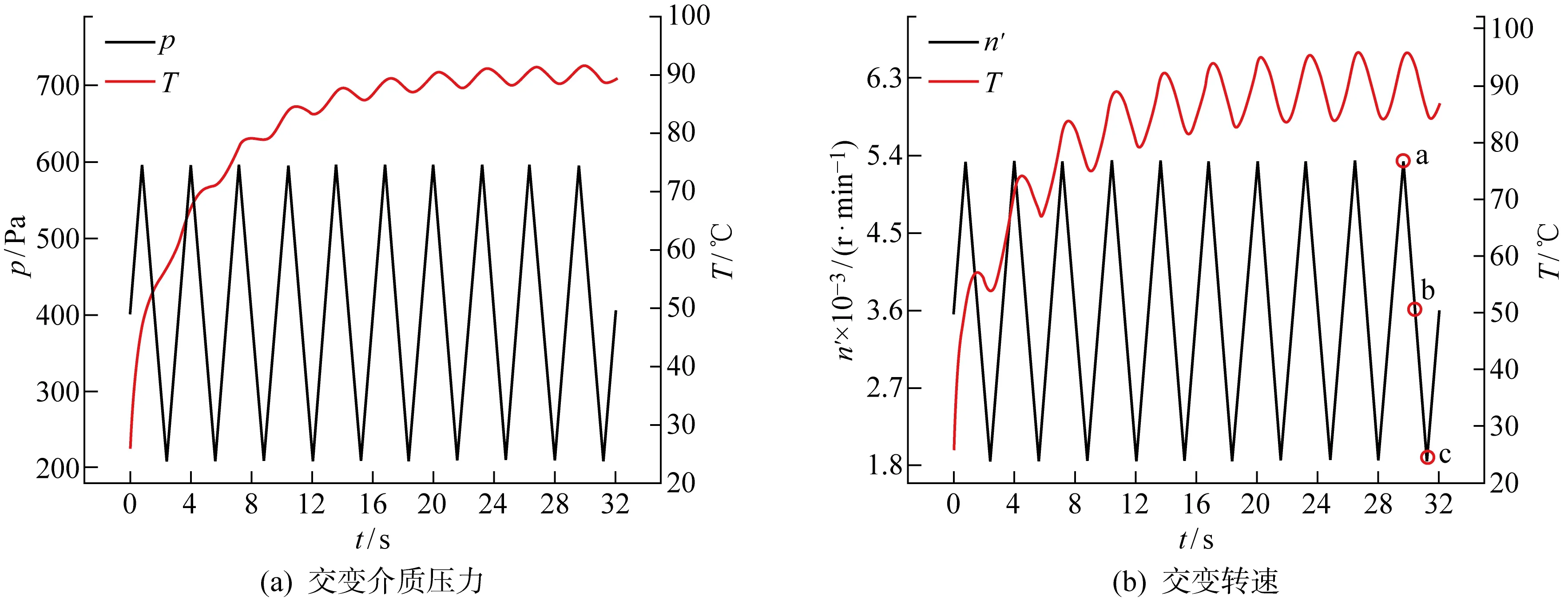
图4 M=0.5交变工况下密封端面平均温度时变曲线 Fig.4 Time-varying curve of average temperature of seal face under an alternating condition of M=0.5
对比不同工况下密封环瞬时温度场云图可知,密封端面最高温度均靠近密封端面内径处.选取图4(b)中交变转速工况最后一个交变周期不同时刻密封环端面温度沿径向分布曲线,如图5所示;并取转速由峰值到平衡值再到谷值,即如图4(b)中a、b、c处3个时刻对应密封环的瞬时温度场分布云图.从图5和6中可以看出,在运行过程中密封端面最高温度区域位于动、静环接触端面靠近内径处,温度沿径向逐渐降低,这是因为密封环的外周与冲洗介质接触,散热条件较好,而密封环内径侧与大气接触,散热性较差.密封环内温度成抛物线型沿着轴向外径扩散,靠近密封端面的区域温度梯度大,远端较小,这是由于受密封环自身热传导及其边界对流换 热的双重作用的影响.M106K动环的对流换热较强,平均温度较低,且SSiC静环的导热系数较高,故静环的温度梯度小,温度分布较为均匀.
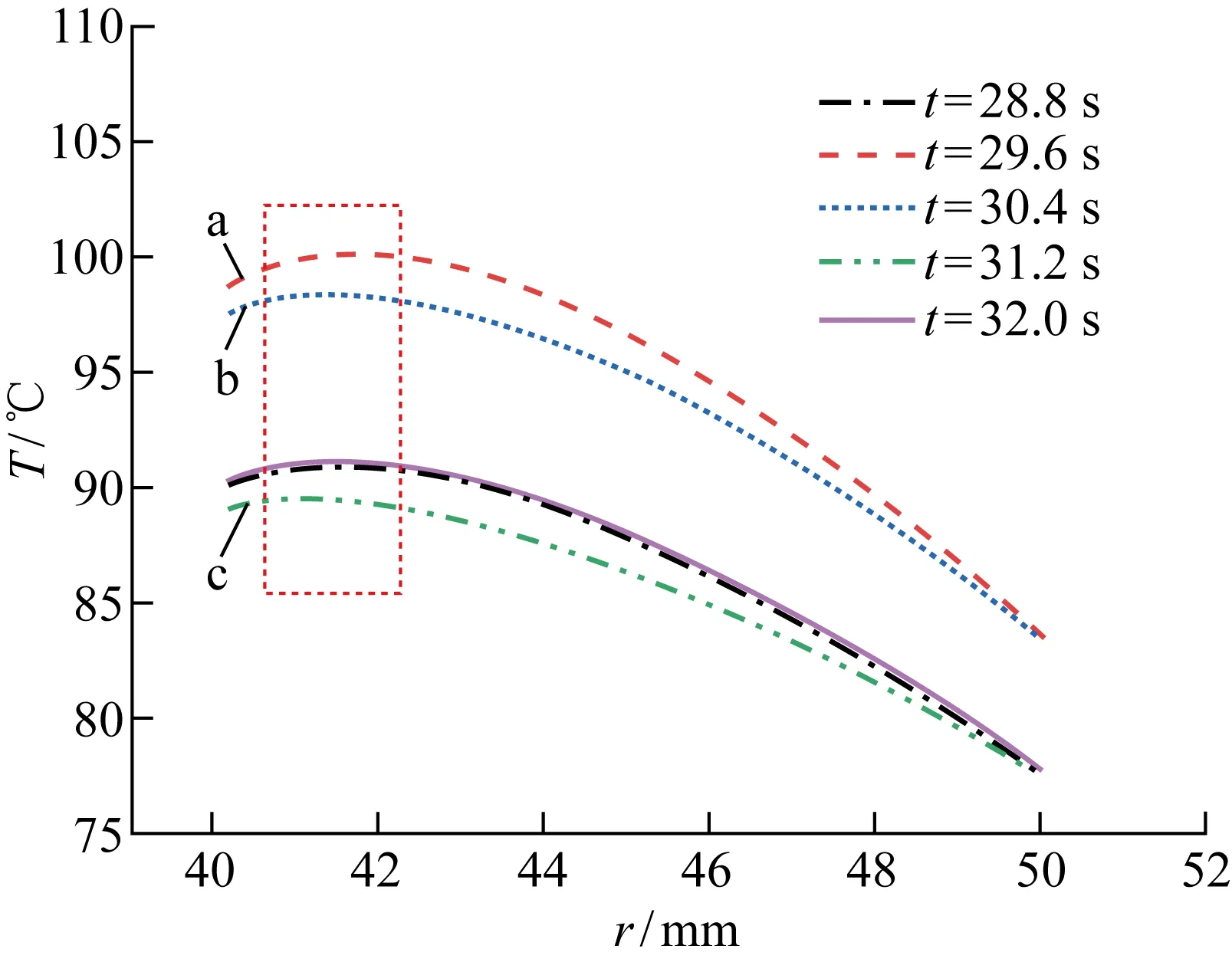
图5 M=0.5交变转速工况下的密封沿径向的端面温度Fig.5 Radial temperature of seal face at an alternating speed of M=0.5
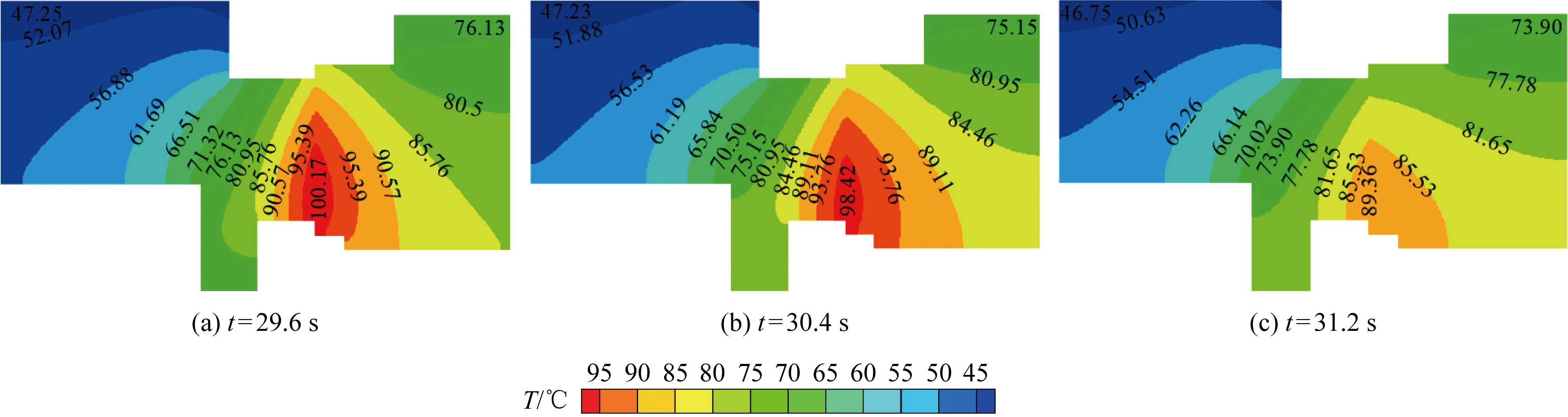
图6 M=0.5交变转速工况下的密封环温度场分布云图Fig.6 Contour map of temperature field of seal ring at an alternating speed of M=0.5
稳定工况和不同振幅交变介质压力以及转速工况下端面平均温度时变曲线如图7所示.其中,图7(a)是交变介质压力工况下的端面平均温度变化曲线,图7(b)为交变转速工况下的端面平均温度变化曲线,交变工况周期均为3.2 s.由图7可见,稳定工况下(n′=3 600 r/min,p=400 kPa),密封端面平均温度随时间的变化可表示为一条光滑上升的曲线;初始阶段,端面平均温度迅速上升,随着时间的增加,端面温升速率减小并趋于稳定.对于交变工况,随着交变参数振幅的增大,端面摩擦热增加,平均温度波动的幅值也随之增加,相较于稳定工况,交变转速工况下端面平均温度最大偏移为16.06%,交变介质压力工况下端面平均温度最大偏移为3.93%,交变转速工况下端面平均温度随振幅增加其波动程度更为显著.
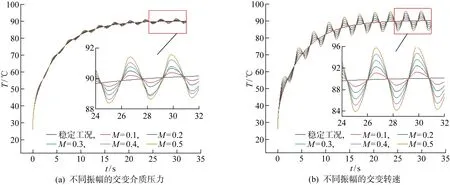
图7 不同振幅的交变工况下密封端面平均温度时变曲线Fig.7 Time-varying curve of average temperature of seal face under alternating condition at different amplitudes
稳定工况和不同周期交变介质压力和转速工况下密封端面平均温度时变曲线如图8所示.其中,图8(a)为交变介质压力工况下密封端面平均温度曲线,图8(b)为交变转速工况下密封端面平均温度变化曲线,交变振幅M均为0.2.由图8可见,在转速相同的情况下(n′=3 600 r/min),密封端面平均温度呈波动上升的趋势,波动趋势与交变周期有关,周期越短,端面平均温度上下波动的频率越快,反之则越慢.密封端面的温度在不同交变周期工况下,其上下波动的幅值并未出现明显的差异,相较于稳定工况,交变转速工况下端面平均温度最大偏移为7.76%,交变介质压力工况下端面平均温度最大偏移为1.91%,再次验证转速交变相较于介质压力交变更容易影响密封端面温度波动.由此可知,转速的瞬时变化对深海推进器机械密封的密封性能和使用寿命具有极大考验.
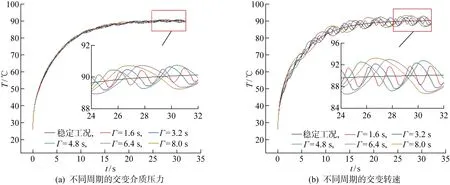
图8 不同周期的交变工况下密封端面平均温度时变曲线Fig.8 Time-varying curve of average temperature of seal face under alternating condition in different periods
3 试验研究
3.1 交变工况机械密封试验装置
围绕深海涉水装备在恶劣交变工况下运行时的密封性能开展了深海推进器机械密封拟实试验,实时监测密封端面温度变化及泄漏情况,观察并测量试验后端面形貌及磨损程度.本试验装置系统主要由试验密封腔、轴承辅助系统、供液调压系统、动力控制与传动系统以及数据采集与控制系统组成,如图9所示.图中,N1~N5为流向顺序.
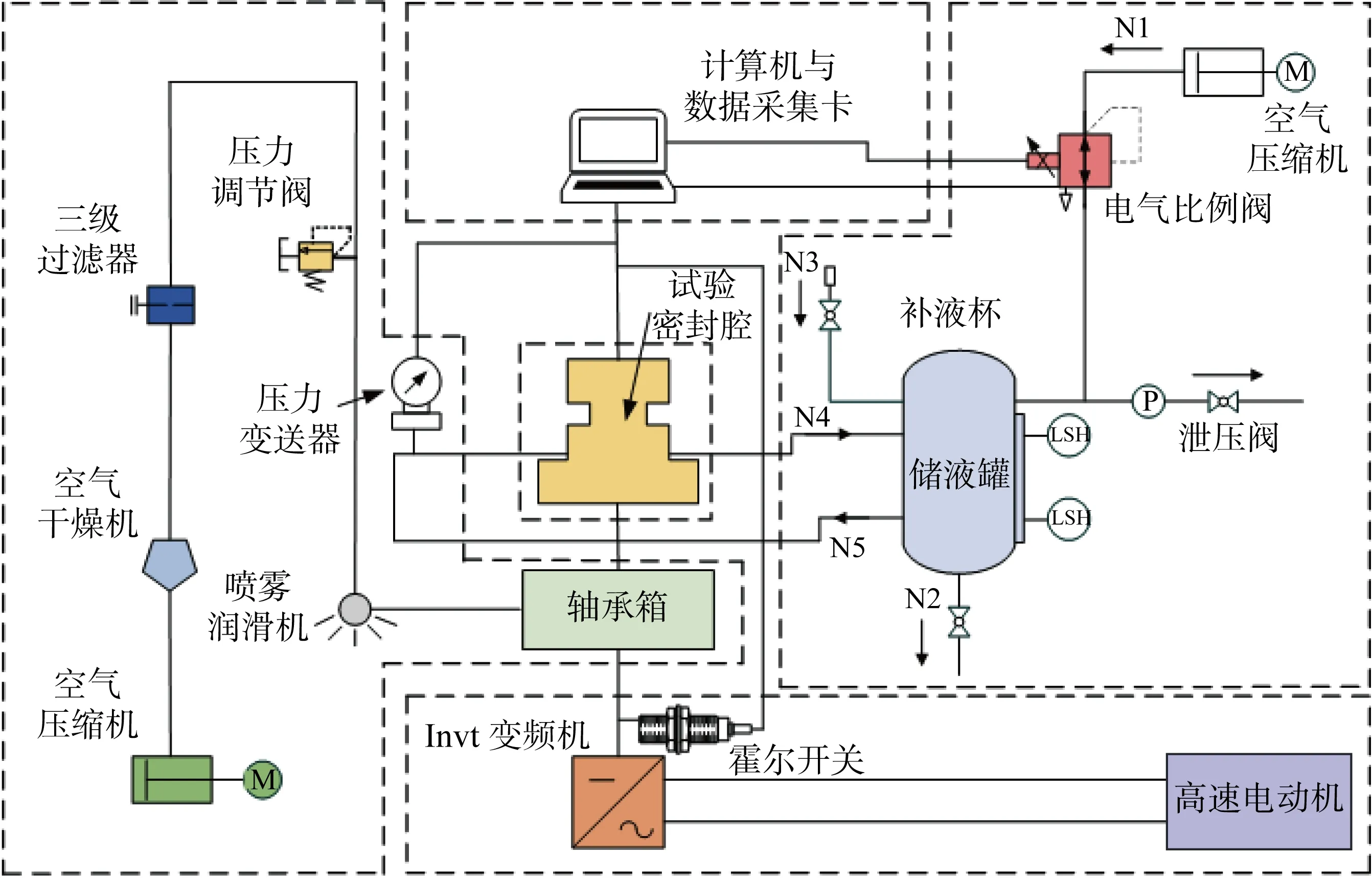
图9 交变工况机械密封试验装置系统示意图Fig.9 System diagram of mechanical seal test rig under alternating conditions
试验密封腔实物装置如图10所示,该装置为背靠背双端面密封,两道密封结构相同,每道结构主要包括动环、静环、动环座、静环座、O形圈和弹簧等.密封腔内上端密封为主密封,试验所需相关数据从该道密封中获得,下端辅助密封的主要作用是防止密封腔内密封介质污染轴承.轴承辅助系统的作用是给轴承提供润滑,以及监控轴承在高速运转过程中的稳定性和可靠性.供液调压系统主要通过基于LabVIEW自主开发的压力检测与控制程序,给密封腔体提供一定压力的恒温密封介质,通过比例阀,根据数据采集卡输出的电信号连续地对空气压缩机的供气压力进行控制,进而可改变储液罐内液体的实时工作压力.动力传动系统的主要作用是调控和监测电动机转轴的转速.数据采集与控制系统主要测试试验过程中的工况参数和密封性能参数信号.
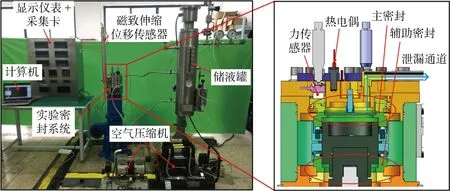
图10 试验装置图Fig.10 Diagram of test rig
3.2 试验测试
试验中动环材料选用M106K,静环材料选用SSiC,密封环尺寸及物理参数详见表1和表2.密封介质的初始温度均为26 ℃.在给定工况下(见表7~9),每组试验测试时间均为2 h,表中M(p)和M(n′)分别表示介质压力和转速的振幅变化.试验过程中采用精度为±1.5 ℃的K型热电偶对静环端面温度进行测量,静环背面取3处位置开盲孔用于埋设测温热电偶,如图11所示,测量位置分别为静环内、中、外径各距离静环端面1 mm处,环境温度保持(26±1) ℃不变.为减少试验误差,每组试验均重复3次以确保试验结果的可靠性.考虑霍尔元件测量电动机转速的方法为间接测量法,即对脉冲信号进行处理,测定瞬时转速变化时存在一定的时间滞后,约为3~5 s,此外,储液罐中压力的调节采用控制空气压缩机输出端压力的方式,气体加压与泄压相较主轴转速调节的机械作用方式更慢,因此试验中工况交变周期的变化范围设计为16~48 s.试验前后动静环表面形貌由LEXT OLS5000型3D测量激光显微镜测得,端面粗糙度由德国布鲁克DEKTAK·XT型台阶仪测得.

表7 第1组试验Tab.7 The first set of test conditions

图11 静环背面示意图Fig.11 Schematic diagram on the back of stationary ring
3.3 试验结果与讨论
3.3.1交变工况对端面温升的影响 图12为试验过程中静环端面沿径向取内径、中径和外径3处不同位置平均温度的时变曲线图.其中, 图12(a)为稳态工况下静环端面沿径向的温度时变曲线图,即表6中的1#试验结果;图12(b)为交变转速工况下静环端面沿径向的温度时变曲线图,即表8中的11#试验结果.由图12可知,在不同工况下静环端面温度均呈现先快速上升、后趋于平缓的趋势,这是因为初始时密封环温度与环境温度相同,开机启动后,动环高速旋转产生摩擦热,密封端面温度快速上升,机械密封在运行初期存在明显的磨合阶段[41],随着不断磨合,石墨逐渐脱落并转移至碳化硅表面形成自润滑层,造成端面间的摩擦因数一定程度上降低,同时密封端面微凸体弹性接触比例增大,而塑性接触比例下降,意味着机械密封端面间的弹塑性接触压力下降,也降低了端面发生严重黏着磨损的可能性.由于密封端面摩擦因数与接触压力的降低,端面间的产热功率也随之降低,故端面温度呈现出随时间减速上升的变化规律.当产热功率与冲洗介质的散热效率相等时,端面温度将趋于稳定.此外,还可以看出,在稳态和交变工况下,静环端面温度均为内径处最高、外径处最低,这是因为外径处与冲洗介质接触,散热条件较好,但因密封环接触端面较窄,仅为1 mm,所以内、外径温差较小,均保持在约1 ℃.
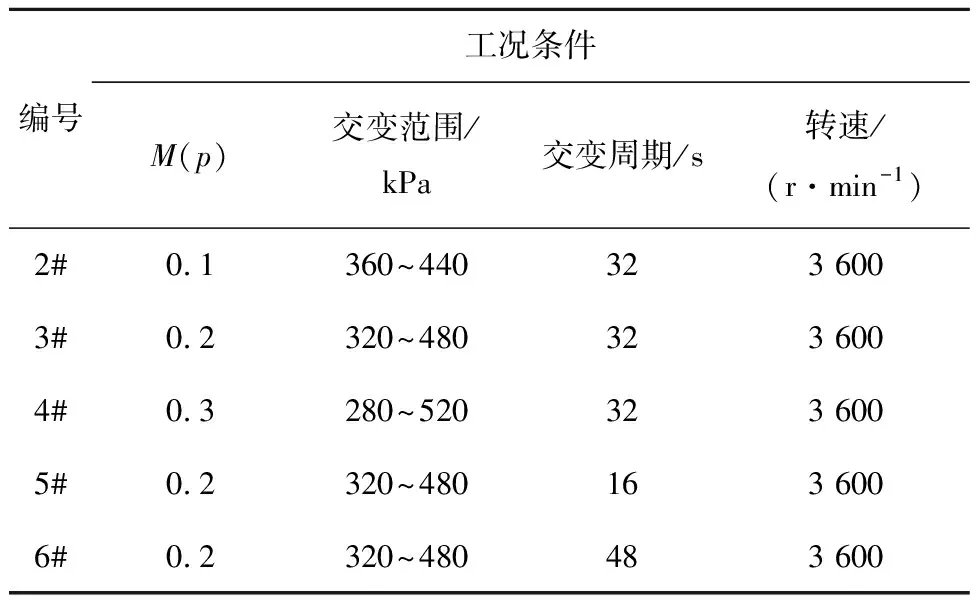
表8 第2组试验Tab.8 Second set of test conditions
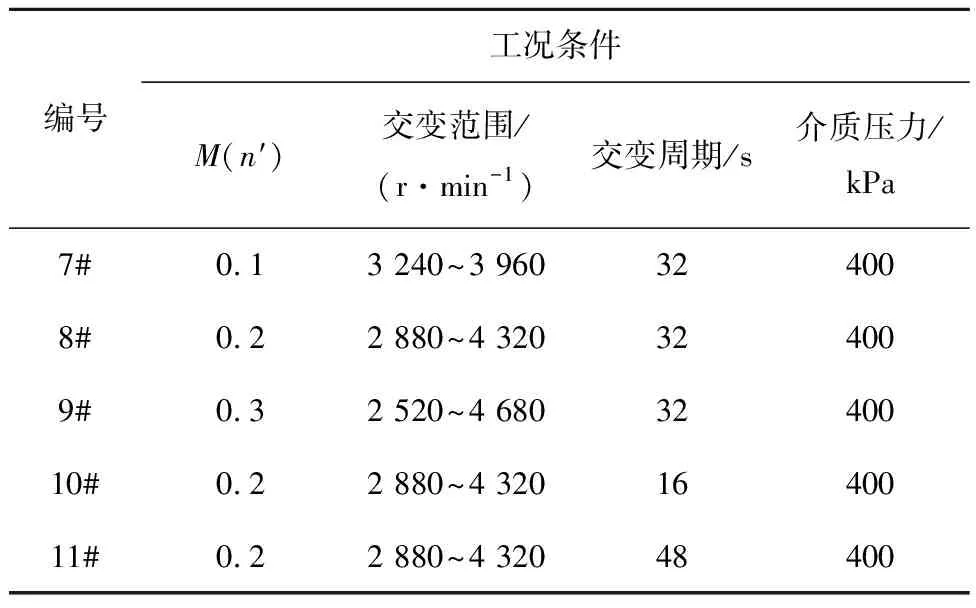
表9 第3组试验Tab.9 Third set of test conditions
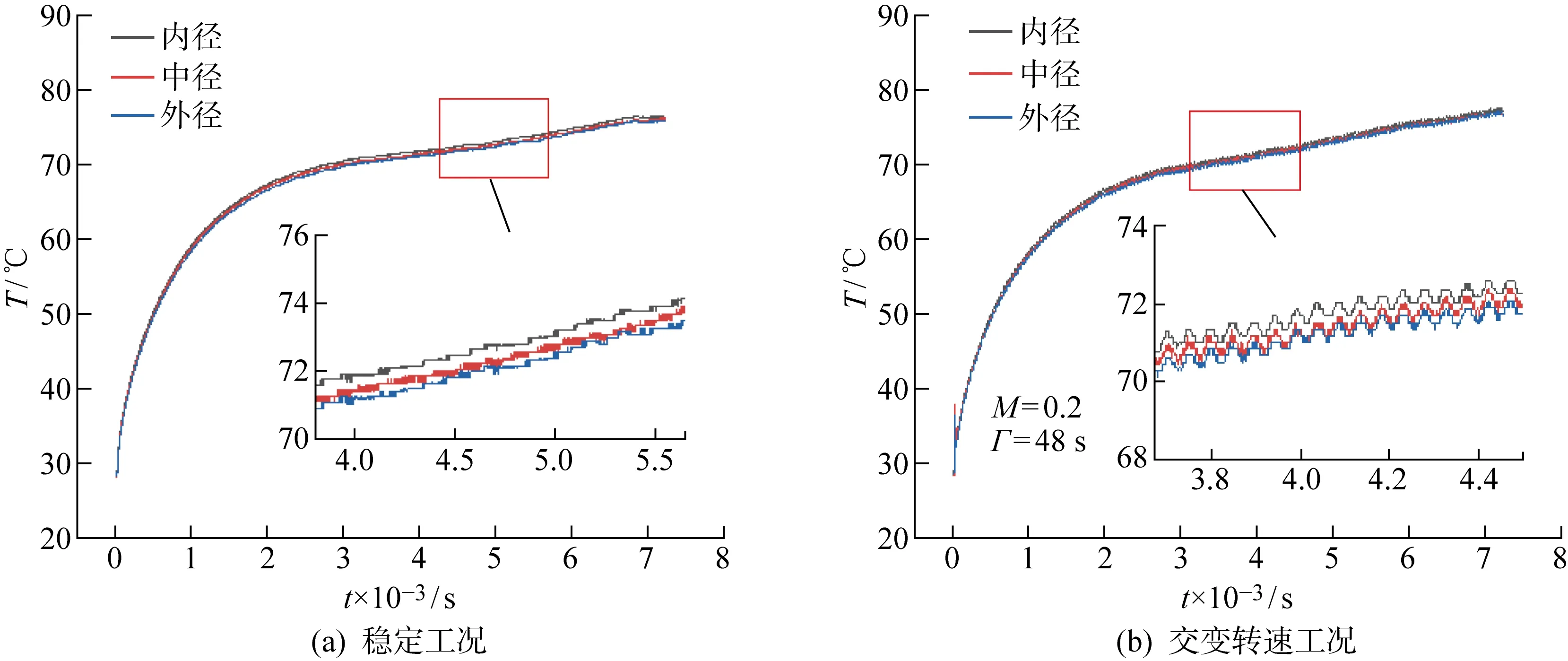
图12 稳定和交变工况下密封端面沿径向的温度曲线Fig.12 Temperature along radial direction of seal face under stable and alternating conditions
对比图12(a)和图12(b)可以看出,交变工况下,静环端面内、中、外径温度随工况瞬时波动的趋势相同,均表现出明显的交变特性,且温度波动周期与交变工况波动周期基本吻合,对不同交变工况动静环端面温度时变数据分析均可得到相同结果,此处不再赘述.
根据以上试验结果,将静环端面内径、中径和外径3处位置的温度取平均值进行进一步分析.如图13所示,图13(a)为稳定工况与振幅M=0.3、交变周期Γ=32 s时,交变介质压力和交变转速工况下静环端面平均温度时变曲线,即1#、4#和9#试验结果;图13(b)为稳定工况与转速振幅M=0.2、介质压力为400 kPa时,在不同交变周期工况下的静环端面平均温度时变曲线,即1#、8#、10#和11#试验结果.由图13(a)可知,相较于稳定工况,交变工况下静环端面平均温度均呈波动上升的趋势,波动形式与交变工况波动的周期基本吻合.同时,交变振幅相同时,交变转速工况下端面温度曲线波动的幅度较大,其对端面平均温度的影响尤为显著,这是因为转速的变化会直接作用于配对摩擦副使得产热功率增加,而压力的变化除了改变闭合力外也同时影响端面开启力.因端面温升密封环可能会发生沿泄漏方向的收敛变形,增加介质压力同时也使进入密封间隙的流体增多,减少了固体接触承载的比例,一定程度上改善了润滑条件.由于压力的双向影响,振幅相同时,相对交变压力工况,交变转速工况对端面温度曲线波动的影响更大.
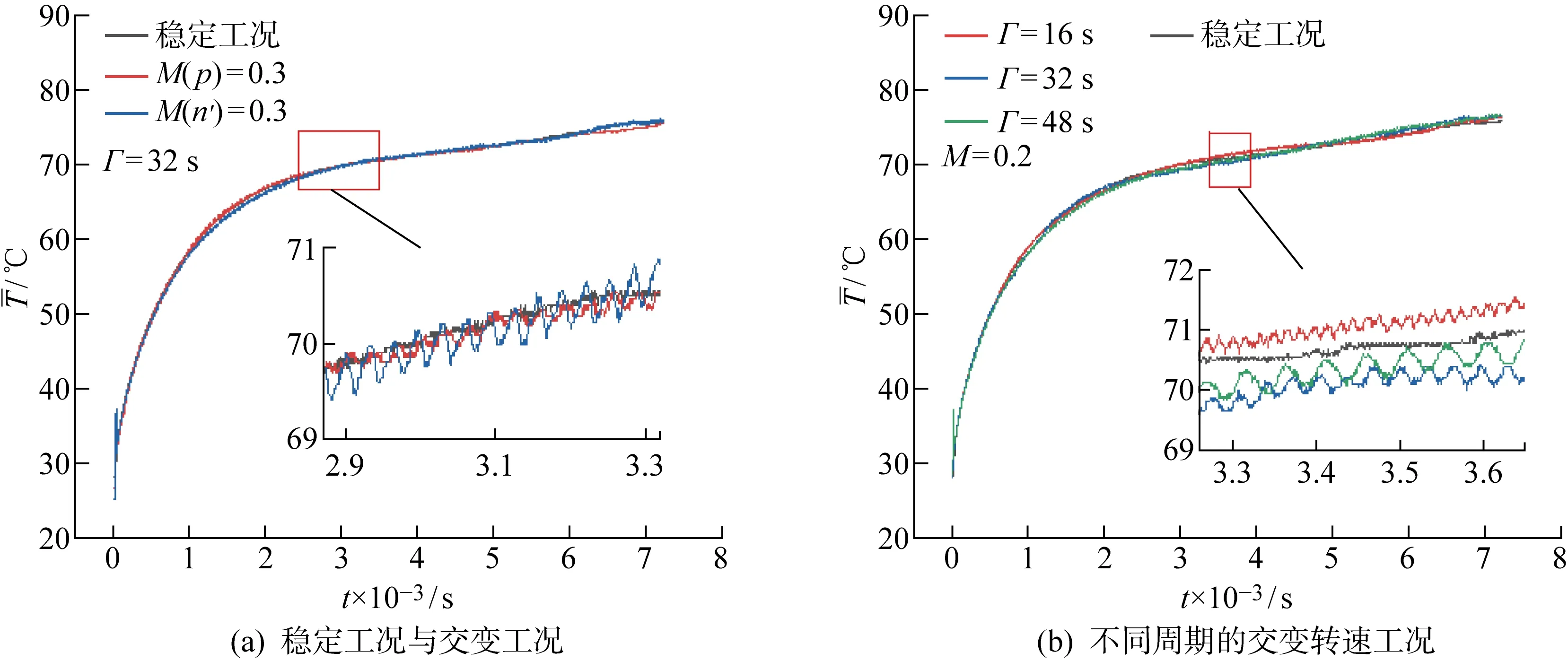
图13 密封端面平均温度时变曲线Fig.13 Time-varying curve of average temperature of seal face
图13(b)中结果表明,交变转速工况下端面平均温度时变曲线与稳定工况下的时变曲线整体趋势基本相同.交变转速工况下端面温度波动的频率与交变周期有关,工况的交变周期越小,端面温度上下波动的频率越快,反之则端面温度上下波动的频率越慢.此外,通过分析交变压力工况下静环端面温度时变数据可得上述相同结论,且振幅和周期相同的条件下,交变压力温度波动的幅值均小于对应条件下交变转速工况端面温度波动的幅值.综上所述,试验所得密封端面温度情况与模拟计算所得到的密封端面温度变化特性结论一致,在一定程度上验证了数值模拟的准确性.
3.3.2交变工况对密封环表面形貌的影响 为了进一步揭示交变工况对机械密封性能影响,开展了密封端面表面形貌的试验测试研究.通过对比不同工况条件试验前后动环表面形貌发现,不同交变工况试验后M106K动环端面内径处均出现不同程度的磨损,如图14所示为交变工况试验前后动环端面沿径向的粗糙度(Ra)对比.其中,图14(a)为3#试验前后动环端面沿径向的粗糙度测试结果,图14(b)为8#试验前后动环端面沿径向的粗糙度测试结果,图中黑色线均表示试验前动环端面的粗糙度测试结果.由图可见,试验前动环端面初始状态平面度较好;试验后,动环端面粗糙度显著增大,靠内径处磨损较为严重.当交变振幅和周期均相同时,相对于交变压力试验工况,交变转速试验工况下的动环端面粗糙度明显较大.
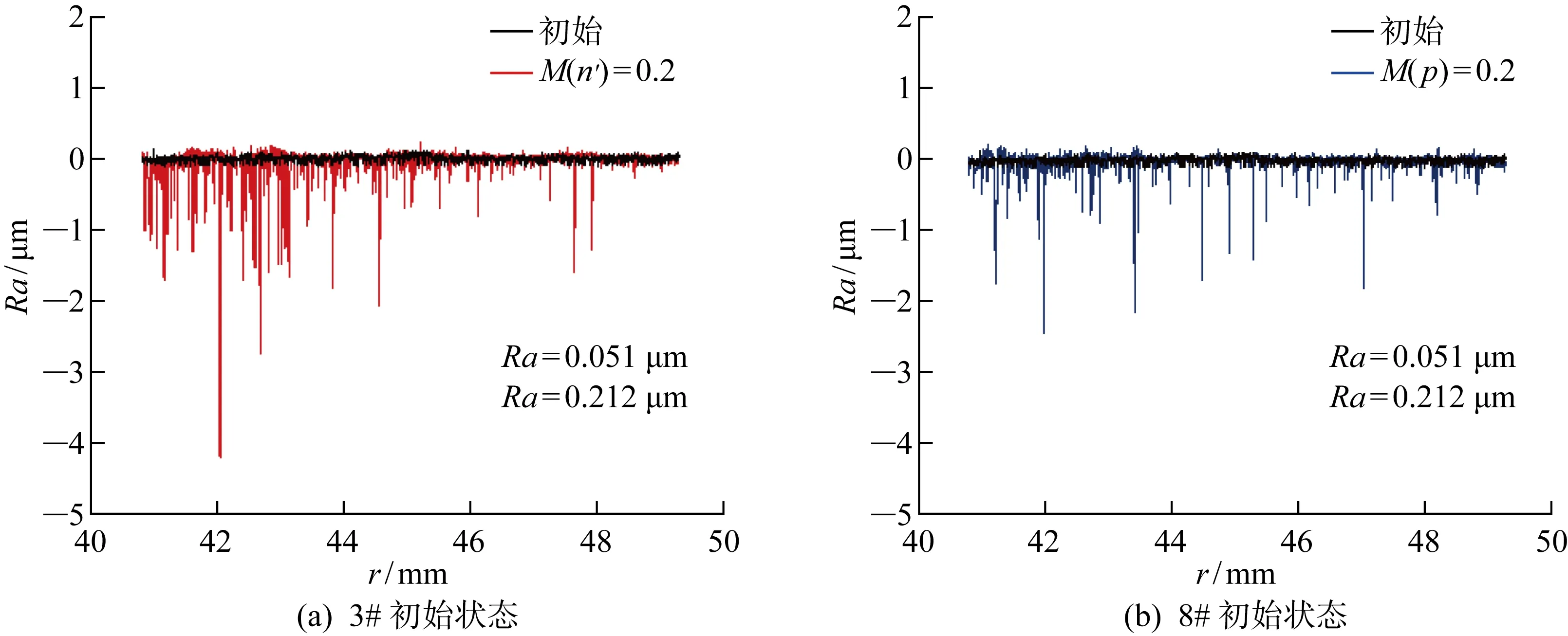
图14 试验前后动环端面沿径向粗糙度对比Fig.14 Comparison of radial roughness of end face of rotating ring before and after test
图15所示为使用激光显微镜放大5倍得到的不同工况试验后M106K动环端面形貌照片.由石墨和呋喃树脂的属性可知,图15(a)中颜色较浅部分为石墨基体,颜色较深部分为呋喃树脂填充物或未被填充的孔隙.对比图15(a)~(d)可知:试验前动环端面石墨基体较为密实,未见单独的石墨颗粒,试验后基体略显疏松. 1#试验后端面磨损较轻,出 现较浅的犁沟和凹坑;3#试验后端面犁沟和凹坑的数量及深度均略有增加;8#试验后动环端面磨损程度较为严重,出现密集且较深的犁沟.这是因为浸呋喃树脂是一种含有热固树脂的材料,在摩擦副运转过程中,较高的端面温度会致使M106K中的树脂析出和结块而形成游离磨粒,对动环端面造成局部磨粒磨损,当振幅和周期相同时,交变转速工况下密封端面的摩擦热影响尤为显著,端面温度波动的幅度更大,端面磨损现象更为显著.

图15 不同工况试验后M106K动环表面激光显微照片Fig.15 Laser micrograph of end face of rotating ring(M106K)after test under different conditions
为进一步分析动环端面的形貌变化及其特征,在激光显微镜下将试验后动环端面靠近内径处形貌放大50倍,如图16所示,以端面初始状态为基准0,磨损情况中正值表示磨损后端面变形量,负值表示磨损深度.可见动环端面粗糙峰基本被磨平,端面沿周向呈现出明显的磨痕.在稳定工况下,端面磨损程度较轻,出现较浅的犁沟和凹坑,在交变介质压力工况下,端面磨损加剧,呈现出深浅不一的犁沟,凹坑的数量也相应有所增加.在交变转速工况下,摩擦热影响尤为显著,动环端面磨损程度最为严重,这可能是因为工况的瞬时交变下SSiC-M106K摩擦副接触状态随之不断发生变化,浸渍石墨部分受高温碳化形成游离磨粒并存储在摩擦副表面,磨屑聚集,在密封端面造成三体磨粒磨损[42];交变工况加剧后,犁沟数量显著增加,且转速对端面接触状态的影响较介质压力的影响更大,交变周期相同时,随着转速振幅的增加,动环端面的磨损程度显著增加.此外,试验后部分静环表面出现多道环形黑色印记,这可能是因为石墨部分碳化脱落形成的游离微粒,在较高的端面比压作用下转移到碳化硅静环表面,形成黑色环带.由此可知,交变工况对深潜器用机械密封端面的磨损影响不可忽视.

图16 试验后动环端面形貌Fig.16 Morphology of end face of rotating ring after test
由于在不同工况下动环内径处磨损较为明显,故取动环端面靠近内径处3 mm宽度测定其在不同工况试验后的粗糙度数据,如图17所示.其中,图17(a)为不同振幅的交变介质压力和交变转速工况下动环端面内径处粗糙度,图17(b)为不同周期的交变介质压力和交变转速工况下动环端面内径处粗糙度.结合上述动环端面内径处形貌图分析可知:交变介质压力和交变转速工况试验后动环端面内径处磨损程度与交变参数的振幅呈正相关.振幅增大,磨损加剧,导致试验后石墨环端面粗糙度增大.相较于稳定工况下动环端面粗糙度,振幅为0.1、0.2、0.3时,交变介质压力工况下动环端面粗糙度分别增加37.8%、56.8%、113.5%,交变转速工况下动环端面粗糙度分别增加97.3%、147.3%、286.5%,不同交变周期对端面磨损程度的影响未见明显差异.振幅相同,交变周期为16、32和48 s时,交变介质压力工况下动环端面粗糙度最高增加147.3%,交变转速工况下动环端面粗糙度最高增加223.0%.由此可知,深海推进器在工况复杂多变条件下运行时,密封端面易发生过度磨损,大大缩短了机械密封的使用寿命,且转速的瞬时变化更易加剧密封端面的磨损程度.
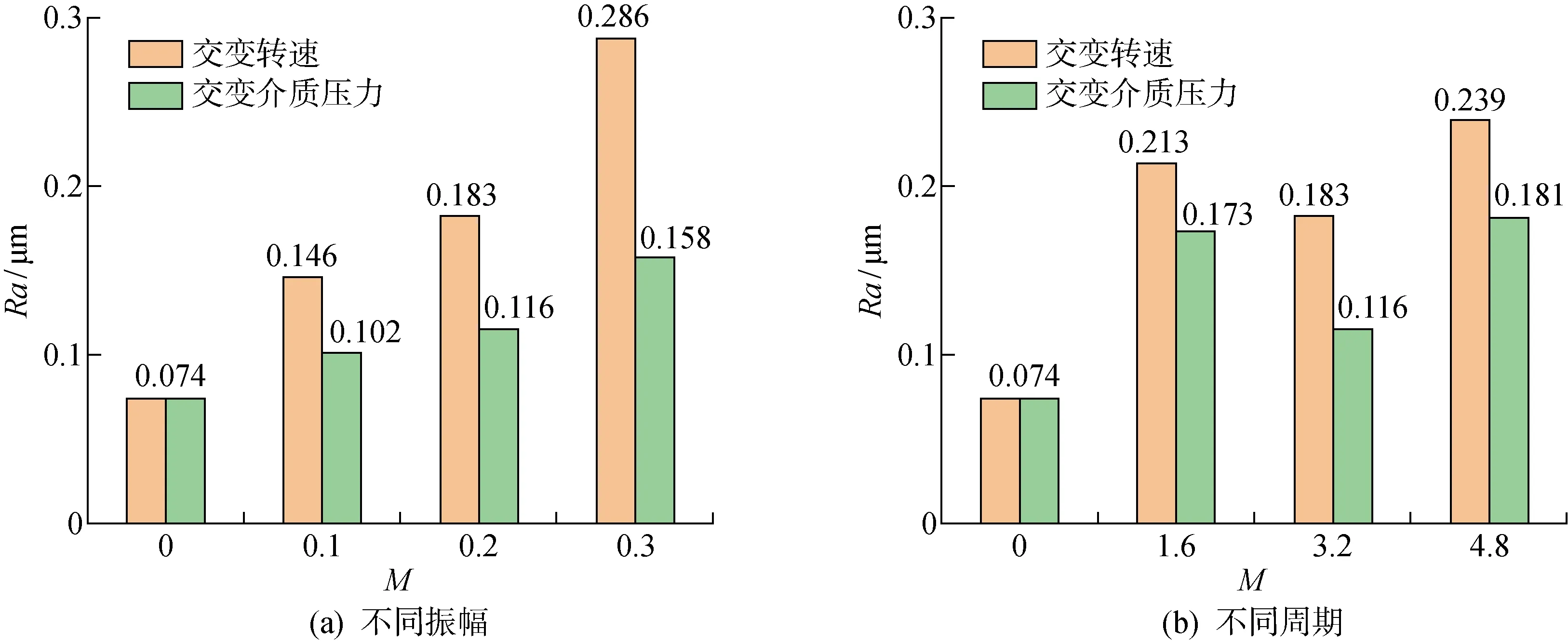
图17 动环端面内径处粗糙度Fig.17 Roughness at inner diameter of end face of rotating ring
综上所述,交变工况使得摩擦副接触状态不断变化及端面温度不断波动,浸呋喃树脂石墨在摩擦过程中易发生颗粒掉落或孔隙边缘刮擦,导致动环端面产生犁沟和凹坑而发生破坏,且摩擦副间存在的磨屑不利于润滑液膜的形成.当工况条件恶劣时,在周期性交变工况的作用下密封端面磨损程度加剧,极大降低了机械密封的密封性能,因此,应密切关注深海环境下复杂恶劣工况对机械密封产生的不良影响.
4 结论
通过对交变工况下深海涉水装备用机械密封进行端面温升和磨损特性的研究,可以得出以下结论:
(1) 对于稳定工况和交变工况,密封端面温度上升的整体趋势相同, 最高温度区域发生在密封端面靠近内径处;交变工况下密封端面温度随工况参数的变化呈波动上升趋势,表现出明显的交变瞬态特性;端面温度波动的幅值与工况参数的振幅呈正相关关系,相较于稳定工况,数值计算中交变转速工况下端面平均温度最大偏移16.06%,远高于交变介质压力工况下端面平均温度最大偏移量.在振幅相同、周期不同的交变工况下,交变周期越小,密封环端面温度波动的频率越快,交变转速工况下端面平均温度最大偏移7.76%,亦高于交变介质压力工况下端面平均温度最大偏移量.数值模拟和试验结果均表明转速的瞬时变化易对深海推进器机械密封的端面摩擦状态产生较大影响.
(2) 在稳定工况下,M106K动环端面磨损程度较轻;在交变工况下,动环端面出现大量凹坑和深浅不一且密集分布的犁沟,端面内径区域粗糙度变大,磨损程度较为严重,相较于稳定工况,交变转速工况下端面粗糙度最高增大286.5%,交变介质压力工况下端面粗糙度最高增大147.3%.交变工况下深海推进器机械密封更易发生不可修复的损伤,设计时需根据深海复杂多变的工况对机械密封进行合理结构优化(如表面涂层技术)以避免密封端面过早失效.

