基于斯蒂芬逊迭代的刚性电力系统时域计算交替求解法

黄钦雄，张俊勃，刘 洋

（华南理工大学电力学院,广东省广州市 510641）

0 引言

电力系统时域计算的数学模型是一组非线性的微分代数方程组（differential algebra equations,DAEs）［1］,常用的求解方法为交替求解法［2-3］。在新型电力系统背景下,大量可再生能源与电力电子设备接入电网,电力系统动态过程的时间常数差异增大,交替求解面临刚性问题,导致计算过程的收敛性与计算效率变差［4-5］。因此,如何提高交替求解法收敛性,使算法能够适应系统动态过程的强刚性,是新型电力系统背景下时域计算的关键问题。

影响交替求解法收敛性的因素包括迭代初值、积分步长以及DAEs 的预处理格式等。在迭代初值设置方面,可通过显式积分、人工神经网络等方法预估仿真变量初值,改善收敛性［6-7］。在积分步长方面,可基于方差和均值比最大值、局部截断误差等指标进行收敛性判别,实现自适应步长调整［7-10］。在DAEs 预处理方面,已有研究从发电机注入电流表达式中分离出不同形式的虚拟导纳,并将其并入网络节点导纳矩阵,以提高网络代数方程求解收敛性［1,11-12］,或通过在差分方程中引入差分方程对应的雅可比矩阵,以提高差分方程求解收敛性［13］。上述方法属于改善计算收敛性的通用方法,并不能改善系统的刚性问题。此外,DAEs 的预处理方法还存在不能兼顾算法收敛性与计算效率的问题。

刚性问题主要有适应系统刚性或弱化系统刚性两种解决思路。前者包括:1）采用数值稳定域与阶数更高的数值积分方法,如龙格-库塔法、Gear 法、泰勒级数法［14-16］等；2）缩小仿真步长或采用变步长方法以满足系统中动态环节的最小时间常数限制［17-18］。后者主要将系统分为刚性与非刚性部分,不同部分采用不同的积分方法进行求解,相关研究集中在如何对刚性与非刚性部分进行分组以及如何选取不同组合算法［19-25］。各种数值积分或缩小步长算法能够适应系统的刚性,但也存在积分格式复杂和积分区间增加的问题,限制了计算效率。同时,对系统进行刚性与非刚性的区分能够有效提高计算效率,但对不同仿真系统在计算之前都要进行系统划分,缺乏通用性,且划分不当时刚性部分仍存在迭代不收敛问题。

从不动点迭代理论出发,上述提高收敛性以及解决刚性问题的思路均可以理解为对迭代过程中迭代函数的导数矩阵进行优化,但这些做法都不改变迭代过程的收敛阶。若能对交替求解过程的迭代格式进行改进,在DAEs 有解的情况下提高迭代过程的收敛阶,扩大各仿真时步的收敛范围,则可能大幅提高迭代过程的收敛速度。

本文基于不动点迭代理论,分析交替求解法的迭代求解过程,在交替求解法流程中引入具有二阶收敛速度的斯蒂芬逊迭代,使交替求解法能够适应新型电力系统强刚性导致的时域计算收敛性恶化。

1 交替求解法的收敛性分析

1.1 DAEs 的交替求解过程

电力系统机电暂态仿真的DAEs 可表示为:

式中:x和u分别为状态变量和代数变量；Y为网络节点导纳矩阵；f为描述系统状态变量动态元件的微分方程；i为网络注入电流方程。

采用隐式梯形法将式（1）的微分方程离散化为差分方程后,计算n+1 时刻系统的状态即求解如下非线性代数方程组:

式中:下标n和n+1 分别表示仿真的第n和n+1 时刻；h为积分步长。

采用原始交替求解法对式（2）进行迭代求解时,迭代格式如下［3］:

式中:上标中k和k+1 分别表示第k和k+1 次迭代。

式（3）中差分方程和代数方程的交替求解可在牛顿法下进行理解。采用牛顿法进行n+1 时刻第k次差分方程与代数方程求解,可构造状态变量和代数变量的残差方程q、g如下:

根据残差方程可分别构造状态变量x和代数变量u的修正方程。在差分方程和代数方程的交替求解中,分别将u和x认为是已知量。因此,状态变量x的修正量Δx只与x有关,代数变量u的修正量Δu只与u有关,即

其中,矩阵A、D为雅可比矩阵,其表达式为:

式中:I为单位矩阵。矩阵A、D的具体表达式与系统中动态元件模型有关,其推导过程见附录A。

根据第k次迭代的解x(k)n+1、u(k)n+1,得到第k+1 次迭代的解为:

式（4）、式（5）、式（7）即为牛顿法下交替求解法的基本方程。

对于原始交替求解法迭代格式,可认为是在牛顿法下,对式（6）的雅可比矩阵进行一定简化。取A=I和D=Y,并将式（5）的修正方程代入式（7）后得到式（8）。

1.2 交替求解法的不动点迭代形式及新型电力系统背景下的收敛性恶化分析

将式（5）与式（7）联立,可得单次迭代中差分方程与代数方程交替求解的迭代公式为:

由式（6）可知,式（9）等号右侧的矩阵A、D分别为 关 于xn+1、un+1的 表 达 式,q(k)n+1、g(k)n+1也 分 别 为 关于xn+1、un+1的表达式。因此,式（9）具有标准的不动点迭代格式。状态变量x与代数变量u的迭代函数Φx(xn+1)、Φu(un+1)分别为:

不动点迭代的收敛性定理指出,若迭代函数Φ(x)在定义域S内有不动点x∗,Φ(x)的各分量函数具有连续偏导数,且Φ(x)的导数矩阵Φ′(x)的谱半径满足ρ(Φ′(x))<1,则对任意的x0∈S,迭代函数Φ(x)将收敛于不动点x∗［26］。

因此,在不动点迭代方法下,对差分方程、网络方程迭代求解的收敛性的讨论就转化为了对相应迭代函数谱半径大小的讨论。对于式（10）的不动点迭代函数,可得相应的导数矩阵Φ′x(xn+1)、Φ′u(un+1)为:

根据式（13）可知,在交替求解过程中引入矩阵A、D后,相应的不动点迭代函数导数矩阵中仅包含xn+1、un+1相关的高阶项,是相对稀疏的矩阵,故其具有较好的收敛性。这与文献［13］中通过引入A矩阵来最大限度地提高状态变量迭代收敛性的结论是一致的。

对于原始交替求解法,由于取A=I、D=Y,其相应的导数矩阵变为:

从式（15）中可看出,原始交替求解法的迭代收敛性由差分方程以及代数方程的迭代收敛性共同决定。同时,由于x、u在仿真过程中是时变的,导致导数矩阵谱半径时变,从而仿真系统的迭代收敛性会随仿真过程发生变化。

随机扰动的出现使得代数方程的导数矩阵中出现了与扰动相关的项,从而恶化了代数方程导数矩阵的谱分布。若计算过程中的收敛性主要取决于代数方程,则由于外部扰动不确定性的增强,将使计算过程的收敛性变差。

此外,在新能源与电力电子模型中,各类动态过程中广泛存在饱和、限幅等逻辑判断环节。在逻辑环节处理层面,在每轮状态变量与代数变量迭代计算结束后进行逻辑判断,根据限幅等环节的判断结果更新本次迭代得到的变量结果。由于系统方程与逻辑环节的求解不是同步进行的,实际计算需要在系统方程与逻辑环节间进行更多次的迭代才能同时满足系统方程与逻辑判断环节的约束,导致系统迭代求解的收敛性变差。

根据式（13）,在交替求解法中引入完整的矩阵A、D或矩阵A、D的近似矩阵,有助于减小谱半径,从而提高收敛性。一般来说,引入的A矩阵可分为以下3 种情况［27］:A=I/α,其中|α|<1 为松弛系数；A=diag(∂qn+1/∂xn+1)；A=∂qn+1/∂xn+1。引 入 的D矩阵根据注入电流对电压偏导表达式的等效程度不同,可分为虚拟导纳法、功角等效法［12］,相应的D矩阵表达式分别为附录A 中的D=Y+Yg和D=Y+Yg+Ytc,其中,Yg、Ytc分别为虚拟导纳法和功角等效法分离出的定常导纳矩阵。由于矩阵A、D与状态变量、代数变量相关,每次迭代都需要进行更新,将产生巨大的计算开销。实际计算中,通常采用非诚实牛顿（very dishonest Newton,VDHN）法,在不同时步间和迭代间传递矩阵A、D,以提高计算效率［9］。然而,采用VDHN 法对矩阵A、D进行近似后,实际矩阵A、D与当前迭代中采用的矩阵存在误差ΔA、ΔD。对于刚性系统,时间常数较小的动态环节对应的状态变量将在暂态过程中发生快速变化,使得ΔA、ΔD随暂态过程的推进变大,从而对谱半径的影响逐渐增大,导致仿真收敛性变差。因此,VDHN 法虽然提高了时域计算的效率,但代价是牺牲了一定的收敛性,且对于刚性系统将导致显著的收敛性问题。

1.3 提高交替求解法收敛性的讨论

通过上述分析可知,交替求解法收敛性恶化的机理以及提高交替求解法收敛性的方法可以在迭代函数导数矩阵谱分布与谱半径的视角下进行理解。由此,可将提高交替求解法的收敛性方法分为3 类:

1）限制系统最大仿真步长,从而整体性压缩导数矩阵的谱半径,对于刚性系统,需要将最大步长hmax缩小至10-4数量级或更小［24］；

2）采用合理的初值预估,使迭代初值更接近真值,从而减小误差；

3）优化迭代格式,使得导数矩阵的元素相对稀疏,有效改善谱分布。

这3 类方法中,减小步长能够有效改善收敛性,但增加了仿真时步数量,降低了计算效率；改善迭代初值能够缩小初始值与收敛解的差,但如果初值预测策略选取过于复杂,同样会增大计算量；优化迭代格式能够有效改善谱分布,但迭代格式的修正也在一定程度上引入了额外的计算量,降低了计算效率。此外,上述3 类方法在优化谱分布时,并不改变迭代过程的收敛阶。若能通过改进迭代格式提高交替求解过程的收敛阶,则能够在改善收敛性的同时兼顾计算效率。

2 基于斯蒂芬逊迭代的收敛性提升方法

2.1 斯蒂芬逊迭代过程

本节给出一种基于斯蒂芬逊迭代的交替求解收敛性提升方法,其本质是通过构造具有更高收敛阶的迭代格式,改善交替求解的收敛性。斯蒂芬逊迭代的基本原理如下。

针对迭代函数Φ(x),设其不动点为x∗,由x0出发构造迭代公式:

式中:下标i=0,1,2,…。

将式中的迭代函数Φ替换为Φx(xn+1)、Φu(un+1),即可得基于斯蒂芬逊迭代的差分方程与代数方程迭代格式。

已有研究证明,对于由不动点迭代函数Φ构造的斯蒂芬逊迭代函数Ψ,若Φ存在不动点在x∗的领域内存在、连续,且,则斯蒂芬逊迭代法至少具有二阶收敛性［28］。

采用斯蒂芬逊迭代后,交替求解法的计算流程如下:

步骤1:初始化n+1 时刻状态变量和代数变量的迭代初值x(0)n+1、u(0)n+1,迭代次数k=0。

步骤2:对于第k次迭代,若k=3i+1 或k=3i+2,则根据式（17）、式（18）依次计算第k次迭代的状态变量和代数变量结果x(k)n+1、u(k)n+1；若k=3i+3,则根据式（19）通过斯蒂芬逊迭代求解第k次迭代的状态变量和代数变量结果x(k)n+1、u(k)n+1。

步骤3:如果前后两次迭代的状态变量、代数变量最大迭代误差max {||x(k+1)n+1-x(k)n+1||,||u(k+1)n+1-u(k)n+1||}小于允许值ε,则认为本时步计算收敛,否则令k=k+1,返回步骤2,进入下一轮迭代。

基于斯蒂芬逊迭代的时域计算交替求解流程如图1 所示。由图可知,算法在求解流程上与原始交替求解法的区别在于,在两次常规状态变量与代数变量迭代之后,插入一次标量式的斯蒂芬逊迭代。

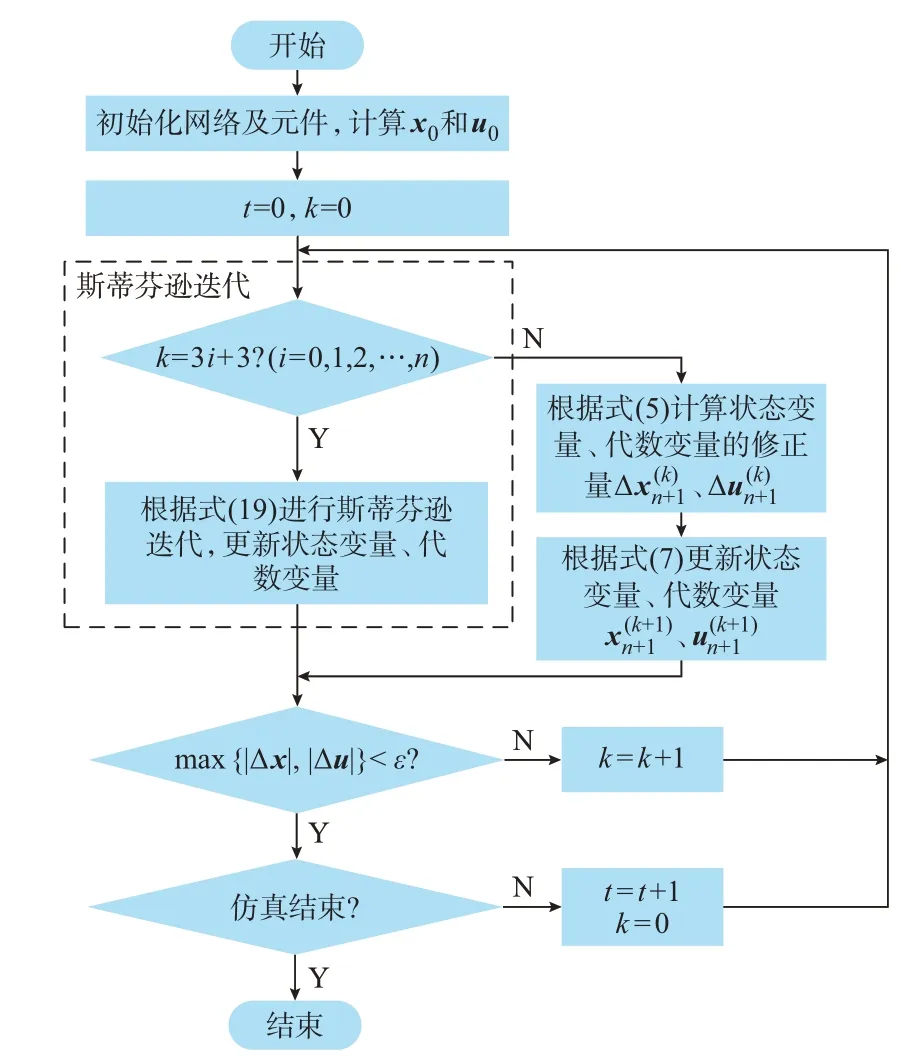
图1 基于斯蒂芬逊迭代的交替求解法流程图Fig.1 Flow chart of Steffensen iteration based alternating solving method

需要注意的是,在时域计算中,[x,u]为一组向量,相应的迭代函数Φ也为向量函数。在上述流程中,当k=3i+1 或k=3i+2 时,是以向量的形式进行迭代；当k=3i+3 时,是以标量的形式进行斯蒂芬逊迭代。因此,实际迭代过程比单变量迭代过程更加复杂,但标量式斯蒂芬逊迭代的总体过程是不变的。

此外,由于限幅、死区等逻辑判断环节的存在,实际DAEs 难以满足待求方程的二阶导数连续且存在的前提。实际求解时,将求解过程分解为“不含逻辑判断环节的方程求解”以及“根据逻辑判断环节更新系统变量”两个步骤。在“不含逻辑判断环节的方程求解”中,由于不需要考虑限幅、死区等带来的不连续及变量跳变问题,方程组仍满足二阶导数连续且存在的前提,但无法对系统方程与逻辑环节进行同步求解,这也是算法的局限性所在。

2.2 算法的计算效率分析

在提高算法收敛性的同时,还需要考虑算法是否会引入额外的计算量,从而导致时域计算的效率降低。因此,需要对比引入斯蒂芬逊迭代前后交替求解法的计算量差异。由于计算机乘除运算耗时远大于加减运算,算法计算量仅统计乘除运算次数。

引入斯蒂芬逊迭代后,算法的计算量差异体现在以下两方面:1）根据式（6）构造A、D矩阵造成的计算量增加；2）各算法由于迭代公式的不同,导致进行状态变量与代数变量求解存在计算量差异。

对于方面1）,由于仿真过程中A、D矩阵各元素表达式差异较大,难以统计每个元素的计算量,只能对构造A、D矩阵的整体计算量进行评估。本文所提算法采用VDHN 法在各时步、各轮迭代间传递雅可比矩阵A,仅在收敛性较差时更新雅可比矩阵A。同时,采用虚拟导纳法,用D矩阵的常数部分Y+Yg近似D矩阵。因此,仿真过程中仅需要初始时刻以及拓扑变化的时刻重新构造D矩阵。若记仿真全过程A、D矩阵更新次数分别为nA、nD,单次更新A、D矩阵的计算量分别为OA、OD,则构造A、D矩阵的计算量C为:

由于采用了VDHN 法,nA的值实际上较小［27］,由于D矩阵的定常特性,nD的值也较小。因此,仿真全过程中构造A、D矩阵引入的额外计算量并不是影响仿真过程计算效率的主要原因。

对于方面2）,设差分方程和网络方程的阶数分别为n、m。记单次迭代中常规状态变量迭代与代数变量迭代的计算量为O1、O2。由式（19）可知,单次斯蒂芬逊迭代的计算包含1 次乘法操作和1 次除法操作。因此,对于n阶差分方程和m阶网络方程,各需对n个状态变量和m个代数变量进行斯蒂芬逊迭代,计算量分别为2n和2m。假设某时步共需进行K次迭代,则常规迭代与所提算法在求解差分方程与代数方程上的计算量对比如表1 所示。

表1 常规迭代与斯蒂芬逊迭代计算量差异Table 1 Difference in calculation overhead between regular iterations and Stephenson iterations

根据表1 可知,采用常规迭代格式与斯蒂芬逊迭代格式时,计算量的差异与O1、O2的具体表达式相关,而O1、O2的表达式则与实际计算中矩阵A与矩阵D的取值有关。需要作进一步分析:

1）若采用式（3）的原始交替求解法,即取A=I、D=Y,对单个差分方程的求解涉及1 次乘法操作,故O1等于状态变量的阶数n；而代数方程的求解则涉及m阶导纳矩阵的求逆,故O2为kmm3,其中,m3为矩阵求逆的计算复杂度,而km为考虑导纳矩阵稀疏度所取系数。此时,常规迭代与斯蒂芬逊迭代中,差分方程计算量表达式均为n的一次表达式,但采用斯蒂芬逊迭代时一次项系数稍大；网络方程计算量表达式均为m的三次表达式,但斯蒂芬逊迭代的三次项系数稍小。

2）若采用式（9）的迭代格式,引入完整矩阵A与近似矩阵D,则差分方程与网络方程的求解计算量体现在对矩阵A、D的求逆上。因此,O1、O2分别为kAn3、kDm3,其中,kA、kD分别为考虑A、D矩阵稀疏度所取系数。此时,差分方程与网络方程计算量表达式均分别为n与m的三次表达式,但斯蒂芬逊迭代的三次项系数稍小。

从上述两方面分析可知,由于采用了VDHN法,仿真过程中构造A、D矩阵引入的计算量较小；对于迭代格式不同带来的计算量差异,仅在常规迭代格式采用原始交替求解法时,所提算法在差分方程求解的计算量上略高于常规迭代方法,而在其他迭代格式下所提算法均没有引入额外的计算量。

此外,算法的计算效率是单次迭代计算量与迭代次数的综合结果。即使原始交替求解法的单次迭代计算量低于斯蒂芬逊迭代,仍可能因为迭代次数过高,而使总体计算效率低于基于斯蒂芬逊迭代的改进交替求解法。

3 算例分析

3.1 算法正确性验证

在IEEE 标准16 机68 节点系统进行算法的正确性验证。系统包含16 台7 阶同步发电机,11 台IEEE-DC4B 型 励 磁 机,1 台IEEE-ST1A 型 励 磁 机,12 台电力系统稳定器,动态元件最小时间常数为0.01 s,雅可比矩阵A规模为227 阶,网络导纳矩阵为68 阶复数矩阵。测试电脑CPU 配置为2.3 GHz Xeon 5218,256 GB 内存,操作系统为CentOS 7.5.1804。

案例测试中涉及的时域计算算法如表2 所示。表中:各算法在代数方程迭代格式中,D矩阵统一取D=Y+Yg。

表2 算例涉及的算法Table 2 Algorithms involved in case study

考虑到原始交替求解法,即表2 中算法1 存在最大步长限制,无法在0.010 s 的步长下取得收敛,在进行正确性验证时,算法1 采用0.005 s 固定步长进行仿真,其余算法采用0.010 s 固定步长进行仿真。扰动设置为1.0 s 时刻,220 kV 3 号母线发生三相短路故障,t=1.1 s 时故障清除。仿真时长为20 s,观察变量为发电机G2、G4、G6、G8、G10、G12、和G16 的功角差。

G2 与G16 的功角差曲线如图2 所示,其余发电机的功角差曲线见附录B 图B1。从图中可以看出,采用不同算法进行时域仿真得到的结果基本一致。

图2 采用不同算法时的时域曲线Fig.2 Time-domain curves by using different algorithms

考虑到原始交替求解法的仿真固定步长小于其余4 种算法,后续算例中将不再对原始交替求解法进行讨论。

3.2 算法收敛性提升效果验证

为验证算法在含新能源场景下也能提高时域计算的收敛性与计算效率,设置68 节点系统的新能源场 景 为:将 系 统 中1 号、2 号、5 号、7 号、8 号 以 及10 号母线上的同步发电机替换为相同容量的双馈风机,双馈风机模型及参数与MATLAB2018b/Simulink 中双馈风机相量模型相同。

针对无新能源场景和含新能源场景,分别对每个算法重复进行10 次仿真,并对计算耗时求平均值。统计两种场景下各算法的总迭代次数及耗时结果如表3 所示。

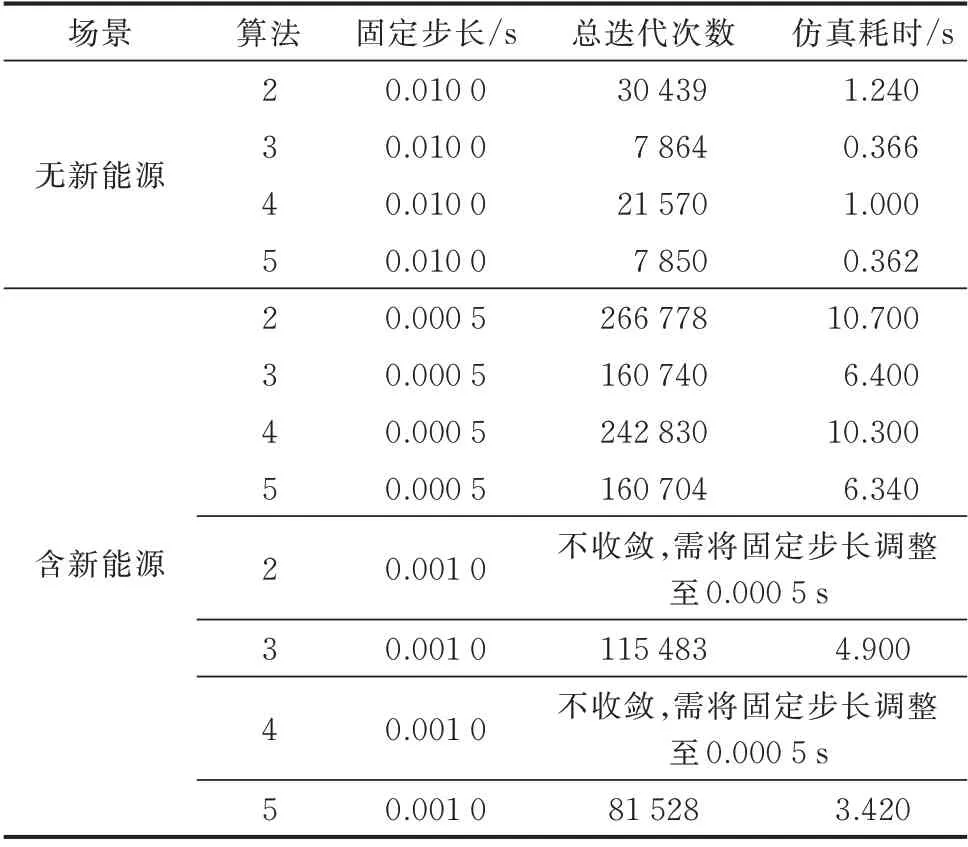
表3 采用不同算法时的总迭代次数与耗时对比Table 3 Comparison of total number of iterations and time consumption when using different algorithms

从表3 可以看出,不论是无新能源场景还是含新能源场景,在矩阵A格式相同的情况下,引入斯蒂芬逊迭代均可有效改善暂态时域仿真的迭代过程。在无新能源场景中:算法3 的仿真耗时相对算法2 减少70.5%；算法5 的仿真耗时相对算法4 减少63.8%；算法5 的仿真耗时相对算法2 减少70.8%。在含新能源场景中:算法3 的仿真耗时相对算法2减少40.2%；算法5 的仿真耗时相对算法4 减少38.4%；算法5 的仿真耗时相对算法2 减少40.7%。

结合2.3 节算法的计算效率分析可知,虽然算法3 的单次迭代计算量略高于算法2,但由于引入斯蒂芬逊迭代后计算过程的收敛性得到了较大改善,总的迭代次数远低于算法2。因此,在计算效率方面,算法3 相较算法2 取得了巨大的优势。同样的分析也适用于算法4 与算法5。

此外,表3 中还给出了新能源场景下,固定步长为0.001 s 时算法2 至算法5 的性能对比。此时,算法2 和算法4 无法在0.001 s 的固定步长下收敛,而算法3 和算法5 则仍能在0.001 s 的固定步长下收敛。这说明在新能源场景下,引入斯蒂芬逊迭代后,时域计算对新能源接入带来的刚性有更好的适应性。同时,从迭代次数与仿真耗时来看,算法5 的收敛性优于算法3,说明引入完整的矩阵A对于提高时域计算的收敛性是有益的。

图3 给出了含新能源场景下20 s 仿真过程中,4 种算法每一时步的迭代次数比较。

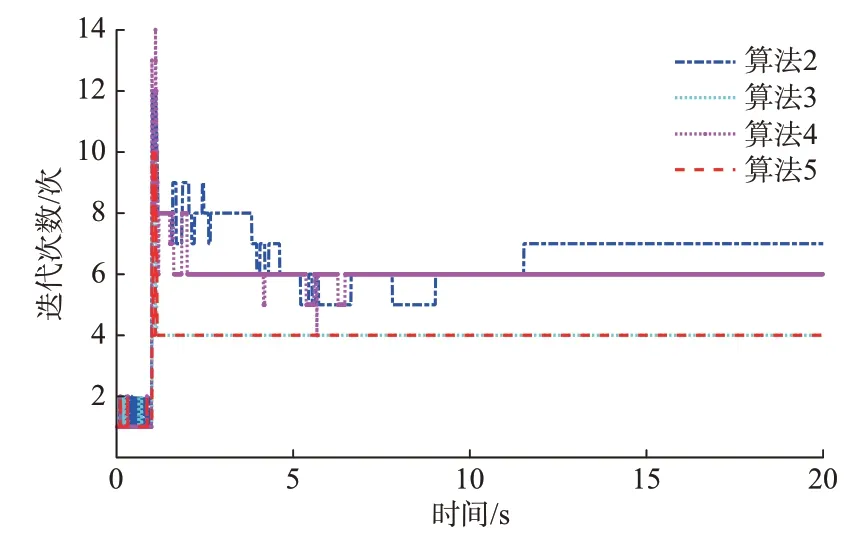
图3 采用不同算法时的迭代次数曲线Fig.3 Curves of iteration numbers when using different algorithms

从图3 中可以看出,在仿真初期,4 种算法都可以在较低的迭代次数内完成本时步的计算。当1.0 s 发生短路故障后,4 种算法的迭代次数都出现明显的提升,但算法3 和算法5 的迭代次数增长幅度明显低于算法2 和算法4,且算法3 和算法5 在1.5 s左右稳定于每时步进行4 次迭代,而算法2 与算法4则在暂态后一直保持较高的迭代次数。

3.3 实际电网下的算法效果验证

在某2 970 节点区域电网验证本文所提算法对大型电力系统仿真的有效性。系统包含2 970 条母线、1 613 条线路、254 台同步发电机与12 台双馈风机,包含励磁、调速共16 种模型,负荷采用恒定阻抗+感应电机模型,雅可比矩阵A规模为9 354 阶,网络导纳矩阵规模为2 970 阶,扰动设置为t=1.0 s某500 kV 母线三相短路故障,t=1.1 s 故障清除。

图4 展示了采用本文算法以及BPA 进行仿真时,故障母线处发电机的功角差曲线。其他变量的对比见附录B 图B2。可以看出,本文算法的仿真结果与BPA 的仿真结果具有一致性。

图4 本文算法与BPA 时域曲线对比Fig.4 Comparison of time-domain curves by the proposed method in and BPA

采用表2 中的算法2、3、4 重复进行10 次10 s 的时域仿真,统计各算法的总迭代次数以及耗时结果如表4 所示。

表4 新能源场景下采用不同算法时的总迭代次数与耗时对比Table 4 Comparison of total iteration numbers and time consumption when using different algorithms in renewable energy scenarios

从表4 可以看出,在大电网仿真中,算法2 与算法4 无法在较大步长条件下进行仿真,需要将步长调整至10-6数量级,无法满足机电暂态仿真的需要,而算法3 和算法5 则仍能以0.001 s 的固定步长进行仿真。这说明引入斯蒂芬逊迭代对于时域计算收敛性提升及系统强刚性的适应性。

4 结语

本文从不动点迭代的理论出发,分析交替求解法的迭代求解过程,揭示了交替求解法不收敛的机理,提出了基于斯蒂芬逊迭代的电力系统时域计算交替求解法。通过算例分析得到以下结论:

1）对于刚性电力系统,由于系统存在较小时间常数的动态环节,传统交替求解法及其改进算法都将面临微分方程强刚性带来的收敛性问题。

2）引入斯蒂芬逊迭代能够有效改善交替求解法对于系统刚性的适应性,能够采用比原始交替求解法更大的步长对系统进行定步长仿真。

3）通过引入差分方程与代数方程的雅可比矩阵A、D,能够较好地改善系统的收敛性,配合斯蒂芬逊迭代则能够最大限度地兼顾交替求解过程的收敛性与效率。

4）在IEEE 标准68 节点系统中,同时引入矩阵A、D并采用斯蒂芬逊迭代进行时域计算,在无新能源和有新能源接入的情况下,相比于原始交替求解法,仿真耗时分别减少70.8%和40.7%。在2 970 节点实际电网中,引入斯蒂芬逊迭代也能够改善时域计算的收敛性,适应系统的强刚性。

未来将进一步研究非线性方程求解领域的其他高阶迭代方法在时域计算中的适用性。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。